支持多跳的格上属性基同态代理重加密方案
王依然,陈燕俐,王慧婷
(南京邮电大学 计算机学院, 江苏 南京 210023)
作为一种新型计算模式,云计算能够为海量终端用户提供可靠的、动态的计算环境。 远端用户对云资源进行访问时,如何保护敏感数据的机密性和安全共享,是云计算和云存储安全研究的重要方向。对存储在云服务器的共享信息进行加密可以很好地解决云服务提供商(Cloud Service Provider,CSP)不完全可信场景下数据的机密性问题。 但这也造成了云计算环境中存在着大量用户共享密文数据需要进行密文转换的场景,而如果由不完全可信的CSP 在云端进行解密又重新加密处理,就会产生用户数据泄露的风险,而代理重加密(Proxy Re-Encryption,PRE)方案可安全可靠地实现云环境下数据的共享和访问。 代理重加密概念由Blaze 等[1]首次提出,允许一个半可信的代理服务器(Proxy Servers,PS)把用授权人(Delegator)Alice 的公钥加密的密文转换成用被授权人(Delegatee)Bob 的公钥来加密的密文。 同时,此代理服务器对于该密文所对应的明文一无所知。 代理重加密方案根据密文的转换次数,可以分为单跳(Single-hop)和多跳(Multi-hop),单跳的代理重加密方案只允许密文被转换一次,多跳则可以被转换多次。 代理重加密方案目前已在多个领域中得到了成功应用,如云计算访问控制、加密电子邮件转发、分布式文件系统的安全管理和垃圾邮件过滤等。
通常代理重加密的通信模型是一对一,即一个授权人对应者一个被授权人,这限制了重加密方案在很多一对多或者多对多实际场景的应用。 属性基代理重加密(Attribute-based Proxy Re-encryption,ABPRE)[2]结合了代理重加密和属性基加密[3]的概念,允许半可信代理将特定访问策略或属性集合下的密文转换为另一个访问策略下的密文,且无需透漏任何关于明文的信息,使得代理重加密更加灵活、方便和高效,更好地实现了云环境下多对多的细粒度数据共享。 随着近年来量子计算机研究取得突飞猛进的进展[4],由于可有效抵抗量子攻击、且计算简单、高效,格上的代理重加密算法以及属性基代理重加密算法陆续被提出。 但目前的属性基代理重加密虽然能实现在云端密文的代理,但却无法实现密文的同态运算,包括新鲜密文和重加密密文之间的运算和处理。
全同态加密(Fully Homomorphic Encryption,FHE)不仅可满足传统加密的功能,并可在不知道密钥的情况下,对密文进行任意计算。 针对目前格上属性基代理重加密方案不能实现密文同态运算的问题,受文献[5]同态代理重加密思想的启发,在Brakerski 等[6]提出的目标同态属性基加密方案(Target HABE,T-HABE)基础上,首次提出一种多跳的格上属性基同态代理重加密方案(Attributedbased Homomorphic Proxy Re-encryption,ABHPRE),在实现属性基代理重加密的基础上,实现了密文的全同态运算。 主要贡献如下:
(1) 方案属性加密基于KP-ABE,根据属性集合x对消息进行加密,并根据基于布尔电路的访问策略f生成密钥。 只有当f(x)=0 时,密文才能通过密钥解密。 允许半可信代理将满足某访问策略的密文转换为另一个访问策略下的密文,很好地实现了云环境下多对多的细粒度数据共享。
(2) 方案新鲜密文和重加密密文格式相同,可实现单向多跳的密文代理重加密。 此外方案安全性高,可抵抗诚实重加密攻击(Honest Re-encryption Attacks,HRA),即使恶意被授权人和半诚实代理人联手得到重加密密文对应的输入密文,也无法获取授权人的私钥。
(3) 将属性基同态加密与代理重加密相结合,实现了对新鲜密文和重加密密文的全同态运算,包括同态加法、同态乘法和与非运算。
1 相关工作
1.1 代理重加密
自从Blaze 等[1]于1998 年提出代理重加密以来,已经有越来越多的代理重加密方案提出,如基于EIGamal 的、基于EIGamal 和RSA 的以及基于双线性对等。 2010 年,Xagawa 等[7]提出一个格上基于LWE 假设构造代理重加密方案,但方案是双向的,并且不抗同谋。 2013 年,Aono 等[8]在文献[9]公钥加密方案基础上,利用同态加密中密钥转换技术,提出了第一个基于LWE 假设的格上单向多跳代理重加密方案,在标准模型下选择明文安全(CPA)性,但该方案只能实现弱密钥隐私。 2014 年,Kirshanova 等[10]对陷门定义进行扩展,提出一个在选择模型中选择密文安全(CCA)的,同样基于LWE假设的单向代理重加密方案,但该方案不能实现密钥隐私。 2015 年,Nishimaki 等[11]分别基于Regev公钥加密方案[12]和Lindner[9]公钥加密方案提出两个基于LWE 假设的密钥隐私PRE 方案,方案通过对被授权人公钥进行随机化的方式对授权人匿名,从而实现密钥隐私安全,该方案缺点是只具备单跳性质。 2016 年,Ma 等[5]提出一个同态代理重加密方案,即原始密文和重加密密文都可以实现同态运算。 2019 年,Fan 等[13]指出了文献[1]方案存在的安全性问题,提出一个改进的CCA 安全的代理重加密方案。 2021 年,Singh 等[14]构造了一个可实现主密钥安全(Master Secret Security)的单向代理重加密方案, 即不诚实的代理和恶意被授权人不能共谋计算出授权人的密钥。
1.2 属性基代理重加密
与属性基加密方案相同,属性基代理重加密分为两种类型:密钥策略属性基代理重加密(Keypolicy Attribute-based Proxy Re-encryption, KPABPRE)和密文策略属性基代理重加密(Ciphertextpolicy Attribute-based Proxy Re-encryption, CPABPRE)。 KP-ABRE 的密钥和访问结构相关,密文和属性集合相关,代理重加密是将某访问结构可以解密的密文转换为另一个访问结构下可解密的密文。 CP-ABPRE 的密文和访问结构相关,密钥和属性集合相关,代理重加密是将某访问结构下加密的密文转换为另一个访问结构下的密文。 2009 年,Liang 等[2]提出了第一个CP-ABPRE 方案,访问策略采用基于正负属性组成的与门结构,方案满足选择CPA 安全。 随后,Liang 等[15]提出了一个满足适应性CCA 安全的CP-ABPRE 方案。 2016 年,Ge等[16]构造了第一个可证CPA 安全的KP-ABPRE 方案。 但上述ABPRE 方案都是基于双线性对,无法抵御量子攻击。 2019 年,Li 等[17]提出第一个格上的单跳单向CP-ABPRE 方案,访问策略基于正负属性组成的与门结构,方案采用陷门采样技术生成重加密密钥,但必须输入主密钥作为参数,因此存在主密钥泄露的安全性问题。 2021 年,Luo 等[18]构造了第一个多跳的KP-ABPRE 方案,方案支持多项式深度策略电路,具有较短的私钥,密钥的大小取决于支持的策略电路的深度,但该方案的私钥是一个扩展矩阵的陷门,在解密时必须通过采样函数重新生成私钥,并且该方案只能实现CPA 安全。 2021 年,Susilo 等[19]提出了一个标准模型下可抵抗诚实重加密攻击(Honest Re-encryption Attacks,HRA)的单跳KP-ABPRE 方案,方案通过密钥转换技术生成重加密密钥,克服了CPA 安全模型中可能存在的被授权人在得到重加密消息的密文情况下泄露授权人私钥的安全问题,但不能实现密文的同态。
2 预备知识
2.1 符号
本文用R 表示自然数集,用Z 表示整数集。Zq表示(- q/2,q/2] 中的整数。 对于任何正整数d >0,[d] 表示{1,2,…,d}。 用「⏋表示向上取整。 设S是一个集合,P是S上的概率分布。a←S表示a∈S从S中随机均匀采样,b←P表示b∈S从P中采样。 向量x的第i个元素由xi表示。‖x‖∞表示向量x的l∞范数(最大范数)。<x,y >表示两个向量的内积。 矩阵X的第i列向量由X[i] 表示。对于矩阵X∈Rm×n,X的l∞范数定义为‖X‖∞=maxi∈[n]{‖X[i]‖∞},XT表示X的转置。 对于两个矩 阵表示矩阵A和B串联生成的矩阵。In表示n × n维单位矩阵,0n×m表示所有项都为0 的n × m维矩阵。 符号negl(λ) 表示λ∈N 的可忽略函数集。 本文依赖于有界域上支持的分布,如果整数集Z 上的分布χ仅支持分布在[- B,B] 上,则称χ为B有界分布[6]。
2.2 LWE 问题
误差学习(Learning With Errors, LWE)问题由Regev[12]提出,已经被证明为一个难解的多项式复杂程度的非确定性(Non-deterministic Polynomial,NP)问题。
定义1判定性LWE(Decisional LWE,DLWE)问题。 设安全参数λ,参数n =n(λ),q =q(λ) ≥2为整数模数,χ =χ(λ) 为Z 上的高斯分布。D0=χ。 DLWE 问题就是上述两个分布:D0、D1不可区分。
2.3 Gadget 矩阵和位分解
对于任意模数q,l =「lgq⏋, 行向量g =(20,Gadget 矩 阵Gn =In⊗g∈
函数g-1:Zq→Zl,表示将一个数分解为二进制数,对于任意a∈Zq,列向量x =g-1(a) 是{0,1}向量,并且有< g,x >=a。 符号表示对矩阵A的每个元素进行二进制分解,得到行扩张的矩阵,有G·G-1(A)=A。
2.4 格陷门和离散高斯分布
定理1陷门生成算法TrapGen(1n,1m,q) →(A,TA)[20]。 存在一个概率多项式随机算法,当m =Θ(nlgq),输出一对使得A统计接近均匀分布且TA是的一个短基,且
定理2右扩展算法ExtendRight(A,TA,B) →TA‖B[20]。 给定矩阵的一个基TA,算法输出格的一个短基T[A‖B],其中,‖TA‖GS =‖TA‖B‖GS。
定理3左扩展 算法ExtendLeft(A,G,TG,S) →TA‖B[20]。 给定矩阵,格Λ⊥(G)的一个短基TG, 随机矩阵S∈Zm×mq算法输出格的 一 个 短 基T[A‖G+AS], 其 中,‖T[A‖G+AS]‖GS≤‖TG‖GS·(1+‖S‖2)。
引理1预采样算法[20]。SamplePre(A,TA,u,σ)→e:给定一个矩阵的一个基TA,一个向量和一个高斯参数σ,算法输出一个采样于分布的向量e。
2.5 HABE 同态运算函数
定义2[6]令n,q,l∈N,N =n「lgq⏋,B1,…,假设访问策略f∈{0,1}l→{0,1} 的电路深度为d,且只包含与非门电路。 将B1,…,Bl接入电路的线路端口,对f中每个线路端w,u,v为其的左右输入,定义Bw =G -Bu G-1(Bv),则可以递归得到矩阵Bf,算法表示为
推论1[6]则存在一个多项式时间的算法EvRelation, 令H =那么有另外,如果则有计算则有Bf =ARf +f(x)G。
2.6 KP-ABHPRE 形式化定义和安全模型
令访问策略集F ={f:{0,1}l→{0,1}},消息空间M,一个密钥策略的属性基同态代理重加密(KP-ABHPRE) 方 案 由 算 法Setup、KenGen、Enc、Dec、Eval、ReKeyGen和ReEnc组成,具体描述如下。
(1)Setup(1λ,l) →(PP,msk):输入安全参数λ、属性数量l,输出公共参数PP、主密钥msk。
(2)KenGen(PP,msk,f) →skf: 输入公共参数PP、主密钥msk和访问策略f∈F,输出私钥skf。
(3)Enc(PP,x,μ) →c:输入公共参数PP、消息μ∈M和属性x∈{0,1}l,输出密文c。
(4)Dec(PP,skf,c) →μ:输入密钥skf、属性x加密下的密文c,如果f(x)=0,输出消息μ;否则,输出⊥。
(5)ReKeyGen(PP,skfi,fj) →rk(i→j):输入公共参数PP、访问策略fj和访问策略fi私钥skfi, 输出重加密密钥rk(i→j), 该密钥可将属性x(i)加密下的密文 重 加 密 为 属 性x(j)加 密 下 的 密 文, 满 足fj(x(j))=0。
(6)ReEnc(PP,rk(i→j),fi,ct(i)) →ct(j):输入公共参数PP、重加密密钥rk(i→j)、 访问策略fi、 属性x(i)加密下的密文ct(i)和重加密密钥rk(i→j), 如果fi(x(i))=0, 输出属性x(j)加密下的重加密密文ct(j),否则,输出⊥。
(7)Eval(PP,f,g,(ct1,…,ctn)) →ct∗: 输入公共参数PP、目标访问策略f、 同态运算电路g和符合访问策略f的密文ct1,…,ctn,输出同态运算密文ct∗。
定义3KP-ABHPRE 正确性。 一个密钥策略的属性基同态代理重加密(KP-ABHPRE) 方案(Setup,KenGen,Enc,Dec,Eval,ReKeyGen,ReEnc)可正确解密得到消息μ∈M,如果满足:
(1) 对于任意的(PP,msk) ←Setup(1λ,l),任意的f∈F, 任意消息μ∈M和任意属性x∈{0,1}l,如果f(x)=0, 则有Dec(PP,skf,Enc(PP,x,μ))=μ。
(2) 对于任意rk(i→j)←ReKeyGen(PP,skfi,fj),任意的ct(i)←Enc(PP,x(i),μ),如果fj(x(j))=0,则Dec(PP,skfj,ct(j))=μ, 其 中,ct(j)←ReEnc(PP,rk(i→j),fi,ct(i)),并且fi(x(i))=0。
(3) 对于任意λ,任意μ1,…,μn∈M,有g(μ1,…,μn)=Dec(skf,(Eval(PP,f,g,ct1,…,ctn)))。
定义4如果对于多项式时间的攻击者在如下游戏中的优势是可忽略的,那么KP-ABHPRE 方案在诚实重加密攻击下是不可区分(IND-HRA)安全的。
(1) 初始化。 攻击者A发送目标属性集x∗给挑战者。
(2) 设 置。 挑 战 者 运 行Setup(1λ,l), 获 得(PP,msk),并将公共参数PP发送给A。 挑战者引入一个计数器Count,初始为0;一个存储键值的集合H,初始为空;一个集合Set,初始为空。
(3) 查询阶段1。 攻击者A可以任意多项式次地对以下预言进行查询。
-OKeyGen:输入策略f∈F,当f(x∗)=0 时,随机预言机输出⊥,否则,输出策略f下的私钥skf←KeyGen(PP,msk,f)。
-OReKeyGen:输入两个策略fi和fj,当fi(x∗)=0,fj(x∗) ≠0 时,随机预言机输出⊥,否则,输出重加密密钥rkf→g←ReKeyGen(PP,skfi,fj)。
- OEnc:输入属性集x和消息μ,随机预言机输出密文c←Enc(PP,x∈{0,1}l,μ)。Count值加1,并将键(x,Count) 和密文c添加到集合H中。
- OReEnc:输 入 策略fi, 键(x,k), 其 中k≤Count,如果H中没有与键(x,k) 对应的值,随机预言机输出⊥,否则,让c作为H中对应的值。 如果fi(x) ≠0,输出⊥代表c是无效的,否则,输出重加密密文ct(j)←ReEnc(PP,rkf→g,c)。
(4) 挑战。 攻击者A在属性集x∗下提交两个消息μ0,μ1∈M给挑战者。 挑战者通过选择一个随机比特b∈{0,1}, 输出一个挑战密文Enc(PP,x∗,μ)。Count值加1,并将Count添加到集合Set中。 将值及对应的键(x∗,Count) 添加到H中。
(5) 查询阶段2。 在接收到挑战密文后,攻击者A仍有权限访问查询阶段1 中的OKeyGen,OReKeyGen,OEnc和OReEnc, 除了OReEnc中的以下 约束:如 果fj(x∗) ≠0 ∧k∈Set,输出⊥。
(6) 猜测。 在A输入b′,如果b =b′,随机预言机输出1,否则,输出0。
在游戏中,攻击者A的优势定义为Adv(λ)=|Pr[b′ - b]-1/2|,如果对于任何多项式时间里的攻击者,有Adv(λ)=negl(λ),则认为方案是诚实重加密攻击下的不可区分安全的。
3 密钥策略的属性基同态代理重加密方案KP-ABHPRE
设访问策略集Fl,dF ={f:{0,1}l→{0,1}},其中,l、dF分别为属性数以及访问策略电路的最大深度;消息空间为M。 KP-ABHPR 方案由算法Setup、KenGen、Enc、Dec、Eval、ReKeyGen和ReEnc组成,具体构造如下。
(1)Setup(1λ,1l)
选取DLWE 参数n、q、B、χ和m,有n≥λ,q≤2n,lq =「lgq⏋,N =nlq,m =Θ(nlq),M =(m +N +1)lq,χ =χ(n) 为B有界的错误分布。 进行如下操作:
①生成矩阵陷门对(Α,TA) ←TrapGen(1n,1m,q),其中,
(2)Keygen(PP,msk,f)
①给定一个{0,1}l→{0,1} 的访问策略电路f,按照2.5 节计算
②使 用 右 扩 展 函 数 生 成 陷 门T[A‖Β0+Βf]←ExtendRight(A,TA,Β0+Βf),再使用采样函数生成rf←SamplePre([A‖Β0+Βf],T[A‖Β0+Βf],v,σ),令私 钥skf =[- rf‖1], 可 以 看 出skf·[Α‖Β0+Βf‖v]T=0T。
③输出私钥skf。
(3)Enc(PP,x∈{0,1}l,μ∈{0,1})
②计算
③对于每个属性xk,k∈[l], 计算Ck =
(4)ReKeyGen(PP,skfi,fi,ct(i))
①选取一个满足fj(x(j))=0 的属性集x(j)=
⑤输 出 重 加 密 密 钥rk(i→j)=(x(j),Μ(i→j),N(i→j))。
(5)ReEnc(PP,rk(i→j),fi,ct(i))
①调用子函数Cfi←ApplyF(ct(i),fi), 将属性加密x(i)下的密文ct(i)转换为对应的访问策略fi加密下的密文其中,为Cfi的前(m +N)lq列,为Cfi的最后lq列。
② 计 算 并 输 出C(j)= M(i→j)(I(m+N+1)⊗
(6)Dec(PP,skf,ct)
①将属性加密x下的密文转换为对应的访问策略f加密下的密文,ctf←ApplyF(ct,f)。
②计算c =skfctf =[- rf‖1]Cf。 令uT=计算如果则μ =0,否则,μ =1。
(7)ApplyF(ct,f)
该函数是辅助子函数,功能是对密文ct =(x,根据f∈F进行如下同态运算:
③输出密文ctf =Cf。
(8)Eval(PP,f,g,(ct(1),…,ct(n)))
对 每 一 个i∈ [n], 计 算ApplyF(ct(i),f) ,计算并输出同态运算密文ct∗=
4 方案分析
4.1 正确性分析
证明:下面根据密文的类型分两种情况证明。
ApplyF(ct(i),fi) →Cfi =([A‖(B0+Bfi)‖v]TS +E +μGm+N+1)
c =skfiCfi =[- rfi‖1]([A‖(B0+Bfi)‖v]T·S +E +μGm+N+1)=μ[- rfi‖1]G +[- rfi‖1]E
误差:
因 此, 当 且 仅 当 误 差 ‖e‖=时,新鲜密文可以正确解密。
由于:
又因为:
4.2 同态性分析
从4.1 分析中可以看到原始密文和重加密密文表达式相同,设
其中,误差=[- rf‖1](E1+E1)。
其中, 误 差=μ1[- rf‖1]E2+[- rf‖1] ·
其中, 误差=μ1[- rf‖1]E2+[- rf‖1]·
综上所述,KP-ABHPRE 方案密文满足同态性。
4.3 安全性证明
定理5 KP-ABHPRE 方案在DLWE 假设下是IND-HRA 安全的。
证明:方案的密文CPA 安全证明和文献[1]相同,是在一系列游戏中进行的,故此省略。 下面只给出HRA 安全的证明。
(1)Sim.Setup(1λ,l)
(2)Sim.KeyGen(PP,f∈F,f(x∗) ≠0)
③ 使用左扩展函数生成陷门T←再使用采样函数rf←SamplePre([A‖B0+Bf],T,v,σ) →e,生成 私 钥skf =[- rf‖1], 可 以 看 出,skf·[Α‖Β0+Βf‖v]T=0T。
(3)Sim.ReKeyGen(PP,fi,fj∈F,fi(x∗)=0)
对于fi(x∗)=0, 如果fj(x∗) ≠0, 输出⊥;否则,选取随机矩阵
输 出 重 加 密 密 钥rk(f→g)=(x∗,M(i→j),N(i→j))。
(4)Sim.ReEnc1(PP,ct(i)(x =x∗),fi,fj∈F)
如果f(x∗) ≠0,输出⊥,否则:
①选取一个满足fj(x(j))=0 的属性集x(j)=选 择 随 机矩 阵S(i→j), 误 差 矩 阵以及误差向量,对每一个a∈[0,1,…,l],b∈[(m +(l +1)N +1)lq],采样1}m×N, 计 算 误 差 矩 阵计 算 并 输 出
②将ct(i)表示为
(5)Sim.ReEnc2(PP,ct(x≠x∗),fi,fj∈F,f(x∗)=0)
如果f(x) ≠0,输出⊥。 否则,对于f(x)=0,执行以下操作:
①因为x≠x∗,至少存在一个i∈{1,…,l},使得不失一般性,假设0。 因为的陷门,因此,首先计算然 后 用ExtendRight算 法 计 算F =[A‖xlG +Bl‖B0‖x1G +B1…‖xl-1G +Bl-1‖v]陷门TF =ExtendRight(Α‖xlG +Bl,T(Α|xlG+Bl),[B0‖x1G +B1‖…‖xl-1G +Bl-1‖v]),通过行交换得到F′ =[A‖B0‖v‖x1G +B‖…‖xlG +Bl]的 陷 门TF′。 最 后 通 过 采 样 函 数rf←SamplePre(F′,TF′,v,σ) →e。
②选 取 一 个 满 足fj(x(j))=0 属 性 集x(j)=选择随机矩 阵S(i→j), 误差矩阵以及误差向量,对每一个a∈[0,1,…,l],b∈[(m +(l +1)N +1)lq],采样1}m×N, 计 算 误 差 矩 阵计 算并输出
③将ct(i)表示为
④计 算 并 输 出C(j)=M(i→j)·(Im+N+1)⊗
Sim.ReEn1或Sim.ReEn2模拟生成的重加密密文需要正确解密。 对于模拟生成的重加密密文的正确性,当fj(x(j))=0 时,对重加密密文进行运算得到分布中采样的,有因此现在令计算通过选择参数,可正确解密模拟重加密密文。
综上所述证明成立。
4.4 性能分析
首先对本文ABHPRE 方案与文献[17-19]的属性基代理重加密方案进行性能比较。 如表1 所示,文献[17]方案是基于CP-ABE,访问策略采用与门结构,访问策略不够灵活。 文献[18]构造了第一个多跳的KP-ABPRE 方案,但该方案只能实现CPA安全。 文献[19]可实现HRA,但只能实现单跳,并且同样不能实现密文同态运算。 而本文提出的ABHPRE 方案不仅可以实现单向多跳、满足HRA安全,而且可以实现密文同态运算。
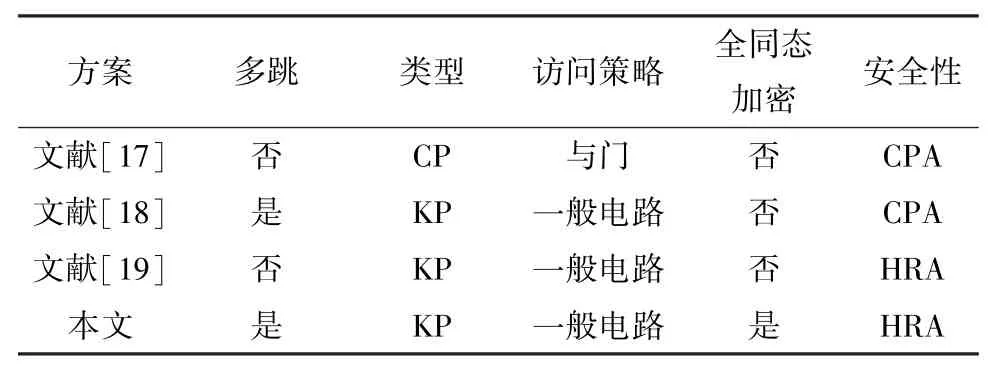
表1 方案性能比较
从公钥大小、主私钥大小、私钥大小、重加密密钥大小、密文大小和重加密密文大小等方面,将本文方案与文献[19]方案进行比较,比较结果如表2 所示。 可以看到本文方案私钥较小,但由于本文方案满足多跳功能,并且可实现同态运算,因此密文是矩阵形式,长度大于文献[19]方案。

表2 方案的密文密钥大小比较
5 结束语
本文提出一种格上的可抵抗HRA 攻击的属性基同态多跳代理重加密方案。 方案代理重加密是基于密钥策略的,允许半可信代理将符合特定访问策略的的密文转换为符合另一个访问策略下的密文。与以往方案相比,本文方案不仅可以实现单向多跳,并对密文进行多次重加密,还实现了对新鲜密文和重加密密文的全同态运算。 但目前方案还只能实现相同策略的密文同态运算,下一步工作要提出可实现不同访问策略密文同态运算的格上属性基同态代理重加密方案,进一步提高访问控制的灵活性。

