基于机器学习储备池计算的混沌保密通信机制设计与实现
靳雷生,王 振,刘 卓,薛 瑞,蒋宗庆
(南京邮电大学 集成电路科学与工程学院,江苏 南京 210023)
混沌同步广泛应用于保密通信设计[1-6]。 传统的保密通信机制中,发送端基于非线性动力学系统产生混沌信号,进而对拟发送信号进行加密。 在接收端,除自适应同步外,须配备类型和参数一致的动力学系统,以实现与加密动力学系统的完全同步。此外,在发送端和接收端之间,往往需要设计一种复杂的耦合机制为同步实现提供必要条件[7]。 传统的混沌保密通信在以下两个方面仍需进一步改进[8-9]:(1) 在实际条件下,由于不可避免地制造误差,在发送端和接收端配置相同的动力学系统是难以实现的,而参数误差会导致同步质量降低;(2) 基于安全性考虑,用于发送端加密的混沌系统往往是需要实时可变的,这种情形下,接收端也必须做出相应改变,这样会涉及硬件的替换和重置,从而导致通信成本提高。 近几年,一种可用于预测非线性动力学系统演化行为的机器学习方法——储备池计算(Reservoir Computing,RC)[10-14]引起了众多研究者的兴趣。 例如,Lu 等[15]利用该算法,基于有限的并发系统状态测量,研究了动力学系统中的时变状态演化。 Appeltant 等[16]提出一种全新的RC 计算架构,该架构仅使用一个具有延迟反馈的非线性系统完成计算,解决了传统RC 算法对大量神经元需求的弊端。 Rafayelyan 等[17]提出一种可以在大型网络上进行储备池计算的光学方案,实现了大规模时空混沌预测。 实验上,储备池计算与MEMS 感算一体的可行性也得到了证明[18]。 最近,有关RC 与保密通信的交叉研究也引起了众多关注。 例如,2022年,钟东洲等[19]报道了一种基于光学储备池计算的保密通信方案,该方案利用光泵浦自旋VCSEL 两个非线性分量实现并行的延时类型RC,从而对发送端另一个携带有用信号的光泵浦自旋VCSE 进行预测、同步和解调;然而,该机制仅能用光泵浦自旋VCSEL 作为加密系统,并且尚未得到实验验证。2022 年,刘家跃等[20]报道了一种基于RC 的激光混沌同步保密通信方案,该工作在理论上验证了在通信接收端配备一个RC 实现对加密信息的同步与解调的可行性;然而,在实际工作中,接收端需要持续输入加密后的全部信息,一定程度上增加了被窃取的风险。 同年,Liu 等[21]进一步利用光纤对上述机制进行了混沌激光保密通信实验,验证了机制的实用性;但该机制是否可以适用于激光加密之外的保密通信应用,仍值得进一步研究。 2022 年,Tang等[22]提出了另一种基于RC 的混沌激光保密通信方案,然而该机制接收端需要配备两个RC,并且要求参数一致,这在实际实现过程中是很难达到的。因此,设计一种兼具灵活性、一般性和实用性于一体的基于RC 的保密通信方案,无论是对解决传统问题还是目前基于RC 的混沌同步保密通信都具有重要意义。
本文工作提出了一种新型的混沌保密通信机制。 通过在接收端中设计RC 算法模块,实现与发送端任意类型加密混沌系统的自适应同步,进而实现信息解密。 本方案中,接收端从一个被动终端转换为具有学习能力的“智能系统”,它经过训练后可以准确预测混沌加密系统的动力学轨迹,实现混沌完全同步。 数值研究方面,利用两种具有更高安全性的时滞混沌动力学系统[23-25]进行加密,以图像和语音作为保密传输内容,验证了方案的可行性。 实验方面,基于可编程逻辑芯片(FPGA),对该机制进行了硬件设计与实现,并以真实的视频传输为例,进一步证明了方案具有重要的实用价值。 本文工作对推动RC 在信息处理中的应用提供了重要参考价值,在一定程度上促进了保密通信技术与机器学习的交叉研究。
1 设计方法
1.1 混沌保密通信机制设计
本文所提出的混沌保密通信机制如图1 所示。该机制的创新之处在于利用一种先进的机器学习——RC 算法在处理混沌信号方面的优势,实现接收端的智能化。 新机制中,部署在接受端的RC经过少量数据训练后,可以对发送端加密系统的时间演化数据进行精确预测,从而实现与混沌加密信号的完全同步,进而在同步的过程中,将被加密的有用信息进行解调。 整个保密通信过程包含训练和预测两个阶段。
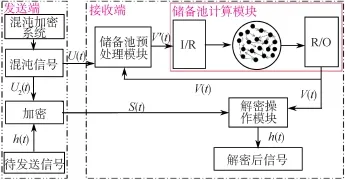
图1 基于机器学习-储备池计算的新型保密通信机制设计
下面对其工作过程进行阐述。 发送端中,h(t)为待传输的有用信号。 在发送前,首先由某种混沌加密系统生成信号U(t),并将U(t)划分为U1(t)和U2(t) 两个连续部分。 其中U1(t) 专门用于训练位于接收端中的RC,U2(t) 专门用来加密待发送信号h(t)。 下面的数值验证中,混沌信号U(t) 通过三维时滞洛伦兹(Time-delayed Lorenz, TDL)和一维麦基-格拉斯(Mackey-Glass, MG)产生。
RC 作为接收端的核心模块,由输入层、储备池和输出层组成。 其中,储备池含有N个随机连接的神经元。 储备池模块的动力学状态r(t),由式(1)描述[26]。
其中,Win和A分别为输入权值矩阵和邻接矩阵,α为定义在[0,1]范围内的泄漏率,偏置参数bin=1,V′(t)为储备池的输入信号(训练阶段V′(t)=U1(t))。储备池的输出信号定义为V(t),由储备池状态r和V′(t)共同决定,即
其中,Wout表示输出权重矩阵。 在训练阶段,需要训练出有效的Wout, 使储备池的输出为目标信号。例如, 在 实 际 通 信 时, 可 以 通 过 输 入 信 号U1(t)=[x(t1,t2,t3,…,tN),y(t1,t2,t3,…,tN),z(t1,t2,t3,…,tN)]T对RC 进行训练,目标信号设为V(t)=[x(t2,t3,t4,…,tN+1),y(t2,t3,t4,…,tN+1),z(t2,t3,t4,…,tN+1)]T。 然后,基于岭回归运算计算得出Wout
其中,I为单位阵,X为[bout,V′(t),r(t)] 组合矩阵,λ为偏置参数。 矩阵Y第m列是V(t)的第k -1列。Wout的求解是RC 训练的核心步骤,也是解密过程涉及的关键参数。
训练结束后,由于RC 配备了有效的Wout,它的输出可以实现与加密混沌信号U2(t)的完全同步。进入预测阶段后,接收端可以使用V(t),并利用减法操作解调信号S(t),从而得到有用信号h(t)。 然而,能够长时间地预测U2(t)是一个需要解决的问题。 由于混沌的初值敏感特性,建立的混沌同步难以长时间稳定[27]。 因此,在该通信机制中还需引入校准方法。 针对该问题,本文对不同类型加密系统引入了校准方法。 对于三维加密系统,例如TDL,V(t)作为储备池计算机的输出信号返回给输入时,需要将其中一个维度(非加密采用维度)替换为U2(t)中的对应维度向量;对于一维系统,例如MG系统,V(t)需要在反馈给输入一段时间后,使用真实值校准储备池计算的输入值。 通过引入上述方法,该保密通信机制可以实现长期稳定通信。
1.2 与传统保密通信机制比较
本文所提出的保密通信机制引入了新型机器学习算法——储备池计算,与传统混沌保密通信机制进行比较,所提出的机制有以下优点:第一,接收端不需要配置一个固定的动力学系统,可以与发送端采用的多种类型混沌加密系统实现完全同步,具有更高的灵活性与安全性。 第二,该机制不需要复杂的耦合机制设计,只需要通过训练来调整自身结构系数,以实现与加密混沌系统的智能化混沌同步。第三,该机制可以智能化适应发送端混沌加密系统中发生的变化。 通常在传统机制中,一旦混沌加密系统产生了改变,接收端也必须做出相应的改变,这可能涉及到硬件改变和安全性降低等问题,本文提出的方法可以实现智能化自适应同步,还可以有效提高安全性并降低成本。
2 数值研究
2.1 TDL 系统加密
本文首先采用TDL 系统作为混沌加密系统来验证所提保密通信机制的可行性。 TDL 的动力学方程[28]如下
其中,τ为系统的延时参数,a,b和c为系统可调参数。 为保证该系统处于混沌状态,首先计算了τ变化下的最大李亚普诺夫指数(Maximal Lyapunov Exponent, MLE),结果如图2 所示。
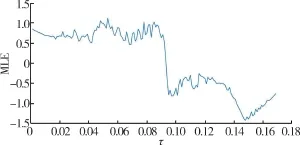
图2 最大李亚普诺夫指数计算结果
在接下来的数值模拟中,取τ≤0.092 0,此时MLE 为正,以保证系统处于混沌状态。 首先利用四阶Runge-Kutta 方法计算式(4),并生成2.1×105个数据点作为数据集U(t)。 然后,取出U(t)中前2 600个点作为训练集U1(t),剩余的数据作为加密集U2(t)。为了对RC 参数进行优化设置,先是研究了泄漏率α和储备池节点数N对预测效果的影响,结果如图3 所示。 从图3 中可以看出,当α∈[0.2,0.3]时,储备池计算可实现准确的预测,而N对预测结果影响不大。基于计算量和精确度的考虑,在数值研究中,取α=0.2,N=50,λ=1×10-8。 在训练阶段,需要舍弃前100个储备池初始状态值,并将剩下的2 500 个状态值和真实值U1代入式(3),计算得到Wout。
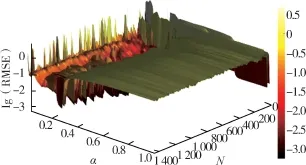
图3 泄露率α 和神经元数N 对预测准确率的影响
接下来,以图像作为传输内容对该保密通信机制进行验证。 图4(a)所示的图像“Lena”为待发送消息。 首先对该图像进行预处理,将其转化为一维向量h(t)。 通信过程中h(t) 将被U2加密,加密方式如下

图4 基于图像传输的保密通信验证
其中,λ1,λ2,K1,K2为密钥参数。 为提高安全性,K1和K2应设置为远远大于λ1和λ2,这里取λ1=0.15,λ2=0.1,K1=200,K2=150。S(t)为加密后的图像序列,将该序列转化为图片,可得到加密后图像,如图4(b)所示。
现在利用训练后的RC 来预测加密集U2(t),如果RC 的输出与U2同步,则表示可以进行解密。 计算结果如图5 所示。 如图5(a)所示,以x维度分量为例,RC 的输出仅可以和U2中对应维度实现短时间的同步。 为解决该问题,需要将TDL 系统中U2(t)的y分量U2y(t)反馈到预处理模块中,替换V′(t)中的V′y(t)变量,作为储备池计算的校准。
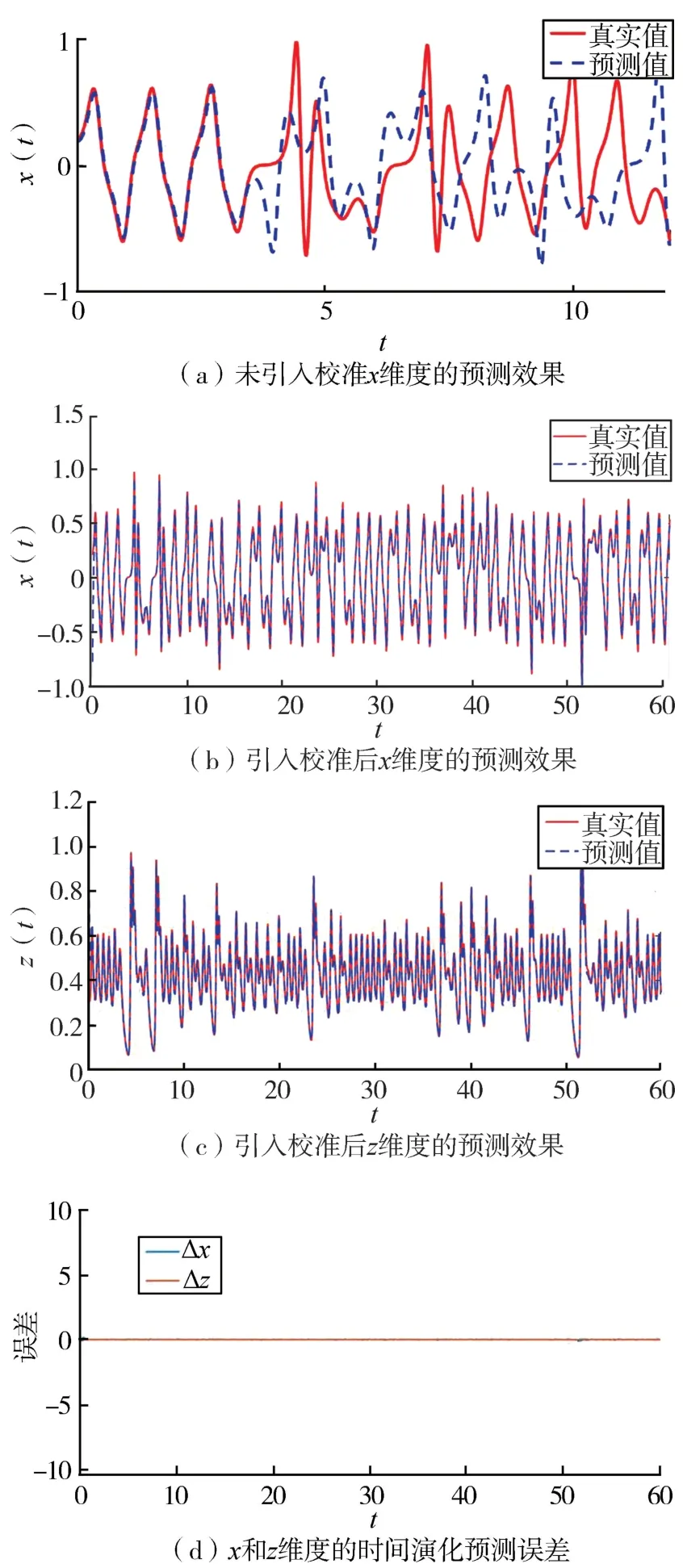
图5 针对TDL 混沌加密系统的预测
最终仿真结果如图5(b)和5(c)所示。 结果表明,RC 输出信号V(t)中的Vx(t)和Vz(t)分量可以快速地与用于加密的混沌信号U2x(t)和U2z(t)实现完全同步。 图5(d)为预测误差演化图,其也可以证明完全同步的实现效果。
基于RC 与加密信号的同步结果,可以对接收到的加密信息进行解密,解密操作如下
基于式(6),可以将加密后的信号h(t) 还原为三原色图片数据,如图5(c)所示。 经上述研究,可以证明该机制能够成功用于图像混沌保密通信。
2.2 MG 模型加密
为进一步证明本文提出的通信方案具有可行性与一般性,这里采用一维MG 模型作为另一类加密系统,该模型[15]的动力学方程为
其中,当τ=17 时,该系统处于混沌状态。 首先同样地采用步长为Δt=0.1 的四阶Runge-Kutta 方法,预先得到长度为6×105的数据集。 将前5 000 个点作为训练集,记作U1(t),用来训练接收端中的RC。 在训练过程中,α=0.3,储备池中神经元数量N=600。 利用式(3)同样可以计算得出有效输出权重矩阵Wout。
由于混沌的初值敏感性,训练后的储备池实际预测长度再次受到限制。 为解决该问题,针对该一维加密系统提出一种同步校准方法,即RC 的输入值由原始系统生成的真实数据,在经过约5 到6 个李雅普诺夫时间[29]后进行替代。 为验证该校准方法的有效性,对是否采用校准方法的结果进行了比较,如图6 所示。 可以看出,图6(b)中预测的长度相较于图6(a)更长更稳定。 图6(c)为同步误差图,可以用于进一步证明实现了混沌完全同步。
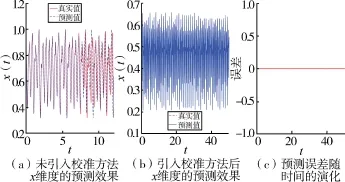
图6 针对MG 加密系统的预测结果
基于上述同步研究,接下来进行语音保密通信验证。 语音数据来源于清华大学开放的汉语语音数据库THCHS-30。 首先截取其中一段5 s 的语音信号,并通过采样得到信号h(t),如图7(a)所示。 采用公式S(t)={K1h(t)+K2U2(t)/(K1+K2)} 对语音进行加密,得到S(t)(见图7(b))。 最后,使用储备池计算机预测的V(t),对加密后信号进行解密,即:h(t)={(K1+K2)S(t)-K2U2(t)}/K1,得到的语音信号如图7(c)所示。 经过该研究,可以看出该机制可成功用于语音保密通信。
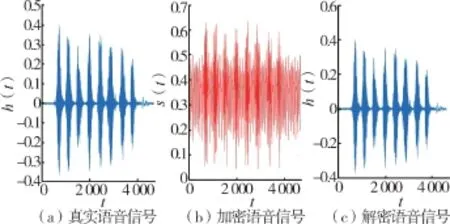
图7 基于语音信号传输的保密通信验证
2.3 实验设计与实现
为验证所提出通信机制的实用价值,基于FPGA 对该机制进行了硬件设计与实现,并通过真实视频加密传输进行实验验证。 该保密通信机制FPGA 设计框架如图8 所示。
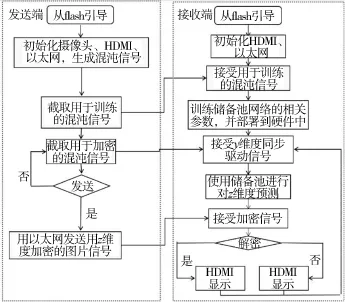
图8 基于TDL 加密系统的保密通信硬件设计框架
该机制的图像采集模块由PS 和PL 通过AXI4总线连接协同完成。 以TDL 系统作为加密系统为例,发送端的图像采集部分由ZYNQ 的PS 端对OV5640 图像传感器模块的寄存器组发送不同的寄存器值,完成摄像头的初始化采集工作。 再由PL 端自定义完成数据采集并进行以太网的初始化,混沌加密信号采用TDL 模型,基于该模型预先生成数据集。截取一部分作为训练集暂时保存后,发送给接收端。剩下的部分作为验证集,且用于信息加密,具体使用其z维度方向的数据对视频图像进行加密,并将x维度发送给接收端的解密模块,以进行z维度的同步解密。 视频的缓存使用VDMA IP 核,可以实现3 帧画面的缓存,从而避免画面的闪烁以及卡帧现象,ZYNQ的PL 端输出IP,将视频信号用HDMI 接口进行时序的呈现。 加密端封装电路IP 如图9 所示。
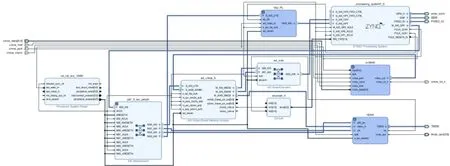
图9 发送端Block Design 综合图
图9 是基于Vivado 设计工具的RTL 代码设计后的综合结果,其含有一个复位系统,并使用同步时钟作为驱动信号,总线之间选择AXI Interconnect IP核实现所需功能。 OV5640 摄像模块中得到的图片数据需发送给AXI VDMA 的S_AXIS_S2MM 端口,每一帧的缓存给HDMI 进行图片的原始展示,最后通过TMDS 端发送给显示器。
接收端同样需要初始化HDMI 和以太网,并接受用于训练的混沌信号,使用软件的方式对混沌信号进行训练后得到关键参数,包括Wout、泄露率α和储备池大小N,并将这些参数部署到基于FPGA 实现的储备池计算模块中。 接收端封装IP 电路如图10 所示。
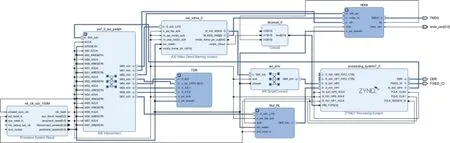
图10 接收端Block Design 综合图
图10 同样是通过RTL 代码实现并综合的结果,其复位系统和总线选择与加密端一致。 训练后的权重矩阵信息可以传输给TDR,从而得到储备池的状态信息X和输入权重Win矩阵。 基于Wout值,进行Mul_PL 乘法加速模块,可以计算出储备池的输出。 最后通过ZYNQ 7000 对数据进行解密,并保存发送给HMDI 模组显示结果。
RC 作为该机制的核心模块,其算法可以通过C++语言进行描述,并通过Vivado HLS 对其进行IP的封装,如图11 所示。 RC 模块主要是由1 个TDR的小IP 和3 个DDR3 外部储存构成,其主要算法过程由TDR 实现,并通过设置3 个输出端口保存输入矩阵Win、输出矩阵Wout以及储备池状态X。 接下来,可以使用TDL 对IP 的同步情况进行验证(y作为驱动信号),其结果如图12 所示。 从图12 可以看出,硬件实现的储备池计算在预测x和z维度均可实现较好的同步效果,也为下一步总体设计提供了RC 模块测试验证。

图11 RC 封装IP 图
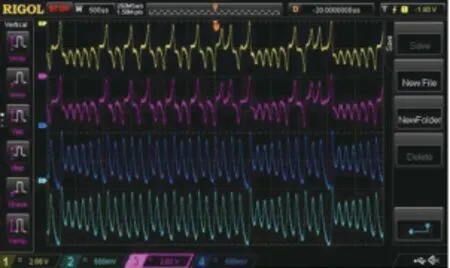
图12 对TDL 加密系统的长时间同步(示波器显示)
下面利用摄像头采集真实视频(水杯移动场景),基于上述硬件实现对该通信机制实验验证,并通过HDMI 接口演示,实验结果如图13 所示。 图13 中给出了原视频图像和加密后的图像,以及原图像和解密后的视频图像对比。 实验结果证明本机制可以进行真实视频加密通信。
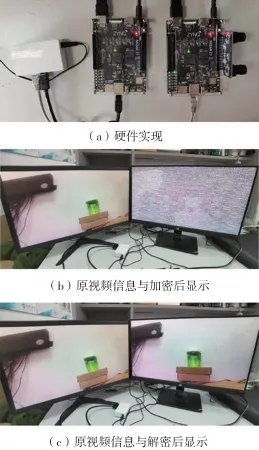
图13 利用提出的保密通信机制进行真实视频实时加密通信实验验证
上述实验中,视频图像的分辨率通常约为640×480,即一帧的大小为921 600 字节。 假设每秒要传输30 帧,那么至少需要一个长度为27 648 000/s 的加密数据序列。 因此,不经处理就传输未压缩的视频是不现实的。 解决这个问题的一个方法是采用重用加密数据。 利用该方法,基于所提出机制的通信速率可达到13.9 Mb/s。
2.4 噪声影响
本节讨论噪声对所提出保密通信机制的影响。基于白噪声模型,分别利用TDL 模型和MG 模型作为加密系统,研究了训练后的RC 在不同信噪比(Signal-Noise Ratios,SNR)下的预测性能。 信噪比定义为
其中,Ps为有用的信号功率,Pn为噪声功率。 预测效果采用均方根误差(RMSE)进行刻画
其中,V为预测信号,U2为不加噪声的原始信号。 计算结果如图14 所示。 对于TDL 加密系统,在SNR>45 dB 左右时,RMSE 可以保持在较低水平。 而当SNR 进一步降低时,RMSE 呈现出阶跃变化。 对于MG 加密系统,不同SNR 的RMSE 总体趋势表现为下降且波动。 因此,所提出的混沌保密通信机制采用三维加密系统比一维系统对噪声的鲁棒性更强。

图14 噪声对预测结果的影响
3 结束语
本文提出了一种基于机器学习——储备池计算混沌保密通信机制。 该机制的创新性在于其接收端可以与任意类型动力学系统产生的混沌加密信号实现混沌同步,解决了传统混沌保密通信无法自适应同步、耦合机制复杂等问题。 基于数值研究,以图像和语音为通信内容,分别采用三维TDL 模型和一维MG 模型作为混沌加密系统,验证了该机制的可行性。 同时,引入了分别针对三维和一维加密系统的校准方法,以实现混沌保密通信的长期稳定性。 基于FPGA 对所提出保密通信机制进行了硬件设计与实现,并基于真实视频实时加密通信,验证了该机制较强的实用价值。 此外,还考虑了噪声影响,证明了机制的噪声鲁棒性。 本文对新型混沌保密通信与机器学习交叉领域的研究具有一定的参考价值。

