认知星-地融合无线网络中的波束形成算法研究

鲁伟鑫，李佳保，安 康，沈文科，王三喜

(1.陆军指挥学院，江苏 南京 210000 2.国防科技大学 第六十三研究所，江苏 南京 210007)

卫星通信系统以其通信距离远、覆盖范围广、组网灵活和不易受自然灾害影响的独特优势，在军事和民用领域应用广泛，并且拥有广阔的发展前景。卫星通信不仅是军事通信中的重要手段，在许多民用领域，如广播、导航、救援和应急通信等领域也是广泛应用，是多个国家重点关注的重要技术［1］。 虽然卫星通信有着得天独厚的优势，但也不可避免地存在一定的弊端，首要的一个问题就是由于卫星信号的广播特性，卫星通信的安全问题需要重点考虑，随着卫星频谱资源的日益紧缺，同时地面通信频谱资源存在未被充分利用的情况，认知星-地融合网络中的物理层安全问题变得火热起来，在这一领域拥有巨大的研究潜力［2－3］。

近年来，关于卫星通信系统研究的成果较多，文献［4］针对卫星通信系统中的功率控制方案，研究了系统中的发射功率最小化问题，约束条件为每个用户的安全速率满足要求，提出对应的波束形成方案对优化问题进行求解。 文献［5］在假设窃听用户的信道信息完全已知和部分已知的情况下，以卫星系统发射功率最小化为目标函数，提出4 种波束形成方案来研究卫星通信系统下行链路安全问题。 文献［6］研究了基于网络编码的卫星通信系统安全问题，优化问题的目标函数为安全速率最大化，最优波束形成权矢量通过半正定规划方法求得。 文献［7］研究了多波束卫星下行网络的安全传输问题，目的是在满足卫星总发射功率约束的前提下，使得系统所有合法用户的可达安全速率之和最大化，提出了一种鲁棒波束形成（BF）方案，使原始非凸的优化问题转化为满足凸形式的优化问题。 文献［8］重点研究了多波束卫星通信系统中基于非正交多址（NOMA）的鲁棒波束形成优化问题，每个用户的服务质量满足标准的同时，在信道状态信息（CSI）已知和不完全已知的情况下，优化卫星总发射功率。

随着卫星通信网络的不断发展，关于认知星-地融合网络的研究也不断深入。 在认知星-地融合网络中，运用认知无线电（Cognitive Radio，CR）技术可以提高频谱资源的利用率，实现卫星网络与地面网络共享频谱资源。 文献［9］建立了认知星-地融合场景，介绍了相应的认知技术以及认知星-地融合网络的波束形成技术。 文献［10］研究了共享频谱的卫星通信网与地面蜂窝网中的物理层安全问题，地面基站作为一个绿色的干扰源来提升卫星通信系统的安全性能。 文献［11］总结了星-地融合认知网络中的常用算法，并分析了频谱感知算法的重要性和优缺点。 文献［12］在卫星主用户干扰门限受约束情况下，研究了地面次级网络传输速率最大化时的功率分配方案。 文献［13］介绍了低轨卫星在卫星通信中的重要作用以及认知无线电技术在低轨卫星通信系统中的应用和发展。 文献［14］研究了混合卫星-地面无线网络中的传输功率最小化问题，约束条件为卫星和地面次级用户满足中断概率的限制。文献［15］通过优化时间分割因素的最佳合作传输方案，使得认知星-地网络的频谱效率最大化，在叠加式认知卫星地面网络中，二级地面网络以时间分割的方式与一级卫星网络合作进行频谱接入。 文献［16］研究了混合卫星地面中继网络（HSTRN）中的安全传输问题，其中窃听者可以窃听来自卫星和中继的传输信息，为了有效地保护信息在这两个阶段不被窃听，考虑了中继的合作干扰，在中继的总功率约束下，干扰信号被优化为最大保密速率。 目前，基于波束形成算法对认知星-地融合网络中的物理层安全问题研究相对较少，本文研究内容弥补了这一不足，认知星-地融合无线网络结合了卫星网络和地面蜂窝网络的优势，也弥补了各自的不足，未来认知星-地融合无线网络中的物理层安全问题研究势必会成为新的研究热点。

本文研究了认知星-地融合无线网络中的波束形成算法，认知星-地融合无线网络包含两个子网络：卫星通信网络和地面蜂窝网络，卫星通信网络为主网络，地面蜂窝网络为次级网络。 首先，以系统总发射功率最小化为目标函数，卫星主用户的可达安全速率和次级用户的通信速率满足需求为约束条件建立优化问题。 然后，提出迫零波束形成算法、门限值替代算法和黄金分割算法对优化问题进行求解，并比较3 种算法在求解优化问题时的性能优劣。 最后仿真结果表明，在其他限制条件相同时，黄金分割算法在求解优化问题的最优解时更加高效，同时可以节省更多的功率。

1 系统模型

如图1 所示，本文研究了认知星-地融合无线网络中的波束形成算法，该无线融合网络包含主网络和地面次级网络两个子网络，其中，主网络为卫星通信网络，地面次级网络为地面蜂窝网络。 卫星通信主网络包含一个卫星主用户（Primary User，PU）和一个地面窃听用户（Eavesdropper，Eve），地面次级网络包含一个地面基站（Base Station，BS）和一个地面次级用户（Secondary User，SU）。 为了提高频谱利用率，卫星通信主网络和地面次级网络频谱共享，因此网络间会存在干扰现象。 卫星通信主网络在进行通信时，卫星所发射的信号会干扰次级用户，地面基站所发送的信号也会对卫星主用户进行干扰，窃听用户能够同时接收到卫星和地面基站信号。 本文所研究的认知星-地融合无线网络中，假设卫星和地面基站分别装备有N1和N2根天线，卫星主用户、地面窃听用户和地面次级用户分别安装单根天线。

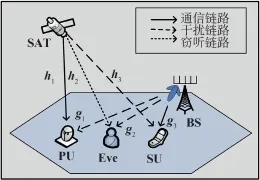
图1 认知星-地融合无线网络系统

2 信道建模

2．1 卫星通信网络下行链路信道建模

由于卫星通信网络与地面蜂窝网络通信信道的不同特性，在进行信道建模时需考虑二者独特特性所造成的影响。 首先，进行卫星通信网络信道建模，本文所研究的内容主要考虑雨衰和波束增益的影响。

第一部分是大气层中雨衰造成的影响。 当信号频率在10 GHz 以上时，在传输过程中会受到包括大气、环境、衍射、电离层等影响，可以把这些影响总结为雨衰造成的影响。 本文应用ITU-R P.618-10 中的内容，将雨衰造成的影响准确地进行信道建模［17］，用log 函数和指数函数对信道衰减函数部分进行数学估计。 综合上述条件和参考文献的内容，可以通过数学建模方法估计出雨衰系数的数学估计表达式为

其中，ϕ为［0，2π） 区间中均匀分布的N0×1 相位矢量。 功率增益β的单位用dB 表示，可以写成βdB＝20 log10β，βdB为服从对数随机正态分布变量ln（βdB）～ N（μ，δ），μ和δ取决于信号接收者的位置、工作频率、极化方式和高度角。

第二部分为波束增益。 波束增益取决于信号接收端的位置角和卫星天线工作模式，参考文献［18］，可以估计出第m个信号接收端的波束增益表达式为

同时，um可以表示为

其中，Jν为第v阶的贝塞尔函数，θm为第m个接收用户与卫星波束中心相对卫星的角度， （θ3dB）m为其对应的3-dB 角。

定义N1×1 的波束增益矢量b为第m个接收用户的波束增益矢量，根据式（2）和式（3），相对应的接收用户的卫星信道可以表示为

其中，b为波束增益矢量，为雨衰矢量。

2．2 地面蜂窝网络无线信道建模

本文假设地面无线衰落信道服从相关瑞利衰落分布，则第m个接收用户与地面基站间的信道矢量为

其中，Lm为多径的数目，ρm，l为信道衰落系数，αl∈为第l条路径的到达角，为平均簇到达角，Δα为散射角度。 根据地面基站所采用的均匀线阵天线结构，阵元导引矢量am（αl） 可表示为

2．3 信号模型建立

前面内容对系统模型和信道模型进行了介绍，接下来根据前面介绍的内容建立地面各个接收用户处所接收到的信号模型。 在本文所研究的星-地融合无线网络中，假设卫星发送信号为s1， 在发送前经过波束形成权矢量进行加权处理，卫星发送信号s1满足E［｜s1｜2］＝1。 假设地面无线网络中基站发送给地面次级用户的信号为s2，信号在发送前地面基站通过波束形成权矢量进行加权处理，地面基站发送信号满足E［｜s2｜2］＝1。 卫星发送端和地面基站发送端的发送信号x1和x2可以分别表示为

已知发送端的发送信号，则可将地面卫星主用户、窃听用户和地面次级用户接收到的信号分别表示为

根据式（12）至式（14）［19］，可以计算出卫星主用户的可达安全速率为

其中，中括号中内容代表［x］＋＝max（x，0）。

3 算法方案设计

本节首先根据认知星-地融合无线网络中的波束形成算法建立优化问题，假设各个节点信道状态信息完全已知，以卫星和地面基站的发射功率最小化为目标函数建立优化问题，约束条件为卫星主用户的可达安全速率和地面次级用户的通信速率满足要求。 迫零波束形成算法、门限值替代算法和黄金分割算法将原始优化问题转化为标准的半正定规划问题，进而求解得出最优波束形成权向量，最后对比分析3 种算法的性能优劣。

3．1 优化问题的建立

本节所研究的优化问题的目标函数为卫星和地面基站的发射功率最小化，约束条件分别为卫星主用户的可达安全速率和地面次级用户的通信速率满足要求，通过求解出最优波束形成权矢量来达到这一目的，优化问题的数学表达式如下

在本节的研究中，联合优化设计方案的灵活性可以实现卫星和地面基站的功率协同，节省一部分性能，同时，地面基站可以显著简化机载信号的处理负担，减少相关实施成本。 接下来，针对不同的波束形成设计方案，讨论具体的求解办法。

3．2 迫零波束形成算法

本节采用的是卫星信号对地面窃听用户迫零的波束形成方案，也就是窃听用户在接收端接收到的卫星有用信号功率趋近于零，这样可以近似看做卫星信号没有发生泄漏，同时提升卫星主用户的通信速率。 因此，迫零波束形成方案需要满足如下限制

应用迫零波束形成方案时，要求卫星天线的空间自由度最少为1＋K，需要N1＞（1＋K） 根足够的天线满足这一限制。 应用迫零波束形成方案后，针对优化问题式（16）的第一个约束条件，卫星主用户的可达安全速率可以表示为

接下来，优化问题式（16）可以表示为

为了求解上述优化问题式（19），通过引入新的矩阵变量和矩阵的迹，将优化问题式（19）转化为标准的半正定规划问题。 引入的新矩阵变量为W1＝，它们是共轭对称的Hermitian矩阵。 通过引入矩阵变量和矩阵的迹，可以将优化问题式（19）转化为如下的半正定规划形式

其中，Tr（W） 为矩阵W的迹， rank（W） 为矩阵W的秩，H1为卫星与卫星主用户之间信道矢量的自相关矩阵，H2为卫星与地面窃听用户之间信道矢量的自相关矩阵，H3为卫星与地面次级用户之间信道矢量的自相关矩阵。 同时，G3为基站与地面次级用户之间信道矢量的自相关矩阵，G2为基站与窃听用户之间信道矢量的自相关矩阵，G1为基站与卫星主用户之间信道矢量的自相关矩阵。 为了更便捷地求解优化问题式（20），应用半正定松弛的方法松弛rank（W1）＝1 和rank（W2）＝1 的约束条件［20－21］。因此，优化问题式（20）可以进一步表示为

优化问题式（21）被转化为标准的SDP 问题，可以采用标准的数学工具包对优化问题式（21）求解，本文中采用的数学工具包为凸优化包［22］。 另一方面，迫零波束形成算法可以降低优化问题式（21）的求解难度。

3．3 门限值替代算法

通过观察可以发现，迫零波束形成算法的优化过程可以使优化问题的求解更加容易，但需要额外增加较为严苛的约束条件，同时会造成一定的资源消耗。 本节通过对优化问题的化简，发现增加两个门限值也可以对优化问题进行求解，化简后的优化问题如下

针对优化问题式（23），与迫零波束形成方案类似，引入新的矩阵变量和矩阵的迹，经过数学转换可将优化问题式（23）重新表示为

通过半正定松弛的方法， 移除非凸的rank（W）＝1 的约束条件，则满足凸形式的优化问题式（24）可以重新表示为

由于引入的两个已知门限值ε1和ε2是固定值，不难发现优化问题式（25）是满足凸形式的，是一个标准的SDP 问题，可以使用标准的凸优化包进行求解。

3．4 黄金分割算法

本节通过引入新变量的方式直接对优化问题式（16）进行求解。 将相对应的变量代入优化问题式（16），则对应的优化问题可以表示为

通过观察优化问题式（26），发现其不是一个二次约束二次规划问题，不能直接用标准凸优化包进行求解。 为了求解优化问题式（26），引入新的辅助变量t，其物理意义为窃听用户接收到信号的信干噪比小于一定的值，引入新的辅助变量t后，可以将优化问题重新表示为

通过观察优化问题式（27）可以发现，t作为中间的辅助变量增加了一个约束条件，经过数学变换后，优化问题可以重新表示为

如果辅助变量t不确定会导致优化问题式（28）是非凸的，因此首先赋予辅助变量t一个初值，然后再通过黄金分割算法搜索出t的最优值，此时联合优化问题的目标函数值也满足要求。

接下来引入新的矩阵变量和矩阵的迹，通过半正定松弛的方法移除非凸的rank（W）＝1 的约束条件，优化问题式（28）可以重新表示为

当辅助变量t为确定值时，可以发现优化问题式（29）是满足凸形式的，是一个标准的SDP问题，接下来使用标准的凸优化工具包对其进行求解。

将优化问题式（29）的目标函数当做辅助变量t的函数，记为P（t）。 当t固定时，优化｛W1，W2｝ 的值求解优化问题式（29）的目标函数的最小值，也就是最小化P（t） 的值。 对于单峰极小值优化问题，黄金分割搜索法的效率是非常高的，对于本节内容采用黄金分割搜索法主要的优化过程可以总结如下：每次迭代过程中，最优t值所处的区间逐渐缩小，当搜索区间的长度小于搜索容限tol时，优化过程停止，此时的t值即为使目标函数达到最优值的t值。 初始的搜索区间为［a，b］， 给定不同的初值t1和t2， 分别求解优化问题式（29）来求解对应的P（t） 值。 将P（t） 值相对较小的t值保存，通过不断更新搜索区间和对应的t值，最终通过优化得到最优的P（t） 值，算法具体过程如算法1 所示。 随着搜索区间的不断缩小，P（t） 的取值也越来越小，当搜索区间的长度小于规定的搜索容限时，算法停止，此时的P（t） 值即为最优值。

算法1黄金分割算法

接下来对W采用特征值分解的方法来得到最优权向量w［23］。 在分解过程中，W可以被分解为一系列秩为1 的矩阵

其中，λn表示W的第n个特征值，en表示第n个特征值对应的特征向量。 因此，式（30）可以表示为

4 仿真结果与分析

本节通过计算机仿真对迫零波束形成、门限值替代和黄金分割3 种算法结果进行评估验证。 假设卫星天线数目N1＝4，地面蜂窝网络中地面基站天线数目N2＝8。 假设卫星主用户坐落在卫星波束中心，卫星主用户、地面窃听用户和次级用户分布在同一个卫星波束中。 地面蜂窝网络中的基站装备均匀线性阵列天线，卫星主用户、地面窃听用户和地面次级用户在地面蜂窝网中的相对位置角分别为α1＝40°，α2＝20°和α3＝0°。 卫星信道衰减函数部分用log 函数进行数学估计，参数设置如表1 所示［24］。另外，代表卫星主用户、窃听用户和次级用户产生的均值为0 的加性高斯白噪声，仿真过程中假设。

表1 认知星-地融合无线网络中的系统参数

图2 仿真了应用黄金分割算法求解优化问题时，系统总发射功率随迭代次数增加的变化情况。其他仿真参数分别为：主用户安全速率门限值R1＝8 bit／s／Hz， 次 级 用 户 通 信 速 率 门 限 值R2＝2 bit／s／Hz。 可以发现，随着仿真不断进行，迭代次数逐渐增加，应用黄金分割算法求解优化问题时，系统总发射功率先逐渐减小，最后趋于稳定。 仿真结果表明，黄金分割算法求解优化问题是有效的，可以求解得到该优化问题目标函数，也就是系统总发射功率的最小值。

图2 系统发射总功率随迭代次数变化情况

图3 描绘了地面基站发射功率波束形成权矢量归一化的信号方向图。 图3 标出了卫星主用户、窃听用户和地面次级用户的位置角度信息，对应的角度与仿真设置的参数相同，可以发现波束主瓣对准地面次级用户，旁瓣对准窃听用户，零点对准卫星主用户，物理意义上可以解释为，在保证地面次级用户通信质量的同时，地面基站通过对窃听用户产生较大的干扰，对卫星主用户产生较小的干扰，提升卫星通信系统的安全性能。

图3 归一化的信号方向图

图4 描绘了系统总发射功率随主用户可达安全速率需求的变化情况。 其他仿真参数分别为：地面次级用户通信速率门限值R2＝2 bit／s／Hz， 门限值替代算法中ε1＝－3 dB，ε2＝10 dB。 可以看到对3种算法，系统总发射功率都随着卫星主用户可达安全速率需求的增加而增加，迫零波束形成算法和门限值替代算法的总发射功率始终高于黄金分割算法，可见黄金分割算法可以为系统节省更多的能量。当卫星主用户可达安全速率需求较小时，迫零波束形成算法所需要的系统总发射功率明显高于门限值替代算法。 随着卫星主用户可达安全速率增加，当卫星主用户安全速率门限值大于2 bit／s／Hz 时，门限值替代算法的系统总发射功率高于迫零波束形成算法；随着卫星主用户可达安全速率需求持续增加，二者差距逐渐稳定。 当卫星主用户可达安全速率需求较低时，迫零波束形成算法中迫零约束条件增加的功率较大，因此系统总发射功率较高。 随着卫星主用户可达安全速率需求的增加，门限值替代算法中地面基站的信号干扰造成了更大的影响，使门限值替代算法中系统总发射功率略高于迫零波束形成算法。 通过观察可以发现，相较于其他两种算法，黄金分割算法能够节省更多的功率，由此可见黄金分割算法在解决该优化问题时具有一定的高效性。

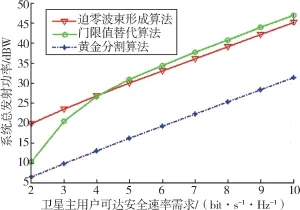
图4 系统发射总功率随主用户可达安全速率需求变化情况

图5 展示了系统总发射功率随次级用户通信速率门限的变化情况。 其他仿真参数分别为：卫星主用户可达安全速率门限值R1＝1 bit／s／Hz， 门限值替代算法中ε1＝－3 dB，ε2＝10 dB。 3 种算法下，系统总发射功率都随着次级用户通信速率门限增加而增加，当次级用户通信速率门限较小时，迫零波束形成算法所需的系统总发射功率最大，门限值替代算法次之，黄金分割算法最小。 随着次级用户通信速率门限逐渐增加，3 条曲线的差距逐渐减小，最后混合为一条曲线。 当次级用户通信速率门限较低时，迫零波束形成算法由于需要额外的功率满足迫零条件，所以发射功率较高。 门限值替代算法相较于黄金分割算法误差较大，所需要的发射功率较高。 随着次级用户通信速率门限值增大到一定程度时，系统发射功率足以弥补迫零条件和算法带来的误差，所以三条曲线重合。

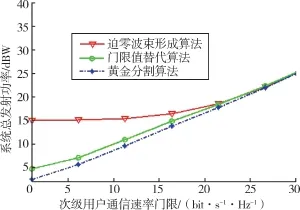
图5 系统发射总功率随次级用户通信速率门限变化情况

5 结束语

本文重点研究了认知星-地融合无线网络中的波束形成算法，存在地面窃听用户的卫星网络作为主网络与地面次级网络共享频谱资源，卫星主网络与地面次级网络共同构成认知星-地融合无线网络。优化问题的目标函数是系统总发射功率最小化，约束条件为卫星主用户的可达安全速率受限以及地面次级用户的通信速率满足要求。 认知星-地融合无线网络中各节点的信道状态信息完全已知，通过迫零波束形成算法、门限值替代算法和黄金分割算法对优化问题进行求解，并对3 种算法的具体求解过程进行分析推导。 最后，通过计算机仿真对3 种算法的性能进行评估验证，由仿真结果可知，在其他参数相同时，黄金分割算法在求解优化问题时具有一定的高效性和优越性。