智能超表面辅助双小区NOMA系统下行低功耗传输方案研究

过仕安，王 鸿

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

第五代移动通信系统（5G）已在全球范围内部署，按照“十年一代”的发展规律，对第六代移动通信系统（6G）的研究已经得到了学术界与工业界的广泛关注。 智能超表面（Intelligent Reflecting Surface， IRS）因其在频谱效率与功率效率等方面的优势，被认为是下一代移动通信系统的关键性技术之一［1－2］。 IRS 是由大量无源反射器件构成的平面阵列，每个反射单元都具备独立且实时操控传输信号相移与幅度的能力，从而可根据实际需要重新配置无线传播环境， 为6G 带来一种全新的通信范式［3－4］。

此外，非正交多址接入（Non-Orthogonal Multiple Access， NOMA）在频谱效率和多址接入方面具备极大的潜力，是未来无线通信网络中有应用前景的多址接入技术。 NOMA 的显著特点是利用叠加编码方案，允许多个用户占用相同的时频资源进行并发传输［5－6］。 文献［7］研究了多输入多输出（Multiple-Input-Multiple-Output， MIMO）NOMA 网络中功率分配与用户配对问题，仿真结果表明，提出的NOMA传输方案的性能明显优于其他基准方案。 并且已有研究证明，与传统的正交多址接入（Orthogonal Multiple Access， OMA ）相比，NOMA 在性能方面可获得更低的中断概率和更高的遍历容量［8－9］。

鉴于IRS 与NOMA 各自的技术特点，IRS 和NOMA 的融合可充分发挥IRS 在信道配置方面的作用，进一步释放NOMA 利用信道差异化的潜能，因而IRS 和NOMA 融合研究已经吸引了学者们的关注。 文献［10］从传输功耗的角度研究了IRS 在NOMA 系统功率效率方面的有效性，并提出了最小化系统传输功率算法。 文献［11］研究了具有离散相移的IRS 辅助NOMA 系统，根据基站与用户之间是否存在直连通道推导了系统的中断性能。 文献［12］研究了在NOMA 系统中部署IRS 提高小区边缘用户的数据传输速率，从而提升蜂窝小区的无线网络覆盖质量。 文献［13］通过设计IRS 无源波束成形矩阵，研究了IRS 辅助NOMA 系统的中断概率以及遍历容量。 上述关于IRS 辅助NOMA 系统研究成果［10－13］已经很好地验证了IRS 与NOMA 融合系统可获得的性能增益，但是考虑的系统模型都局限于单小区场景。

在IRS 辅助的多小区蜂窝系统中，存在更为复杂的信号传输以及小区间干扰等问题，系统参数优化设计的难度也将变得更大。 针对IRS 辅助的两小区无线网络，文献［14］考虑了小区边缘用户的公平性，通过联合优化基站的发射波束成形和IRS 的相移系数来最大化小区边缘用户的最低可达速率，然而，文献［14］并未考虑采用NOMA 技术。 为了解决这一不足，文献［15］将IRS 集成到两小区NOMA 网络中，将IRS 部署在小区边缘以提高边缘用户的传输速率，并进一步设计了有效的优化算法，以最小化IRS 辅助多小区NOMA 上行系统的传输功耗。

目前，对于IRS 辅助的多小区NOMA 系统的研究还处于起步阶段，尤其关于两小区协作多点（Coordinated Multi-Point， CoMP）传输场景的研究更少。 因此，本文研究了基于CoMP 传输的IRS 辅助双小区NOMA 下行系统发射功耗最小化问题。 本文的创新工作总结如下：（1） 建立了IRS 辅助双小区NOMA 系统下行优化设计架构，同时考虑了采用CoMP 传输技术提升小区边缘用户的传输质量。 在满足用户的服务质量（Quality of Service， QoS）和相移向量元素单位模的双重约束下，本文通过联合优化用户的功率分配和IRS 反射单元的相移，实现IRS 辅助双小区NOMA 系统传输功耗的最小化。（2） 由于构建的下行系统功率最小化问题是非凸的，且各优化变量之间是高度耦合的，很难直接求解，本文利用功率分配系数与相移之间的关系，将原来的功率分配和相移联合优化问题转化为纯相移优化问题。 进一步地，本文提出了一种基于顺序相位旋转技术求解转化后的相移优化问题。 仿真结果表明，本文提出的优化算法在总发射功耗方面明显优于其他基准方案。

1 系统模型

本文考虑一个双小区IRS 辅助NOMA 下行传输系统，系统模型如图1 所示，其中，两个单天线基站服务两个单天线小区中心用户与一个单天线小区边缘用户，并且一个配备N个无源反射元件的IRS部署在小区边缘提升边缘用户的传输质量。 基站的覆盖半径定义为Rbase，小区中心用户随机分布在以基站为中心、以Rcenter为半径的圆形区域内。 IRS 的覆盖半径定义为Rs， IRS 被部署于两个基站的中间，小区边缘用户随机分布在以IRS 为中心、以Rs为半径的圆形区域内。 在考虑的系统中，小区中心用户由与其最近的基站服务，而小区边缘用户则由两个基站采用CoMP 技术同时服务。

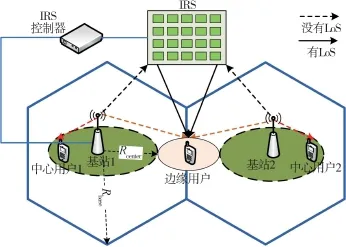
图1 系统模型

由于在实际的传输环境中，存在障碍物阻挡与严重的路径损耗，被IRS 反射两次及以上的信号可以忽略不计［14］。 并且，由于发射级联信道的双路径损耗和障碍物阻挡，对于小区中心用户来说，接收到的来自另一个小区的或被边缘IRS 反射的信号很微弱，也可忽略不计［14－15］。 那么，基站i（i∈｛1，2｝）服务的中心用户i的接收信号可以表示为

其中，hi，C表示基站i与其服务的小区中心用户之间的信道系数；wi，C表示中心用户处的加性高斯白噪声，其服从均值为0、方差为的复高斯分布；yi表示基站发送的叠加信号，可进一步表示为

其中，yi，C和yi，E分别表示小区中心用户和边缘用户的发送信号；si，C和sE分别表示小区i发送给中心用户和边缘用户的归一化功率信号；αi，C和αE分别表示小区i分配中心用户和边缘用户的发射功率系数。

相应地，小区边缘用户接收来自两个基站的总信号可以表示为

其中，hi，E表示基站i与小区边缘用户之间直连的信道系数；hi，R表示基站i与IRS 之间的信道向量；hR，E表示IRS 与小区边缘用户之间的信道向量；wE表示边缘用户处的加性高斯白噪声，其服从均值为0、方差为的复高斯分布；Θ表示IRS 相移矩阵，本文的Θ被定义为

其中，｛κn ＝ejθn，1 ≤n≤N｝。 考虑实际系统的可实现性，本文考虑离散的相移模型。 具有D个量化比特且均匀量化的离散相移集合可以表示为

相应地，每个离散相移需满足：θn∈D，1 ≤n≤N。

在本文考虑的系统模型中，由于基站和用户之间的直连信道传播距离长、散射范围大、视距路径（LoS）易被阻塞，所以假设基站和用户之间直连信道的小尺度衰落均遵循瑞利衰落［16］。 那么，基站i与其小区中心用户之间的信道系数可以表示为

类似地，基站i与小区边缘用户之间的直连信道可以表示为

其中，di，C和di，E分别表示基站i与中心用户和边缘用户之间的传播距离；βB，C和βB，E分别表示基站i到中心用户和边缘用户直连信道的路径损耗指数；zi，C和zi，E表示小尺度衰落，其服从均值为0、方差为1 的复高斯分布。

基站i与IRS 之间的直连信道向量可以表示为

其中，di，R表示基站i与IRS 之间的传播距离；βi，R表示基站i与IRS 之间的路径损耗指数；小尺度衰落zi，R服从均值为0、方差为1 的复高斯分布；ΦT表示IRS 反射单元之间的接收相关矩阵。

由于IRS 可选址部署且IRS 与边缘用户之间的传播距离较短，二者之间存在视距（Line of Sight，LoS）传播路径，所以，相应的信道向量可以建模为莱斯衰落模型

其中，dR，E表示IRS 与小区边缘用户之间的传输距离；βR，E表示IRS 与小区边缘用户之间的路径损耗指数；K表示莱斯因子；z0表示LoS 信道的系数；小尺度衰落zR，E服从均值为0、方差为1 的复高斯分布；表示IRS 反射单元之间的发送相关矩阵。

由于小区中心用户的信道条件明显优于小区边缘用户，根据下行NOMA 系统解调原则，小区中心用户先解调小区边缘用户信号，并采用串行干扰删除（Suceessive Interference Cancellation， SIC）技术移除小区边缘用户信号，然后再解调小区中心用户自身的信号。 当边缘用户解调信号时，中心用户信号被视为干扰。 因此，中心用户解调边缘用户的信干噪比（Signal-to-Interference-Plus-Noise-Ratio， SINR）可表示为

在边缘用户信号解调完成后，中心用户从总接收信号中删除边缘用户信号，再解调自身信号的SINR 为

由于小区边缘用户的传输功耗高于小区中心用户，当小区边缘用户在解调自身信号时，中心用户的信号被视为干扰。 因此，小区边缘用户解调自身信号的SINR 可表示为

2 问题建模及转化

本文的目标是通过联合设计基站的功率分配系数和IRS 的无源波束成形矩阵来最小化系统的总发射功耗。 在保证每个用户最低SINR 阈值的约束下，以最小化系统总发射功率为优化目标函数，优化问题可表示为

其中，｛αC，i，i ＝1，2｝、αE、Θ为优化变量，和分别表示小区中心用户和边缘用户的SINR 阈值，P表示两个基站的总发射功率之和；约束条件C1，C2 和C3 是为了确保用户的QoS，约束条件C4表示每个相移系数的单位模约束。

由于在原始优化问题P0中，各优化变量之间是高度耦合的，很难直接求解，本文的求解思路是将原联合优化问题P0转换为纯相移优化问题。 利用矛盾论可以得到，当优化问题P0取得最优解时，约束条件C1 取等号。 因此，可以将基站i的小区中心用户所需的传输功率表示为

将式（14）和式（15）进行化简得到

为了简化上述表达式， 令相移向量v ＝， 级 联 信 道 向 量gi ＝可以进一步表示为

为了保证边缘用户信号同时在中心用户与边缘用户处能够成功解调，需在中取较大者作为边缘用户所需的传输功率此时，优化问题P0可以转化为问题P1

在优化问题P1中，优化变量已经由式（13）给出。 由式（18）可知，有关，由于已经确定，所以可通过v表示。 因此，实际上优化问题P1仅与IRS 相移偏移向量v有关。 至此，基站传输功率分配和IRS 离散相位偏移联合优化问题也就成功转化为单纯的相移优化问题。

可以明显地看出P2中的优化变量仅包含相移向量v，但是由于恒模约束条件的限制，优化问题P2仍是非凸的，其最优解通常不可直接求解，所以本文将提出一种基于顺序相位旋转算法获得相移优化方案。

3 相移优化设计方案

本节提出一种迭代法求解优化问题P2。 在每次迭代中，采用顺序相位旋转算法求得各个相位旋转量的最优解，并将第t－1 次迭代的解依次旋转N次就可得到第t次迭代的解，可以表示为

求得最优解v∗后，再利用模运算将v∗中的每个相移归一化到［0，2π） 区间。

其中

在优化问题P3中只有一个优化变量φn， 可以用一维搜索方法求得最优解，即

由于在实际系统中，IRS 相移可以通过PIN 二极管实现，相移集合空间D的量化比特数等于PIN二极管的数目［17］。 考虑到IRS 反射单元的尺寸，PIN 二极管的数目不可能很多，因此搜索的空间不会很大，提出算法不会带来较大的搜索复杂度。

4 仿真结果与分析

本节对提出的优化算法进行仿真分析，详细的仿真实验参数如表1 所示。 并与以下4 种基准方案进行了性能对比，分别为随机相移IRS 辅助NOMA系统、零相移IRS 辅助NOMA 系统、IRS 辅助OMA系统和无IRS 的NOMA 系统。

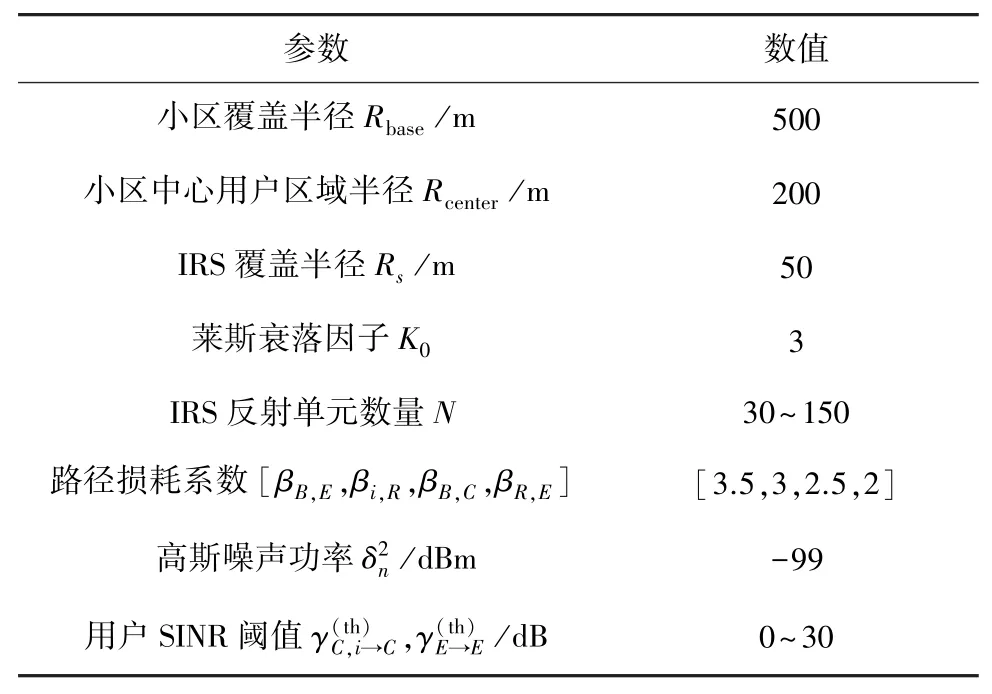
表1 仿真参数设置

图2 展示了系统发射总功率与IRS 数量之间的关系。 从图2 中曲线走势可以看出，系统总发射功率随着IRS 反射单元数量的增加而减小，这是因为IRS 数量的增加可以增强有用信号的功率，并抑制干扰的功率。 此外，可以发现本文提出的优化方案明显优于其他基准方案，其原因是本文对功率分配系数与IRS 相移矩阵进行了联合优化。 因此，可以得到IRS 能够有效降低多小区NOMA 系统的总发射功率，并且随着IRS 反射单元数量的增加，优势变得更加显著。

图2 系统发射功率和IRS 反射单元数量的关系

图3 展示了不同SINR 需求下，系统发射总功率与用户SINR 阈值之间的关系。 从图3 中曲线趋势可以看出，系统的总发射功率随着SINR 阈值单调增加，其原因是为了获得更高的QoS，需提高基站的发射功耗。 与随机相位和零相位的IRS 辅助系统相比，顺序相位旋转算法可以降低发射功率消耗大约10 dB，这是因为本文提出的优化方案以降低功耗为目标，对用户功率分配和IRS 相移进行联合优化。 IRS 辅助NOMA 下行系统的发射功率低于IRS辅助OMA 系统，原因在于NOMA 系统相较于OMA系统存在性能优势。 IRS 辅助NOMA 下行系统的发射功率低于无IRS 辅助的NOMA 系统，说明了IRS可以有效提高有用信号的传输性能。

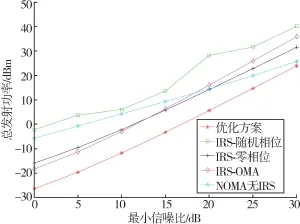
图3 系统发射功率和用户SINR 阈值的关系

5 结束语

本文通过联合优化基站处的功率分配系数以及IRS 处的相位偏移矩阵，研究了双小区IRS 辅助NOMA 下行系统传输功率最小化问题。 由于原始优化问题是非凸的，本文进一步将用户功率分配和IRS 相移的联合优化转化为纯相移优化问题，并提出了顺序相位旋转算法解决转化后的相移优化问题。 仿真结果表明，本文提出的优化方案在传输功率消耗方面优于其他基准方案。