左截断右删失数据下伽马分布的参数推断
周旭,田茂再,2
(1. 新疆财经大学 统计与数据科学学院,新疆 乌鲁木齐 830012;2. 中国人民大学 统计学院,北京100872)
在生存分析的实际研究中,数据常伴随截断和删失。数据的不完整给统计推断过程带来困难,若直接忽略截断和删失数据所包含的信息,往往会导致估计结果不尽人意。近几年对于截断和删失同时存在的数据类型进行寿命分布的参数推断变得越来越普遍,在截断和删失同时存在的数据中,参数估计使用MLE(极大似然估计)方法是很困难的,而且由于伽马函数的存在,对不完全伽马函数的对数求最大化并不简单,矩估计是一种数值方法,且矩估计量具有很好的一致性和渐近正态性,能够引入潜在数据对参数进行有效估计。伽马分布是统计学中一种应用较为广泛的连续型寿命分布,在概率论中与众多分布有着密切的联系。在此背景下,选择对左截断右删失数据下伽马分布的参数估计问题进行讨论具有重要的现实意义。
1 文献综述
生存分析中生存时间数据常常是截断和删失的,例如,在对某种类型的设备使用寿命进行的调查中发现,调查对象通常是使用寿命超过规定阈值的设备,而在调查前结束使用的设备和调查结束时仍在继续使用的设备并没有参与调查,得不到这些设备的具体使用寿命。因此,得到的样本是不完全的,即存在左截断和右删失,若仅用不完全样本直接进行分析显然不合适,故对左截断右删失数据进行特殊处理是十分必要的。
近几年,在截断和删失数据的基础上进行寿命分布的参数推断越来越普遍。例如,对于参数推断,Casella等[1]提出极大似然估计法是目前最流行的估计方法;Ahmadi等[2]假设在给定左截断右删失数据和生存时间随机变量时,比例风险模型会被简化,这种情况下能够得到未知参数的MLE和UMVUE(一致最小方差无偏估计),并详细给出了指数分布的点估计;胡江山等[3]研究了左截断右删失数据下泊松分布的贝叶斯估计,主要比较了极大似然估计和贝叶斯估计的有效性,证明了在小样本的情况下,贝叶斯估计比极大似然估计的精度要高,但在大样本时两者的精度相差不大,这也说明极大似然估计方法面对不完全数据的处理还是存在缺陷,故而Dempster等[4]针对不完全数据提出了EM(期望最大化)算法,通过引入潜在数据有效地进行统计推断。Shang等[5]在左截断右删失数据下进行广义伽马分布的估计时,基于EM算法改进后提出了EM算法的SEM(随机版本)作为计算近似极大似然估计的替代方法,并通过两种不同的方法获得迭代估计过程中的初始估计值,用Bootstrap(自助抽样)方法对广义伽马分布进行区间估计,最后运用蒙特卡洛模拟评估参数估计的优劣性;胡隽等[6]基于左截断右删失数据利用EM算法对指数分布进行参数估计,并通过实际数据证明所建立的似然函数能够得到收敛的参数估计值。此外,矩估计也是一种数值方法,具有良好的统计性质,在不完全数据类型下也有许多应用,如陈超等[7]提出使用矩估计的思想将参数估计问题转变成方程求解的问题,并证明了矩估计量的一致性和渐近正态性;Saulo等[8]给出双参数伽马分布的极大似然方法和矩估计量,并对三参数伽马分布模型的极大似然估计的二阶渐进性进行讨论;梁远胜等[9]针对非随机缺失的数据进行研究,使用矩估计方法对两参数伽马分布模型进行参数估计和分位数估计,也得到了很好的结果,但没有对伽马分布参数的置信区间做进一步讨论。
此外,关于左截断右删失数据下构造置信区间估计的研究中,Sauter等[10]提出基于参数向量MLE的渐近正态分布计算每个参数的近似置信区间;白永昕等[11]探究了左截断右删失数据中小样本时剩余寿命分位数的置信区间,并与传统构造置信区间的方法进行比较;Chen等[12]提出了伽马分布参数的闭式估计,其随着样本量的增加呈渐近正态分布,但这些估计的性能非常接近MLE。
鉴于此,基于左截断右删失数据选择矩估计方法对伽马分布参数进行推断,通过证明矩估计方法的渐近正态性质得到参数的渐近置信区间,并利用蒙特卡洛模拟对置信区间进行评价。
2 左截断右删失数据标识
寿命分析中左截断和右删失情况同时存在是常见的数据类型,忽略数据中的截断和删失会导致抽样误差,所以对于这类数据要进行一些特殊处理。左截断右删失数据的具体含义:在绝大多数生存分析的实验研究中,个体在进入研究前已经被诊断出患病称为左截断;在研究结束时感兴趣事件还没有发生或者在研究结束之前由于其他原因退出观察,这种情况被称为右删失。例如在某种疾病对个体生存时间影响的研究中,假设跟踪观察从2011年开始至2022年结束,共12年,感兴趣事件为在跟踪观察期间首次诊断出患有该疾病的个体到死亡或研究结束的生存时间,具体情况如图1所示。
患者1感兴趣事件在第2年初首次诊断出患病,第6年初死亡,其生存时间是可以正常观测到的;患者2感兴趣事件在第3年初首次诊断出患病,第9年初失踪,存在右删失;患者3感兴趣事件在第7年初首次诊断出患病,第12年初仍活着,存在右删失;患者4感兴趣事件在进入研究前就已经被诊断出患病,第12年后死亡,存在左截断右删失。这4位患者的生存时间分别为4,6+,5+,12+(年)。
3 左截断右删失数据下伽马分布的参数推断
3.1 基于矩估计左截断右删失数据下伽马分布的点估计
有h个服从Gamma(α,β)的样本Y=(y1,y2,…,yh)T,每个样本之间独立同分布,其密度函数和分布函数如下:
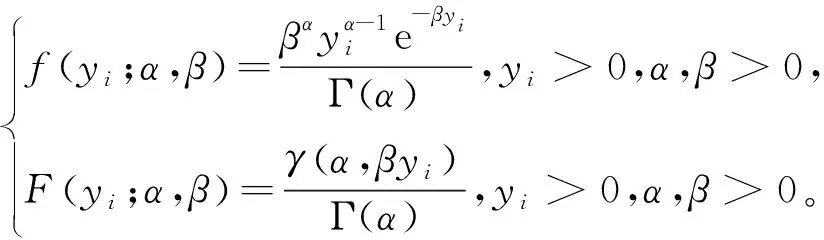
(1)
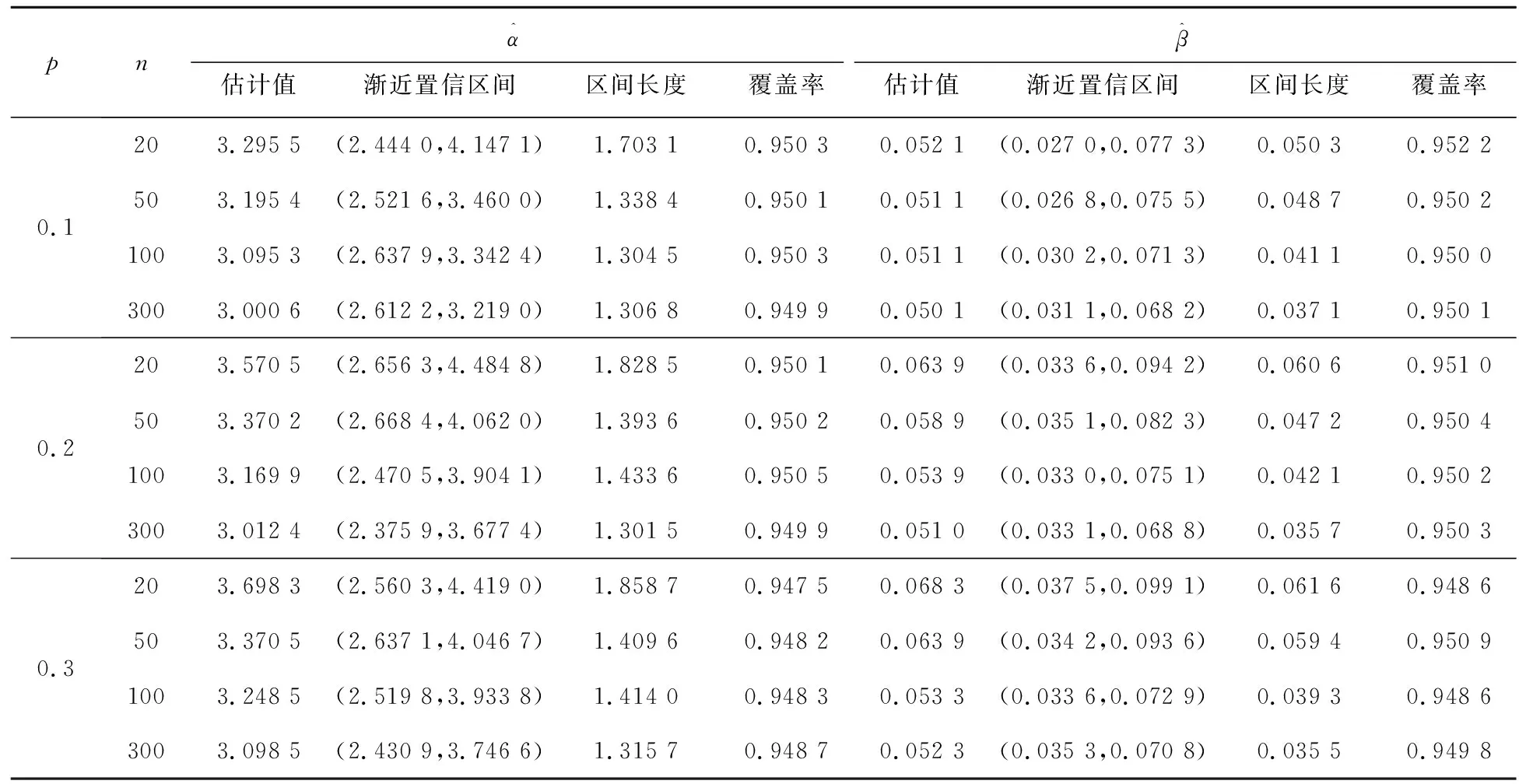
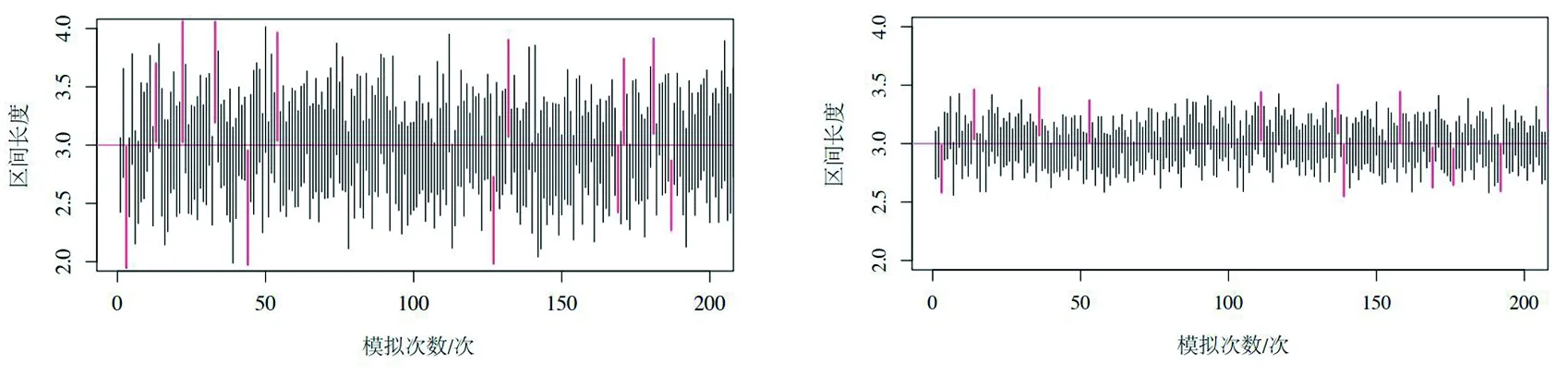
矩估计的主要思想是用样本的一阶和二阶原点矩去估计总体的一阶和二阶原点矩,得到参数α和β的估计值。将完全样本X=(x1,x2,…,xn)T中能观测到的数据记为Y=(y1,y2,…,yh)(h f(xi;α,β)=p·f(xi;α,β|δi=1)+ (1-p)·f(xi;α,β|δi=0), 其中p=P(δi=0)表示删失数据的比例。样本和总体的一阶原点矩和二阶原点矩分别为: (2) 如果数据不存在截断和删失,则得到参数数α和β的估计分别为: (3) 对来自条件分布的f(xi;α,β|δi=0)的右删失数据添加新的潜在数据Z=(z1,z2,…,zl)T,将观测数据和潜在数据整理成完整数据X=(Y,Z),用完整数据的样本一阶和二阶原点矩估计总体一阶原点矩μ1和二阶原点矩μ2: (4) 假设观测到yi的概率(删失机制)服从指数分布f(yi;λ)=1-exp(-yi/λ),λ是指数分布的参数,删失机制也可服从其他分布,但在指数分布下对于删失比例的调整更加灵活,应用到实际数据中适用性更强。记没有观测到yi的次数为η(yi),由于η(yi)是个随机变量,所以用期望代替。在给定观测值yi的条件下,η(yi)服从平移的几何分布: f(η(yi)=s|yi)=(1-f(yi,λ))sf(yi,λ), (5) 则有η(yi)期望为 E(η(yi)|yi)=(1-f(yi,λ))/f(yi,λ)。 对于观测数据Y=(y1,y2,…,yh)T(h f(zi,α,β|δi=0)= p=(λ/(β+λ))α。 (6) (7) (8) (9) (10) (11) (12) (13) 矩估计渐近正态性的证明是基于中心极限定理和Δ方法的。 定理1[13](中心极限定理) 设X1,X2,…,Xn是一组n维独立同分布的随机变量,记μ=EXi,Σ=covXiXj,i,j=1,2,…,n,i≠j,且Σ是正定的,则 (14) 进一步假设函数h(·)在点μ∈k的邻域内具有连续偏导数,以及Σ正定,用c表示h(·)在μ处的梯度向量: 则 (15) (16) (17) 式中: 证明假定θ=(α,β)T,则基于n个服从Gamma(α,β)的左截断右删失数据X的样本和总体的一阶、二阶原点矩分别为: (18) (19) (20) 且Σ正定,通过定理2得证。 (21) (22) 式中:za/2是标准正态分布上侧面积为a/2的z值。 为评价使用矩估计对左截断右删失数据下伽马分布的参数进行推断的合理性,基于上述理论依据式(9)—式(13)和式(21)—式(22),进行数值模拟试验。通过(6)式计算得到成功观测yi的概率λ,设定随机变量Y服从Gamma(3,0.05),X服从Gamma(2,0.05),删失比例p为0.1、0.2、0.3,完全数据的样本量n为20、50、100、300,将不同删失比例和样本量组合进行模拟,对于参数α和β、λ的初始值分别选择9、6、1,在迭代时两次参数估计值的差值小于设定的阈值0.000 1则停止迭代。在编写R语言代码时主要用到的函数有rgamma( )以及一些自定义函数。数值模拟结果见表1。 表1 不同样本量、删失比例情况的参数估计模拟结果 (a)n=20 (b)n=50 针对左截断右删失数据,在固定截断和删失时间点的情况下讨论了伽马分布的参数推断问题。引入潜在数据后利用矩估计方法建立完全样本一阶、二阶原点矩与总体一阶、二阶原点矩之间的关系,并通过证明矩估计方法的渐近正态性质得到伽马分布参数的渐近置信区间。数值模拟试验结果表明: 1) 固定完全数据的样本量时,通过比较不同删失比例下置信区间的长度和覆盖率发现:删失比例越小,需要引入潜在数据的个数就越少,参数估计结果会更接近参数真值,且置信区间长度也较短。 2) 固定删失比例时,通过比较不同完全数据的样本量下置信区间的长度和覆盖率发现:样本量越大,需要引入潜在数据的个数较多,由于矩估计方法适用于大样本情况,所以参数估计结果会更接近参数真值,且置信区间长度也较短。
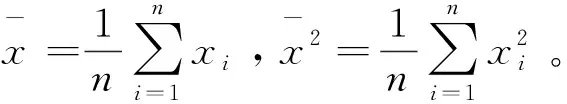

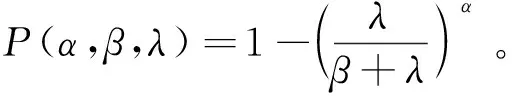
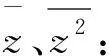
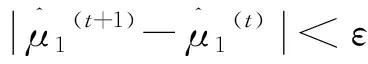
3.2 基于矩估计左截断右删失数据下伽马分布参数的渐近置信区间
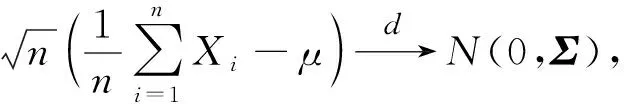

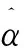



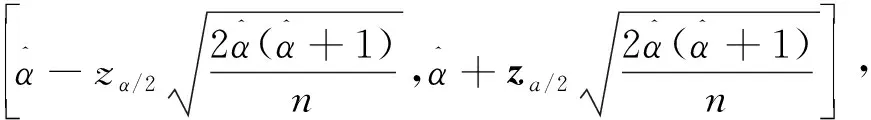
4 数值模拟
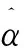
5 结论

