基于PID控制的精量播种仿真实验对比研究

姚兵，张策，王中義，陈年斌，王超

(山东理工大学 农业工程与食品科学学院，山东 淄博 255049)

伴随着我国农业信息化与智慧农业技术的发展,智能化精量播种方式取代地轮驱动的机械播种方式,成为未来的必然趋势[1]。由于传统的地轮驱动经常会出现打滑、偏移等现象,加上田间工作的环境十分复杂,从而会导致播种率降低,播种的均匀程度下降[2-5]。电机驱动的系统不仅可以使排种器转速稳定,提高播种率,还符合轻量化装备技术的发展趋势。凌琳[6]研究了一种玉米电驱精量播种区段控制系统,设计了基于增量式PID控制技术的排种驱动电机转速控制方法,实现对排种驱动电机转速的精准控制。雷小龙等[7]为避免地轮驱动排种会导致的许多负面影响,建立了一套优化PID的油菜播种控制算法,从而实现了油菜排种系统的控制精度与排种性能。刘思幸等[8]设计了一种基于卡尔曼滤波PID控制的精量排种器,卡尔曼滤波的引入对系统噪声干扰起到抑制作用,可提高系统稳定性,对电机精确控制及排种器精量播种起到了关键作用。丁幼春等[9]设计了一种油菜播种的导航控制器,并且基于免疫的PID算法完成对播种机的导航控制。Sidhu等[10]研究了一种控制系统,可以将排种器的工作转速与播种机前进速度相匹配,采用电机驱动的方式,减少地轮打滑带来的播种不均匀。Singhr等[11]研究了一种处理数据的微处理器与运行检测装置的系统,可以控制电机驱动排种器工作,在传动中加入减小摩擦的系统可以减少传递的扭矩,从而提高播种精度。

相比于传统的地轮驱动播种,通过电机控制来进行播种的方法不仅可以提高播种率,还可以节约成本。目前,PID控制技术已经受到广泛的关注,本文通过Simulink仿真对两种控制方法下电机输出的转速进行比较。

1 系统结构与工作原理

该电控系统主要由直流电机驱动模块、PIC18F258单片机、无刷直流电机、接线板以及CAN总线等组成,其原理图如图1所示。其中在电机驱动控制模块上的OUT1、OUT2端均为电机的电源控制端,ENA为控制电机输出的PWM控制端,IN1与IN2两端都设计为电机控制端的输出信号来直接决定被控制电机的转速大小。

图1 电控系统原理图

作业时,首先由底座上的测速传感器自动测得播种的作业速度,接收到CAN总线数据,根据串口屏参数由单片机直接计算出所驱动电机的目标转速,并且实时向驱动模块上发送输出PWM调制信号调整输入电压来控制输出电机的实际转速,通过PID控制算法将输出的电机目标转速与电机实际工作转速数据进行对比,并且继续调节PWM信号直至二者相同,完成播种作业。

2 播种电机选型

在实现精量播种的前提下,电机的选择对本次实验来讲十分重要,有别于传统地轮驱动的大豆植株播种机,本次实验电机的选型要根据大豆作物播种的具体要求而决定。经过查询相关数据得知,大豆植株在播种时一般种子最佳间距d约为10 cm左右,播种机车速v约为4 ～8 km/h,大豆玉米等植株排种器型孔数量x约为12孔,排种器所需要的扭矩T约为4 N·m左右。根据上述数据计算驱动电机的转速

(1)

根据电机转速的数值来计算电机所需要的实际功率

(2)

将大豆植株的相关数据代入式(1)和式(2),通过改变不同车速得出的电机功率见表1。为保证电机正常工作,电机最大功率要大于电机工作的实际功率。目前在农业中广泛使用的100 W专用播种施肥电机运行平稳、性能强、使用广泛,根据表1中功率数值来看,额定功率为100 W的电机可以保证播种正常工作;再根据选择的电机要具有调速简单、配合电机驱动模块使用时可以方便实现调速功能等特点,最终选择12 V 、100 W的永磁直流电机,该电机具有体积小、效率高、安装方便、噪声低等特点。

表1 不同车速对应功率数据表

3 传统PID控制算法

3.1 PID控制

PID控制是一种非常常见的控制算法,它将比例、积分、微分控制融合在一起,通过线性组合来重新定义系统量,并且用来控制被控对象,它包括位置式PID方法与增量式PID方法两种[12-13],如图2所示为系统原理图。

PID控制的微分方程为

(3)

式子中:e(t)表示控制的输入,即偏差值;u(t)表示控制的输出;Kp表示系统的比例系数;Ti表示积分时间常数;Td表示微分时间常数。系统输入一个值以后通过比例、积分、微分的调节进行响应的输出。比例控制可以控制整个系统的迅速反应误差,从而减小稳态的差值;积分控制可以很好地消除误差,积分控制器就是在不断地积累与输出控制量,直至误差为零,但是积分控制一旦出现过大情况,整个系统会出现明显的振荡,甚至有过大的超调量现象;微分控制恰巧相反,它可以预防振荡的出现,缓解超调现象使系统处于稳定状态,改善动态性能。PID控制器的传递函数为

(4)

在整套控制过程中,直流无刷电机是精量播种过程的核心部分,Simulink的仿真过程需要控制系统中的传递函数,因此必须研究直流无刷电机的传递函数。根据现代电机学原理得知三相直流无刷电机偏微分方程为[14]

(5)

式中:Td为电机电磁时间常数;Tm为输出机电时间常数;n1为电机转子相对转速;Ce为输入电动势系数;U0为反馈电压大小。对上述公式直接进行拉氏变换处理得到电机传递函数

(6)

电机的电磁时间常数表明电机在额定电压并且空载情况下,转速达到额定转速的63%时所需要的时间,该公式可以表示为

(7)

电机运行的机电时间常数也叫做机械时间常数,是指电机在连续空载启动情况下输出电流从最大值缓慢下降到其中值的63.2%时所消耗的时间,一般用来衡量电机的启动特性,该公式可以表示为

(8)

该套系统选用12 V 、100 W的永磁直流电机,相关参数代入式(7)、式(8)可得Td=0.01 s,Tm=0.978 s,Ce=0.075 V/(r·s-1),将这些数据代入式(6)中可以得出

(9)

在Simulink仿真中,式(9)称为被控对象传递函数,PID控制电控系统搭建的数学模型如图3所示。其中中间部分的Kp,Kd,Ki就是整个系统的三个参数,调整三个参数的数值可得出最优结果。

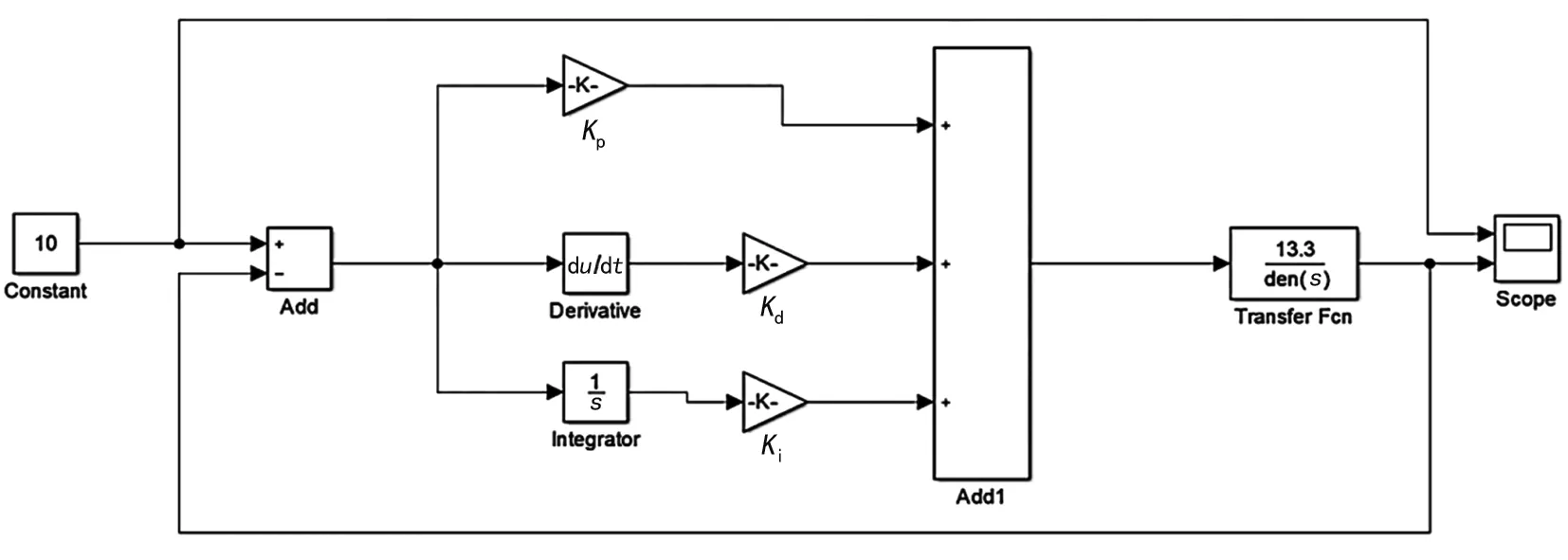
图3 Simulink数学模型

3.2 Z-N法调节PID控制参数

在PID控制的参数调整中,传统的控制方法为:第一步先调节比例,从中间值向两边值慢慢靠近,中间值的选取取决于此时电机的电压与电流;第二步将积分Ki的值从0逐渐增大,伴随着Ki的增大,直到找到一组系统稳态时间越来越短的图像,此时暂定一个积分Ki的数值;最后一步为调节微分Kd的值,也是从0逐渐增大,直到逼近目标值为止。但是普通的PID调节法虽然可以得到一组最优的参数组,但是随着机体的运动变化,整个系统也会随之发生变化,最优的参数也会有所差异,此时会出现偏差,故无法满足电机精量控制的需要;同时在上述步骤中寻找恰当的比例系数也是一步十分麻烦的操作,此时选取一种合适的方法进行参数调整变得尤为重要。

Z-N法是一种在工业领域内比较常见的反馈调节算法,这种方法大致分为两步:通过构建稳态闭合回路,确定稳态极限,即将Ki与Kd断开,然后调节Kp由低到高,直到图像出现一种稳态的等幅振荡为止,记录Kp的最小临界值Kpcrit与振荡周期Tcrit;对照Z-N公式表计算出另外两个Ki与Kd的数值,结果见表2。

表2 Z-N法参数计算公式

通过调节Kp的值发现,当Kp最小为1.5时,系统出现等幅振荡现象,此时Kpcirt的值为1.5,同时振荡周期Tcitr大约为0.7 s,将Kpcirt与Tcitr的数值代入到表2的Z-N法计算公式中,经计算此时的Kp为0.9,Ki为2.57,Kd为0.076,将计算出的三个值输入到模型中得出的图像如图4所示。图4中红色的横线表示电机的目标转速,绿色的线表示当前电机的实际转速,经对比发现系统当前电机转速仍存在较大范围的超调定值,并且系统目标响应时间范围约为2 s。为了方便进一步缩小系统超调控制量与系统的响应时间,在Z-N法计算结果的基础上继续进行简单有效的参数整体调整,调整后Kp为0.95,Kd为0.001,Ki为1.1,对应的系统响应曲线如图5所示。此时的系统响应时间大约为2.8 s,超调控制量很小。

图4 Z-N法参数计算响应曲线

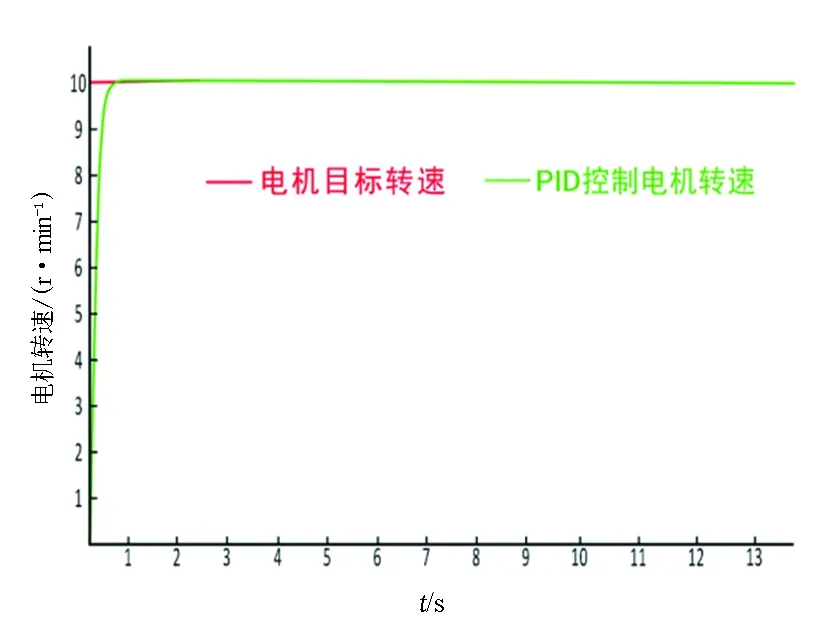
图5 Z-N法参数计算调整响应曲线

4 模糊PID控制算法

4.1 模糊PID控制原理

模糊PID控制[15]是将偏差e以及偏差的变化ec作为输入对象,利用预先设定的模糊控制规则对PID参数进行调整的一种控制算法。模糊PID控制算法首先要将变量模糊化,然后进行模糊推理得到模糊控制量,它实现的原理仍然是根据模糊控制器来自动调整PID控制的三个参数Kp,Ki,Kd的数值从而得到结果。模糊PID控制策略的原理图如图6所示。

图6 模糊PID控制原理图

4.2 模糊PID控制策略

在模糊控制器的实际工作中,输入的变量偏差e与偏差的变化ec经过量化与模糊化处理后要与变量论域相对应,然后进行模糊推理,根据模糊规则表的内容将所有规则输入到控制器当中,推理出参数整定变量值的dKp,dKi,dKd,其中变量值非对应线性关系如图7所示。

图7 变量值非对应线性关系

输入与输出的模糊子集为正大PB,正中PM,正小PS,零Z,负小NS,负中NM,负大NB, 根据模糊子集与所有模糊规则, 将三个参数的修正值通过解模糊过程变为准确值输入到PID控制器中从而实现PID的模糊控制。在模糊化与解模糊过程中都需要隶属度曲线,图8为输入变量e与输出变量Kp的隶属度曲线。

(a)e (b)Kp

5 PID控制与模糊PID控制对比

PID控制用途广泛、参数整定简单,且PID控制在简化的情况下可以变成基本线性且动态特性不随时间变化的系统;其次Ki与Kd的数值可以根据系统的波动及时进行调整,而且PID控制精度较高、原理简单、鲁棒性较强。

模糊PID控制是利用模糊逻辑及时对PID参数进行调整的一种算法,它根据模糊控制器中的模糊规则对参数及时修定,克服了普通PID控制有时无法实时调整参数的缺点,模糊PID包括确认模糊化、模糊推理、创建模糊规则、解模糊等步骤来最终确定参数数值。但模糊PID一个最大的缺陷在于将参数进行模糊处理时很可能会导致系统鲁棒性降低、动态属性变差。

在本次仿真实验中,对电机传递函数的PID控制与模糊PID控制进行了仿真对比,为了更好比较,均输入相同的参数值,得到的系统响应曲线对比结果如图9所示,图10为系统响应对比局部放大图。不难看出,在Kp,Ki,Kd参数值相同的条件下,传统PID控制下系统达到稳态响应的时间与模糊PID控制下系统达到稳态响应的时间有所差异,且系统超调量也有细微的差异。

图10 系统响应曲线对比结果局部放大图

6 结论

1)当电机目标转速一定时,常规PID控制下,转速超调量最大在0.5 s处,转速超调大约为0.66%,系统调节时间约为2.8 s;模糊PID控制下,转速超调量最大在1.25 s处,转速超调大约为0.80%,系统调节时间约为6.5 s。对比说明在PID控制下系统超调量低、调节时间短、稳态误差有所减小,系统鲁棒性更强。

2)在PID控制下驱动电机达到稳态的时间优于在模糊PID控制下的时间,可以使电机转速快速精准地跟随作业目标转速,达到预期目标,在相同时间内种子粒距均匀指数会更高,因此采用PID控制算法更利于实现精量播种作业。