斜风下斜拉-悬吊组合体系桥静风稳定性研究
张新军,胡智勇,孙雷雷
(浙江工业大学 土木工程学院,浙江 杭州 310023)
斜拉-悬吊组合体系桥是将传统悬索桥和斜拉桥融合于一体的一种缆索承重桥梁结构形式,具有跨越能力强、结构刚度大、结构动力性能好以及造价低等特点[1]。研究表明:斜拉-悬吊组合体系桥在1 100~1 800 m跨径范围内可以与悬索桥竞争,尤其在1 400~1 800 m跨径范围内更具有优势[2]。自1883年建成纽约布鲁克林大桥以来,斜拉-悬吊组合体系桥经过140年的研究实践,罗勃林、狄辛格、斯坦因曼、林同炎和吉姆辛等相继提出了各自的结构体系,并在多座世界大跨桥梁的方案设计中采用[1-2]。斜拉-悬吊组合体系桥在实际工程中得到成功应用,如2016年建成通车的土耳其博斯普鲁斯海峡三桥(主跨1 408 m)和我国在建的西堠门公铁两用大桥(主跨1 488 m)等。作为一种新型缆索支承桥梁,斜拉-悬吊组合体系桥跨度大,结构轻柔,静风稳定性是其建设需要考虑的关键问题。近年来,国内外学者虽然围绕斜拉-悬吊组合体系桥的结构体系、静力和动力性能等问题开展了众多的研究[2-8],但很少涉及静风稳定性的研究。张新军等[9]针对主跨1 400 m的吊拉组合体系桥,采用三维非线性静风稳定性分析方法,开展了两种主梁架设顺序全过程的静风稳定性分析。邵国攀[10]拟定主跨2 100 m超大跨度吊拉组合桥梁方案,采用基于ANSYS的非线性静风响应分析程序对主梁采用整体钢箱梁和分体双箱梁两个设计方案的静风稳定性进行对比分析。杨进[11]针对主跨1 488 m的斜拉-悬索协作体系桥梁开展非平稳风场作用下的静风和抖振响应分析,并揭示了静风响应对非平稳抖振响应的影响。上述斜拉-悬吊组合体系桥的静风性能研究都是基于法向风作用情形,即假定风垂直地吹向桥轴线。大跨度桥梁的桥位设计和现场风速观测均表明桥梁所受强风的来流方向大多偏离桥跨法向[12],因此开展斜风作用下结构的静风稳定性研究更具实际工程意义。当前,虽然针对斜风作用下斜拉桥和悬索桥的静风性能已开展了数值分析和试验研究[13-16],但对于斜拉-悬吊组合体系桥至今未见文献报道。
为此,采用考虑静风荷载和结构非线性的斜风作用下结构三维非线性静风分析程序,针对主跨1 400 m的斜拉-悬吊组合体系桥设计方案进行法向风和斜风作用下结构的静风稳定性进行分析,并揭示斜风作用对斜拉-悬吊组合体系桥静风稳定性的影响,为该类桥梁的抗风分析提供理论指导。
1 斜风作用下结构三维非线性静风稳定性分析程序
当前,斜风分析主要有斜风分解法和斜截面法等两种方法[12]。前者将斜风分解为垂直和平行于桥跨方向的两个分量,并分别计算顺桥向和横桥向的静风荷载,最后将静风荷载施加到结构上进行分析[3]。这是一种近似的处理方法,虽然比较适用于跨度不大的闭口扁平箱形主梁断面,但是对于开口或开槽的主梁断面,由于横梁暴露引起的挡风效应会导致偏于不安全的计算结果。后者直接采用风洞试验中测得的斜片条节段的静风荷载六分力系数计算静风荷载及其响应,该方法准确地考虑斜风作用对结构静风响应的影响,笔者分析就采用该方法。斜风作用下斜拉-悬吊协作体系桥的静风稳定性分析采用斜风作用下结构三维非线性静风稳定性分析程序(以下简称3DNASA-SW),其流程如图1所示[17]。3DNASA-SW基于斜风作用下主梁和缆索单元的静风荷载计算模型,考虑结构及其所受静风荷载的双重非线性特性及三维效应,通过外层风速增量和内层静风平衡状态迭代的增量迭代方法搜寻结构的静风失稳临界状态。计算程序中的结构三维几何非线性分析采用CR(Co-rotational)-UL(Updated lagrangian)方法,即拖动坐标修正拉格朗日法,以有效处理大跨度桥梁结构的大位移和大转动问题。
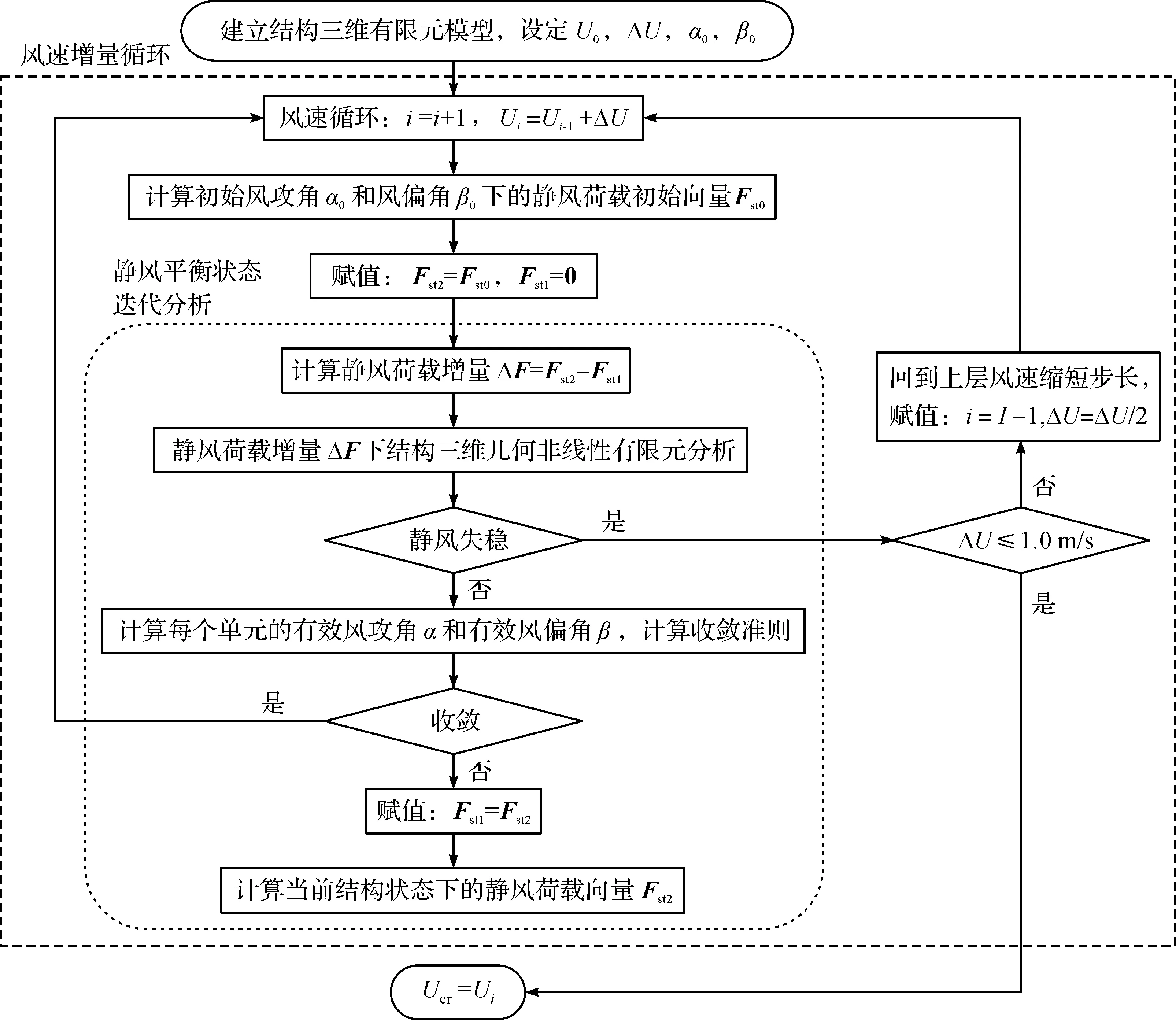
图1 3DNASA-SW流程图
2 桥梁及三维有限元模型简介
图2为一座1 400 m主跨的斜拉-悬吊组合体系桥设计方案,两个边跨各为319 m。主跨由618 m的悬吊段、680 m的斜拉段以及两侧各54 m的斜拉悬吊结合部组成,每个结合部设置4对交叉吊杆。主缆横向间距34 m,吊杆间距18 m,悬吊段主缆矢跨比为1/10。斜拉索在边跨和中跨的锚固间距分别为14 m和18 m。桥面主梁采用闭口钢箱梁,宽36.8 m,高3.85 m。桥塔为钢筋混凝土门式框架结构,塔高约259 m。锚碇为重力式锚碇。

图2 斜拉-悬吊组合体系桥设计方案(单位:m)
以下分析时将图2简化为如图3所示的三维有限元分析模型,当中桥面主梁、桥塔及刚性横梁均采用空间梁单元模拟,主缆、吊杆及斜拉索则采用空间杆单元模拟。桥面主梁采用鱼骨式计算模型,主梁与吊索和斜拉索之间通过刚性横梁进行连接。塔梁之间耦合横向自由度,墩梁之间耦合竖向和横向自由度。
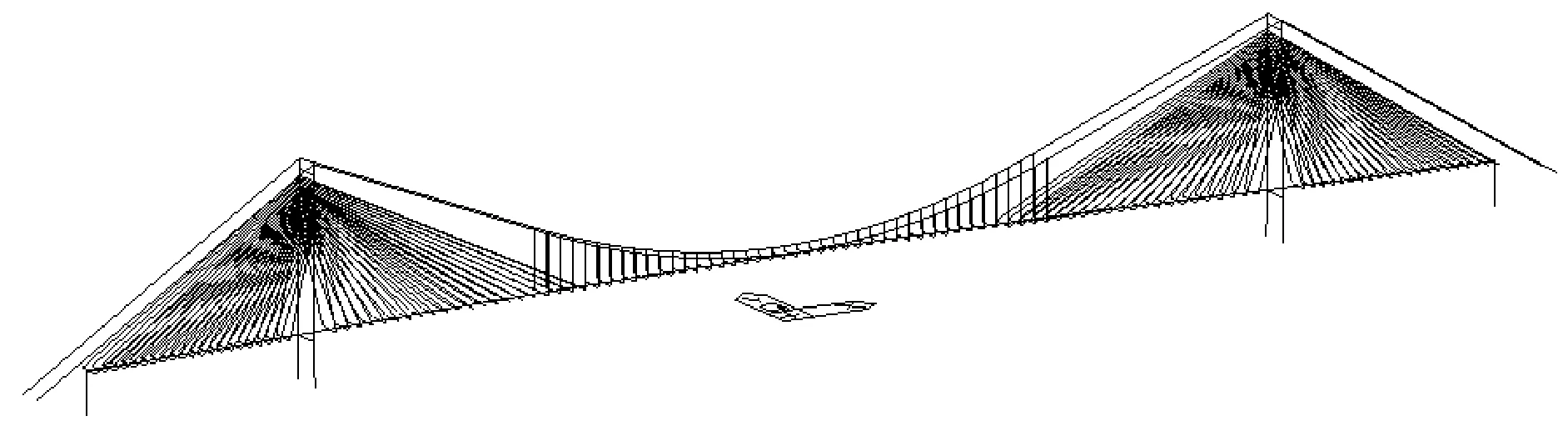
图3 斜拉-悬吊组合体系桥三维有限元分析模型
3 斜风作用下斜拉-悬吊组合体系桥静风稳定性分析
采用与方案桥主梁断面形状和尺寸极为相似的类似主梁(图4)在斜风作用下节段模型风洞试验测得的静风六分力系数(图5)[18],基于方案桥成桥阶段三维有限元模型,在-3°~3°初始风攻角和0°~20°初始风偏角范围内,采用3DNASA-SW分析了该桥的静风稳定性。由于其余方向的静风位移都很小,图6中仅给出主跨跨中处主梁横向、竖向和扭转位移随风速增加的变化曲线。图6中:β0为初始风偏角;DL为横桥向位移;DV为竖向位移;DT为扭转角。
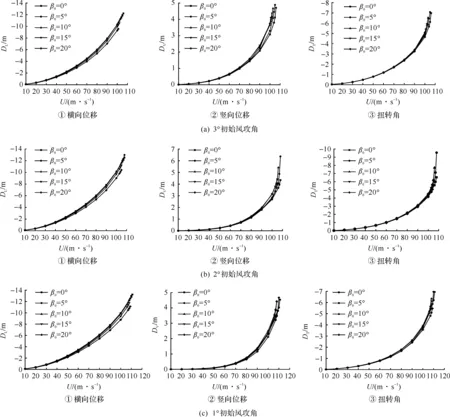
图6 主梁跨中位移随风速增加的变化规律
由图6可知:1) 在法向风(β0=0°)和斜风(β0≠0°)作用下,主梁横桥向、竖向和扭转位移随风速的增大呈非线性增长趋势,风速增大到一定程度后主梁的竖向和扭转位移会突然增大,当达到临界风速后,主梁位移出现发散现象而导致结构丧失稳定性。斜拉-悬吊组合体系桥的静风失稳形态是一种主要由主梁竖弯和扭转耦合失稳的形态,与法向风作用下的静风失稳形态相同,表明斜风作用并不会改变斜拉-悬吊组合体系桥的静风失稳形态,然而会显著影响其静风失稳临界风速。2) 不同初始风攻角下,主梁跨中处位移的演变规律略有不同,在负的初始风攻角下,当风速增大到一定程度后,主梁的竖向和扭转位移变化曲线存在明显拐点,呈现出“硬”静风失稳特点,而在0°和正初始风攻角下则没有明显拐点,表现为“软”静风失稳特点。
为了清楚地了解斜风作用对斜拉-悬吊组合体系桥的静风稳定性的影响,图7给出了不同初始风攻角下静风失稳临界风速随风偏角增加的变化趋势。图7中:实线表示3DNASA-SW计算结果;虚线表示斜风分解法的计算结果;两者之间的差异率γ如表1所示,计算式为

表1 程序和斜风分解法计算结果的差异率

图7 不同风攻角下静风失稳临界风速随风偏角增加的变化趋势
γ=(Ucr,procedure-Ucr,decomp)/Ucr,procedure
(1)
式中:Ucr,procedure为3DSNAA-SW计算的静风失稳临界风速;Ucr,decomp为斜风分解法得到的静风失稳临界风速,其计算式为
Ucr,decomp=Ucr,0°/cosβ0
(2)
式中Ucr,0°为法向风(β0=0°)下由3DSNAA-SW计算的静风失稳临界风速。
由图7可知:不同初始风攻角下静风失稳临界风速随风偏角增大的变化趋势各不相同,在-2°和-3°初始风攻角下呈现单调递增趋势,在1°、2°和3°初始风攻角下则呈逐渐下降趋势,而在-2°和-3°初始风攻角下,则呈现先下降而后缓慢增加的变化规律。因此,除-2°和-3°初始风攻角外,其余风攻角下的静风失稳临界风速均出现在风偏角为10°(0°、1°和-1°风攻角)、15°(2°风攻角)和20°(3°风攻角)的斜风情况下。在所计算的风攻角和风偏角范围内,该方案桥的最小静风失稳临界风速为101 m/s,出现在3°风攻角和20°风偏角情况。因此,为确保桥梁结构的抗风安全性,应重视斜风作用下的静风稳定性分析。另外,如图7所示,各初始风攻角下程序计算得到的静风失稳临界风速随风偏角增大的变化规律并非如斜风分解法所分析的余弦变化规律。由表1可知:程序和斜风分解法计算结果的差异率为-11.7%~2.9%,且随着风偏角的增加两者之间的差异显著增大。除-3°风攻角外,其余风攻角下的程序计算结果均明显小于斜风分解法计算结果,采用斜风分解法会高估结构的静风稳定性。因此,为准确预测桥梁的静风稳定性必须采用考虑斜风作用、静风荷载和结构非线性的斜风作用下结构三维非线性静风分析方法。
为了揭示斜风作用对斜拉-悬吊组合体系桥静风稳定性的影响程度,定义斜风作用对静风失稳临界风速的影响率ηβ为
ηβ=(Ucr,β0-Ucr,0°)/Ucr,0°
(3)
式中Ucr,β0为初始风偏角β0下的静风失稳临界风速。各初始风攻角和风偏角下斜风作用对方案桥静风失稳临界风速的影响率如表2所示。

表2 斜风作用对静风失稳临界风速的影响率
由表2可知:斜风作用对斜拉-悬索组合体系桥静风稳定性的影响存在正负效应,在非负风攻角下斜风效应将降低结构的静风稳定性,而在负攻角下则会提高静风稳定性,影响率为-4.7%~9.5%,不同初始风攻角下的平均影响率为-3.1%~4.6%。同时,斜风作用对静风失稳临界风速的影响随着初始风偏角的增加逐渐显著,因此需要特别关注非负攻角下较大风偏角的斜风对斜拉-悬索组合体系桥静风稳定性的不利影响。
4 结 论
采用3DNASA-SW,以1 400 m主跨的斜拉-悬吊组合体系桥设计方案为研究对象,进行了法向风和斜风作用下的静风稳定性分析,研究结果表明:1) 斜拉-悬吊组合体系桥的静风失稳表现为主梁竖向弯曲和扭转强烈耦合的失稳形态,斜风作用不会改变斜拉-悬吊组合体系桥的静风失稳形态。不同初始风攻角下的结构静风失稳现象有所不同,呈现出“硬”或“软”的静风失稳特点。2) 不同初始风攻角下斜拉-悬吊组合体系桥静风失稳临界风速虽然随风偏角增大的变化趋势各不相同,但都不是如斜风分解法所述的余弦变化规律,最小静风失稳临界风速大多出现在斜风作用情况。程序分析与斜风分解法计算结果的差异率为-11.7%~2.9%,且以负值为主。除-3°风攻角外,程序计算结果均明显小于斜风分解法计算结果,斜风分解法将高估斜拉-悬吊组合体系桥的静风稳定性。3) 斜风作用对斜拉-悬索组合体系桥的静风稳定性存在着正负影响,影响率为-4.7%~9.5%,尤其要注意非负攻角下较大风偏角斜风的不利影响。为准确预测斜拉-悬吊组合体系桥的静风稳定性,必须采用考虑静风荷载和结构非线性的斜风作用下结构三维非线性静风分析方法。

