同态加密技术在大数据安全中的应用研究

秦宏春

(中国人民解放军 758471部队,湖南 长沙 410007)

0 引言

由于近几年物联网传感技术与移动互联网的快速发展以及在全世界的迅速普及,导致大量的数据信息被记录并上载到网络。这些数据信息拥有规模巨大、结构复杂、价值密度低等特点。因此,如何从这些关联性弱、碎片化的大数据集合中获取具有商业价值的信息,是目前行业研究的热点。但在大数据挖掘带来各种社会便利的同时,也不可避免地存在大数据泄露个人隐私等安全问题。与传统的数据隐私保护不同,大数据除了要防止存储阶段的泄露,还要防止计算阶段的隐私泄露问题。如何兼顾保证大数据可以被保密存储并被安全利用的同时不被恶意第三方获取,是大数据隐私保护要面对的核心问题。

1 大数据不同阶段下的安全问题

信息化时代,传统的数据面临着诸多的安全问题,如计算机系统自身的局限性与外部的恶意攻击。而新型大数据与传统数据的全流程都不尽相同,因此需要考虑的安全问题也有一定的差异。在分析大数据安全问题时,需要根据大数据的生命周期来分类。

在大数据的整个生命周期内,主要在于存储、搜索和计算3个阶段可能面临隐私泄露的问题。这是因为大数据集拥有数据规模大的特点,一般的数据拥有者很难与传统模式一样将大数据存储在本地,而不得不存储在云服务器上。同样由于数据的总量庞大,导致个人没有足够的算力完成大数据检索或计算,因此往往需要将数据外包给第三方处理。但在实际环境中,无论是云服务存储者还是第三方数据处理者都不是完全可信的,数据拥有者既要保证数据以密文存储从而防止信息泄露,又要使得处理者可以顺利计算。

1.1 大数据存储阶段

由于大数据拥有者往往将大数据存储在云端,因此为了防止数据泄露,用户需要对数据进行加密处理。而大数据量庞大且近指数级增长,所以如果选择的加密算法效率低下,不但会消耗大量的加密时间,还会导致数据密文严重膨胀,占据过量云存储空间[1]。同时,大数据结构复杂,稳健性较低的加密方案极易导致数据错位和存储混乱,不利于数据的后期处理与管理。

1.2 大数据搜索阶段

大数据搜索主要是针对密文存储形式的大数据完成基于关键词、短语或正则表达式的查询和检索操作。因此,该阶段的处理方式需要加密方案有良好的功能性,即加密后的密文有一定的抗碰撞性。尤其是在面对海量的数据集时,这样的抗碰撞性既要使得密文可搜索又要拥有选择明文攻击下的不可区分性[2]。

1.3 大数据计算阶段

用户将大数据计算外包给第三方计算服务者时,往往希望第三方能在不破坏加密性的前提下完成相关计算。而大数据计算不但有着计算量庞大还有着计算方式复杂多样等特点。该阶段必须选择一个具有密文可计算功能的隐私保护方案,并在计算的复杂度和计算方式上更为全面[3]。综上所述,相比于传统的数据模式,大数据各阶段需要面对更多种的数据处理方式,这些处理方式与安全问题紧密相关,如果选择的加密方案不当,会导致处理效率低下且容易导致数据受损甚至泄露。因此,本文接下来将分析基于同态加密的解决方案。

2 同态加密解决方案

加密是保护任何敏感信息隐私的关键机制,然而,传统的加密方案在没有解密的情况下不能对加密数据进行操作。换句话说,用户不得不牺牲他们的隐私来使用云服务,如文件存储、共享和协作。此外,不受信任的服务器、提供商和云运营商可以在用户结束与服务器的连接后,很长时间内保持对用户元素的物理识别。而同态加密这种特殊的加密方案可以解决一系列的问题,因为它的原理特性允许第三方对加密数据进行操作,而无须事先解密。假设明文为M={T1,T2…Tn};密文为C={c1,c2…cn};加密函数为E;解密函数为D;评估函数为f,则在同态加密中以下式子一定为真:E(f(T1,T2····Tn))=f(E(T1),E(T2)····E(Tn))。即经过同态加密之后,如果对密文进行操作,解密之后的明文也会有对应的效果。这样的特性使得用户可以安全地将数据交于第三方处理,在转移了计算成本的同时又保护了个人的隐私,如图1所示。

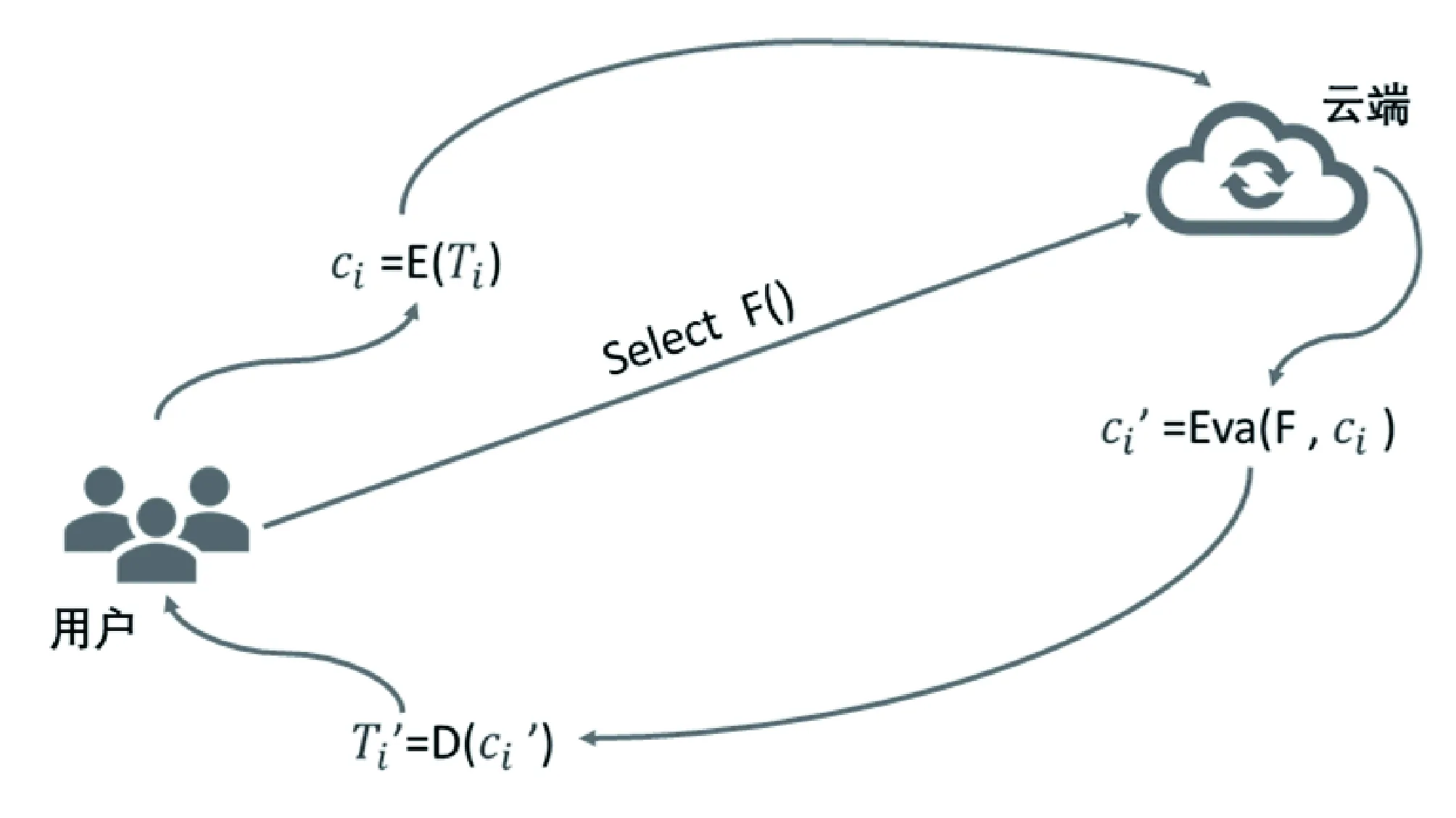
图1 同态加密

同态加密根据同态性的程度可以分为3类,分别是部分同态加密、某种同态加密和完全同态加密。下面将介绍3类同态加密下的具体加密算法原理以及其算法性能。

2.1 部分同态加密

部分同态加密算法只允许一种类型的操作,比如加法或者乘法,但是使用的次数不受限制。由于同态操作的类型限制,只能作用于特定的应用,如电子投票和信息检索。

2.1.1 RSA算法

RSA算法实现了乘法同态[4]。RSA的安全性基于两个大素数乘积的因式分解问题的困难性。目前已经分解的最大整数232位十进制,768位二进制。而整数分解问题主要的破解方法是暴力破解,即穷举素数相乘的结果。RSA作为较为早期的加密算法之一,应用广泛,但是缺点在于密钥尺寸大、加密解密速度慢。在计算机运算能力越来越强的今天,RSA变得非常不安全。

2.1.2 GM加密系统

GM加密系统实现了加法同态,其安全性主要是基于二次剩余难以复合困难性问题。但它不是一种有效的密码系统,因为它的密文膨胀系数过大,可能会导致密文比原始明文大数百倍。

2.1.3 El-Gamal加密系统

El-Gamal加密系统实现了乘法同态,是一种基于Diffie-Hellman密钥交换的用于公钥密码学的非对称密钥加密算法。该算法的缺点在于密文的一般扩展大小为1∶2,对于空间敏感型的系统不太友好。

2.1.4 Paillier

Paillier满足同态加以外还满足以下操作[5]:(E(m1)m2modn2)=m1m2modn,D(E(m1)E(m2)modn2)=(m1+m2)modn。Paillier加密基于一种新的基于复合剩余问题的概率加密方案,区别于其他的同态加密算法,其独有的附加同态属性描述了加密数据和明文上的各种操作之间的不同交叉关系,也给予了使用者更多的可能。

2.1.5 GM 加密系统的衍生

加密数据的任何乘法运算都对应于明文上的加法运算,即加法同态。是对GM加密系统的改进,同样也是基于高剩余性问题。具体细节差异在于加密的信息不再是一个比特一个比特而是以块为单位加密,以此提高了加密性能。

2.1.6 Okamoto-Uchiyama

该团队提出了一种新的部分同态加密算法,主要思路是通过改变以前HE方案的集合而改进计算性能。还有其他大量的工作是对经典同态加密算法的改进,旨在提高计算效率、时间空间开销。

部分同态加密是最早也是较为成熟的加密技术。上述所列举的算法中,RSA与Paillier的运用最为广泛。虽然大部分的同态加密只能实现加法或者乘法同态性,但是在性质与性能中达到了较好的平衡。

2.2 某种同态加密

某种同态加密允许有限次数的某些类型的操作,属于不完全的同态方案,密文的大小随着每个同态操作而增长,因此允许的同态操作的最大数量是有限的。

(1)BGN是一种同态加密方案[6],是Boneh等在2005提出的一种具有全同态性质的加密方案。和传统的仅能支持单同态的El-gamal和Paillier加密方案不一样,BGN能够同时支持任意次数的加同态单,但只支持一次乘同态运算。由于乘法同态的实现是通过双线性对性质实现的,所以只能实现一次的乘同态。

(2)其他方案:除去BGN还有多种其他类似的方案,但是大多效果不完全。比如Polly Cracke允许密文进行乘法和加法运算。但是运算的密文大小随着同态运算呈指数增长,乘法运算的开销极其昂贵。后续还有变种的算法提出,但是这些方案要么不安全要么不切实际。比如Albrecht介绍了一个带有噪声的波利破解密码系统,其中同态加法运算不增加密文大小而乘法使得密文大小平方倍增长。

总的来说,某种同态加密是人们在研究完全同态加密过程中的产物。虽然能实现不改变密文大小且次数不限的同态加法,但是乘法往往会受到严格的限制,无论是次数还是密文存储都是不理想的。在实际应用中一般不会采用某种同态加密,为了残缺的乘法同态舍弃性能是得不偿失的。

2.3 完全同态加密

在引入隐私同态概念近30年后,Gentry等[7]终于提出第一个完全同态加密方案。尽管这个方案只是理论性的,而且是不可实现的。但是在后续许多学者在这个理论基础之上利用许多密码假设进行了实例化,设计了越来越多更简单且更有效的加密方案。目前主要有3个完全同态加密方案,分别是基于理想格、基于整数以及基于误差学习。

2.3.1 基于理想格的同态加密

2011年,Gentry等[8]在他人的工作基础之上通过优化密钥生成和应用批处理技术,终于实现了Gentry初始方案的变体形式G09,这也是完全同态加密的第一次实现。然而,如同原始方案中的缺点一样,其计算开销极其庞大。公钥大小为2.3 GB,生成密钥需要2.2 h,加密一条消息需要3 min,而刷新密文需要30 min。它依赖于多种新型且未经测试的复杂性假设。

2.3.2 基于整数的同态加密

Dijk等[9]没有选择理想格,而是使用了基于整数构建了同态加密。该方案主要优点在于概念简单,然而该方法依旧不实用,因为产生的公钥庞大且加密效率低下。即使在后人优化之后,也还会生成大小为802 MB的公钥,生成密钥需要43 min,加密消息需要2 min7 s,刷新密文需要3 min 55 s。

2.3.3 基于误差学习的同态加密

为了将FHE方案建立在经过充分研究的数学问题的基础上,Brakerski 以及Vaikuntanathanz证明了第一个偏离Gentry计划的FHE方案[10]。这种新型的FHE方案基于标准的LWE假设,通过引入一种叫做重新线性化的技术,避免了理想格上未经测试的假设。此外,应用了一种叫做降维模数的技术来避免Gentry方案中不可或缺的挤压过程,从而阻止了涉及SSSA问题。但是这种方案依旧不是完美的,必须依赖于开销巨大的自举,从而开销巨大。

综上所述,Paillier方案是在加密效率、密文膨胀度以及安全性等指标中综合性能最优并且运用范围最广的。尽管Paillier方案只能实现加法同态性,但该方案依旧是大数据计算阶段隐私安全保护最有效的措施之一。

3 结语

同态加密方案的明密文计算同态特质可以有效解决大数据计算中隐私保护的问题,但是目前广泛运用的同态加密往往是部分同态加密,只能完成加法或者乘法同态。针对大数据的计算方式复杂等特性,全同态加密则是最能平衡安全性和可计算性的方案。现有全同态加密技术的运行效率、密文膨胀程度和安全性仍没有达到实际可运用的程度。因此,设计高效率和低成本的完全同态加密算法,并运用在大数据安全之中,是一个重要的研究方向。