以学定教,让数学学习真正发生
梅升
[摘 要] 建构主义学习理论提出:学习者在原有认知经验的基础上生发出新的知识,是学习真正发生的过程. 因此教师设计教学时,需充分了解学生的原有认知结构,以学定教,让知识自然生成. 文章以“向量的加法”的教学设计与评析为例,提出:尊重个体差异是“以学定教”的前提;教师精心预设是“以学定教”的关键;发展核心素养是“以学定教”的目标.
[关键词] 以学定教;个体差异;精心预设
“以学定教”是指根据学情确定教学方案. 学情包括学生的知识与技能基础、现有的认知水平、对新知的情绪等;定教是指在合适的起点选择最优的教学手段,促进学生的发展. 在教学中,囿于课堂时间与空间的限制,“生成知识”需耗费较多的时间,有些教师就选择奉送概念、直给结论等方式缩短教学时间. 这种忽视知识形成过程的教学方法,严重阻碍了学生思维的发展.
俗话说“磨刀不误砍柴工”,想让学习真正发生,就要在“以学定教”的基础上实现知识的“再创造”. 本文以“向量的加法”的教学设计与评析为例,提出“以学定教”的前提、关键和目标,与君共勉!
教学设计与评析
第一个环节:情境导入
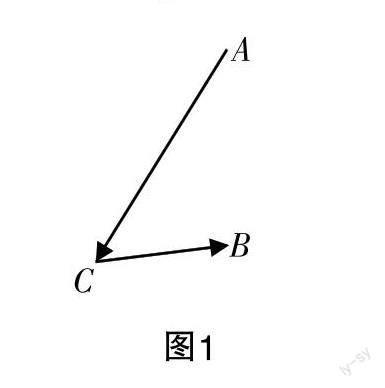
情境1 如图1所示,机场A没有直达机场B的航班,若想到机场B需从机场A出发经机场C转机,该如何设计飞行航线呢?
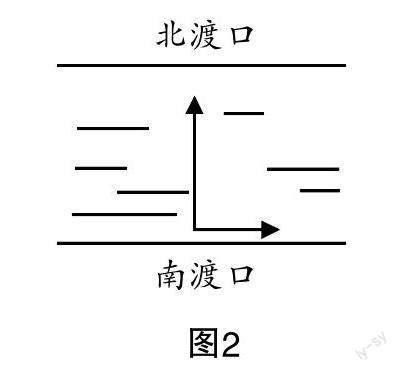
情境2 如图2所示,已知长江江水向东流动的速度为12.5 km/h,若渡船的船速为25 km/h,该渡船想要垂直地从长江南渡口开到长江北渡口,该怎么确定其航向?
问题1 在两幅图(图1、图2)中分别画出两次位移的合成与速度的合成,如果将它们视为向量,分析三者间具有怎样的关系.
问题2 如何用数学符号表达它们的关系?
问题3 填空:①已知非零向量a,b,在平面内____,作____,____,那么向量____叫做a与b的和,写作____. 求两个向量和的运算,叫做____;②a+0=( );③a+(-a)=( ).
问题4 写出向量的加法法则.
问题5 说说向量加法中的平行四边形法则与三角形法则的区别与联系.
评析 两个情境都源于学生熟悉的现实生活,且与物理学科中的“矢量的合成”有着异曲同工之妙,不仅成功吸引住了学生的注意力,让学生对向量的加法产生了探索欲,还从一定程度上实现了学科间的关联,让学生感知物理与数学学科之间的联系,为后续深入探讨“如何加向量”奠定了基础.
纵观上述几个问题的设计,前两个问题(问题1和问题2)主要引发学生在观察中对向量的加法产生直观感知与体验,并尝试将这种体验用数学语言表达出来;问题3、问题4属于对向量加法的概念与方法的归纳过程,这也是对数学知识进行规范表达与提炼的过程,意在引导学生学会用规范的数学语言对向量的加法加以概括;问题5意在引导学生对向量加法中平行四边形法则与三角形法则进行类比,发现这两种向量加法法则在本质上属于“异途同归”,而且平行四边形法则还可以转化成三角形法则,从而揭示向量加法法则的本质规律,学生的思维也在类比思想的应用中得以有效发展.
第二个环节:尝试体验
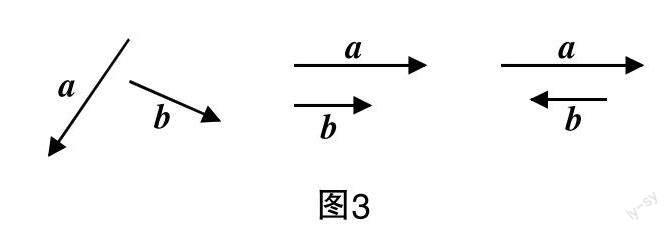
向量a与b如图3所示,作出向量a+b.
评析 充分了解学情是“以学定教”的前提. 在探究前,学生的认知水平究竟处于什么样的层次?是否具备一定的潜能,能独立思考并解决一些问题?这些都是客观判断学情的基本条件,也是进行教学安排的依据. 在情境导入时,虽让学生对向量加法法则进行了提炼与总结,但学生理解与掌握的程度究竟如何?是表浅记忆,还是真正理解了向量加法法则呢?这些都需要通过检验才知晓.
尝试体验环节能让教师洞察出学生是否真正了解了向量加法中“首尾相接”的内涵,當遇到没有平行四边形与三角形作为背景依托时,两个向量处于共线状态该如何作出“和向量”?若学生的思维出现了卡壳状态,则教师可通过适当点拨为学生指点迷津. 如引导学生将目光回归到向量加法的概念中来,根据首尾相连与起点指向终点的特征来分析并解决问题.
因此,这是一个引发学生产生主动思考的环节. 看似简单的一个问题,却蕴含着大能量,学生通过主动思考、探索与尝试,将原本浮于表面的认识逐渐内化到认知体系中,形成深度思考. 随着问题的解决,不少学生从中探寻出了重要的通性通法,并在知识的本质中摸索到了重要规律.
当然,若学生在此环节中出现了思维障碍与错误解法,教师可通过适当点拨,帮助学生调整解题思路,并在思维冲突中进一步深化对向量加法法则的认识.
第三个环节:探究释疑
探究1 如图4所示,请用作图法来验证向量a,b,c的加法交换律与结合律.
探究2 (1)如图5①所示,求+++;(2)如图5②所示,求同一平面内n(n>3)个向量的和.
探究3 如图5③所示,若将同一平面内的n个向量首尾相连,形成封闭的折线,求这n个向量的和.
评析 新课标明确提出:有效的数学学习活动不能单纯的依赖模仿与记忆,动手实践、自主探究与合作交流是学生学习数学的重要方式. 数学学习需要主动性,而探究过程则是体现学生为课堂的主人,发挥其学习主动性的重要契机.
探索作为教学活动的重要环节,是培养学生实践能力与创新意识的主要途径,也是促使学生形成深度学习的载体,对提升学生的学习能力与思维能力具有重要影响. 观察上述三个探究问题,其彼此独立,又有一定的联系. 它们不仅能深化学生对向量加法运算律的认识,还能促进学生数形结合思想、类比思想等的形成.
实践证明,高效的探究活动须全体学生积极主动地参与,那么教师应为学生提供充足的时间与良好的探究平台,鼓励学生通过小组合作的方式不断深化对知识的理解,并在积极的讨论与交流中进行总结、展示. 学生因亲历互动、交流、质疑与思辨的过程,不断积累探究经验与研究方法,故能够更加深刻地认识向量加法法则.
第四个环节:实际应用
题1 如图6所示,已知点O是正六边形的中心点,请在图中作出以下几个向量:①+;②+;③+.
题2 解决情境2中的问题.
评析 任何知识的学习都是为实际应用服务的,上述两个问题是检验以上教学成效的重要指标,尤其是题2要求学生解决情境2中的问题,起到了首尾呼应的效果. 学生在新知建构的基础上再回过头来重新思考原来的问题,能够产生不一样的学习体验.
上述两个问题都凸出了向量加法在复杂图形中的应用,着重考查学生对新知的加工处理能力以及思维能力. 学生的数学能力的强弱,体现在解题思路上. 因此,数学教学离不开解题训练,问题的设计与选择至关重要,过于简单的问题达不到产疑、启思的效果,而过于复杂的问题又让学生寸步难行.
在解题教学中,若教师自顾自地讲解,将浪费学生思考的时间. 因为教师的思维起点与学生的认知水平不在同一个层次,教师的思路无法替代学生的思路. 要使解题教学发挥其价值,最好的方法是在尊重学生的基础上,鼓励学生独立思考,教师“放权”给学生,让学生勇敢地表达、展示,只有会“倾听”的教师才是好教师. 学生展示思维的过程,是发展个性的过程,是树立创新意识和提高核心素养的过程.
教学思考
1. 尊重个体差异是“以学定教”的前提
哈佛大学的加德纳教授认为:每个人的智力都是多元的,每个人都拥有不同程度的九种智力,这些智力组合在一起就形成了个体差异. 对于学生而言,个体差异是客观存在且不可否认的事实,不同的学生存在不同的智力强项、心理倾向与学习风格. 教师应充分尊重学生客观存在的个体差异,尽可能地发展学生的智力强项,让每一个学生都能在教学中获得不同程度的发展,让课堂教学效益最大化.
面对不同认知水平的学生,教师应从学生思维能力的差异着手,由浅入深地设计出层次分明的问题,让问题成为学生思维成长的“脚手架”.
对于基础较薄弱的学生,教师应特别关注他们对基础知识的掌握,不论是课堂教学的哪个环节,都要做到不抛弃、不放弃,用平等的眼光去看待他们,用更多的耐心去培养他们,尽可能让他们在课堂中受到更多的关心,使其收获学习的成就感,建立学习信心;對于学优生,教师需要关注的是这类学生所提问题的深度与新颖程度,观察他们的解题技巧与创新意识的发展,必要时可适当地“加餐”,以拔高他们的思维.
对于基础较差的学生而言,虽然有情境探究作为基础,但在实际应用环节中仍然存在不能充分理解题意、害怕计算等问题. 此时,教师可有意识地放慢教学速度,认真倾听这部分学生的解题思路,必要时通过耐心引导与鼓励,让他们真正体验向量加法法则的内涵.
承认并尊重学生的个体差异,利用各种教学手段杨其所长,是实施“以学定教”的前提.
2. 教师精心预设是“以学定教”的关键
凡事预则立,不预则废. 新课标明确学生在课堂中的主体地位,但教师的引导作用不容小觑. 虽说如今的课堂强调学生主体参与,注重师生、生生的合作交流与动态生成,但这一切都是在教师精心预设的基础上有计划、有目标、有组织地实施. 缺乏精心预设的课堂,只能是一盘散沙,最终落得个假热闹.
想让课堂教学达成预期目标与成效,教师不仅要在课前充分了解学情,还要在课堂中掌握好学生的思维动向,适当时给予点拨与引导,让学生的思维围绕核心问题展开. 例如认知水平较弱的学生解决探究3的问题时,教师要关注他们的思维动向,必要时进行点拨,让他们结合图形与向量加法法则分析问题.
如图7所示,教师精心预设一般分为原行为阶段、新设计阶段与新行为阶段. 本节课笔者以五个逐层递进的问题有效激发学生思考,学生的行为表现也基本在笔者的预设范围内,由此产生的教学成效较明显.
3. 发展核心素养是“以学定教”的目标
如今的学科教学都以发展学生的学科核心素养为目标,数学教学亦不例外. 数学核心素养涵盖六大要素,一堂好课,必然是围绕学生的六大素养进行的. 要让核心素养在课堂中扎根,就要将培养学生核心素养的理念根植于每一个教育工作者的脑海中.
尽管随着时代的进步与发展,学生获取知识的途径越来越丰富,但课堂依然是进行教育教学的主阵地,是学生汲取知识、发展核心素养的重要场所. “以学定教”能有效启发学生的思维,在“以生为本”的基础上,提升每一个学生的思维品质,让每一个学生获得“三会”能力.
总之,发展学生的数学核心素养是时代赋予教师的任务,“以学定教”是实现这一目标的根本. 鉴于此,每一个教师都应树立“以生为本”“立德树人”的教育理念,不忘数学教学的初衷,做好精心预设,有效培养学生的创新意识,让数学学习真实发生.

