落花时节又逢君 多法齐出似腾云——谈2023 年高考新课标ⅠⅠ卷第21 题的深度探究

福建省福清第三中学 (350000) 唐洵

1 题目呈现

题目1(2023 年高考新课标ⅠⅠ卷第21 题) 已知双曲线C的中心为坐标原点,左焦点为,离心率为

(1) 求C的方程; 线C的中心为坐标原点,左焦点为,离心率为

(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于P,证明: 点P在定直线上.

2 解法探究

2.1 第(1)问解析

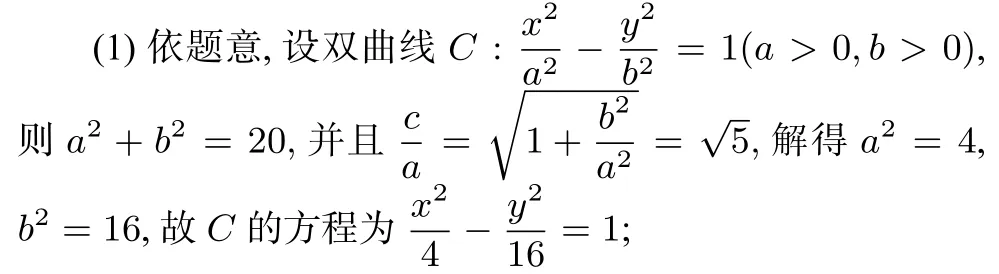
注由于第(1)问较为简单,仅给出参考答案如上;在求解第(2)问之前,先作图1 如上.

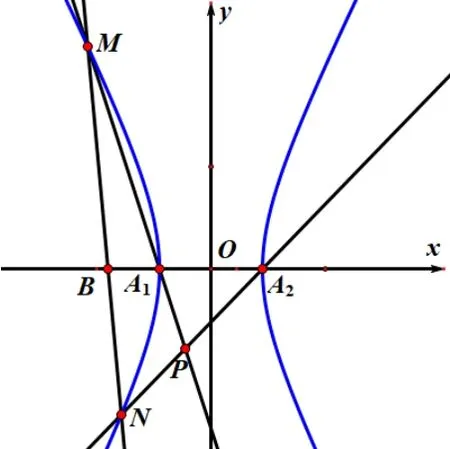
图1

2.2 第(2)问解析

综上所述,点P在直线x=-1 上.

解法3(设线联立2)设过点(-4,0)的直线为x=ty-4,将其与双曲线方程联立,整理得(4t2-1)y2-32ty+48=0,Δ＞0 且4t2-1／=0. 设M(x1,y1),N(x2,y2),P(x0,y0),则

3 拓展延伸

结论2～4 的证明与结论1 类似,这里不再赘述;对于焦点在y轴上的椭圆也双曲线,也有类似结论,有兴趣的读者可以自行归纳整理.

4 背景挖掘

事实上,题目1 与题目2 的命题背景都出自圆锥曲线中的极点与极线的相关结论.

(1)极点极线定义.

几何定义如图2, 点P不是圆锥曲线上的点(且非中心), 过点P引两条割线依次交圆锥曲线于E,F,G,H, 连接EH,FG交于N,连接EG,FH交于M,则直线MN为点P对应的极线;同理,直线PM为点N对应的极线,直线PN为点M对应的极线,ΔPMN称为自极三角形;特别地,若P在圆锥曲线上,则过点P的切线即为点P对应的极线.

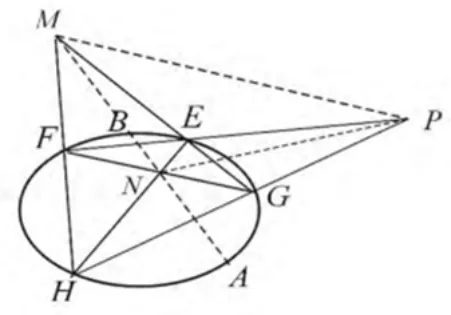
图2

5 类题赏析

题目3(2023 年淄博一模第21 题) 已知抛物线C:y2= 2px(p＞0) 上一点P(2,t) 到其焦点F的距离为3,A,B为抛物线C上异于原点的两点. 延长AF,BF分别交抛物线C与点M,N,直线AN,BM相交于点Q.

(1)若AF⊥BF, 求四边形ABMN面积的最小值; (答案:y2=4x,最小值为32)

(2)证明: 点Q在定直线上.

赏析作出第(2) 问图形如图3 所示, 易知点Q在点F(1,0)对应的极线x=-1 上.

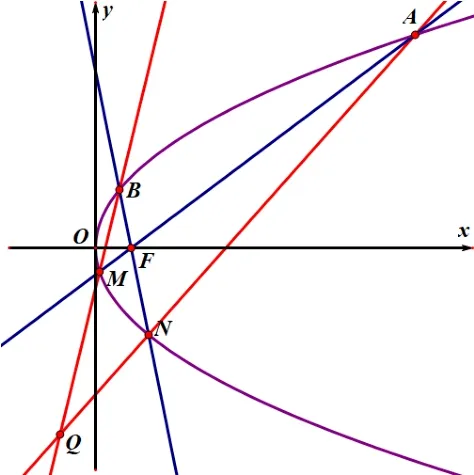
图3

(2)若过F的直线与双曲线C交于M,N两点,探究: 直线A1M,A2N的交点Q是否在某条定直线上? 若是,求出该定直线的方程;若不是,请说明理由.

赏析作出第(2) 问图形如图4 所示, 易知点Q在点F(2,0)对应的极线上.

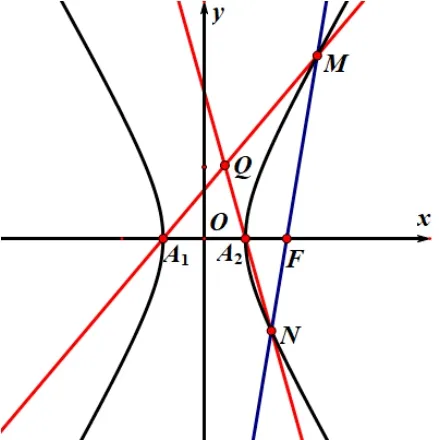
图4

题目5(福建省2023 届高中毕业班适应性练习题)已知圆A1:(x+1)2+y2=16,直线l1过点A2(1,0)且与圆A1交于点B,C,BC中点为D,过A2中点E且平行于A1D的直线交A1C于点P,记P的轨迹为Γ.

(2)坐标原点O关于A1,A2的对称点分别为B1,B2,点A1,A2关于直线y=x的对称点分别为C1,C2,过A1的直线l2与Γ 交于点M,N,直线B1M,B2N相交于点Q. 请从下列结论中,选择一个正确的结论并给予证明.

①ΔQB1C1的面积是定值; ②ΔQB1B2的面积是定值; ③ΔQC1C2的面积是定值.

赏析作出第(2) 问图形如图5 所示, 易知点Q在点A1(-1,0)对应的极线x= -4 上,故ΔQC1C2的面积是定值.

图5