2023 年高考新课标Ⅰ卷第17 题的解法分析

广东省惠州市教育科学研究院 (516001) 李晓波

2023 年的高考已落下帷幕,今年的新课标Ⅰ卷第17 题题目简明而清新,突出考查学生的三角函数知识与数形结合思想及数学思维的严谨性,要求学生能深刻理解三角形的本质,三角形中边与角的关系. 它看起来难度不大,但答题情况并不理想,笔者按自己的解答撰文评析,并对此题进行了拓展改编,供读者参考.

题目(2023 年高考新课标Ⅰ卷第17 题)在ΔABC 中,A+B =3C,2 sin(A-C)=sin B.

(1)求sin A;(2)设AB =5,求AB 边上的高.

一、试题分析

从试题自身来看,主要考察了正余弦定理、诱导公式、两角和与差的三角函数值,同角三角函数关系、三角形面积公式等. 本试题构建了一个锐角三角形模型,通过预设一些边角关系,求线段与角的值.

从思想方法来看, 主要考察化归思想与数形结合思想.从核心素养来看,主要考察逻辑推理、直观想象、数学运算素养,从关键能力来看,主要考察了逻辑推理能力、运算求解能力.

从命题思路来看,在第(1)问中,命题者通过构建三角形中的2 个角的关系,需要解题者利用三角形内角和这一隐形条件, 也是考查三角形的本质, 解出一个角C, 再构建一个2 sin(A-C) = sin B,即三个角的三角函数关系,考查学生化归的能力,通过公式和∠C 的值,最终把三个角关系,化为一个角的三角函数,即求解sin A 的值.为

第(2)问中,命题者通过构建一个面积是确定的三角形,来求一边上的高. 学生需要利用第(1)问的结论,即角的值,结合第(2)问条件AB的值,通过正弦定理或余弦定理,确定三角形的边,从而求出AB边上的高,当然也可以用等面积法来求高.

还可以看出,命题者为了降低难度,构建了一个锐角三角形,减少了学生分类的困难.

二、解法分析

首先,考虑第(1)问的4 种解法.

图1

图2

三、试题的改编

原题的模型是一个静态的问题,只涉及三角形的内部特征,笔者尝试在不改变原始条件的情况下,把静态问题变成动态问题,由三角形内部扩展到外部.

改编题已知在ΔABC中,A+B= 3C,2 sin(A-C) =sinB.

(1)求sinA;

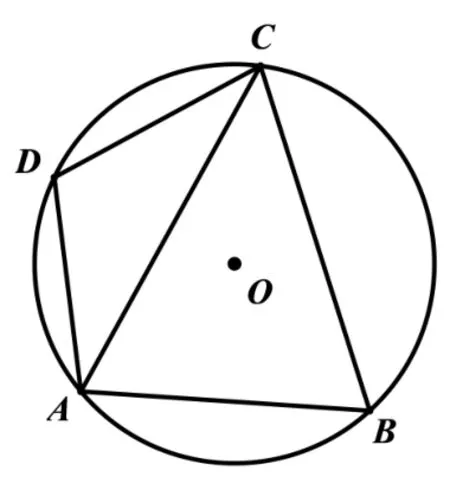
图3

(2)设AB=5,若D为三角形ABC的外接圆上的一点,且点D在劣弧AC上,求SΔACD

解法2(几何法)记ΔABC的外接圆圆心为O.

如图4,作OM⊥AC,则M为AC的中点, 延长OM至与交于E, 当D与E重合,SΔACD的面积最大, 2R=此时则

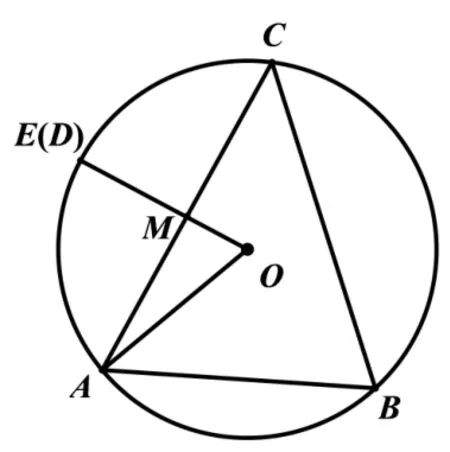
图4

评析此改编方式把一个静态的三角形变成了一个动态的三角形,由只分析三角形内部到三角形外部.