对一道不等式证明题的多角度探析

浙江省绍兴市柯桥区越崎中学 (312050) 孙昌洋

1. 引言

高中不等式的证明一般出现在高考压轴题中,往往跟导数结合较为紧密,因其灵活性高,技巧性强,很多学生不得不放弃. 然而,此类问题依然有法可依,有法可循. 我们必须弄清思路,找对方法,攻克思维障碍与恐惧心理,对不同层次的学生均能有所斩获. 本文以高三复习课中的一道不等式证明题为例,对不等式的证明问题进行了多角度的分析与概括[1],理清了问题解决的一般思路和方法,开拓了解题新思路与学术新视野[2],有效发散了数学学习中的学科思维,真正让核心素养得到落实与提升,让数学水平在无形中得到提高.

2. 不等式证明的多角度探析

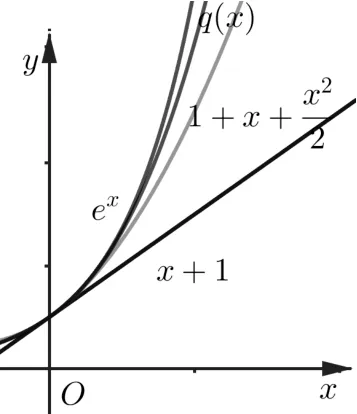
图1

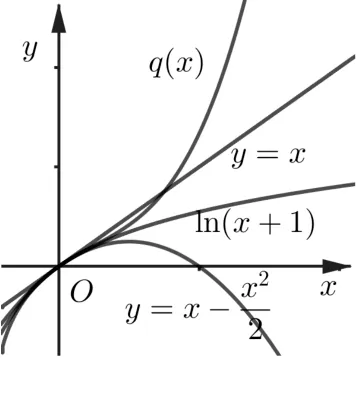
图2

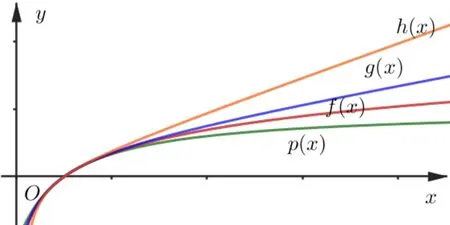
图3

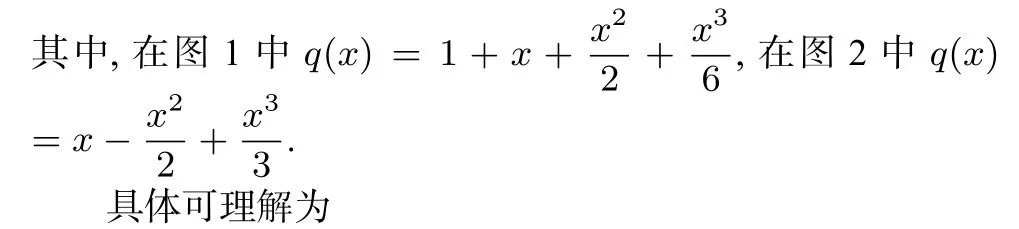
3 结束语

本文从传统作差分析、隔离分析再到适当放缩技巧拓展,三个角度共六种方法对一道不等式证明习题进行了全面分析,旨在通过发散思维,理清学生在解题中可能遇到的困境以及可行之解,在头脑中形成一张解题思维网,聚焦与凝结数学运算、逻辑推理、数学建模等核心素养,培养数形结合、分类讨论等解题技巧与数学思想. 一题多角度、多技法能让思维障碍得到点拨,解题捷径变得显然,易错困境得到规避.

在高中数学的解题中,我们会遇到很多可以多角度一题多解的题目,如各种函数最值的求法、数列的放缩、空间角的计算等等,我们可以多思考,多尝试,不是考试要求一题多解,而是一题多解能够发散我们的思维,聚焦我们的素养,让我们形成解题的必备品格与关键能力,而其本身蕴含着极大的数学思想方法,渗透在考试的各种题型中,让我们的发挥游刃有余,水到渠成.