一种连续梁桥高效阻尼体系

李子阳, 许 浩, 张 强, 杨巧荣, 徐子东

(上海大学力学与工程科学学院, 上海 200444)

连续梁桥具有刚度大、伸缩缝少、行车平稳等优点, 广泛应用于城市桥梁、山区高架桥和跨越江河湖海的桥梁[1-2]. 连续梁桥作为路网的重要组成部分, 一旦在地震中遭到严重损坏, 震区交通生命线将被切断, 进而导致更大的生命财产损失. 因此, 如何保护桥梁工程、采取何种措施把桥梁的振动对桥梁的危害控制在容许范围之内, 具有十分重要的意义. 目前, 桥梁减隔震技术的发展已经比较成熟, 尤其是以黏滞阻尼器、盆式橡胶支座等为代表的减隔震装置[3-5].

虽然黏滞阻尼器已经广泛应用于实际工程中并取得了较好的隔震效果[6], 但张恒晟等[7]通过试验发现在输入较小的位移时, 阻尼器的阻尼力会明显低于理论值, 不能充分发挥其耗能作用; 为解决这一问题, Constantinou 等[8]率先研究了肘节支撑阻尼器, 并对设置了该阻尼器的钢框架结构进行了振动台试验, 结果表明该阻尼器在发生很小的侧移时就输出较大的阻尼; 2007 年, 周云等[9]开发了巨型框架-耗能支撑结构新体系, 并对新体系进行了罕遇地震作用下的弹塑性时程分析, 指出当跨层布置的耗能支撑设计得当时, 可用较少的支撑数达到较好的减震效果. 2014 年, Raju 等[10]对附加肘节支撑和剪刀型支撑阻尼器的3 层钢结构1/4比例模型进行振动台试验, 结果表明2 种位移放大型阻尼器均能显著减小结构的响应; 2015年, 靳旭等[11]在双出杆型黏滞阻尼器中增设了一个副缸, 用于安装齿轮放大机构, 并以一栋12 层的钢筋混凝土框架作为原型结构, 对不安装阻尼器、安装普通阻尼器和安装位移放大2倍的阻尼器等3 种情况进行了多遇和罕遇水准下的时程分析, 验证了该阻尼器的减震控制效果; Londoo 等[12]通过有限元软件模拟了结构地震响应, 并对2 层结构进行了实时动态子结构试验, 指出随着放大倍率的不断增大, 阻尼器的位移、速度、阻尼力和耗能能力均得以放大;Smith 等[13]提出了消能伸臂的概念, 即利用核心筒的弯曲变形和外框架的剪切变形之间较大的竖向变形差, 放大黏滞阻尼器的输入位移; 2015 年, 刘文光等[14]设计了一种基于杠杆机构的位移放大型阻尼墙, 通过在黏滞阻尼墙和结构之间增设位移放大杠杆来放大阻尼墙的变形;2019 年, 郭彦等[15]研究了一种高效耗能新型阻尼器, 建立了力学分析模型并进行相关的力学试验, 结果表明理论模型可以有效评估新型阻尼器的力学性能; 2021 年, 颜学渊等[16]等设计了一种用于梁柱节点的位移放大型扭转阻尼器, 进行了性能试验并与有限元分析结果对比, 结果表明模拟曲线与试验曲线吻合较好, 并对有限元模型进行了参数分析, 研究各物理参数对阻尼器性能的影响.

上述方法均通过放大阻尼器的输入位移, 来达到提高阻尼器耗能效率的目的. 在此基础上, 本工作将盆式支座和位移放大型阻尼器相结合, 提出了一种连续梁桥高效阻尼体系(efficient damping system of continuous girder bridge, EDB). 为了研究这种体系在连续梁桥抗震中的适用性, 本工作对位移放大型黏滞阻尼器进行了力学性能试验, 并以一座6 跨连续梁桥为工程背景, 比较分析了不同减震结构的地震响应.

1 连续桥梁高效阻尼体系的提出

1.1 EDB 构造特点、工作机理

基于位移放大型黏滞阻尼器和盆式橡胶支座的力学性能及变形特点, 本工作提出的连续梁桥高效阻尼体系, 通过布置盆式橡胶支座来满足桥梁结构大的支承反力、大的水平位移和转角要求, 同时布置位移放大型黏滞阻尼器, 以提供运动阻力、耗减运动能量, 从而保护桥梁结构的安全. 在实际工程应用中, 可根据具体的力学性能要求, 对装置的杠杆放大倍率、摩擦系数以及黏滞阻尼器的参数进行相应调整, 以满足工程的需要.

EDB 主要由盆式支座和位移放大型阻尼器组成, 其中位移放大型阻尼器利用杠杆原理,在阻尼器与结构之间增设位移放大杠杆, 使得阻尼器在地震作用下的变形数倍于结构的变形,且放大了阻尼器两端的相对速度, 从而提高了阻尼器的耗能能力, 增大了结构的附加阻尼. 具体构造示意图如图1(a) 所示, 位移放大型阻尼器的连接板与桥墩侧面固定连接, 连接板开有长圆孔, 以满足系统工作时的运动协调要求, 支点固定架和阻尼器固定架分别与主梁底面固定连接, 放大杠杆分别与连接板、支点固定架、阻尼器活动端通过插销铰接.

图1 EDB 示意图Fig.1 Schematic diagram of EDB

EDB 通过在阻尼器与结构之间增设位移放大杠杆, 使阻尼器的变形数倍于结构变形. 连续梁桥高效阻尼减震体系在水平地震作用下单个桥墩的模型示意图如图1(b) 所示. 图中,m1和m2分别表示为主梁和桥墩的质量;μd为盆式支座的滑动摩擦系数;kd为普通黏滞阻尼器内部刚度, 一般可忽略不计;c为普通黏滞阻尼器的阻尼系数;L、ηL分别为位移放大机构下、上部分的长度,η为位移放大机构的放大倍率. 当水平地震来临时, 地面运动将地震作用由基础传递至桥墩顶部, 由于主梁的惯性作用, 主梁保持不动, 此时桥墩墩顶与主梁之间发生相对位移μ, 杠杆围绕支点转动, 墩梁相对位移μ经η倍位移放大杠杆放大后传递给普通黏滞阻尼器活动端的位移为ημ.

1.2 位移放大的基本概念

典型的速度相关性黏滞阻尼器, 其阻尼力F和耗能E可表示为[17]

式中: ˙u为阻尼器两端的相对速度;α为阻尼器的阻尼指数; sgn(·) 为符号函数;c为阻尼器的阻尼系数. 若阻尼器受到一个振幅为A、圆频率为ω的正弦激励, 则输入的位移u和速度v可分别表示为

假设通过杠杆将阻尼器的输入位移u放大η倍, 则阻尼器的位移与速度分别为ηu、ηv,此时阻尼器的出力F1为

根据杠杆放大力学原理, 位移放大型阻尼器装置的阻尼力F′为[18]

该位移放大型阻尼器的耗能E′可以表示为

由式(6) (7) 可知, 位移放大装置可以有效提高黏滞阻尼器的阻尼力和耗能效率.

对不附加位移放大装置的普通黏滞阻尼器, 将其阻尼系数放大n倍, 则其阻尼力F′′与耗能E′′分别为

当n=η1+α时, 有F′′=F′,E′′=E′, 即当附加位移放大装置后, 放大增益效果相当于将阻尼器的阻尼系数提高至原来的η1+α倍.

2 力学试验

2.1 试验介绍

在第1.2 小节中可以看到, 杠杆放大倍率为η倍的位移放大型阻尼器的阻尼力和耗能是普通黏滞阻尼器的η1+α倍. 为了验证EDB 的放大效果, 本工作设计了一组普通黏滞阻尼器和附加3 倍位移放大装置的黏滞阻尼器力学性能对比试验. 本试验所使用普通黏滞阻尼器(viscous damper, VD) 的系数c为32 kN/(m/s)0.42. 阻尼指数α为0.42. 阻尼器的力学性能参数如表1 所示.

表1 阻尼器的主要参数Table 1 Key parameters of damper

本试验采用100 kN 压缩试验机, 试验设备作动器最大振幅为±300 mm, 作动频率范围为0～50 Hz. 试验设备加载方向为水平加载, 为配合试验设备, 试验加载图如图2 所示. 图中杠杆动力臂长度为90 mm, 力臂长度为270 mm, 放大倍率为3 倍. 图3 为现场加载图.

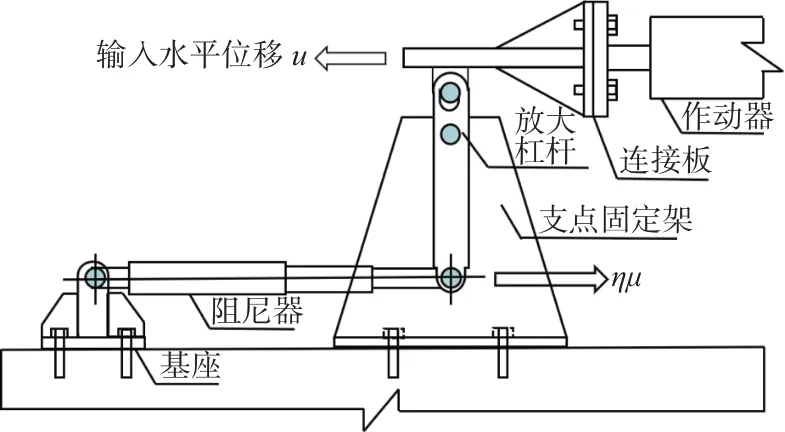
图2 试验加载图Fig.2 Loading diagram

图3 现场加载图Fig.3 Live loading diagram

2.2 加载工况

为了对比分析EDB 和VD 的力学性能, 本工作设计了在相同加载位移的基础上改变加载频率的工况, 试验采用位移控制的正弦加载, 加载频率分别为0.13、0.40 和0.80 Hz. 试验加载方案如表2 所示.

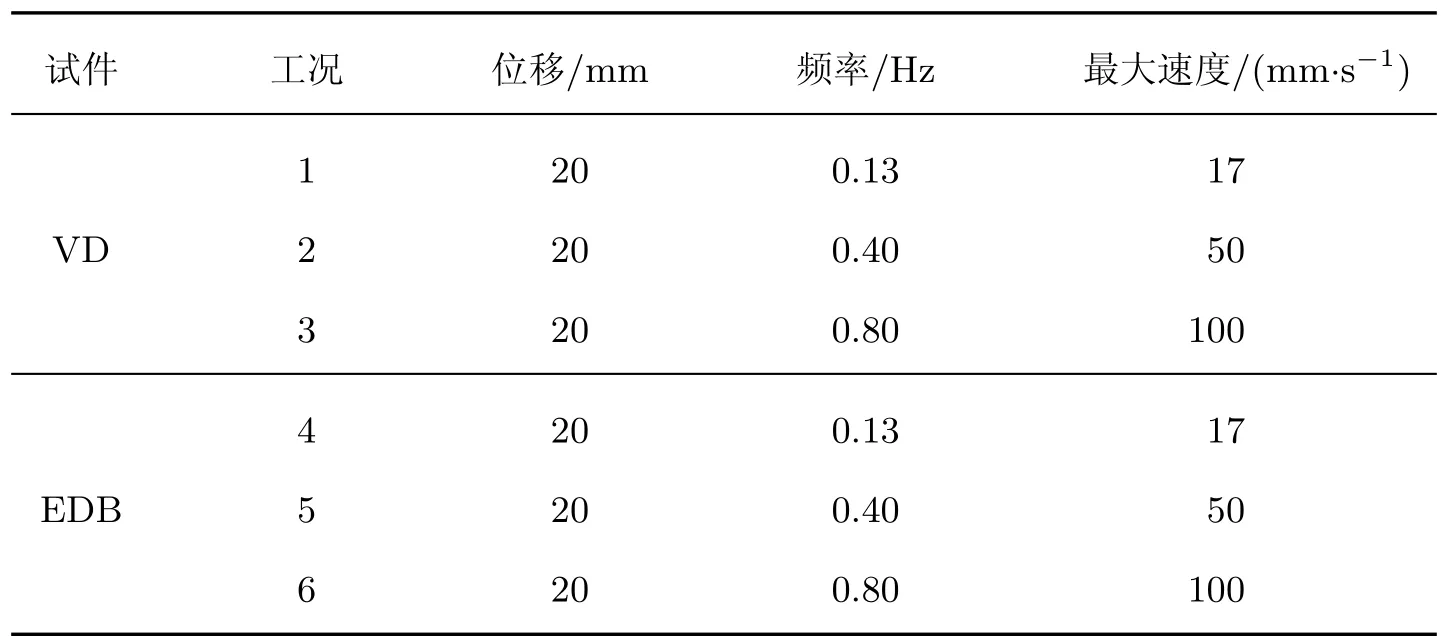
表2 试验加载方案Table 2 Test scheme of damper

2.3 试验结果

图4 为VD 和EDB 在不同加载频率下滞回曲线对比. 图中各工况下滞回曲线饱满, 滞回曲线符合典型黏滞性阻尼器本构特征, 阻尼器耗能良好. 通过对比EDB 和VD 的滞回曲线可以得到, 在相同加载位移与频率下, EDB 的耗能效率相对于VD 有明显提高. 在频率为0.13、0.40 和0.80 Hz 时, EDB 最大阻尼力分别为VD 的4.44、5.09 和5.48 倍, 平均放大5.01倍; 耗能分别为4.40、4.76 和5.30 倍, 平均放大4.82 倍.

图4 各工况滞回曲线对比Fig.4 Comparisons of hysteretic curves under different operating conditions

表3 给出了VD 和EDB 各工况下理论值与试验值的对比. 通过各工况试验值与理论值的对比可以得到, 试验结果与理论值基本吻合. VD 最大阻尼力与理论值平均误差为8.64%, 耗能平均误差为6.48%; EDB 最大阻尼力与理论值平均误差为2.40%, 耗能平均误差为3.60%.

表3 阻尼力及耗能的理论值与试验值对比Table 3 Comparisons of theoretical and experimental values of force and energy consumption

3 地震响应分析

3.1 工程实例有限元建模

高烈度区多跨混凝土连续梁桥跨径为40+4×65+40 m, 总长为340 m, 桥面全宽30 m(3 (非机动车道) + 24 (行车道) +3 (非机动车道)), 纵坡坡度2%. 技术标准: 设计荷载等级为公路级-Ⅰ级; 桥梁设计洪水频率为1/100; 设计基准期为100 年; 设计安全等级为一级; 抗震设防类别为B 类; 上部结构为六跨预应力混凝土变高度连续梁, 单箱单室截面, C50 混凝土,跨中梁高1.7 m, 支点处梁高3.6 m, 端支点梁高1.7 m, 梁高按2 次抛物线变化. 本桥下部结构采用柱式墩, 桥墩和承台采用C40 混凝土, 1～6# 墩设计为圆形截面独柱式桥墩, 7# 墩为双柱式桥墩, 1～7# 墩高分别为21.3、20.5、20.0、18.7、16.3、14.1 和13.2 m. 当墩高H ＜15 m时, 墩身直径为1.6 m; 墩高H ＞15 m 时, 墩身直径1.8 m. 桩基础采用钻孔灌注桩, 桩身直径1.5 m, 采用C40 混凝土.

本工作采用SAP2000 建立了3 维空间桥梁计算模型. 连续梁桥的主梁和桥墩均采用软件中的梁单元模拟, 单元质量采用集中质量表示; 承台按刚体模拟, 墩底与承台中心及桩顶中心节点作为主从节点连接; 采用弹簧单元间接模拟桩-土之间的相互作用; 采用快速非线性分析(fast nonlinear analysis, FNA) 方法对模型进行求解. 计算模型如图5 所示.

图5 多跨度连续梁桥3 维空间有限元模型Fig.5 Three dimensional finite element model of multi-span continuous girder bridge

3.2 减震方案

为研究连续梁桥高效阻尼体系对阻尼器耗能及结构响应的影响, 本工作将基于如下3 种方案进行地震响应分析比较.

方案1 原隔震模型. 主梁和桥墩之间使用盆式支座, 其中3# 墩设置固定支座, 其余各墩设置活动支座.

方案2 附加普通黏滞阻尼器结构(viscous damper-structure, VD-S). 在方案1 的基础上, 每个活动墩增设一个普通阻尼器.

方案3 附加连续梁桥高效阻尼体系结构(efficient damping system of continuous girder bridge-structure,EDB-S).在方案1 的基础上,在每个活动墩增设一个3 倍位移放大型阻尼器.

EDB 的水平力学性能包括盆式支座的摩擦力和位移放大型黏滞阻尼器的阻尼力, 二者是并联关系, 其中盆式支座采用程序中Rub-Isolator 连接类型进行模拟, 其力学性能可通过双线型理想弹簧单元进行表示; 位移放大型黏滞阻尼器用梁连接单元模拟支点固定架与杠杆, 用Damper 连接类型来模拟黏滞阻尼器, 将与桥梁结构连接端进行固接, 将支点固定架进行铰接处理. EDB 的布置方式如图6 所示. 由于本工作主要研究在纵桥向地震作用下连续梁桥的减震情况, 故阻尼器均沿纵桥向布置, 每个活动墩顶部设一个阻尼器, 共设6 个. 阻尼器主要参数如表4 所示.

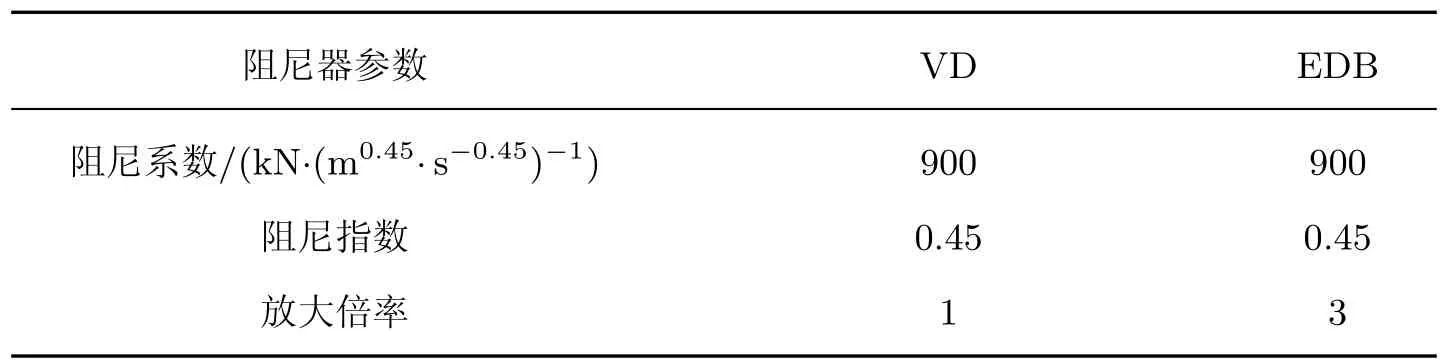
表4 阻尼器的主要参数Table 4 Key parameters of damper

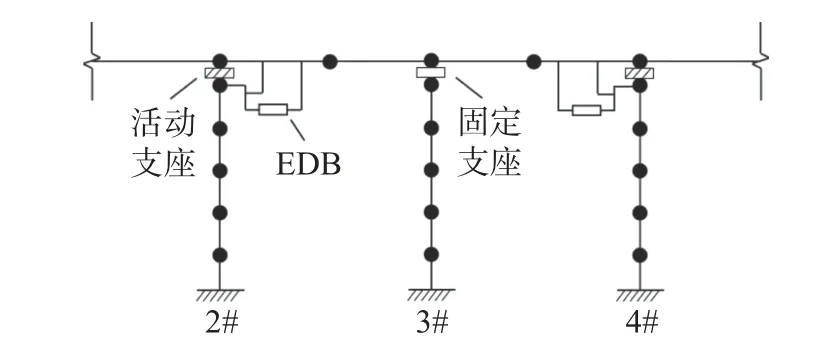
图6 EDB 布置图Fig.6 Layout diagram of EDB

3.3 地震动输入

本工作采用3 条人工波进行地震时程反应分析, 以《城市桥梁抗震设计规范(CJJ166-2011) 》中50 年超越概率2% 下的加速度反应谱作为目标谱进行生成, 阻尼比取为0.05. 图7显示了3 条人工波加速度反应谱.

图7 3 条人工波加速度反应谱Fig.7 Acceleration response spectrums for three simulated earthquake waves

3.4 原隔震模型地震响应分析

图8 为地震波1 作用下各墩减震前地震响应结果. 由图8(a) 可以看出, 在未设置阻尼器时, 所有桥墩墩底顺桥向弯矩之和为1.24×106kN·m, 剪力之和为8.02×104kN, 其中3# 墩共承担34% 的总剪力和40% 的总弯矩, 可见固定墩和活动墩所承受的弯矩和剪力很不均衡, 3#墩的墩底弯矩和剪力都明显高于其他墩上的内力, 这是因为3# 墩安装了固定盆式支座, 导致3# 墩的刚度较大. 因此当桥梁结构受到外部地震力时, 3# 墩会比其他桥墩承受更多的地震能量. 另外, 活动墩的墩梁相对位移则较大, 明显超过《公路桥梁盆式支座》中规定的盆式支座的极限位移(250 mm), 故需进行减震设计.

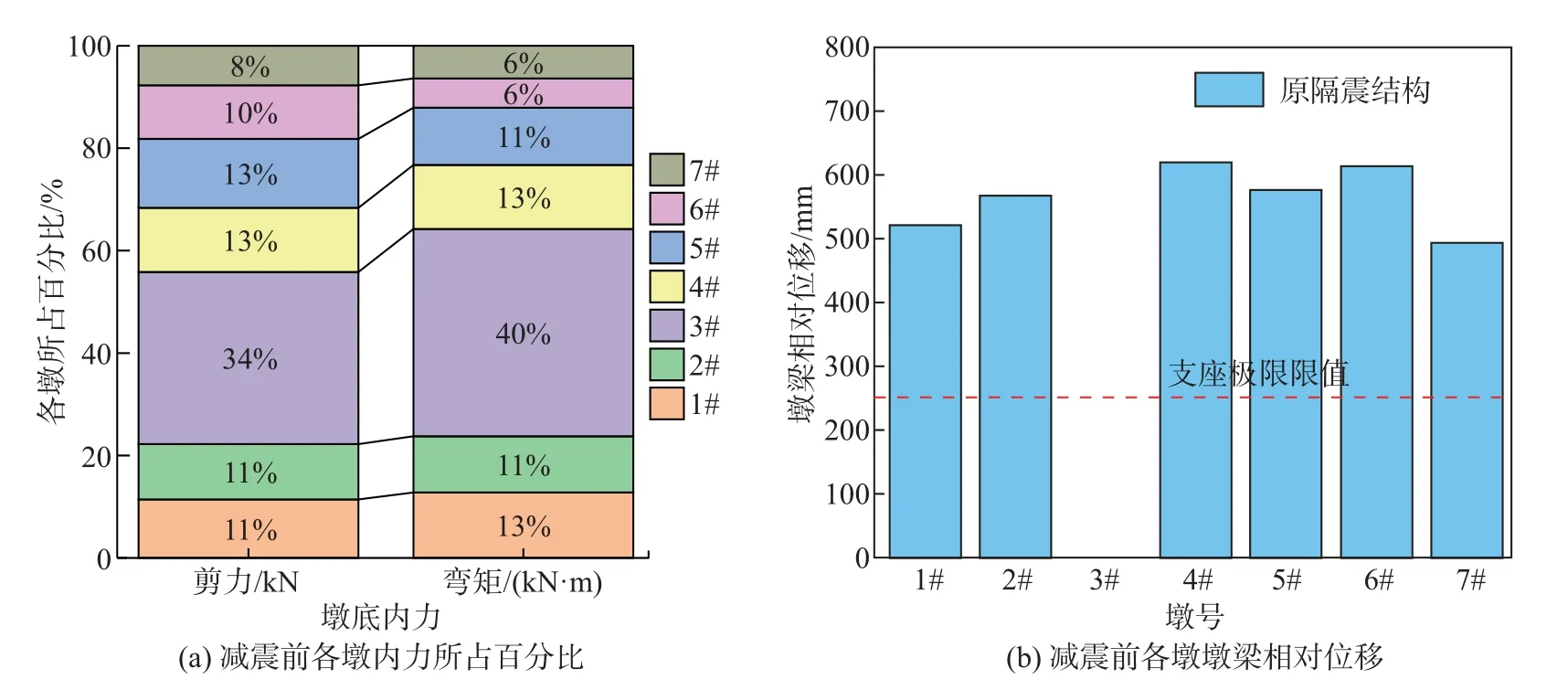
图8 地震波1 作用下各墩减震前地震响应结果Fig.8 Seismic response results of structures before damping design under Seismic wave 1

3.5 桥墩内力对比分析

图9 为3 种模型在设计地震动E2 下每个桥墩的墩底弯距和剪力响应对比, 图中时程分析的最终结果取各组计算结果的最大值. 从图中可知, 连续梁桥在设置阻尼器后固定墩的内力明显减小, 虽然部分活动墩的墩底内力有所增大, 但增幅不大. 通过对比3 个模型的内力结果可以看出, EDB-S 的减震效果明显优于VD-S. 相比于原隔震模型, VD-S 固定墩弯矩和剪力平均减小32.91% 和38.34%; EDB-S 固定墩弯矩和剪力平均减小52.87% 和63.20%.

图9 3 种模型的桥墩墩底弯矩和剪力响应对比Fig.9 Comparisons of bending moment and shear force at the bottom sections of three models

3.6 桥墩位移响应对比分析

图10 为3 种模型的位移响应对比. 从图10(a) 可以看出, 活动墩加上阻尼器后, 所有活动墩的墩梁相对位移均有不同程度的下降. 在原隔震模型中, 4# 墩墩顶的墩梁相对位移最大为612 mm. 相比于原隔震模型, VD-S 墩梁相对位移平均减小32.46%, EDB-S 平均减小49.81%,所有活动墩的墩梁相对位移均小于支座的极限位移(250 mm). 从图10(b) 中可知, 在减震前连续梁桥的主梁发生较大的位移, 最大位移达到685 mm, VD-S 最大主梁位移减小37.22%,EDB-S 最大主梁位移减小63.51%.

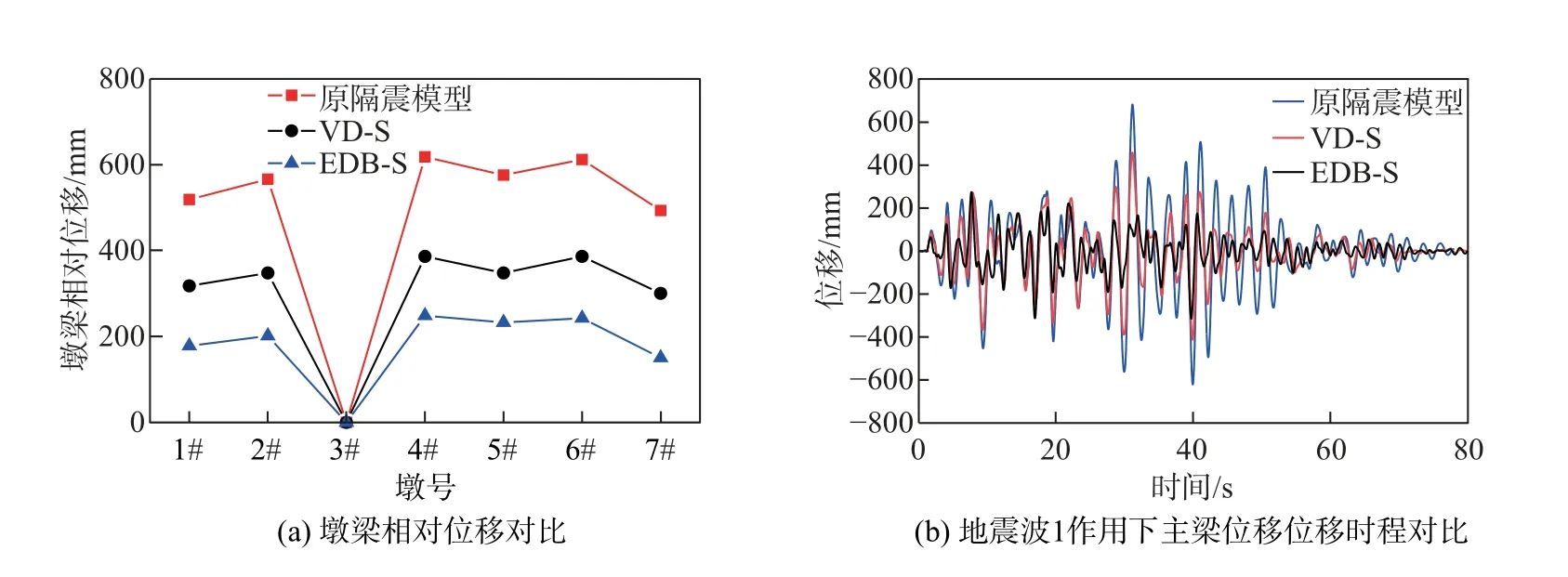
图10 3 种模型的位移响应对比Fig.10 Comparisons of displacement responses of three models

3.7 耗能分析

图11 显示了在地震波1 作用下VD-S 和EDB-S 黏滞阻尼器的滞回曲线. 从图11 中可以看出, VD-S 的阻尼器的最大位移是0.312 m, 而EDB-S 的阻尼器的最大位移是0.167 m, 位移减小了46.47%, 可见EDB-S 在桥梁体系中具有良好的位移控制能力. 将二者滞回曲线进行对比发现, EDB-S 的阻尼器在地震波1 作用下的最大阻尼力明显大于VD-S, 耗能能力也更强,是VD-S 的1.56 倍.

图11 地震波1 作用下VD-S 和EDB-S 滞回曲线Fig.11 Hysteretic curves of VD-S and EDB-S under Seismic wave 1

图12 为VD-S 和EDB-S 的能量曲线对比. 从图12 中可以看出, EDB-S 在输入位移小于VD-S 的情况下, 附加阻尼耗能依然比VD-S 强, 是VD-S 的1.50 倍; 同时振型阻尼能量下降了8.08%, EDB-S 和VD-S 的结构振型阻尼能量分别为191 800 和207 298 kN·m. 研究结果表明, 附加连续梁桥高效阻尼体系的桥梁结构可显著提高阻尼器耗能效率, 具有良好的位移控制能力, 能更有效地耗散地震输入能量, 减小结构动力响应.

图12 在地震波1 作用下VD-S 和EDB-S 的能量曲线对比Fig.12 Comparisons of energy dissipation curves between VD-S and EDB-S under Seismic wave 1

4 结 论

本工作提出了一种连续梁桥高效阻尼体系, 介绍了其构造特点和工作机理, 并设计了相关的力学性能试验; 以一座6 跨连续梁桥为工程背景, 比较分析了3 个减震方案在设计地震动E2 作用下的时程响应结果, 得到如下主要结论.

(1) 提出了一种连续梁桥高效阻尼器体系, 通过布置盆式橡胶支座来满足桥梁结构大的支承反力、大的水平位移和转角要求, 同时布置位移放大型黏滞阻尼器, 以提供运动阻力, 耗减运动能量, 从而保护桥梁结构.

(2) 位移放大型阻尼器通过附加放大机构来放大输入位移, 从而达到增加耗能的效果, 位移放大η倍的黏滞阻尼器的最大阻尼力和耗能与将阻尼系数放大η1+α倍的阻尼器具有接近的力学性能.

(3) 进行了一组普通黏滞阻尼器和附加3 倍位移放大装置的黏滞阻尼器力学性能对比试验, 并将试验值与理论值进行对比. 研究结果表明: 不同工况下位移放大型阻尼器的最大阻尼力和耗能相比于普通阻尼器均有明显提高, 2 种阻尼器的试验值与理论值基本吻合, 理论模型可有效评估位移放大型阻尼器的力学性能.

(4) 基于SAP2000 建立了一座实际6 跨连续梁桥的有限元模型, 比较分析了3 个减震方案在设计地震动E2 作用下的时程响应结果. 研究结果表明: 连续梁桥高效阻尼减震体系有效地耗散了地震能量, 减小了桥梁结构的地震响应.