基于3 种断裂韧性测试方法的试验分析

王永东, 包 陈, 宁 冬, 王谊清, 景 益, 浦承皓

(1. 上海核工程研究设计院有限公司, 上海 200233; 2. 西南交通大学, 四川 成都 610031;3. 生态环境部核与辐射安全中心, 北京 100082)

J积分常用来表征延性材料的弹塑性断裂行为, 在结构完整性评定中起到至关重要的作用. 目前, 断裂韧性评定多采用多试样法、卸载柔度法等. 多试样法于20 世纪70 年代初由Begley 等[1]提出, 该方法常用于确定J阻力曲线, 但其试验点分散性大, 无效点多, 且只能获得50% 置信度下的J阻力曲线[2]. 卸载柔度法是一种单试样法, 但对于非线弹性材料, 卸载柔度法不易应用, 在加卸载循环过程中会出现循环滞后现象, 并且裂纹断裂性能可能受到多次卸载行为的影响[2]. 20 世纪70 年代, Ernst 等[3]基于主导曲线函数[4]提出了载荷分离理论,并由此相继发展了规则化法[5-6]和Spb分离参数法[7-9]. 近年来, 国内学者[10-11]对载荷分离理论作了重要发展, 提出了改进的载荷分离Spb法. 本工作分别基于卸载柔度法、规则化法和Spb分离参数法开展某材料台阶型紧凑拉伸(compact tension, CT) 试样的准静态断裂韧性测试, 分析比较不同方法获得的J阻力曲线测试结果差异, 评估各试验方法对断裂韧性测试值的影响.

1 理论背景

1.1 卸载柔度法[12]

按照ASTM E1820—2018 对预制疲劳裂纹后的试样进行多个卸载再加载循环后, 得到如图1 所示的载荷-位移曲线, 图中COD 表示裂纹张开位移(crack opening displacement). 当试样处于弹性变形时, 载荷-位移曲线符合线性规律. 对弹性卸载循环内的数据{Pi,Vi}进行线性回归可得到测试柔度C,

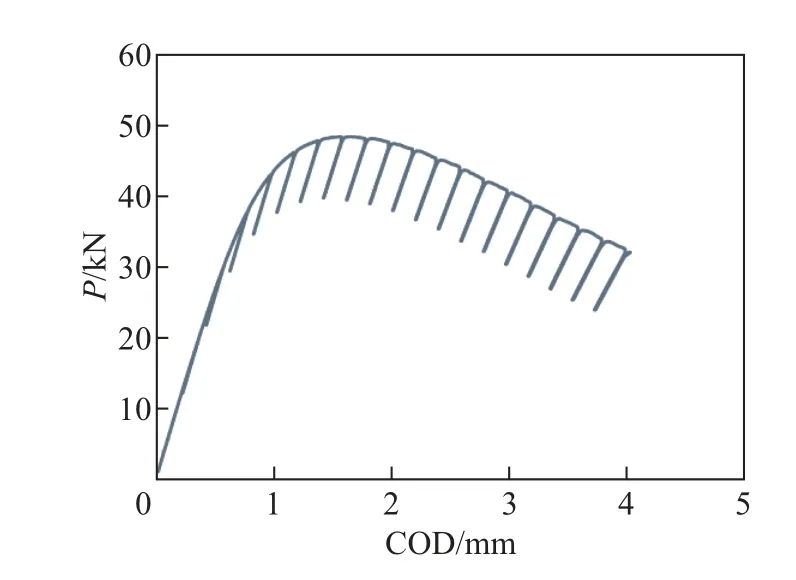
图1 卸载柔度法得到的载荷-位移曲线Fig.1 Load displacement curve obtained by unloading compliance method

式中:P为试样载荷;V为裂纹张开位移. CT 试样的实时裂纹长度由下式计算,

式中:a为试样裂纹长度;W为试样宽度;B为试样厚度;E为材料弹性模量;ci为多项式系数.

1.2 载荷分离法

1.2.1 载荷分离原理

试样的载荷P通常与几何尺寸、材料性能相关,

式中:σY为材料流动应力, 是材料屈服强度和抗拉强度的平均值;n为幂律材料的硬化指数;μ为泊松比.

量纲分析表明, 载荷P可表示为几何函数g(a/W) 与塑性变形函数h(Vp/W) 的乘积, 且两个函数是相互独立的,

式中:σ0为参考屈服应力;Vp为塑性位移.

定义分离参数Sij, 用于判断载荷分离假设是否成立,

若在塑性变形范围内, 试样的分离参数Sij保持恒定, 则表明该类试样符合载荷分离假设.分离参数Sij与韧带bi/W之间表现出良好的幂律特征,

不同参考韧带bj/W对应的幂指数m恒为常数, 并且系数k接近1. 函数g(a/W) 可表示为

从而有

进一步研究表明, 幂指数m与塑性因子η非常接近, 则载荷分离理论可描述为

1.2.2 规则化法[5-6]

由于难以直接确定塑性变形函数h(Vp/W) 的函数形式, Landes 等[6]定义了规则化无量纲载荷,

式中:ab为钝化修正裂纹尺寸,

f(σ)为钝化线斜率,不同标准下的推荐值不同,如ASTM E1820—2018 规范推荐f(σ)=2σY,而GB/T 21143—2014 规范推荐f(σ)=3.75σb.

如图2 所示, 从裂纹终止点对应的规则化数据点作一切线到余下的规则化数据点. 介于Vp/W=0.001 至切点之间的数据点以及终止点可表示为

图2 规则化法处理示意图Fig.2 Schematic diagram of normalization method

从待确定系数d1～d4后, 计算实时裂纹长度,

1.2.3Spb分离参数法[7-9]

Landes 等[6]根据载荷分离原理定义了对应锐裂纹试样的载荷分离参数,

式中: 下标p 对应锐裂纹试样; 下标b 对应钝裂纹试样. 根据裂纹几何函数表达式, 有

如图3 所示, 当锐裂纹试样的裂纹没有扩展时,Spb保持恒定; 当裂纹开始扩展时,Spb也随着裂纹扩展变化. 可将初始裂纹长度和结束时的裂纹长度作为标定点求解参数m, 从而得到实时裂纹长度. 相对于规则化法,Spb分离参数法与变形函数无关.

图3 Spb 分离参数法示意图Fig.3 Schematic diagram of Spb separation parameter method

2 试验条件

2.1 材料与试样

试验材料为某金属材料, 弹性模量214 GPa, 屈服强度615 MPa, 抗拉强度709 MPa. 参照ASTM E1820—2018 试验标准, 采用图4 所示的台阶型锐裂纹CT 试样开展准静态断裂韧性试验.

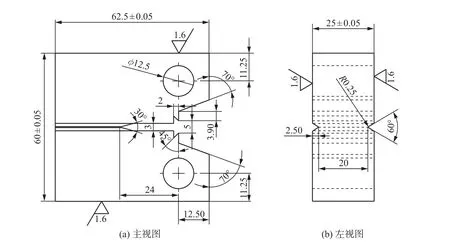
图4 台阶型锐裂纹CT 试样Fig.4 CT specimen with step type sharp crack

2.2 试验设备

断裂韧性试验在MTS 809 250 kN/2 000 N·m 电液伺服材料试验系统上完成, 控制系统为TestStarⅡ, 载荷和位移传感器精度均为0.5%. 采用MTS632.03F-30 型COD 引伸计测量CT 试样的加载线位移, 标距为5 mm, 量程为-3～12 mm, 精度为0.5%. 试验机自动记录试验过程中的载荷、位移、COD 等信息.

2.3 试验过程

首先, 参照ASTM E1820—2018 相关规定对试样预制疲劳裂纹. 试验预制裂纹长度增量约2 mm. 预制疲劳裂纹采用等ΔK控制, 既可保证裂纹扩展驱动力均匀, 还可确保裂纹尖端不出现大范围屈服.

完成疲劳裂纹预制后, 采用以下步骤测试J阻力曲线.

(1) 依据图2 所示卸载柔度法对预制好的试样进行循环加卸载, 当试样载荷达到最大值且下降约10%～15% 时停止加载. 单调加载阶段以位移控制, 速率为0.02 mm/s; 保持阶段以位移控制, 保持时间为2 s; 循环加卸载阶段以载荷控制, 速率为2 kN/s.

(2) 将试样置于电炉上加热, 当试样明显变蓝色时停止加热. 再次将试样安装到试验机上后拉开.

(3) 采用光学测量手段测出试样断面上预制疲劳后的裂纹长度和拉伸加载停机时的终止裂纹长度.

(4) 参照ASTM E1820—2018 标准推荐的卸载柔度法、规则化法以及Spb分离参数法这3 种方法对试验数据进行分析处理, 得到J阻力曲线.

(5) 对于Spb分离参数法, 另需将钝裂纹CT 试样以0.02 mm/s 的位移恒速率进行单调加载, 且最大加载位移需超过锐裂纹CT 试样的最大加载位移.

3 试验结果

3.1 基于卸载柔度法的J 阻力曲线

表1 给出了根据卸载柔度法得到的锐裂纹CT 试样的初始裂纹长度和终止裂纹长度. 图5给出了根据卸载柔度法得到的锐裂纹CT 试样的J阻力曲线.

表1 裂纹长度测量结果对比Table 1 Comparison of crack length measurement resultsmm

图5 基于卸载柔度法的锐裂纹CT 试样的J阻力曲线Fig.5 J-resistance curve of CT specimen with sharp crack based on unloading compliance method

3.2 基于规则化法的J 阻力曲线

图6 给出了根据规则化法得到的锐裂纹CT 试样的J阻力曲线.

图6 基于规则化法的锐裂纹CT 试样的J 阻力曲线Fig.6 J-resistance curve of CT specimen with sharp crack based on normalization method

3.3 基于Spb 分离参数法的J 阻力曲线

图7 给出了根据Spb分离参数法得到的锐裂纹CT 试样的J阻力曲线.

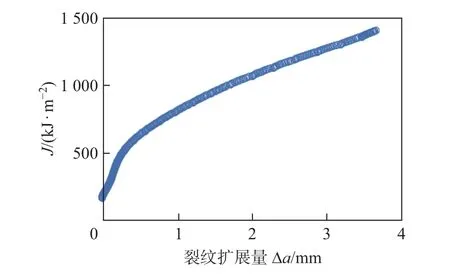
图7 基于Spb 分离参数法的锐裂纹CT 试样的J 阻力曲线Fig.7 J-resistance curve of CT specimen with sharp crack based on Spb separation parameter method

图8 给出了根据卸载柔度法、规则化法、Spb分离参数法这3 种方法得到的锐裂纹CT试样的J阻力曲线对比结果. 从图中可以看到, 3 种方法得到的J阻力曲线仅在裂纹扩展初期存在一定差异, 在裂纹扩展量达到一定程度后3 条曲线几乎重合, 其中基于卸载柔度法得到的J阻力曲线在初始阶段甚至出现了负的裂纹扩展量, 这是由于初始阶段裂纹扩展非常小, 柔度测量不够准确导致的. 此外, 由1.2.2 节可知, 规则化法采用了钝化修正, 而图3 显示Spb分离参数法在载荷-位移曲线开始分离后才能计算实时裂纹长度. 因此, 在裂纹扩展初期, 由规则化法得到的J阻力曲线与Spb分离参数法结果也存在一定差异.

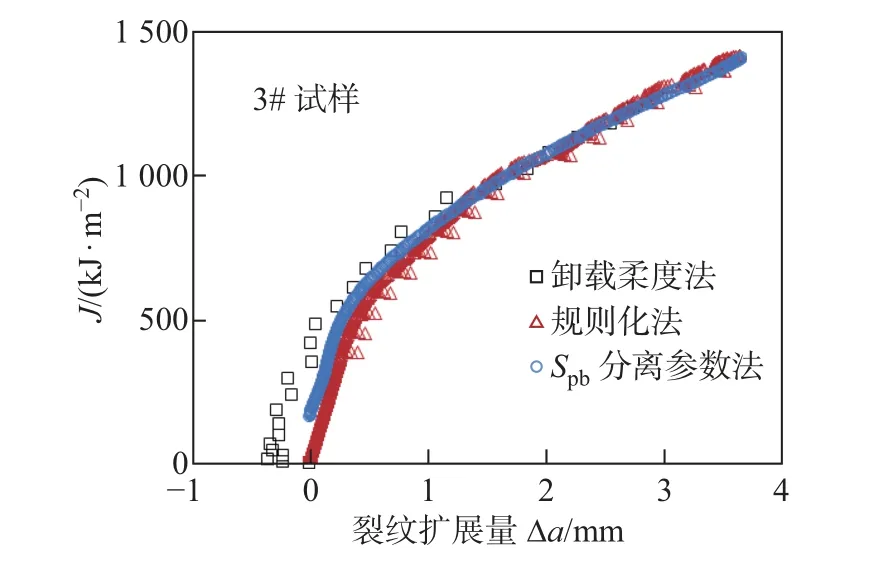
图8 基于不同数据处理方法的锐裂纹CT 试样J 阻力曲线对比Fig.8 Comparison of J-resistance curves of sharp crack CT specimens based on different data processing methods

4 J 阻力曲线的有效性判定

如图9 所示, ASTM E1820—2018 规定的有效数据区是由左、右界限线、上界限线和Δalimit竖直轴围成的封闭区域. 左界限线为0.15 mm 钝化线偏置线, 右界限线为1.5 mm 钝化线偏置线, 上界限线为过极限值Jlimit处横轴的平行线. 在有效数据区内至少有5 个数据点,在0.15 mm 和0.5 mm 钝化线偏置线之间至少有一个数据点, 在0.5 mm 和1.5 mm 钝化线偏置线之间至少有一个数据点.Jlimit的取值为(W -a0)σY/7.5.

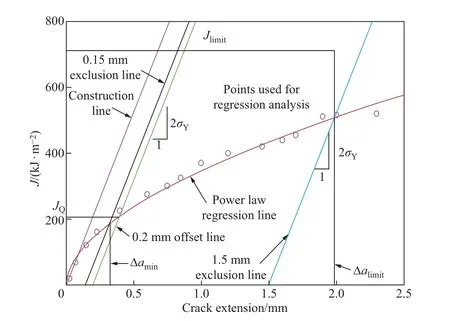
图9 阻力曲线有效数据判定[12]Fig.9 Definition of construction lines for date qualification[12]

对于封闭区域内的有效数据点, ASTM E1820—2018 推荐采用幂函数方程J=C1ΔaC2进行拟合, 拟合曲线与0.2 mm 钝化线偏置线的交点即为(JQ, ΔaQ). 当满足以下有效性条件时, 即B ＞10JQ/σY; (W -a0)≥10JQ/σY,JQ即可作为非尺寸敏感的特征启裂韧度JIC.

对图8 所示的3 种不同分析方法得到的J阻力曲线参照上述规定进行有效性判定, 结果如图10～12 所示.

图10 锐裂纹CT 试样J 阻力曲线有效数据区间分布(卸载柔度法)Fig.10 Interval distribution of effective data of J-resistance curve of CT specimen with sharp crack (unloading compliance method)

图11 锐裂纹CT 试样J 阻力曲线有效数据区间分布(规则化法)Fig.11 Interval distribution of effective data of J-resistance curve of CT specimen with sharp crack (normalization method)

图12 锐裂纹CT 试样J 阻力曲线有效数据区间分布(Spb 分离参数法)Fig.12 Interval distribution of effective data of J-resistance curve of CT specimen with sharp crack (Spb separation parameter method)

表2～4 分别给出了基于卸载柔度法、规则化法和Spb分离参数法的JIC有效性判定结果.可以看到, 3 种不同分析方法得到的条件启裂韧度JQ值均满足有效性判定条件, 其中基于卸载柔度法得到的临界启裂韧度JIC明显高于规则化法和Spb分离参数法, 基于规则化法得到的临界启裂韧度JIC值最低. 从工程应用的角度推荐采用规则化法测试材料的临界启裂韧度JIC, 因为该方法得到的结果偏于保守, 有利于工程结构的安全服役.

表2 有效性判定结果(卸载柔度法)Table 2 Effectiveness determination results (unloading compliance method)

表3 有效性判定结果(规则化法)Table 3 Effectiveness determination results (normalization method)

表4 有效性判定结果(Spb 分离参数法)Table 4 Effectiveness determination results (Spb separation parameter method)

5 结束语

由卸载柔度法得到的J阻力曲线与基于载荷分离原理的规则化法和Spb分离参数法得到的J阻力曲线差异较大, 而规则化法和Spb分离参数法得到的J阻力曲线非常接近. 造成差异的原因主要在于裂纹扩展初期3 种方法所采用的处理方式存在差异.

3 种方法均可以获得有效的JIC值, 其中卸载柔度法得到的JIC值略大, 规则化法和Spb分离参数法得到的JIC值较为接近. 基于规则化法可以得到偏保守的临界启裂韧度JIC, 有利于工程结构的安全服役.