高放废物处置库温度场解析

何路强, 周祥运, 孙德安

(上海大学力学与工程科学学院, 上海 200444)

在利用核能发电过程中会产生大量高放射性核废物, 高放射性核废物包含放射性强、毒性大、半衰期长且发热量大的核素, 会对人类与自然环境造成较大危害. 因此, 高放射性核废物的安全处置成为了一个亟待解决的问题. 经过几十年的研究探索, 目前各国学者普遍认为深地质处置是存储高放射性核废物最安全和可靠的方法. 高放射性核废物深地质处置的概念如下:把装有高放射性核废物的废物罐埋藏于距离地表500～1 000 m 深度的稳定地质岩体中, 利用工程屏障(废物罐和缓冲层) 和天然屏障(围岩地质体) 多重屏障系统来阻滞核素的泄露与迁移. 在KBS-3V 型处置库概念设计中, 沿处置隧道方向每隔一定间距开挖竖向的处置坑, 废物罐被安放于处置坑内, 废物罐与围岩之间的孔隙放置膨润土块体. 但在实际施工过程中, 由于机械开挖的缘故, 膨润土块与围岩之间不可避免存在施工接缝, 故计划用膨润土颗粒混合料来填充. 我国已经确定在甘肃北山建造深地质处置库, 首选内蒙古兴和县高庙子膨润土为缓冲/回填材料的基质材料, 并于2021 年6 月17 日开始进行北山地下实验室的建设.

高放射性核废物在其长期的衰变过程中会产生大量的衰变热, 导致处置库内缓冲材料以及围岩温度的升高, 而温度的升高会影响处置库的存储功能. 首先, 温度的升高使缓冲材料和围岩发生热膨胀, 热膨胀产生的热应力导致缓冲材料以及周围岩体出现热损伤[1]; 其次, 当地下水中存在钾离子时, 温度的升高还会导致膨润土的主要矿物成分蒙脱石发生伊利石化, 使膨润土的渗透性和膨胀性发生改变, 进而削弱膨润土对核素泄露和迁移的限制作用[2]; 最后, 温度的升高还导致核废物罐表面出现盐分聚积, 加速核废物罐的锈蚀. 在实际的处置库环境中,缓冲材料长期受复杂的热-水-力耦合作用, H¨okmark 等[3]、Xue 等[4]和Zhou 等[5]的研究成果表明缓冲层峰值温度大约出现在处置后的第10～20 年. 在处置的前20 年内, 围岩蠕变还在缓慢进行, 围岩地下水还未入渗到缓冲层中, 此时应力场和渗流场对温度场的影响是很小的, 温度场在多场耦合效应中起主导作用. 因此, 有必要对处置库内的单温度场分布特性进行研究.

目前, 许多学者借助数值模拟的方法对处置库温度场的变化规律进行了研究.Choi 等[6]利用ABAQUS 软件建立了处置库的热分析模型, 分析了处置库的温度场演化特征, 并通过该模型得到竖直处置的最佳隧道间距和废物罐间距, 分别为40、8 m, 而水平处置的最佳隧道间距和废物罐间距分别为25、2 m; 赵宏刚等[7]利用ANSYS 软件建立了处置库3 维热分析模型,得出单个废物罐近场岩石温度的发展规律, 发现影响废物罐表面峰值温度的最敏感因素是初始处置剩余衰变热; 徐少波[8]利用ANSYS 软件对处置库近场围岩温度进行了模拟, 发现废物罐的温度在第10 年达到最高, 且废物罐间距越小, 废物罐罐面温度受其他废物罐的影响就越明显; Finsterle 等[9]利用TOUGH2 软件建立了水平处置的单处置孔径向热分析模型, 分析了不同废物罐间距下的温度演化规律, 发现随着废物罐间距的增大, 中部废物罐表面峰值温度逐渐降低; Justinavicius 等[10]基于立陶宛处置库的概念设计, 利用ANSYS 和COMPASS 2 个软件分别建立了处置库的3 维热分析模型, 研究发现2 个模型得到的温度分布非常相似, 同时膨润土的导热系数对废物罐表面温度影响较大.

数值方法虽能较好地模拟处置库的温度分布情况, 但在进行一些几何参数分析(如废物罐半径、缓冲层厚度、隧道间距和废物罐间距) 时, 数值模型需要重新划分网格, 所涉及的计算量是巨大的, 而解析方法只需通过更改参数即可快速得出结果, 不失为一种好的选择. 基于Carslaw 等[11]提出的作用于无穷大岩体的点热源模型, Claesson 等[12]建立了线热源模型, 利用杜哈梅定理叠加瞬时热源解得到含时间项的热源解, 并将该热源解应用于KBS-3 型处置库温度分析; H¨okmark 等[3]在Claesson 等[12]的线热源模型基础上考虑了废物罐顶部、中部和底部的热流量差异, 建立了复合线源热模型, 利用该模型得到了对应的解析解, 发现高放射性核废物的初始衰变热功率对温度影响较为明显; Xue 等[4]建立了处置库的轴对称一维热传导解析模型, 并通过分离变量法求得了该模型的温度解析解, 研究了处置库的温度演化规律, 并进行了参数敏感性分析, 发现缓冲层的参数(导热系数和厚度) 对温度的影响较为显著; Zhou等[5]建立了处置库的轴对称2 维3 层传热模型, 采用拉普拉斯变换法和傅里叶变换法求出了对应的温度场半解析解, 通过Crump 反演得出处置库的时间域温度演化规律, 并在此基础上与已有的线热源解进行对比, 验证了模型的有效性, 同时对隧道间距和废物罐间距等因素对废物罐表面温度的影响进行了分析.

本工作基于KBS-3V 型处置库概念设计, 建立了处置库轴对称2 维传热解析模型, 利用有限傅里叶变换法、分离变量法和冲量定理法得到了处置库非稳态温度场解析解, 并采用在岩壁温度上叠加缓冲层温度差的方法得到了废物罐表面温度, 在此基础上分析了材料热参数、核废物衰变参数以及几何参数对废物罐表面温度的影响, 为后续处置库的安全性能评估和热量尺寸设计提供参考.

1 单废物罐热传导模型

1.1 计算简图及控制方程

KBS-3 处置库概念设计模型包括竖直(KBS-3V) 和水平(KBS-3H) 2 种处置方式, 模型主要由竖井、斜井、处置隧道和沉积隧洞构成(见图1). 在KBS-3V 型处置方案中, 沿处置隧道以一定的废物罐间距开挖竖向的沉积隧洞, 装有高放射性核废物的废物罐被安置于沉积隧洞中, 废物罐与围岩之间的空隙用缓冲材料填充.

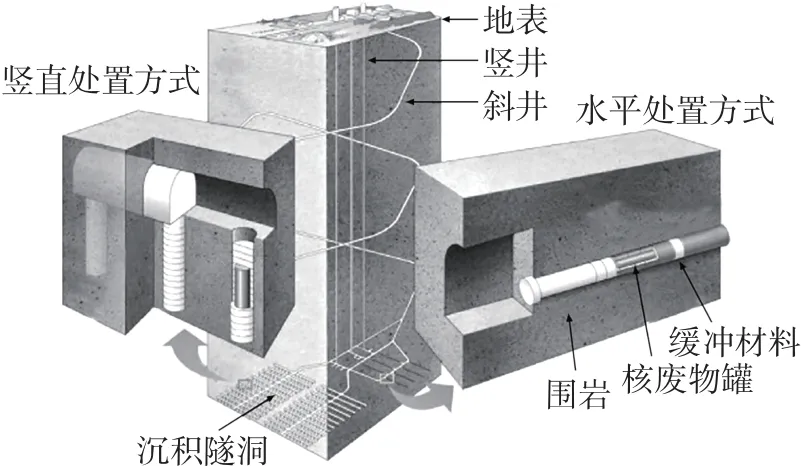
图1 KBS-3 处置库概念设计模型图Fig.1 Design model of KBS-3 repository

H¨okmark 等[13]研究发现, 缓冲材料的热特性对外层包裹围岩的温度值几乎没有影响, 且Zhou 等[5]用3 层传热模型得到的半解析解对该结论进行了验证. 基于以上结论, 本工作建立了处置库单层传热模型, 以研究处置库内围岩的温度演化规律, 计算模型如图2 所示. 图中,假设废物罐的半径为a, 高度为H, 围岩区域的半径由a向外无限延伸.

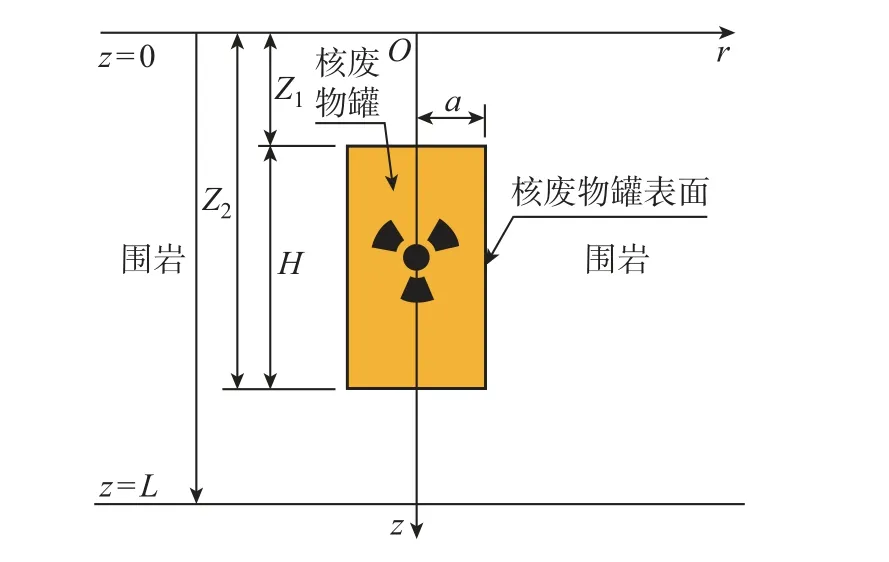
图2 单个核废物罐热分析计算模型Fig.2 Thermal analysis and calculation model of single nuclear waste canister

为得到单废物罐放热的温度场解析解, 对计算模型作如下假定: ①包裹废物罐的围岩均匀、各向同性且其热参数为定值; ②废物罐的热演化过程主要为热传导, 忽略热辐射和热对流引起的热传递; ③在控制方程的建立过程中, 由于罐材的导热系数远大于缓冲材料和围岩, 且罐材厚度比较薄, 因此这里忽略废物罐罐材厚度的影响. 采用柱坐标形式, 围岩的热传导方程可以表示为

式中: 下标R 表示围岩;TR(r,z,t) 为围岩温度(°C);χR=λR/(ρRcR);χR、λR、ρR、cR分别为围岩的热扩散系数(m2/s)、热传导系数(W/(m·K))、密度(kg/m3)、比热容(J/(kg·K));r为半径(m);z为深度(m);t为时间(s).

1.2 初始及边界条件的确定

地下温度会随着深度的增大而按一定的地温梯度增大, 因此计算中选取围岩的初始条件为

式中:t0为地表温度(°C);m为围岩沿深度方向的温度梯度(°C/m);z为任意一点的深度(m).

核废物衰变产生的衰变热通过废物罐的表面均匀发散. 由于废物罐上下表面的面积远小于侧面积, 故主要考虑侧面深度范围(z1到z2) 的散热情况, 废物罐侧面积为2πah, 因此围岩与废物罐交界面的边界条件为

其中,

式中:a为核废料罐的半径(m);H=z2-z1为核废物罐的高度(m);z1和z2分别为废物罐上、下表面的深度(m);P(0) 为废物罐刚入库时核废物的热功率(W);ti为冷却时间常数(s);ai为时间ti对应的指数系数;t(s) 为时间;P(t) 为时间t对应的剩余衰变热功率(W)[14];u(·)为阶跃函数.

无穷远处围岩的温度与相同深度的库外围岩温度相同, 即无穷远处边界条件为

由于核废物衰变产生的热流量对地表和地下足够深处的温度几乎不产生影响[3], 因此在z=0和z=L处, 围岩的温度分别为

1.3 解析解的推导

取

并对空间坐标z作有限傅里叶正弦变换, 控制方程(1)、初始条件(2) 和边界条件(3)、(5)～(7)分别转化为控制方程(9)、初始条件(10) 和边界条件(11)、(12):

为了将边界条件式(11) 齐次化, 根据线性微分方程解的叠加原理[15], 将(r,ω,t) 进行拆分, 即

其中,

方程(9) 化为关于θ的具有齐次边界条件的非齐次方程:

对应的初始条件式(16)、边界条件式(17) 和(18) 为

其中,

根据线性叠加原理, 设θ=θ1+θ2, 将该方程拆分为关于θ1的齐次方程和关于θ2的非齐次方程并分别求解, 边界条件形式保持不变:

对于齐次方程, 采用分离变量法求解, 设

将式(24) 代入方程(20) 并化简, 可得

通过方程(25) 可得

式中:Ji(·) 和Yi(·) 分别为i阶第一类贝塞尔函数和i阶第二类贝塞尔函数.

将解(26) 代入边界条件(22)、(23) 可得

为使A1m和B1m有非零解, 系数行列式应满足

由此可求得特征值βm, 每个特征值对应的A1m和B1m的比例为(Y1(βma),-J1(βma)).代入初始条件式(21) 可得

式(34) 左右两边同乘以

并在(a,c) 上对r积分, 利用贝塞尔函数系权重为r的正交性, 不同特征值对应的贝塞尔函数系在作用半径范围内(a ～c) 积分为0, 可得

代入式(31) 求得B1m便得到了θ1的表达式.

对于非齐次方程, 可以通过冲量定理法将其转换为具有非零初始条件和齐次边界条件的齐次方程, 令=t-τ, 取

非齐次方程转换为

对应的初始条件为

得到υ2的齐次方程通过分离变量法求解, 再代入式(38) 可以求得θ2. 根据求得的θ1和θ2,可以得到围岩的温度解析解

2 模型的验证

2.1 相关参数的确定

2.1.1 几何参数

参考芬兰KBS-3V 型处置库的概念设计,确定模型的几何参数[14]: 废物罐半径取0.525 m,高度取5.25 m, 废物罐埋置深度为500 m, 处置库的模型最大深度L取1 000 m. 具体的几何参数数值如表1 所示.

表1 几何参数数值Table 1 Geometric parameter values

2.1.2 热学参数

Kukkonen[16]对位于芬兰奥尔基洛托的处置库内花岗岩的热学参数进行了研究, 围岩的导热系数随着温度的升高逐渐减小, 在22、60 和100°C 时分别为2.70、2.61 和2.50 W/(K·m),考虑最不利的情况, 取围岩的导热系数为2.50 W/(m·K). 围岩的比热容随着温度的升高逐渐增大, 在22、60 和100°C 时分别为737、784 和832 J/(K·kg), 同样根据最不利情况, 围岩比热容选取为832 J/(K·kg). 围岩的密度统一确定为2 630 kg/m3. 处置库的地表温度为4.5°C,地温梯度为0.015°C/m. 各项热学参数数值如表2 所示.

表2 热学参数数值Table 2 Thermal parameter values

2.1.3 核废物衰变参数

由于计算模型的边界条件(3) 中包含衰变热的函数, 故通过明确废物罐内核废料的类型、体积和冷却时间来确定处置后废物罐的发热功率. 以欧洲提出的第三代原子能反应堆(evolutionary power reactor, EPR) 为例, 在不同的燃烧值和冷却时间条件下, 核废料衰变参数如表3 所示[17].

表3 不同燃烧值和冷却时间下核废料的衰变参数Table 3 Decay parameters for nuclear waste with different combustion values and cooling times

本工作的计算模型选取燃烧值为40 MW·d/(kgU)、冷却时间为40 年的EPR 型核废料,单罐核废料的重量为2.12 t,查阅表3 可得对应的衰变热功率为777 W/tU,侧面积与总表面积之比为0.91, 上述3 者相乘可得侧表面初始热功率为1 499 W. 同时由表3 可得a1=0.069 1,a2=-0.012 3,a3=1.504 8,a4=-1.396 5,a5=0.834 9.

2.2 轴对称2 维半解析解

Zhou 等[5]建立了处置库轴对称2 维3 层模型, 分析了处置库的温度场演化规律. 该模型考虑了膨润土块层、膨润土颗粒层和围岩的3 层传热结构:

图3 为该模型示意图, 图中分别给出了膨润土块层和围岩的温度场拉普拉斯域解.

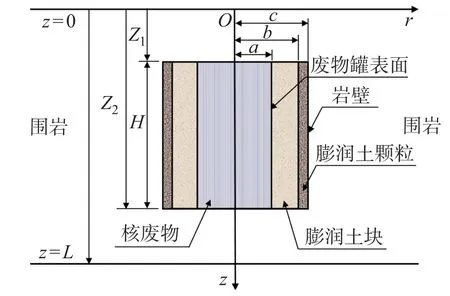
图3 轴对称2 维3 层模型示意图Fig.3 Schematic diagram of axisymmetric two-dimensional three-layer model

2.3 线热源解

H¨okmark 等[3]建立了线热源模型, 对芬兰和瑞典的处置库进行热分析, 将废物罐简化为线热源, 没有考虑缓冲材料与围岩热扩散系数差异的影响. 图4 为该线热源模型的示意图, 围岩内任意一点的温度表达式为

图4 线热源模型示意图Fig.4 Schematic diagram of linear heat source model

式中:TR(r,z,t) 为围岩的温度;z0为围岩内任意点距线热源中心点的垂直距离; erf(·) 为误差函数.

2.4 不同模型的对比验证

将表1～3 的参数代入本轴对称2 维传热模型的解析解, 即可得到处置库内任意一点的围岩温度, 为验证本模型的可靠性及结果的准确性, 计算距离废物罐轴线0.875 m 位置处的围岩温度, 并与Zhou 等[5]的轴对称2 维3 层半解析解和H¨okmark 等[3]的复合线热源解进行对比,结果如图5 所示. 对比发现所选位置的围岩温度增量与半解析解和线热源解结果接近, 均在第3 年取得峰值温度且分别为29.13、28.96 和29.42°C, 验证了本模型的可靠性以及对应解析解的准确性.

图5 不同解的温度增量对比图Fig.5 Comparisons of temperature increments from different solutions

3 废物罐罐面温度

3.1 废物罐罐面温度计算模型

由于实际的处置库中废物罐与围岩之间存在缓冲材料, 缓冲材料的导热系数要小于围岩的导热系数, 故在计算废物罐表面的温度时应当考虑缓冲层对于热传导的阻滞作用. 根据瑞典KBS-3V 处置库概念设计, 废物罐与围岩之间存在2 层缓冲材料(膨润土块层和膨润土颗粒层), 本模型厚度分别取0.30 和0.05 m. 废物罐罐面温度即为岩壁温度、膨润土块层温差与膨润土颗粒层温差之和. 利用图3 所示的3 层模型, 废物罐半径为a=0.525 m, 膨润土块层外边缘与废物罐轴线距离为b= 0.825 m, 膨润土颗粒层外边缘与废物罐轴线距离为c= 0.875 m.假设废物罐与膨润土块层、膨润土块层与膨润土颗粒层、膨润土颗粒层与围岩之间均不存在施工空隙.

3.2 单废物罐表面温度的确定

上述计算模型可以求得围岩任意时间任意位置的温度, 只需计算出缓冲层的内外温度差即可求得废物罐表面的温度, 膨润土块层任意半径处的热流量为

式中:qB(r,t) 为膨润土块层任意时间任意半径处的热流量;q(t) 为核废物罐罐面的热流量;A为核废物罐的侧面积;r为废物罐附近膨润土块层任意一点到核废物罐轴线的距离;φ为核废物罐侧面积与总表面积之比;P(t) 为核废物的衰变热功率. 核废物罐附近的膨润土块层的温度梯度表达式为

式中:λB为膨润土块层导热系数;TB(r,t) 为膨润土块层的温度. 将式(46) 代入式(48) 后, 等式两边对r进行积分, 可得膨润土块层内外边缘的温差为

同理可得, 膨润土颗粒层内外边缘的温差为

通过式(49)、(50) 与膨润土颗粒层接触的岩壁温度即可求出废物罐表面的温度:

3.3 单废物罐近场温度分布

根据3.1 节建立的模型, 可得到处置库任意位置的温度, 膨润土颗粒层与膨润土块层的温差计算参数如表4 所示. 废物罐罐面温度、膨润土块层与颗粒层交界面温度以及膨润土颗粒层与围岩交界面温度随时间的变化关系如图6(a) 所示. 图中, 各交界面的温度在前2 年快速上升并于第2 年达到峰值, 之后随着处置时间缓慢下降, 到1 000 年后温度基本不再改变,不同半径处各交界面的温度变化趋势基本一致. 在如图6(a) 所示的热演化过程中膨润土块层与膨润土颗粒层的温差较为接近, 这是由于虽然膨润土块层厚度(0.30 m) 大于膨润土颗粒层厚度(0.05 m), 但是膨润土颗粒层的导热系数(0.19 W/(m·K)) 小于膨润土块层的导热系数(1 W/(m·K)), 因此式(42) 与(43) 所得结果相近.

表4 缓冲材料计算参数Table 4 Calculation parameters of buffer material

图6 废物罐近场温度Fig.6 Near field temperatures of waste canisters

经过10 年处置后各交界面不同深度处的温度如图6(b) 所示. 当半径相同时, 核废物罐中部的温度最高, 罐体高度范围内的温度大致沿废物罐水平中轴线对称分布, 且沿深度呈现较大的温度梯度, 各交界面同一深度的温度梯度基本相同.

废物罐近场不同半径处的温度分布如图6(c) 所示. 从图中可以看到, 膨润土块层和膨润土颗粒层沿半径方向存在较大的温度梯度且膨润土颗粒层的温度梯度远大于膨润土块层和围岩, 这是由于膨润土颗粒层的导热系数远小于围岩和膨润土块层, 对废物罐衰变热的传导起到了较强的阻滞作用. 随着半径的增大, 围岩内的温度变化趋于平缓.

4 核废物罐罐面温度影响因素分析

4.1 材料热参数

4.1.1 缓冲材料导热系数

膨润土由于其较低的渗透性, 对核素有较强的吸附性以及较好的力学性能, 故被选为处置库的缓冲材料, 但其热导性能比围岩较低, 图7 和8 分别给出了5 种不同的膨润土块层导热系数(0.40、0.60、0.80、1.00 和1.20 W/(m·K)) 和5 种不同的膨润土颗粒层导热系数(0.15、0.19、0.23、0.27 和0.31 W/(m·K)) 对废物罐罐面温度的影响. 图7 的峰值温度分别为107.99、92.70、85.06、80.49 和77.49°C, 均在前2 年出现. 如图8 所示的峰值温度分别为85.74、80.49、77.12、74.61 和72.98°C. 废物罐罐面温度随着缓冲材料导热系数的增大而下降, 且膨润土块层导热系数对温度的影响更大, 这是由于膨润土块层厚度比颗粒层厚度大. 为了提高缓冲材料的散热性能, 避免废物罐罐面和缓冲材料内温度过高, 还可以通过添加碳纳米管、氧化铜等不同材料在安全基础上提高其导热性能[18].

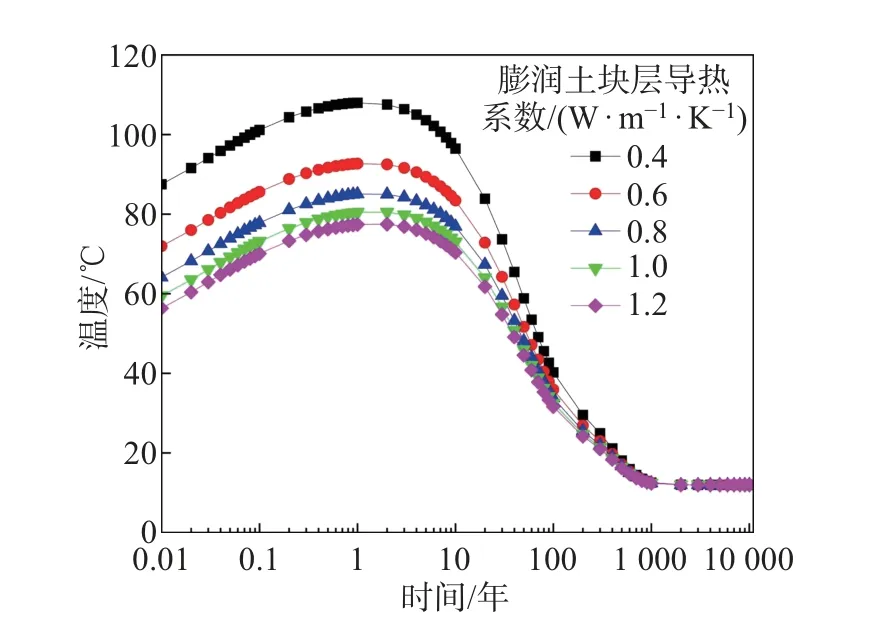
图7 膨润土块导热系数对废物罐罐面温度的影响Fig.7 Effect of thermal conductivity of bentonite block on temperature of waste canister surface

4.1.2 围岩导热系数

图9 给出了5 种不同的围岩导热系数(2.1、2.3、2.5、2.7、2.9 W/(m·K)) 对废物罐罐面温度的影响. 废物罐罐面温度随着围岩导热系数的增大而下降. 废物罐罐面的峰值温度分别为86.41、83.20、80.49、78.22 和76.28°C, 均出现在前2 年. 而实际的处置库围岩不是理想的完全密实体, 会存在许多裂缝、孔隙和沉积物, 还会因分化和侵蚀等导致其导热系数不均匀. 因此, 围岩的导热系数的选择应综合考虑各种因素, 如围岩的类型、施工的扰动以及地下水的情况等.

图9 围岩导热系数对废物罐罐面温度的影响Fig.9 Effect of thermal conductivity of surrounding rock on surface temperature of waste canister

4.2 几何参数

由于处置库内的缓冲材料很大程度上决定了处置库的温度, 且这些材料影响废物罐核素扩散的安全性, 因此有必要对缓冲材料的几何参数进行研究. 图10 和11 分别给出了5种不同的膨润土块层厚度(0.1、0.2、0.3、0.4 和0.5 m) 和5 种不同的膨润土颗粒层厚度(0.01、0.03、0.05、0.07 和0.09 m) 对废物罐罐面温度的影响, 由图中可见温度均随着缓冲材料厚度的增大而下降. 图10 中的峰值温度分别为74.80、77.85、80.49、82.89 和85.12°C, 图11 中的峰值温度分别为66.06、73.36、80.49、87.57 和94.53°C. 膨润土颗粒层厚度的变化对于废物罐罐面温度变化的影响比膨润土块层大, 这是由于膨润土颗粒层的导热系数比膨润土块层导热系数小得多, 厚度的改变更能影响热流量的传导. 因此, 应当综合考虑废物罐温度的安全性, 对于地下水渗流以及核素迁移的限制作用, 选取合适的缓冲材料厚度.

图10 膨润土块层厚度对废物罐罐面温度的影响Fig.10 Effect of bentonite block layer thickness on surface temperature of waste canister

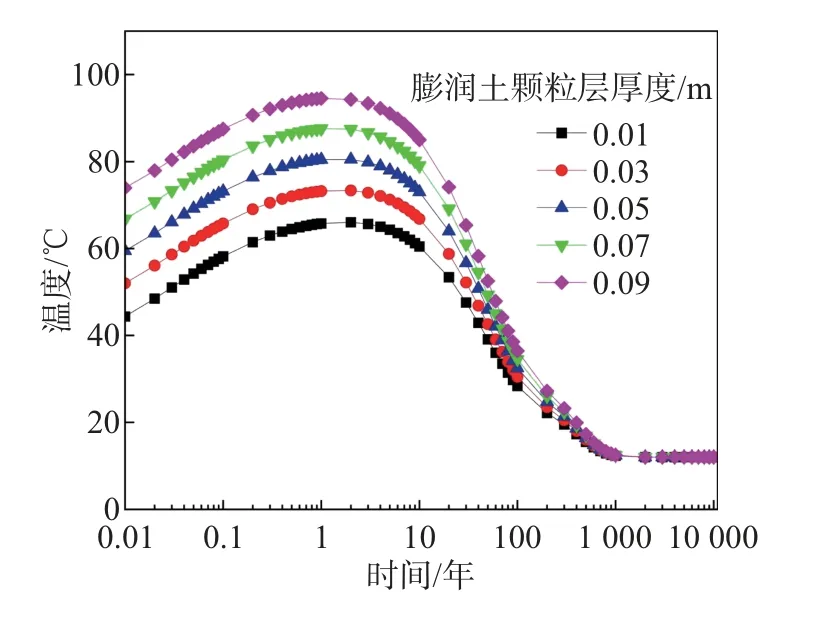
图11 膨润土颗粒层厚度对废物罐罐面温度的影响Fig.11 Effect of bentonite granular layer thickness on surface temperature of waste canister

4.3 核废物衰变参数

4.3.1 核废物冷却时间

图12 给出了燃烧值为40 MW·d/(kgU) 的EPR 核废物分别在20、40、60 年的冷却时间条件下对废物罐罐面温度的影响. 从图中可见, 冷却时间越久, 处置后核废物罐罐面峰值温度越低, 峰值温度分别为108.69、80.49 和62.76°C, 较长的冷却时间可以较大程度地降低核废物罐入库后的峰值温度, 故从安全性的角度考虑, 在核废物入库前应根据预设的温度阈值来确定核废物的冷却时间.

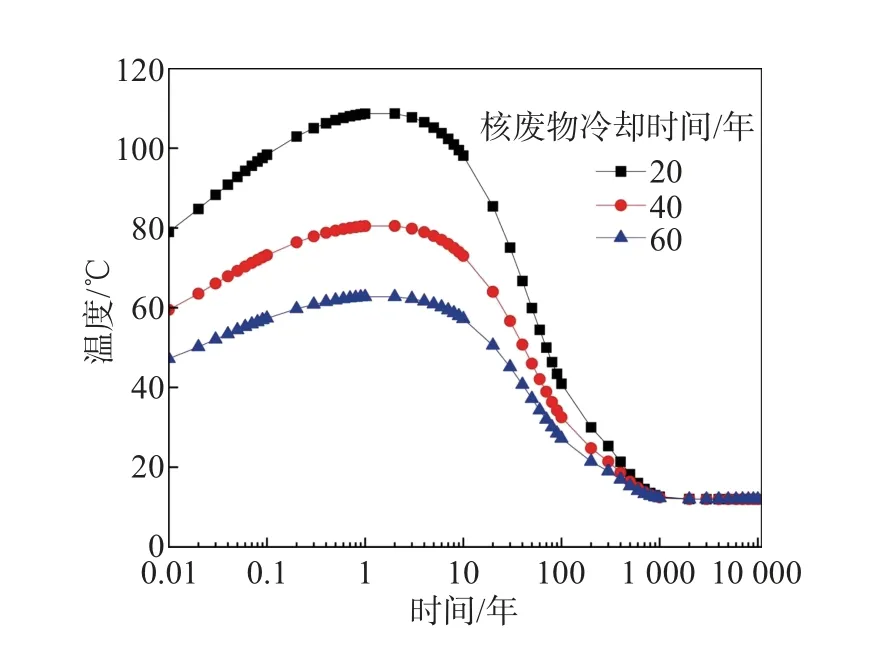
图12 核废物冷却时间对废物罐罐面温度的影响Fig.12 Effect of cooling time of nuclear waste on surface temperature of waste canister

4.3.2 核废物燃烧值

图13 给出了冷却时间为40 年时, 燃烧值分别为40、50、60 MW·d/(kgU) 对EPR 核废物温度的影响. 随着核废物燃烧值的上升, 废物罐罐面温度呈上升趋势, 峰值温度分别为80.49、100.60 和122.26°C, 燃烧值为50、60 MW·d/(kgU) 时罐面峰值温度超过了100°C, 故应考虑通过减少单废物罐内核废物的量或者增加核废物的冷却时间来避免过高的温度影响处置库的安全.

图13 核废物燃烧值对废物罐罐面温度的影响Fig.13 Effect of combustion value of nuclear waste on surface temperature of waste canister

5 结 论

(1) 根据瑞典KBS-3V 处置库概念设计, 本工作建立了一个单废物罐轴对称2 维传热模型, 利用有限傅里叶正弦变换、分离变量法等解析方法得到了处置库温度场演化的解析解, 并与已有的半解析解和复合线热源解进行对比, 峰值温度增量均在第2 年出现, 分别为29.42,29.13 和28.96°C, 证明了本解析解的正确性.

(2) 本工作建立了一个包含膨润土块层、膨润土颗粒层以及围岩的3 层热分析模型, 采用在岩壁温度上叠加缓冲层温度差的方法得到废物罐表面以及近场缓冲层的温度, 并分析了废物罐近场温度随时间、深度和半径的变化规律, 发现废物罐表面温度于第2 年到达峰值, 其中部温度最高(80.49°C), 缓冲材料内有较大的温度梯度而围岩内的温度梯度较小.

(3) 本工作研究了不同材料的热参数、几何参数和核废物衰变参数对废物罐罐面温度的影响. 研究发现, 缓冲材料和围岩导热系数越大、缓冲材料厚度越小、核废料燃烧值越小、冷却时间越长都会使废物罐罐面温度变小. 膨润土块层的导热系数对温度的影响比膨润土颗粒层大, 膨润土颗粒层的厚度对温度的影响比膨润土块层大.

本工作建立的数学模型得到的解析解可以快速得到处置库内任意深度、半径、时间的温度值, 为后续的研究以及处置库的安全设计提供参考.