双层锥形非粘结隔震支座力学模型及地震响应分析

郝瑞康, 何文福, 张 强, 陈睦锋

(上海大学力学与工程科学学院, 上海 200444)

减隔震技术起源于20 世纪, 经过几十年的发展已经日趋成熟. 隔震技术的基本原理主要是通过在结构物的基底设置隔震支座, 使结构物与地基中的基础顶面分离, 从而减少地震动向结构物的传递[1]. 随着我国抗震设防要求的提高, 高烈度区所占国土面积的比例也随之增大[2].其中我国村镇民用建筑占有较大比例, 但是大部分村镇建筑造价较低, 基本未考虑抗震设防.隔震技术作为重要的抗震手段, 能在不改变主体结构的同时有效提高建筑物抗震性能. 但是,传统的叠层橡胶隔震支座自重大、制作工艺复杂且造价高昂, 不适合大规模应用于我国村镇地区, 因此有必要研发出一种适用性更广泛的简易支座.

对于简易隔震支座, 已有大量专业人员进行了研究. 谭平等[3]提出了一种采用工程塑料板橡胶隔震支座的新型简易隔震支座, 该支座将不饱和聚酯纤维加强复合材料板替代普通橡胶支座中的钢板,具有重量轻、造价低、运输与施工方便、适用于低矮村镇建筑等优点. 田湾[4]开发了一种适合于高烈度寒冷地区村镇建筑的简易复合隔震体系, 该隔震体系通过在建筑基底设置砂隔震垫层, 同时在圈梁之间铺设摩擦滑移材料进行隔震; 徐凯等[5]研究分析了选用2 类不同的复合材料来替代传统橡胶支座中的钢板而形成的简易隔震支座; 卜长明[6]针对砌体结构提出了沥青-砂垫层消能减震技术和捆绑橡胶束消能减震技术这2 种简易消能减震技术; 代宇飞[7]研究了一种针对新疆村镇地区的单层复合隔震体系模型; 袁康等[8]针对村镇底层砌体建筑提出了一种在圈梁内布置橡胶束的新型简易滑移隔震体系; 何文福等[9]提出了一种锥形非固结隔震支座, 并对其进行了参数试验分析; 黄思洋[10]提出了一种十字卡槽式简易隔震支座; 李英民等[11]研究了在村镇建筑中应用滑移隔震技术的有效性和可行性; 钱国桢等[12]对改性沥青阻尼垫与约束砂垫层这2 种隔震方法进行了对比分析; 赵少伟等[13]探讨了粒径砂垫层在不同厚度下的隔震效果; 张超等[14]研究了橡胶粉的静等效刚度、吸能能力、进入隔震区频率点和隔震传递率随着目数、堆积厚度和承载重量变化的规律, 为橡胶粉隔震垫的设计提供了依据; Tsang 等[15-16]提出了废旧轮胎橡胶-土混合隔震层, 该方法可同时降低水平向和竖向地震响应; Fakhouri 等[17]提出了一种经济高效的提升滑动支座, 并介绍了其工作原理, 由于几何构造的独特性, 故在减小水平位移上具有很大潜力; Nanda 等[18]研究了土工布作为摩擦滑移材料在地震作用下的耗能效果.

为解决广大高烈度地区村镇房屋抗震能力不足的问题, 新型的减隔震技术已受到研究人员广泛关注, 但目前还缺乏能兼顾隔震减震性能、超设计地震限位功能、施工安装实用性和经济性的装置. 本工作提出了一种双层锥形隔震支座, 具有造价低廉、制作工艺简单的特点; 推导出了支座水平刚度的计算公式, 对可能影响支座耗能能力的各因素进行了参数分析; 利用有限元软件对采用双层锥形隔震支座的结构进行了结构响应分析, 验证了所提出的支座对结构的隔震效果.

1 双层锥形隔震支座构造及理论

双层锥形隔震支座由上凹盖板、下凸盖板、夹层钢板、橡胶层组成, 上下橡胶层为同种材料且厚度相同, 支座示意图如图1 所示. 橡胶层与上下盖板、夹层钢板均无粘结. 当发生地震时, 支座通过橡胶层与夹层钢板的相互运动来减小刚度消耗能量, 从而达到隔震的目的.

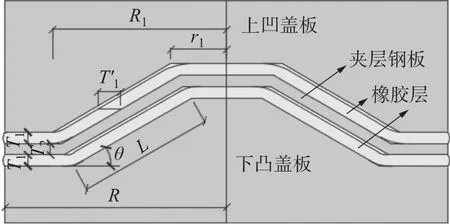
图1 锥形固结支座示意图Fig.1 Schematic diagram of the conical consolidation bearing

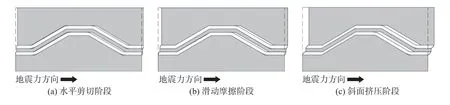
图2 支座运动状态示意图Fig.2 Schematic diagram of the movement state of the bearing

图1 中,R为支座半径;R1为上凹盖板除去外侧圆环剩余部分的半径;r1为上凹盖板内部圆底部分半径;T1为橡胶层厚度;T2为夹层钢板厚度;为橡胶层在斜面部分的水平长度;L为倾斜橡胶层沿斜面的母线长度;θ为支座倾斜角度

1.1 运动状态

双层锥形隔震支座在水平地震力作用下将发生相对位移. 本工作根据相对位移大小, 将其分为3 个运动状态: 水平剪切阶段、滑动摩擦阶段和倾斜橡胶层挤压阶段(见图1).

第一个运动状态为支座在水平地震力作用下开始运动, 此时橡胶层受到水平剪切力作用,开始做水平剪切运动, 当支座的整体相对位移等于橡胶层的整体水平剪切极限位移之和时, 第一个运动状态结束, 在这一状态下支座通过橡胶层的剪切变形耗能; 第二个运动状态从支座水平橡胶层达到水平剪切极限位移后发生滑动摩擦开始, 直到上凹盖板与夹层盖板的斜面均与倾斜橡胶层开始接触, 在这一状态下支座主要通过克服摩擦力耗能, 橡胶层不产生变形; 滑动摩擦阶段结束后支座对斜面橡胶作水平挤压运动, 2 层橡胶随着盖板的水平运动而产生变形,此为第3 个运动状态. 当橡胶层达到最大水平变形后第3 个运动状态结束, 在这一状态下支座通过橡胶垫的挤压变形耗能.

1.2 水平剪切状态下刚度公式

根据支座在水平地震力作用下的运动状态, 推导出各阶段的刚度公式, 得到其本构关系.

水平剪切阶段, 钢板与橡胶接触面为静摩擦力, 且上下橡胶层为同种材料且厚度相同, 因此剪切模量及剪切极限位移均相同.

当支座进入水平剪切阶段时, 上下2 层橡胶同时开始运动且同时达到水平剪切极限位移,此时可等同普通橡胶支座. 当考虑第1 层橡胶(自上而下) 单独工作时, 支座水平刚度为[19]

式中:G为橡胶剪切模量;T1为橡胶层厚度;A1为第1 层橡胶(自上而下) 与支座盖板的水平接触面积, 其中

式中:R为锥形支座半径;R1、r1见图1 所示, 整理得第一阶段支座水平刚度:

当考虑第2 层橡胶(自上而下) 单独工作时, 支座水平刚度为

式中:T2为夹层钢板厚度;

1.3 滑动摩擦状态下刚度公式

当上下水平橡胶层在水平地震作用下同时达到剪切极限位移后, 支座上凹盖板与夹层钢板开始在橡胶层上发生滑动, 此时滑动摩擦力Fmax开始做功,

式中:μ为盖板与橡胶的摩擦系数;N为支座所受竖向力.

1.4 斜面挤压状态下刚度公式

当在水平地震作用下完成滑动摩擦阶段后, 支座上下盖板及夹层钢板开始压剪2 层橡胶层的斜面部分.

第1 层斜面橡胶在地震力作用下最大水平位移为δ01, 则斜面橡胶圆周上其他受挤压点的水平变形量近似为

式中:φ为斜面橡胶圆周上其他受挤压点和圆心所连的直线与运动方向之间的夹角(见图3),且0＜φ ＜π/2. 单层倾斜橡胶的水平长度为

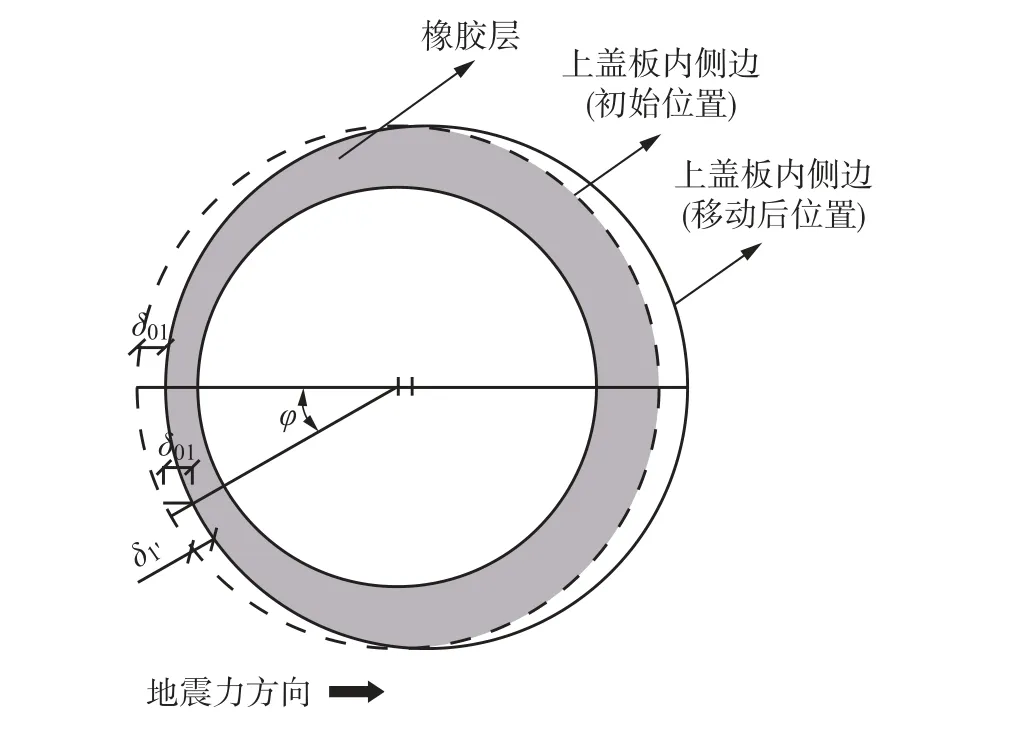
图3 支座橡胶层水平剖面示意图Fig.3 Horizontal sectional view of the rubber layer of the bearing

倾斜橡胶层沿斜面的母线长度为

被挤压的斜面橡胶层法向应力为

为第1 层斜面橡胶压缩面积, 由几何关系可得出:

取上一个面积微元, 则该无穷小面积d上的法向力为

则与水平地震力平行方向的作用力为

对其进行积分, 得出该阶段的刚度为

第2 层斜面橡胶挤压时的刚度公式为

1.5 支座整体运动刚度公式

该支座为双层橡胶, 每一层橡胶均考虑3 个运动阶段, 那么针对支座整体也是3 个运动阶段, 即水平剪切、滑动摩擦和斜面压剪. 每个阶段上下2 层橡胶层同步运动, 也即同时发生水平剪切、滑动摩擦、斜面压剪. 支座在每个阶段的刚度可由相应状态下单层橡胶刚度求得,由式

可得, 水平剪切阶段支座整体刚度为

斜面挤压阶段支座整体刚度为

支座的理论滞回曲线如图4 所示.

图4 支座理论滞回曲线Fig.4 Theoretical hysteresis curves of the bearing

2 单层锥形隔震支座数值模拟及试验验证

在得出了双层锥形隔震支座的刚度公式后, 当锥形隔震支座为单层橡胶时, 其2 个阶段刚度公式为式(3) 和(14). 从刚度公式中可以看出, 支座的橡胶层厚度及倾斜角度是影响锥形支座耗能的关键因素. 本工作采用Abaqus 有限元软件对单层锥形隔震支座进行模拟, 分析上述2 个因素对其耗能能力的影响, 为验证支座数值模型可靠性, 刘文光等[20]对支座进行相应工况数值模拟.

2.1 有限元模型

为研究橡胶材料厚度及倾斜角度对支座耗能能力的影响, 在Abaqus 有限元软件中建立了倾斜角度分别为30°、45°、60°的3 组支座, 橡胶材料厚度分别设计有8 和10 mm. 以倾斜角度为30°、橡胶材料厚度为10 mm 支座为例, 详细尺寸如图5 所示. 有限元模拟各试验工况如表1 所示.

表1 有限元模拟各试验工况Table 1 Various test conditions of finite element simulation

图5 单层锥形隔震支座尺寸(mm)Fig.5 Size of single-layer conical isolation bearing (mm)

针对单个支座建模, 首先在软件中建立上凹盖板、下凸盖板和橡胶层的部件, 将材料的力学性能赋予到各自对应的部件, 橡胶材料采用Mooney-Rivlin 模型[21]. 之后, 将其装配成单层锥形隔震支座, 在各部件接触面建立摩擦相互作用. 接着对隔震支座进行边界条件和荷载分析步的设置: 将支座底面进行固定处理, 限制支座底面x、y、z3 个方向的自由度; 对支座进行压剪试验, 在其上表面施加相应的竖向荷载, 此为第1 个分析步; 对支座上凹盖板施加水平位移荷载, 此为第2 个分析步. 对隔震支座进行网格划分, 上凹盖板、下凸盖板选用C3D8R 单元,橡胶层选用C3D8RH 单元, 工况1 所用有限元模型如图6 所示.

图6 支座有限元模型Fig.6 Finite element model of bearing

2.2 试验验证

图7 为各工况试验与模拟结果对比. 从图中可以看出, 模拟所得的支座的力-位移曲线与试验所得数据曲线均呈现双锥形的特性, 曲线趋势大致相同. 在支座倾斜角度较小时, 理论曲线与试验曲线吻合较好, 各阶段刚度变化趋势与预期一致; 在支座倾斜角度较大时, 斜面压剪阶段的尖角段有所差别, 最大水平反力均相同.

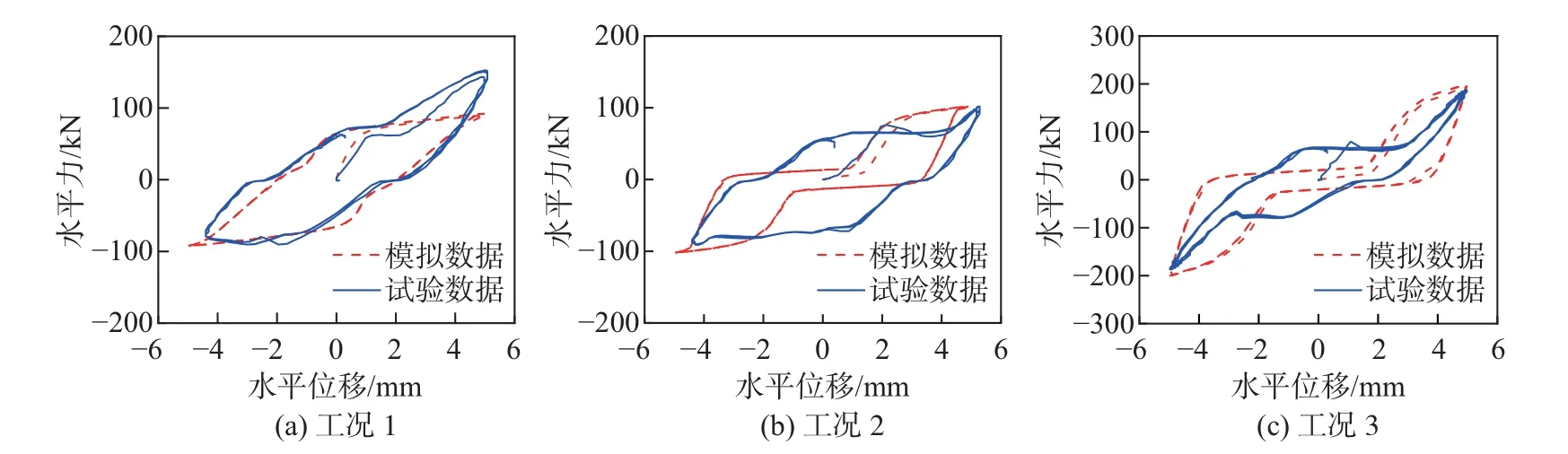
图7 各工况试验与模拟结果对比Fig.7 Comparisons of test results and simulation results under various working conditions

3 双层锥形隔震支座参数分析

由上述支座整体刚度公式可看出, 双层锥形隔震支座的刚度主要与支座的倾斜角度、橡胶材料厚度有关, 因此采用Abaqus 有限元软件建立不同倾斜角度及橡胶材料厚度组合的支座模型, 分析其在不同竖向压应力及水平位移下的刚度及耗能能力. 双层锥形隔震支座直径为390 mm, 支座有限元模拟工况如表2 所示.

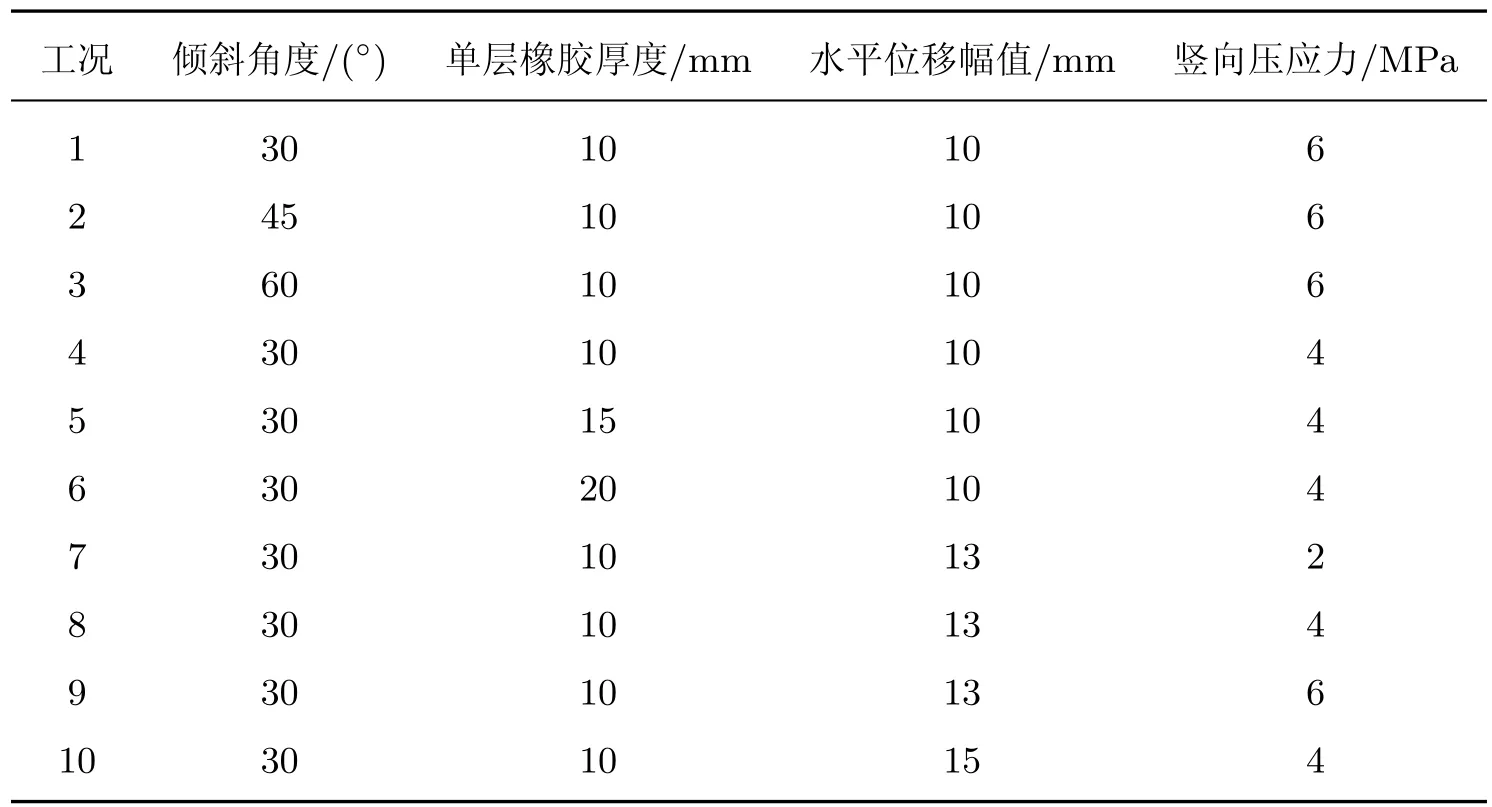
表2 支座有限元模拟工况Table 2 Finite element simulation condition of bearing

3.1 不同倾斜角结果对比

以不同倾斜角度进行对比试验, 双层锥形隔震支座橡胶材料厚度采用单层10 mm, 水平加载位移10 mm, 竖向压应力6 MPa, 分别在30°、45°、60°这3 种不同倾斜角度进行分析, 滞回曲线如图8(a) 所示.

图8 各工况试件滞回曲线对比Fig.8 Comparisons of hysteresis curves of specimens under various working conditions

从图8(a) 可以看出, 倾斜角度为30°的支座试件所形成的滞回环面积最大, 压剪阶段所形成的尖角最饱满; 倾斜角度为60°的支座试件所形成的滞回环面积最小, 压剪阶段所形成的尖角较窄; 倾斜角度为90°时支座滞回曲线的双锥形最为明显. 可见, 在相同橡胶材料厚度和加载情况下, 倾斜角度越小其耗能能力越大, 压剪阶段的水平刚度也随倾斜角度增大而减小.

图9(a) 为支座在不同倾斜角度下的等效刚度与等效阻尼. 从图中可以看出, 倾斜角度增大, 支座等效刚度增大; 倾斜角度增大, 支座等效阻尼先增大后减小.

图9 各工况试件等效刚度与等效阻尼Fig.9 Equivalent stiffness and equivalent damping of specimens under various working conditions

3.2 不同橡胶层厚度结果对比

以不同橡胶材料厚度进行对比试验, 双层锥形隔震支座倾斜角度设为30°, 水平加载位移10 mm, 竖向压应力4 MPa, 分别在橡胶材料单层厚度为10、15 和20 mm 进行分析. 滞回曲线如图8(b) 所示.

由图可知, 在支座倾斜角度和加载位移相同时, 使用不同厚度橡胶层的试件所形成的滞回曲线面积随厚度增大而有所增大; 水平剪切阶段的刚度略有差异, 斜面压剪阶段的刚度随厚度增大而减小.

图9(b) 为支座在不同橡胶层厚度下的等效刚度与等效阻尼. 从图中可以看出, 橡胶层厚度增大, 支座等效刚度减小, 等效阻尼增大.

3.3 不同竖向压应力结果对比

针对不同竖向压应力进行对比试验, 双层锥形隔震支座倾斜角度设为30°, 单层橡胶层厚度为10 mm, 水平加载位移为10 mm, 分别针对竖向压应力为2、4 和6 MPa 进行分析, 滞回曲线如图8(c) 所示.

由图可知, 在加载位移相同时, 随着竖向压应力的增大, 所围成滞回环整体形状变得更加尖锐, 即斜面压剪阶段的尖角更为明显. 不同压应力下的最大摩擦力增大比例与应力增大比例不同, 原因是橡胶材料与盖板之间的摩擦系数会随着竖向压应力变化.

图9(c) 为支座在不同竖向压应力下的等效刚度与等效阻尼. 从图中可以看出, 竖向压应力增大, 支座等效刚度增大, 等效阻尼先增大后减小.

3.4 不同加载位移结果对比

针对不同加载位移进行对比试验, 双层锥形隔震支座倾斜角度设为30°, 单层橡胶材料厚度为10 mm, 竖向压应力为4 MPa, 分别针对水平加载位移10、13 和15 mm 工况进行数值分析, 滞回曲线如图8(d) 所示.

从图中可以看出水平加载位移越大, 滞回曲线所围成的面积越大, 试件耗能性能越好, 但加载位移的变化对滞回曲线的影响稍小.

图9(d) 为支座在不同水平加载位移下的等效刚度与等效阻尼. 从图中可以看出, 水平加载位移增大, 支座等效刚度增大, 等效阻尼先增大后减小.

4 隔震结构地震响应分析

4.1 有限元算例

为研究双层锥形隔震支座的隔震效果, 应用有限元软件对双层锥形隔震结构进行结构响应分析, 计算双层锥形隔震结构与原结构的加速度响应、层间剪力与层间位移.

以一栋3 层基础隔震的钢筋混凝土框架结构为例, 在基础层设置双层锥形隔震支座. 该结构的抗震设防烈度为8 度, 设计基本加速度为0.2 g, 场地类别为Ⅲ类. 结构立面图如图10 所示, 总高为9.3 m, 底层层高3.3 m, 标准层高3 m, 总重为743 t. 选用2 条天然波(Landers、Cape) 和1 条人工波(RH1) 进行地震动分析. 按照8 度设防水准进行加载(对应峰值加速度为0.2 g).x方向与y方向的输入峰值之比为1∶1.

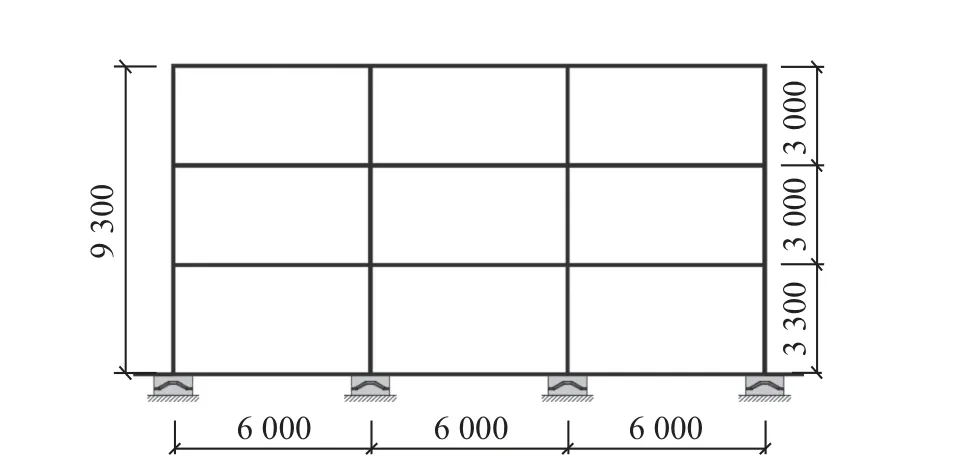
图10 结构立面图(mm)Fig.10 Elevation view of the structure (mm)

为分析研究双层锥形隔震支座不同倾斜角度及不同橡胶层厚度对结构响应的影响, 故当设置倾斜角度为30°时, 单层橡胶层厚度分别为10、15 和20 mm 的3 组支座; 以及单层橡胶层厚度为10 mm 时, 倾斜角度分别为30°、45°和60°的3 组支座, 分析不同因素对结构的影响. 支座布置如图11 所示. 以倾斜角为30°、橡胶材料厚度为10 mm 支座为例, 详细尺寸如图12 所示.

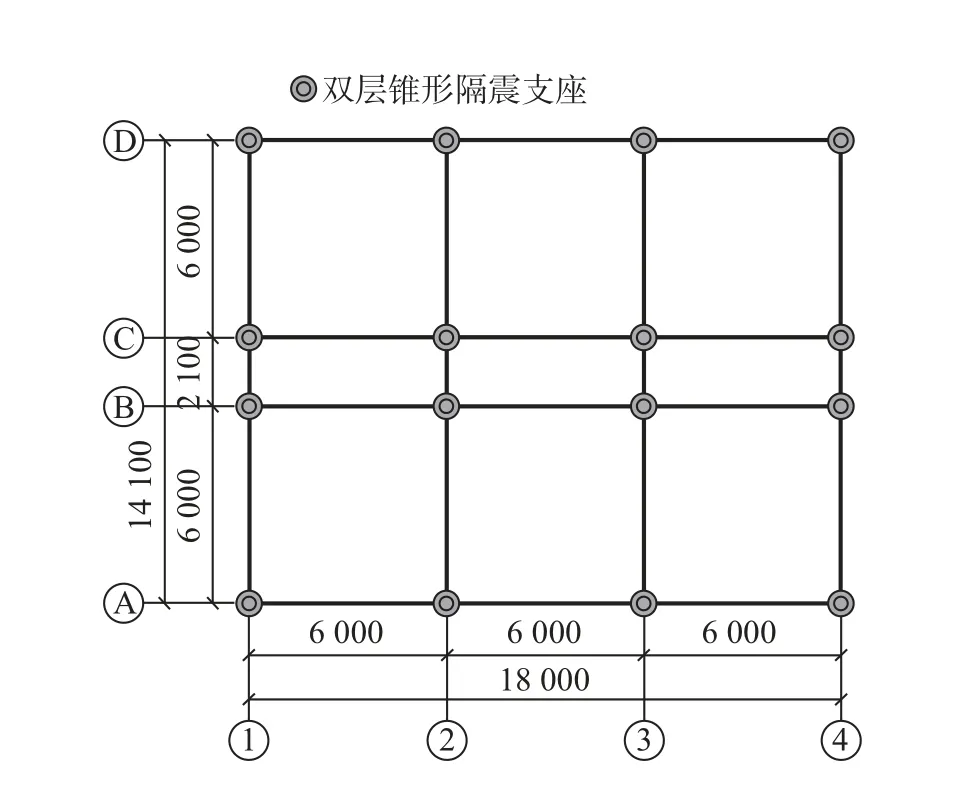
图11 支座布置图(mm)Fig.11 Layout drawing of bearing (mm)

图12 双层锥形隔震支座尺寸(mm)Fig.12 Size of double-layer conical isolation bearing (mm)

4.2 结构响应对比

双层锥形隔震结构在3 条地震波输入下的各项结构响应与原结构对比如图13、14 所示.

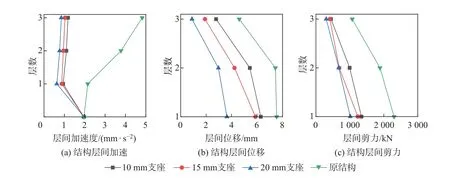
图13 不同橡胶层厚度下的结构响应Fig.13 Structural responses under different rubber layer thicknesses

图13 为支座倾斜角度为30°时, 单层橡胶材料厚度分别为10、15 和20 mm 的3 组支座所得的结构响应平均值. 从图中可以看出, 双层锥形隔震支座隔震效果明显, 且橡胶厚度越大其隔震效果越明显.

针对结构层间加速度分析, 3 组橡胶支座均使结构顶层层间加速度降低70% 左右; 针对结构层间位移分析, 结构最大层间位移角为1/524. 针对结构层间剪力分析, 3 组支座中层间剪力最少降低41%.

图14 为单层橡胶材料厚度为10 mm 时, 倾斜角度分别为30°、45°和60°的3 组支座所得的结构响应平均值. 从图中可以看出, 双层锥形隔震支座隔震效果明显, 且倾斜角度越小其隔震效果越强.

图14 不同倾斜角度下的结构响应Fig.14 Structural responses at different tilt angles

针对结构层间加速度分析, 3 组橡胶支座均使结构顶层层间加速度降低60% 以上; 针对结构层间位移分析, 结构最大层间位移角为1/506. 针对结构层间剪力分析, 3 组支座中层间剪力最少降低40%.

5 结 论

本工作对双层锥形隔震支座进行了变形理论分析及有限元模拟, 研究了双层锥形隔震支座的力学性能, 并对支座的倾斜角度、橡胶材料厚度、水平加载位移及竖向压应力对支座力学性能的影响进行了分析, 结论如下.

(1) 通过理论分析, 得到了双层锥形隔震支座的恢复力模型. 双层锥形隔震支座在运动时经历水平剪切、滑动摩擦及斜面挤压3 个阶段, 支座主要在水平剪切和斜面挤压这2 个阶段消耗能量.

(2) 支座刚度大小主要与支座橡胶材料厚度、倾斜角度有关, 通过有限元软件对单个双层锥形隔震支座进行有限元模拟可以发现: 支座倾斜角度越大, 支座第3 阶刚度越大; 橡胶材料厚度越大, 支座所形成的滞回环面积增大; 竖向压应力和水平加载位移增大, 支座耗能也有所增大.

(3) 通过对双层锥形隔震结构进行结构响应分析可见, 加支座后结构隔震效果明显, 结构顶层加速度降低60%; 隔震结构最大层间位移为1/506, 在许可范围内; 层间剪力减小了40%.