考虑界面滑移和掀起的组合梁弯曲变形解析解

杨 骁 王 欢

(1. 上海海关学院公共教学部, 上海 201204; 2. 上海大学力学与工程科学学院, 上海 200444)

通过可靠连接可使组合梁的两种材料子梁协调变形、充分发挥材料性能, 因此, 组合梁为结构工程创新和解决超高、大跨、重载、复杂结构等特殊设计难题提供了新选择, 已被国内外广泛应用[1-4]. 在实际工程中, 剪力连接件所产生的水平与竖向变形均会影响组合梁构件性能.基于此, 聂建国等[5-8]提出了抗拔不抗剪连接新技术, 为解决负弯矩区混凝土板的抗裂难题提供了新思路. 由此可知, 研究组合梁连接面滑移与掀起效应对其力学性能的影响十分重要. 目前, 连接面纵向滑移效应对组合梁力学性能影响的研究已基本成熟, 得到了众多有意义的结果. 而考虑连接面滑移与掀起共同效应对组合梁力学性能影响的研究报道则相对较少, 且已有结果大都依赖数值解法, 缺少相关的解析结果.

多年来, 国内外众多专家学者对组合梁力学性能进行了理论分析和定量化研究. 在Andreus 首次提出组合梁换算截面法的基础上, Newmark 等[9]建立了部分剪力相互作用组合梁线性弯曲的一维控制方程——Newmark 模型. 该模型只考虑了组合梁连接面间的纵向滑移, 而未考虑其竖向掀起. 肖岩等[10]利用二阶算法, 给出了若干边界条件下, 考虑连接面滑移的钢-混凝土组合梁层间滑移位移和弯曲挠度的解析解. 同时, Ranzi 等[11]、Faella 等[12]和Girhammer 等[13]在线性范围内研究了组合梁柱的刚度, 给出了连续组合梁曲率的简化计算方法. Dall′asta 等[14]、Faella 等[15]、Salari 等[16]、Fabbrocino 等[17]和Oehlers 等[18]在材料和抗剪连接件的非线性范围内分析了抗剪连接件对组合梁整体性能的影响, 分析了抗剪连接件对组合梁整体性能的影响.

然而, 上述研究只考虑了组合梁连接面间的纵向滑移, 假定了组合梁两子梁的挠度相同,并未涉及组合梁的界面掀起效应. 关于连接面滑移与掀起共同效应对组合梁力学性能的影响,Adekola[19]首次推广了Newmark 模型, 同时考虑了钢-混凝土组合梁纵向滑移和竖向掀起的效应, 并采用有限差分法数值模拟了组合梁的力学行为. Gara 等[20]给出了考虑纵向滑移和竖向掀起效应组合梁的有限元公式, 提出用具有12 自由度、14 自由度和22 自由度的3 种有限单元数值模拟组合梁的弯曲变形. Krofli 等[21]提出了线弹性组合梁应力应变状态分析的数学模型及其解析解, 并评估了横向和纵向刚度以及连接面层厚度对跨中受集中载荷的简支钉扎双层木梁性能的影响. 但该解析解存在21 个未知数, 求解过程过于复杂, 且未给出化简后微分方程的具体表示形式. 在此基础上, Krofli 等[22-23]进一步考虑了材料非线性、剪切与法向接触的非线性, 提出了几何非线性模型, 给出了基于应变的有限元数值解法. 戚菁菁等[24]研究了界面滑移、竖向掀起及剪切变形对钢-混凝土组合连续梁动力性能的影响, 数值计算了连续组合梁的动力特性和动力响应. 杨骁等[25]研究了界面掀起和轴力对组合梁动力弯曲特性的影响;基于Hamilton 原理, 建立了考虑界面掀起和轴力的组合梁非线性动力弯曲及其一阶近似控制方程, 给出了边界条件的严格提法; 首次采用微分求积法分析组合梁的自由振动与稳定性. 综上可见, 考虑界面滑移与掀起共同效应对组合梁力学性能影响的研究多为数值方法, 缺少精确的解析解.

对于新型黏结型钢-混凝土组合梁桥, Thomann 等[26-27]研究了压花钢板与水泥浆连接面的力学性能, 分析了界面滑移位移与掀起位移之间的关系, 以及连接面滑动和剪切应力的三线性关系, 但未探究界面掀起对整个梁弯曲变形的影响. 杨骁等[28-29]探究了考虑黏结层滑移效应的组合梁的弯曲, 给出了简支组合梁在均布载荷下和悬臂梁在集中力下的弯曲解析解, 但未考虑界面黏结胶的掀起效应.

基于此, 为了考虑连接面纵向滑移与竖向掀起效应, 假定组合梁两子梁变形满足Euler-Bernoulli 梁弯曲理论, 以及连接面间存在纵向和竖向分布线性弹簧. 本工作建立了以两子梁挠度和连接面滑移位移为基本未知量的组合梁动力弯曲控制方程. 利用Laplace 变换及其Laplace 逆变换, 得到了均布载荷作用下简支组合梁静力弯曲变形时子梁挠度和层间相对滑移的解析解, 进而得到组合梁的轴力与弯矩等. 在验证解析解正确性与合理性的基础上, 假定两子梁材料和几何参数相同, 重点分析了纵向和竖向分布线性弹簧刚度以及加载方式等对简支组合梁弯曲变形和内力的影响. 本工作所得到的一些有意义的结论可以为实际工程提供理论指导.

1 考虑界面滑移与掀起的组合梁控制方程

图1 为典型的组合梁模型. 该组合梁通过剪力连接件或黏结胶连接上部子梁C 和下部子梁S 而形成. 取子梁C 和子梁S 的连接面Oxy平面, 组合梁横截面的对称面Oxz平面, 建立直角坐标系Oxyz. 设组合梁长为L, 子梁C 和子梁S 的高和宽分别为hc、bc和hs、bs, 横截面积分别为Ac和As, 横截面的形心惯性矩分别为Ic和Is; 子梁C 的形心Cc和子梁S 的形心Cs到Oxy平面的距离分别为rc和rs; 子梁C 和子梁S 的弹性模量分别为Ec和Es, 密度分别为ρc和ρs. 假设在上部载荷qc(x) 和下部载荷qs(x) 作用下, 组合梁变形满足: ①子梁S和子梁C 均为线性弹性体, 满足Euler-Bernoulli 梁弯曲变形假定, 即为小挠度、小变形; ②将连接子梁C 和子梁S 的剪力连接件或黏结胶等效为分布在连接面的竖向和纵向弹簧, 记其单位长度的弹簧刚度分别为Kw和Ku.

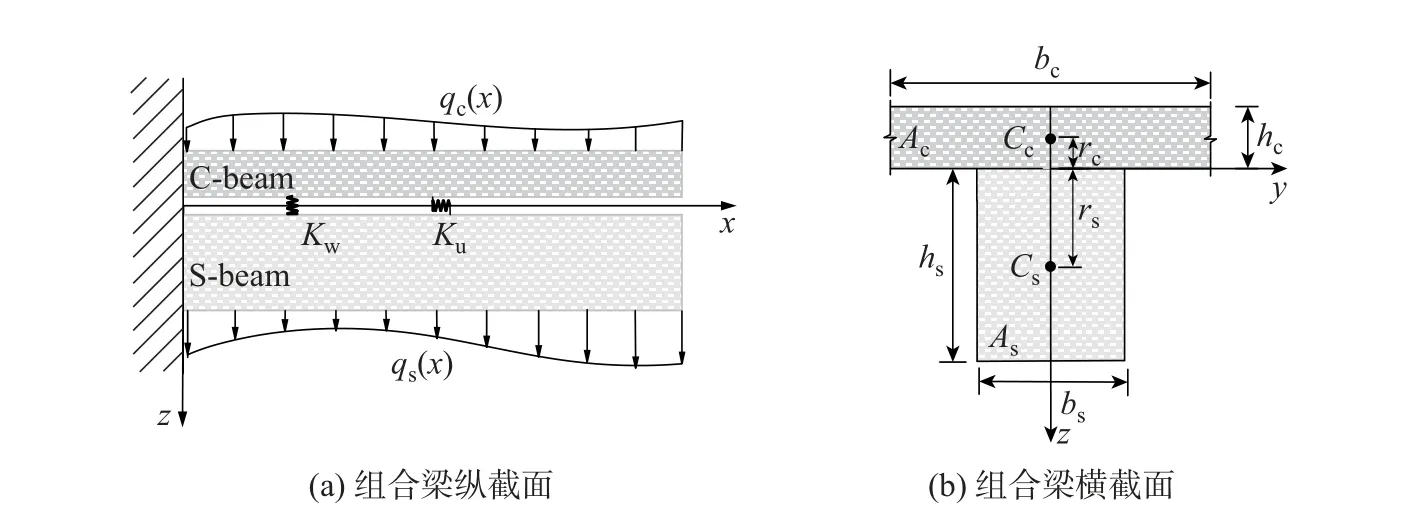
图1 典型的组合梁模型Fig.1 Models of the typical composite beam

若组合梁采用栓钉连接, 则

式中:k1和ks分别为单个栓钉的抗拔刚度和抗剪刚度[7-8];n为栓钉列数;p为栓钉纵向间距.

假设子梁C 形心轴线上任一点(x,0,-rc) 和子梁S 形心轴线上任一点(x,0,rs) 的水平位移与竖向挠度分别为uc(x)、wc(x) 和us(x)、ws(x). 根据Euler-Bernoulli 梁弯曲变形假定, 子梁C 和子梁S 上任意一点的纵向位移与竖向挠度uc(x,y,z)、wc(x,y,z) 和us(x,y,z)、ws(x,y,z) 可分别表示为

记两子梁连接面间的滑移位移和掀起位移分别为ur(x) 和wr(x), 则

由几何方程和本构方程可得, 子梁C 和子梁S 横截面上的轴力Nc、Ns和弯矩Mc、Ms可分别表示为

根据前面的假设, 两子梁连接面间的单位长度纵向剪力Tu和单位长度竖向拉力Tw分别为

对子梁C 和子梁S 分别取微元段dx, 则该微元段的受力情况如图2 所示. 由动力学方程可得:

图2 组合梁微元段dx 的受力Fig.2 Internal forces of composite beam infinitesimal element dx

将式(3) 和(4) 代入式(5) 和(6), 并消除Fc和Fs, 可得以uc、wc、us和ws为基本未知量的具有界面滑移和掀起效应的组合梁弯曲变形动力控制方程, 即

当组合梁发生静力弯曲时, 动力控制方程(7) 可进一步退化为静力弯曲控制方程, 即

由式(8) 的第一式和第二式可知:

即组合梁的净轴力(子梁C 和子梁S 的轴力和) 为常量, 设为N0, 则

由式(2) 和(9) 可得

由控制方程(8) 可得, 以wc、ws和ur为基本未知量的组合梁静力弯曲控制方程为

2 组合梁弯曲的解析解

为使控制方程的解具有一般性, 引入如下无量纲量和参数, 即

由控制方程(12) 得到组合梁静力弯曲的无量纲控制方程, 即

式(14) 的第二式和第三式相加, 可得

式中,C1为待定常数, 且

将式(15) 代入式(14), 消去Ur, 得到以Wc和Ws为基本未知量的静力弯曲控制方程, 即

式中,C2、C3和C4为待定常数, 且

对控制方程(17) 进行Laplace 变换, 可得

式中:Ci(i=5,6,7,8,9,10)为待定常数;和(s)分别是Ws(ξ)、Wc(ξ)、P(ξ) 和Q1(ξ) 的Laplace 变换. 由此可得,

式中:

为进一步进行Laplace 逆变换, 令x=s2, 考察如下的一元三次方程:

由盛金公式[30]可知,G(s) 可表示为

式中: i2=-1;

F(s)=1/G(s) 可表示为

式中:

利用式(27) 对式(20) 和(21) 进行Laplace 逆变换后, 可得控制方程(19) 的通解分别表示为

式中:F0(ξ)、Fmi(ξ)(i=1,2,3,4)、Fpi(ξ)(i=1,2,3,4,5)为已知函数;Wcp(ξ)、Wsp(ξ)、Wcq(ξ)和Wsq(ξ) 为与P(ξ) 和Q1(ξ) 有关的卷积. 限于篇幅, 这里略去其表达式.

进而可根据式(15)、(11) 和(3), 得到界面间的无量纲滑移位移Ur(ξ)、子梁C 和子梁S的无量纲轴力Tc(ξ) 和Ts(ξ) 以及无量纲弯矩mc(ξ) 和ms(ξ).

3 简支组合梁的弯曲及参数分析

为考察组合梁连接面的纵向和竖向刚度ku和kw对组合梁弯曲行为的影响, 设图3 所示简支组合梁的长为L=10 m, 且其上部子梁C 和下部子梁S 的材料和几何参数一致. 子梁C和子梁S 的弹性模量Ec=Es= 3.25×104N/mm2. 图4 所示两子梁的矩形截面梁的宽为bc=bs=3 000 mm, 梁高为hc=hs=500 mm. 设组合梁无净轴力, 即T0=0. 此时, 无量纲参数下面分析不同加载方式下, 简支组合梁在无量纲横向均布载荷Qc(ξ)=Qc0和Qs(ξ)=Qs0作用下的弯曲行为, 重点考察连接面竖向刚度kw与纵向刚度ku对组合梁变形与内力的影响.

图4 组合梁横截面的几何尺寸Fig.4 Geometric parameters of the crosssection of composite beam

对于简支梁, 相应的无量纲边界条件为

根据边界条件(31), 可求得待定常数Ci(i= 1,2,··· ,10), 从而得到均布载荷下具有界面滑移与掀起的简支单跨组合梁的弯曲解析解Ws(ξ)、Wc(ξ) 和Ur(ξ), 进而得到子梁C 和子梁S 的无量纲轴力Tc(ξ)、Ts(ξ) 和无量纲弯矩mc(ξ)、ms(ξ).

3.1 上部加载时组合梁连接界面刚度对组合梁弯曲变形的影响

为考察上部加载时, 界面无量纲纵向刚度ku和无量纲竖向刚度kw对组合梁变形及内力的影响, 设组合梁仅上部受无量纲竖向均布载荷的作用. 这里取Qc0=2 和Qs0=0.

数值计算结果表明: 当无量纲竖向刚度kw很大(kw＞103) 时, 子梁C 和子梁S 的无量纲挠度Wc、Ws以及无量纲弯矩mc、ms趋于一致. 图5 分别给出了当无量纲竖向刚度为kw=3×103时, 不同无量纲纵向刚度ku下, 子梁C 和子梁S 的无量纲挠度Wc、Ws和无量纲弯矩mc、ms、界面间无量纲滑移位移Ur, 以及无量纲轴力Tc=-Ts沿梁轴线ξ的分布.可见: 对于仅子梁C 承受均布载荷的简支单跨组合梁, 子梁C 和子梁S 的无量纲挠度Wc和Ws沿梁轴线ξ呈对称分布, 跨中挠度最大; 界面间无量纲滑移位移Ur沿梁轴线ξ呈反对称分布, 跨中滑移为0, 端部滑移位移最大; 子梁C 和子梁S 的无量纲弯矩mc、ms和无量纲轴力Tc=-Ts均沿梁轴线ξ呈对称分布, 且跨中受力最大.

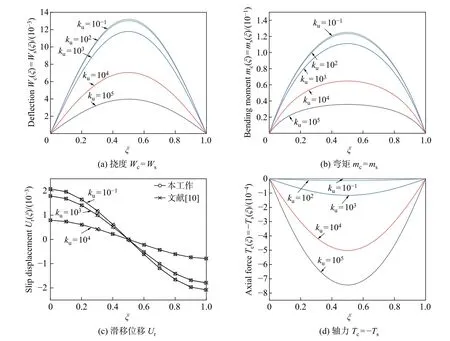
图5 当kw =3×103 时, 不同ku 下简支单跨组合梁变形及内力沿轴线ξ 的分布Fig.5 Deformation and internal forces along the axial line ξ of the simply-supported single span composite beam with different ku when kw =3×103

同时, 图5(c) 也给出了忽略界面掀起效应, 仅考虑界面滑移效应的组合梁弯曲二阶算法解析解[10]的结果. 可见, 当界面无量纲竖向刚度为kw= 3×103, 即竖向刚度很大时, 不同界面无量纲纵向刚度ku下, 考虑界面滑移与掀起效应组合梁弯曲结果, 可退化为忽略界面掀起效应, 仅考虑纵向滑移效应的部分剪力相互作用组合梁的弯曲结果[29]. 这从一个方面说明了本工作的解析解具有准确性与合理性.

图6 分别给出了不同无量纲竖向刚度kw下, 子梁C 和子梁S 的无量纲跨中挠度Wc0、Ws0和无量纲跨中弯矩mc0、ms0、无量纲端部界面滑移位移Ur0, 以及无量纲跨中轴力Tc0=-Ts0随界面无量纲纵向刚度ku的变化. 此时, 由于子梁C 和子梁S 的材料与几何性能相同, 二者位移与内力的差异仅由界面无量纲竖向刚度和无量纲纵向刚度产生. 可见: 随着无量纲纵向刚度ku的增大, 子梁C 和子梁S 的无量纲跨中挠度Wc0、Ws0和无量纲跨中弯矩mc0、ms0, 以及无量纲端部界面滑移位移Ur0均逐渐减小最后趋于稳定, 而无量纲轴力Tc0=-Ts0先逐渐增大后趋于稳定; 随着无量纲竖向刚度kw的增大, 子梁C 的无量纲跨中挠度Wc0和无量纲跨中弯矩mc0逐渐减小, 而无量纲跨中挠度Ws0和无量纲跨中弯矩ms0逐渐增大; 无量纲端部界面滑移位移Ur0和无量纲跨中轴力Tc0=-Ts0不受无量纲竖向刚度kw变化的影响, 原因是无量纲竖向弹簧引起子梁C 和子梁S 的竖向力为相反数. 因此, 竖向刚度kw变化引起的两子梁挠度之和为0. 当组合梁无量纲纵向刚度ku一定时, 有

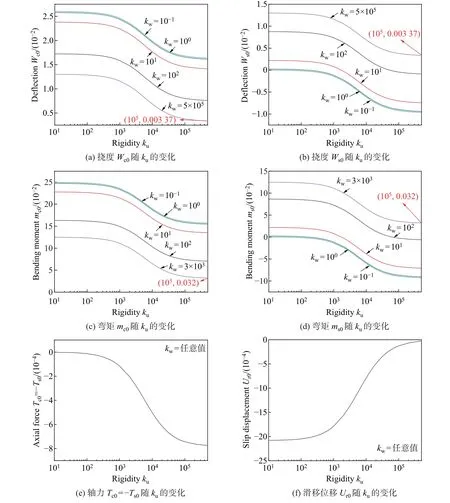
图6 不同kw 下简支单跨组合梁变形及内力随ku 的变化Fig.6 Deformation and internal forces vs. ku of the simply-supported single span composite beam with different kw

由图6 还可知: 当界面刚度为ku= 105,kw= 105时, 子梁跨中无量纲挠度为Wc0=Ws0= 3.37×10-3, 两梁跨中无量纲弯矩为mc0=ms0= 0.032, 组合梁跨中横截面正应力对Oy轴的无量纲弯矩为均布载荷Qc0= 2 下经典简支梁跨中无量纲挠度W0= 5qL3/(384EcIc) = 3.30×10-3, 跨中无量纲弯矩m0= (qL3/8EcIc) = 0.25[31]. 可见, 当连接面抗剪刚度、抗拉刚度均较大, 即ku＞105,kw＞105时, 连接面连接效应消失, 组合梁可视为一个完整梁.

3.2 不同加载方式下界面刚度对组合梁弯曲变形的影响

为探究不同加载方式时, 界面无量纲纵向刚度ku与界面无量纲竖向刚度kw对组合梁变形及内力的影响, 考察下列3 种加载方式: ①Qc0= 2,Qs0= 0; ②Qc0= 0,Qs0= 2;③Qc0=1,Qs0=1.

图7 给出了在上述加载方式下, 当ku= 10-1时, 子梁C 和子梁S 的无量纲跨中挠度Wc0和Ws0、无量纲跨中弯矩mc0和ms0等随无量纲竖向刚度kw的变化. 图8 给出了在上述加载方式下, 当kw= 10-1时, 子梁C 和子梁S 的无量纲跨中挠度Wc0和Ws0、无量纲跨中弯矩mc0和ms0等随无量纲纵向刚度ku的变化. 结果显示: 对于加载方式②, 即当组合梁仅下部受均布载荷作用时, 子梁C 与子梁S 的挠度及内力与加载方式①仅上部加载时恰好相反; 随着无量纲纵向刚度ku的不断增大, 子梁C 和子梁S 的无量纲挠度Wc0和Ws0、无量纲弯矩mc0和ms0、无量纲界面纵向滑移位移Ur均逐渐减小, 最后趋于稳定; 子梁C 和子梁S 的无量纲轴力Tc=-Ts逐渐增大, 最后趋于稳定; 随着界面无量纲竖向刚度kw的不断增大, 子梁C 的无量纲挠度Wc0和弯矩mc0逐渐增大, 最后趋于稳定; 下部子梁S 的无量纲挠度Ws0和弯矩ms0逐渐减小, 最后趋于稳定; 当kw＞103时, 两子梁的挠度Wc、Ws和弯矩mc、ms均趋于一致且不再改变, 而连接面界面的无量纲纵向滑移位移Ur、两子梁的无量纲轴力Tc=-Ts均不随无量纲竖向刚度kw的变化而变化; 当ku＞105时, 组合梁的变形及内力均趋于常值.

图7 当ku =10-1 时不同加载方式下简支单跨组合梁变形及内力沿kw 的变化Fig.7 Deformation and internal forces vs. kw of the simply-supported single span composite beam under different loading modes when ku =10-1

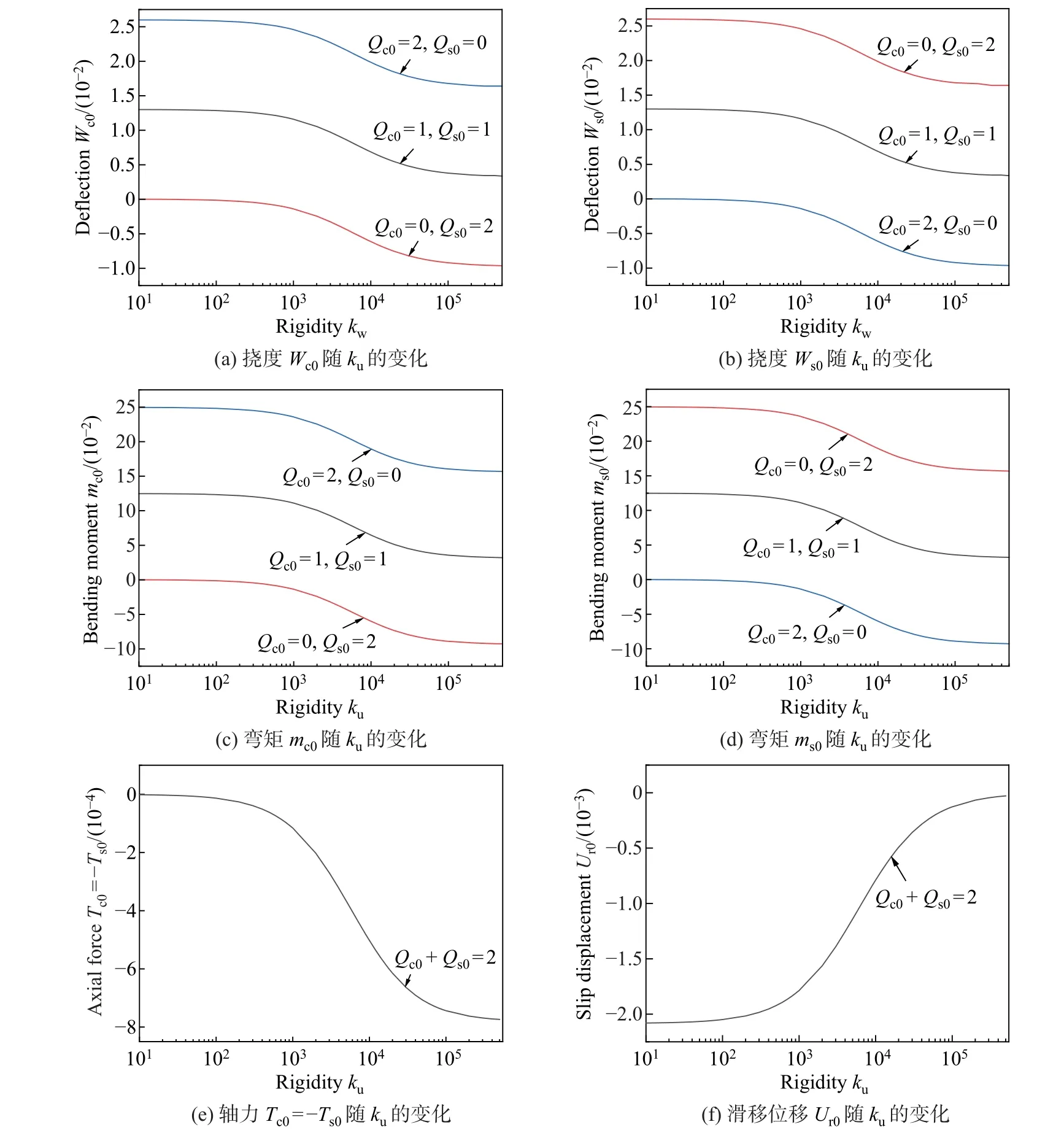
图8 当kw =10-1 时不同加载方式下简支单跨组合梁变形及内力随ku 的变化Fig.8 Deformation and internal forces vs. ku of the simply-supported single span composite beam under different loading modes when kw =10-1

当组合梁上部与下部分别承受相同载荷, 即加载方式③时, 无量纲竖向刚度kw对组合梁变形及内力均没有影响. 随着无量纲纵向刚度ku的不断增大, 子梁C 和子梁S 的无量纲挠度Wc0和Ws0、无量纲弯矩mc0和ms0、无量纲界面纵向滑移位移Ur0均逐渐减小, 最后趋于稳定. 子梁C 和子梁S 的无量纲轴力Tc=-Ts均逐渐增大, 最后趋于稳定. 由此可见: 当加载方式不同时, 子梁C 和子梁S 的无量纲挠度Wc0和Ws0、无量纲弯矩mc0和ms0的响应也不同, 但无量纲滑移位移Ur和无量纲轴力Tc=-Ts不受加载方式的影响; 随着无量纲竖向刚度kw的增大, 加载方式对组合梁变形及内力的影响逐渐减小; 而无量纲纵向刚度ku的变化无法消除加载方式对组合梁变形的影响.

4 结束语

以考虑具有连接面纵向滑移与竖向掀起的组合梁为研究对象, 在组合梁子梁满足Euler-Bernoulli 梁弯曲理论的假设下, 本工作建立了以组合梁纵向滑移和子梁竖向挠度为基本未知量的组合梁弯曲变形控制方程, 给出了简支组合梁弯曲变形的挠度、滑移位移、轴力和弯矩等的解析解. 在验证解析解正确性的基础上, 参数分析了连接面纵向滑移与竖向掀起刚度以及加载方式等对均布载荷作用下简支组合梁弯曲变形的影响, 得到如下的主要结论.

(1) 当连接面无量纲竖向刚度kw＞103时, 组合梁可等效为仅考虑界面滑移的部分剪力相互作用组合梁, 此时两子梁挠度趋于一致. 当连接面无量纲竖向刚度kw＞103, 无量纲纵向刚度ku＞105时, 组合梁等效于完全剪力相互作用的组合梁. 当连接面无量纲竖向刚度kw＜10-1, 无量纲纵向刚度ku＜101时, 该组合梁等效于不考虑界面相互作用的两个独立的梁.

(2) 对受均布载荷作用的简支组合梁, 无论采用何种加载方式, 随着连接面纵向刚度的不断增大, 组合梁的挠度、弯矩、界面滑移位移均先减小后趋于不变, 轴力先增大后趋于不变.

(3) 对于上部受均布载荷作用的简支单跨组合梁, 随着界面竖向刚度的不断增大, 上梁竖向挠度、弯矩先减小后趋于不变, 下梁竖向挠度、弯矩先增大后趋于不变, 界面滑移位移、轴力与界面竖向刚度的取值无关. 对于下部受均布载荷作用的简支单跨组合梁, 随着界面竖向刚度的不断增大, 上梁竖向挠度、弯矩先增大后趋于不变, 下梁竖向挠度、弯矩先减小后趋于不变, 界面滑移位移、轴力与界面竖向刚度的取值无关. 对于上梁与下梁所受载荷一致的组合梁,界面竖向刚度对组合梁弯曲变形没有影响.

(4) 当载荷一致, 加载方式不同时, 组合梁竖向挠度、弯矩也会随之改变, 但界面滑移位移、轴力不受加载方式的影响. 界面竖向刚度的增大可以消除加载方式对组合梁弯曲变形的影响.