欧拉公式的一种函数证明

贵州省黔南布依族苗族自治州都匀第一中学(558000) 罗凤虎

1 欧拉公式的证明

欧拉公式的具体内容是eix= cosx+i sinx(x∈R),首先就这个公式给出两种证明方法,这两种方法主要涉及高中导函数知识,比较利于高中学生的理解,具体如下：

1.1 第一个证明方法

1.2 第二个证明方法

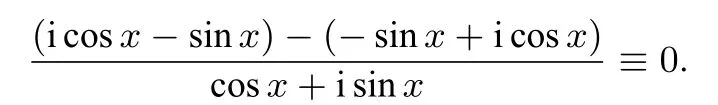
所以函数f(x)=ix-ln(cosx+i sinx)(x∈R)是常数函数, 又f(0) = 0·i - ln(cos 0+i sin 0) = 0 - ln 1 = 0,所以f(x)≡f(0) = 0, 即ix- ln(cosx+i sinx) = 0即ix= ln(cosx+i sinx), 两边取以e 为底的指数, 得eix=cosx+i sinx. 原式得证.

1.3 公式证明的思路分析

第一个证明方法分析: 因为e-ixeix= e0= 1, 所以eix/= 0, 不妨构造函数(cosx+i sinx)(x∈R),只需证明f(x)≡1 为常数函数,即证f(x)的导函数恒等于0,且f(0)=1.

第二个证明方法分析: 对eix= cosx+i sinx(x∈R),两边取自然对数得ix= ln(cosx+i sinx), 不妨构造函数f(x) = ix-ln(cosx+i sinx)(x∈R), 只需证明f(x)≡0为常数函数即可,即证f(x)的导函数恒等于0,且f(0)=0.

1.4 公式应用

以一个实例来说明公式的应用,例子如下:

计算ii=____.[1]

解: 在欧拉公式eix= cosx+i·sinx中, 令有结果的值是实数.

以上证明和实例表明, 可以用高中学生可理解的方式,在形式上证明了欧拉公式,给学生提供新的视角,提高学生对数学学习的兴趣和好奇心.