由学生提问引发的深度学习——以“多边形的外角和”教学为例

广东省广州市华侨外国语学校 (510095) 陈文阳 广东实验中学越秀学校(510095) 胡燕芬

美国著名学者布鲁巴克指出,最精湛的教学艺术,遵循的最高准则就是让学生自己提出问题[1]. 因为学生提出有价值的数学问题,是最精彩的课堂生成,是最宝贵的学习资源,能引发学生的深度学习. 教学中,借助学生提出的具有群体探究价值的数学问题, 让学生广泛地参与到问题解决之中,通过群体思考与探索获得认知发展,能实现学生的深度学习.现以人教版教材八年级上册第十一章“三角形”中“多边形的外角和”教学为例,呈现与分析笔者引导学生发现和提出数学问题,并在分析和解决问题中发生深度学习的课堂实践.

1 案例呈现

这是一节新授课,教学内容是多边形的外角和. 课堂伊始,学生结合教师设计的问题,精读教材,理解学习内容,记录疑问之处或联想到的问题. 接着,在师生互动与交流中回答教师所提出的问题,学生习得“多边形的外角和是360°”.随后,教师让学生说出自己的问题. 其中,甲同学问:“如果多边形的边数越来越多,多边形就慢慢变成了一个圆,它的外角也就慢慢变小为0°,那么它的外角和还是360°吗? ”

甲同学的问题引起班上学生的热烈讨论. 有学生说:“多边形的边数很多时,它依然是一个多边形,不会变成圆. ”也有学生说:“多边形的边数无穷多时就变成圆,那么每个外角就变小为0°,所以它的外角和为零. ”还有学生说:“就算是多边形变成了圆,若沿圆走一周,刚好转了360°,所以它的外角和还是360°.”……

看到学生意见不一, 教师通过提问指导学生分析问题,大致过程如下.

师: 若多边形的边数趋于无穷大时,每一个外角的大小都趋于0°,这个趋于0°是等于0°吗?

生: 不等于.

师: 无数个不等于0°的外角相加有可能等于0°吗?

生: 不可能.

师: 所以当多边形的边数趋于无穷大时,它不会变成圆,其外角和仍为360°.

此时,乙同学问:“当边数足够大的时候,我们肉眼看到的多边形就接近圆了. 如果把多边形换成了圆,那么沿圆周走一周,所转的各个角的和真的是360°吗? ”

不一会,丙同学问:“沿圆走时,转过的角度应该怎么表示呢? ”

接着,丁同学问:“绕圆心转一周可得到一个周角360°,但沿圆走时转过的角的顶点并不在圆心呀,怎么能说明所转的各个角的和是360°呢? ”

学生们陷入了沉思. 教师再次引导学生分析问题,大致过程如下.

师: 如果能找到沿圆周从一个位置走到另一个位置时,所转过的角度与顶点在圆心的角(此时教师补充了圆心角的概念)的关系,将所有转过的角度之和转化为一周的圆心角,那么我们就能说明沿圆周走一周,所转的各个角的和是360°.

不妨规定,在圆上某一点的前进方向与这一点所在的半径互相垂直. 如图1, 在点A, 点B的前进方向分别是射线AM(AM⊥OA),射线BN(BN⊥OB)的方向. 如果从点A处出发,沿着圆O走到点B处,那么所转过的角可以用哪个角来表示呢?

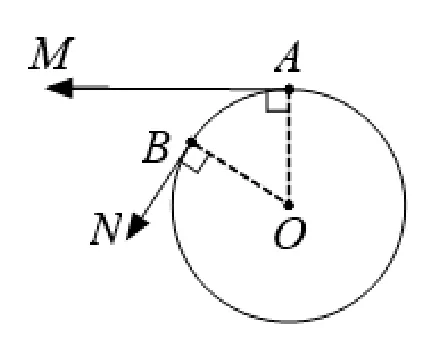
图1

生: 反向延长BN, 交AM于点D, 则所转过的角是∠MDN. (如图2)

图2

师: 图中哪个角与∠MDN相等?

生: ∠AOB.

师: 如何说明?

生: 在四边形AOBD中,∠OAD+∠OBD= 180°,则∠AOB与∠ADB互补. 又因为∠MDN与∠ADB互补,所以∠AOB=∠MDN.

师: 很好! 还有别的说明方法吗?

生: 延长OB交AM于点E,可知∠AOB,∠MDN都与∠AEO互余,则∠AOB=∠MDN. (如图3)

图3

师: 非常好! 如图4,若沿圆O从点B走到点C,则所转过的角等于哪个角?

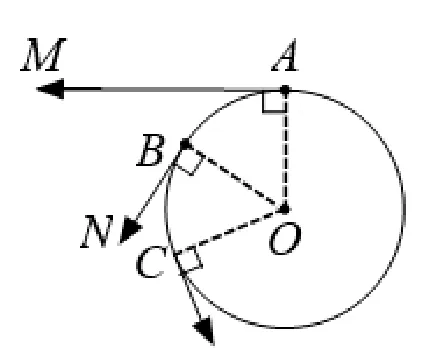
图4

生: ∠BOC.

师: 若沿圆O从点A走到点C,所转过的角之和等于哪个角?

生: ∠AOC.

师: 若沿圆O从点A走一周回到点A,所转过的角之和等于哪个角?

生: 以点O为顶点的周角.

师: 由上面的探究,你能得到什么结论?

生: 沿圆周走一周,所转的各个角的和是360°.

至此,师生一起解决了课堂上学生提出的问题.

2 案例分析

深度学习是指在理解学习的基础上,学习者能够批判性地学习新的思想和事实, 并将它们融入原有的认知结构中,能够在众多思想间进行联系,并能够将已有的知识迁移到新的情境中,作出决策和解决问题的学习[2]. 上述案例是由学生提问引发的深度学习过程,主要体现在以下四个方面.

2.1 学生能批判性理解学习

批判性理解学习包含批判性和理解性两个方面. 批判性学习强调学生的独立思考能力,理解性学习强调学生参与体验问题解决过程,得出新结论并能用新结论解决问题. 案例中,学生先根据教师设计的问题自主阅读教材,产生认知冲突、发现问题,为后续提出问题和合作学习奠定了基础,充分体现学生的独立思考与质疑精神. 比如,甲同学通过读、研、思, 产生疑惑, 提出关于“多边形的边数趋于无穷时的外角和”的问题. 师生通过交流,解决甲同学的问题之后,乙同学开始反思,从而提出关于“沿圆周走一周,所转的各个角的和是否为360°? ”的新问题. 这促使同学们进一步思考,提出新假设“沿圆走时,转过的角度可以转化为圆心角”,进而在新结论的基础上解决了新问题. 深度学习意味着理解与批判,需要学生对知识持敢于质疑、敢于批判的态度,能发现和提出问题,更能进一步分析和解决问题.

2.2 学生能迁移与应用知识

迁移与应用是深度学习的特征之一, 只有学生能联系原有认知结构中的知识、学会应用数学知识解决新问题, 才能拓宽知识的广度和提升知识的深度. 案例中, 学生在“多边形外角和是360°”的基础上,联想并讨论了“圆的外角和”, 构建了新的认知结构和环境. 通过阅读教材,学生习得用图形方法验证“多边形内角和为360°”,即从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向,在行程中所转的各个角的和,就是多边形的外角和(如图5). 课堂上,学生能类比教材的方法,尝试用图形来理解“沿圆周走一周,所转的各个角的和”的问题,这就是在迁移与应用已有知识. 在探究“沿圆走时, 转过的角度等于圆心角”时,学生借助上一节课学习的“四边形的内角和为360°”推导出对角互补(图2 中∠AOB与∠ADB互补),从而说明“转过的角等于圆心角”,这是学生深刻理解和灵活应用已学知识的具体体现.

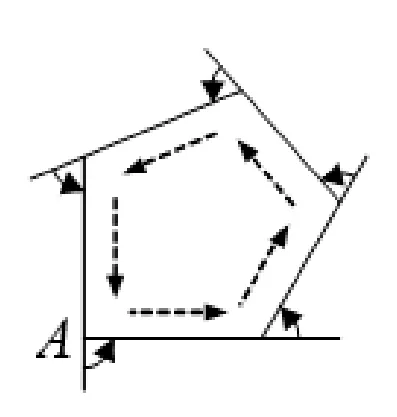
图5

2.3 学生的问题解决有突破

提升学生解决问题的能力是深度学习的目标之一,而提出问题能帮助学生成为更好的解决问题者. 波利亚认为,对初始问题连续的再阐述是在问题解决中提出问题的基本形式[3]. 案例中,讨论甲同学的问题时,学生针对多边形边数越来越多的情形,能从“它会不会变成圆? ”“它的外角是不是变小为0°? ”“它的外角和是否还是360°? ”等不同角度去分析问题. 教师的“趋于0 是否就等于0? ”等连续提问,为学生解决甲同学的问题搭起“脚手架”. 分析乙同学的问题时,丙、丁同学的提问是将原问题分解为“怎么表示在圆上走时转过的角度? ”和“怎么把转过的角转化为其对应的圆心角? ”,使解决问题的思路逐渐清晰,突破了问题解决的瓶颈.

提出问题是解决问题的有效手段,问题的重建则是提出问题的技术操作. 案例中,不管学生在问题解决之前、之中或者之后提出新的问题, 都是在对已有问题进行重建或加工,都能揭示学生的认知思维过程,有助于学生深度理解数学问题的本质,提升学生解决数学问题的能力.

2.4 学生的数学思维有创新

问题是一种蕴涵创造力的数学发现,学生自主精读教材并提出问题是一种通过独立思考发现新知识的“再创造”. 深度学习是学生经历实践创新的过程,而学生的创新往往始于问题的提出. 案例中,甲同学的问题,看似简单实属不易,因为在没有教师提示的情况下,能由方(多边形)到圆(圆形)迁移性地思考问题,是学生数学思维的重大转变和创新. 创造性思维的过程中,新假设的产生需要灵感,而灵感萌生的基础是有意注意. 学生并没有听过“圆的外角和”的说法,但能从多边形外角和的探究过程中留意到边数的变化规律,考虑到边数为极限的情形,于是联想到探究“圆的外角和”,这是学生创新思维的一次升华.

真正的创造力并不能还原为自由组合和联想,而在于能够提出新问题,或者改变旧问题,改变既有思路,重新建立规则和方法[4]. 案例中,乙同学的提问就是甲同学问题的衍生,而丙、丁同学的提问则是从新的方向去分解乙学生的问题,这是学生思维朝高阶发展的表现. 学生能提出“新问题”或“从新的角度去看原有问题”,这反映出学生创造性的想象力和意味着深度学习的发生.

3 教学反思

深度学习是指在教师引领下,学生围绕着具有挑战性的学习主题, 全身心积极参与、体验成功、获得发展的有意义的学习过程[5],其本质是以“问题”为驱动,促进学生发现、提出、分析和解决问题的一种具有探索性和创造性的过程. 案例中,甲、乙同学的提问逐步启发学生去探究一个未曾深思的问题: 沿圆走一周,转过的角度之和是多少? 虽然不少学生凭感觉认为是360°,但又有几个能说明其中的道理呢? 面向问题解决的数学学习就是要使学生的思维从感性向理性转化,达成直觉思维和分析思维的高度统一,这也是深度学习的重要意义. 换而言之,“问题”是深度学习的重要载体,是深度学习的出发点. 但目前学生提出问题的能力还较为薄弱,如何提高学生的提问能力, 以更好地促进学生的深度学习,还有待我们进一步研究.