基于深度学习下的概念课实践*——以函数的零点与方程的解为例

广东省兴宁市第一中学(514500) 赖海波

深度学习是机器学习的一种,是实现人工智能的必经路径,是一个源于人工神经网络的研究的概念. 课堂教学中,借助合理的深度学习,全面构建数学学习共同体,有效提升数学知识、数学思想方法和数学能力等,是提升课堂教学效果的一个重要途径. 特别在概念教学过程中,深度学习显得更为重要.

1 深度学习的必要性

1.1 探究概念的来龙去脉

借助深度学习,合理挖掘概念的根源,培养学生对知识探究的浓厚兴趣和探究欲望. 通过自身对数学概念的探究,加强内驱力,进而理清概念发展的脉络,构建与之相关的概念体系与数学知识体系,对知识的学习与体系的构建很有帮助.

1.2 拓展知识的深层理解

借助深度学习,在表层概念的基础上,通过对概念等知识的批判性的理解与接收,合理内化,融入自身已有的知识系统中去,合理实现与已有认知与知识的连接与联系,从而加大加深对知识的理解与应用,为知识的迁移与学习拓展更加广阔的空间.

1.3 注重知识的交汇融合

借助深度学习,对相关概念的学习基础上,进一步加深与其他知识的联系与关联,从而构建起不同知识之间的交汇与融合,开拓知识的枝蔓,强化新知识内化以及与原有知识之间的联系,形成一个更加综合的新模式.

1.4 养成良好的核心素养

借助深度学习,在概念等相关知识理解与掌握的基础上,融入数据分析、数学抽象、逻辑推理、数学建模、直观想象以及数学运算等核心素养,更能批判性地学习新思想和新知识,并巧妙融入已有的认知与知识体系中去,形成对知识的更深层次的理解与迁移,培养学生的思想方法、创新意识与数学能力.

2 深度学习的课堂实践

2.1 导学聚焦

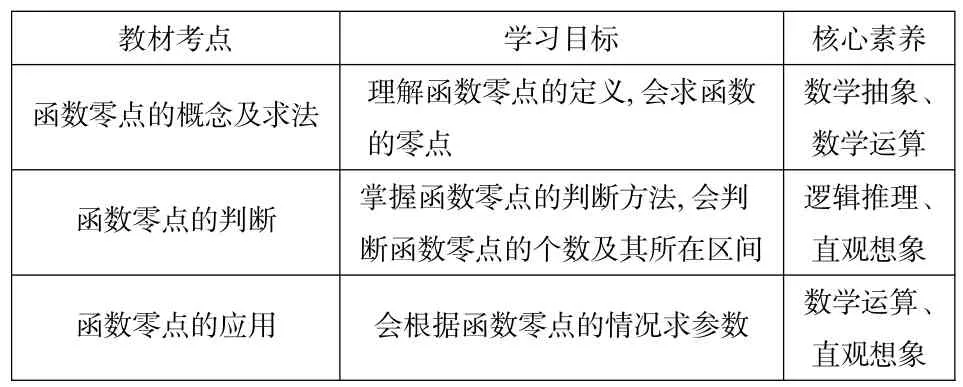
教材考点学习目标核心素养函数零点的概念及求法理解函数零点的定义,会求函数的零点数学抽象、数学运算函数零点的判断掌握函数零点的判断方法,会判断函数零点的个数及其所在区间逻辑推理、直观想象函数零点的应用会根据函数零点的情况求参数数学运算、直观想象

理清学习目标与考点,对应相应的核心素养,为课堂的概念教学确立明确的目标与理念,围绕这些基本目标来学习.

2.2 问题导学

预习人教A 版2019 必修第一册P142-P144,并思考以下问题:

(1)函数零点的概念是什么?

(2)如何判断函数的零点?

(3)方程的根、函数的图象与x轴的交点、函数的零点三者之间的联系是什么?

强调自主学习,也为深度学习提供条件与过渡. 在学生自主学习的基础上,通过课堂的概念教学加以深入,全面提升深度学习的效果.

2.3 概念形成

(1)概念: 对于一般函数f(x),我们把使f(x) = 0 的实数x叫做函数y=f(x)的零点.

(2)方程的根、函数的图象与x轴的交点、函数的零点三者之间的联系

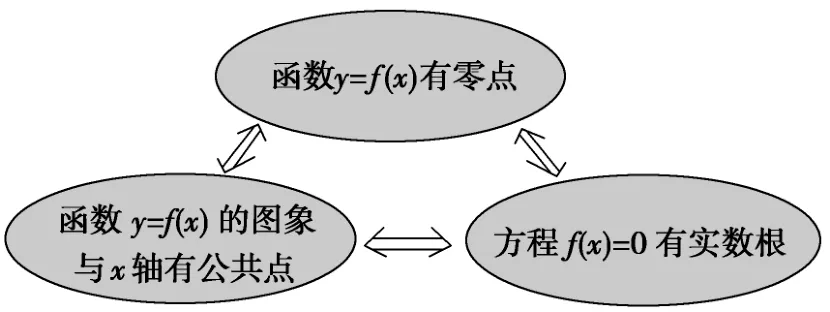
提出问题: (1)函数的零点是点吗?

提示: 函数的零点不是一个点,而是一个实数,当自变量取该值时,其函数值等于零.

提出问题: (2)函数的零点个数、函数的图象与x轴的交点个数、方程f(x)=0 根的个数有什么关系?

提示: 相等.

提出问题: (3)结合所学的基本初等函数(如一次函数、二次函数、指数函数、对数函数),思考是否所有的函数都有零点? 并说明理由.

提示: 不一定. 因为函数的零点就是方程的根,但不是所有的方程都有根,所以说不是所有的函数都有零点. 如: 指数函数,其图象都在x轴的上方,与x轴没有交点,故指数函数没有零点.

不停留在概念的表层,通过提出问题,反馈信息,深度理解并掌握相关概念的深层次的内涵与实质,也是深度学习的一个层面.

2.4 定理剖析

函数零点存在定理:

条件 (1)函数y =f(x)在区间[a,b]上的图象是一条连续不断的曲线.(2)f(a)·f(b)＜0.结论 函数y =f(x)在区间(a,b)内至少有一个零点,即存在c ∈(a,b),使得f(c)=0,这个c 也就是方程f(x)=0 的根.

提出问题: (1)函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,f(a)·f(b)＜0 时,能否判断函数在区间(a,b)上的零点个数?

提示: 不能.

提出问题: (2)在零点存在定理中,若f(a)·f(b)＜0,则函数f(x)在(a,b)内存在零点. 则满足什么条件时f(x)在(a,b)上有唯一零点?

提示:f(x)在(a,b)内为单调函数.

提出问题: (3)函数y=f(x)在区间(a,b)上有零点,是不是一定有f(a)·f(b)＜0?

提示: 不一定,如f(x) =x2在区间(-1,1)上有零点0,但是f(-1)·f(1)=1×1=1＞0.

加深对定理的理解与掌握,全方位、多层面加以理解与掌握,也为零点的应用这一深度学习目标提供依据.

2.5 零点应用

2.5.1 零点的确定

A. {1} B. {-1}

C. {-1,1} D. {-1,0,1}

解析: 当x≤0 时,f(x) =x+1 = 0⇒x= -1; 当x＞0 时,f(x) = log2x= 0⇒x= 1,所以函数f(x)的所有零点构成的集合为{-1,1},故选择答案: C.

规律方法总结: 求函数y=f(x)的零点通常有两种方法: 一是令f(x) = 0,根据解方程f(x) = 0 的根求得函数的零点;二是画出函数y=f(x)的图象,图象与x轴的交点的横坐标即为函数的零点.

2.5.2 零点的区间

A. (1,2) B. (2,3)

C. (3,4) D. (e,+∞)

解析: 因为f(1)=-2＜0,f(2)=ln 2-1＜0,所以在(1,2)内f(x)无零点,选项A 错;又所以f(2)·f(3)＜0,所以f(x)在(2,3)内有零点,故选择答案: B.

规律方法总结: 判断函数零点所在区间的3 个步骤:①代入: 将区间端点值代入函数解析式求出相应的函数值;②判断: 把所得的函数值相乘,并进行符号判断; ③结论: 若符号为正且函数在该区间内是单调函数,则在该区间内无零点,若符号为负且函数连续,则在该区间内至少有一个零点.

2.5.3 零点的个数

例3. 函数f(x) = lnx+x2-3 的零点的个数为____个.

解析: 因为f(1) = -2,f(2) = ln 2 + 1＞0, 所以f(1)·f(2)＜0, 又f(x) = lnx+x2- 3 的图象在(1,2)上是不间断的, 所以f(x) 在(1,2) 上必有零点, 又f(x) 在(0,+∞)上是单调递增的,所以零点只有一个,故填答案: 1.

规律方法总结: 判断函数存在零点的2 种方法: ①方程法: 若方程f(x) = 0 的解可求或能判断解的个数,可通过方程的解来判断函数是否存在零点或判定零点的个数; ②图象法: 由f(x)=g(x)-h(x)=0,得g(x)=h(x),在同一平面直角坐标系内作出y1=g(x)和y2=h(x)的图象,根据两个图象交点的个数来判定函数零点的个数.

2.5.4 交点的确定

例4. 函数f(x)=xlg(x+2)-1 的图象与x轴的交点个数有____个.

解析: 令x·lg(x+2)-1=0,所以画出函数y= lg(x+ 2)与函数在区间(-2,+∞) 上的图象, 如图所示,那么相应的函数图象有2 个交点,故填答案: 2.

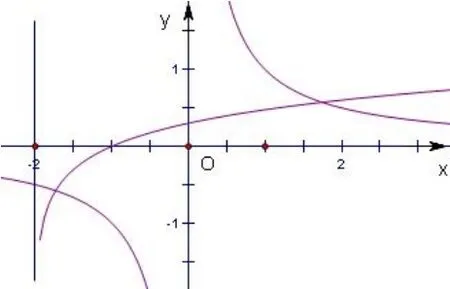
规律方法总结: 这类问题一般不易解方程求解,而是根据图象与性质直接判断,尤其是那些方程两端对应的函数类型不同的方程,多以数形结合方法求解.

2.5.5 参数的求解

例5. 若函数f(x)=mx2-2x+3 只有一个零点,求实数m的取值范围.

解析: (1)当m= 0 时,函数f(x) = -2x+3 是一次函数,令f(x)=0 得函数f(x)=mx2-2x+3 只有一个零点,符合题意;(2)当m/=0 时,函数f(x)=mx2-2x+3是二次函数,要使函数只有一个零点,应使方程f(x) = 0 只有一个实数根,因此Δ=(-2)2-4×m×3=0,得

综上分析,实数m的取值范围是m=0 或

规律方法总结: 已知函数有零点(方程有根)求参数取值范围的方法: ①直接法: 直接根据题设条件构建关于参数的不等式,通过解不等式确定参数的取值范围; ②分离参数法:先将参数分离,然后转化成求函数值域问题加以解决; ③数形结合法: 先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解[1].

借助零点的应用,多视角多层面展开,有效应用并验证函数的零点概念与函数零点存在定理,也为具体问题的分析与求解提供条件,并进一步总结规律方法,这才是深度学习的目的之一.

3 深度学习的教学启示

3.1 把握学情,合理设计

数学深度学习具有本源性、联系性、整合性和建构性等特征,在实际数学概念的教学过程中,要充分挖掘数学概念及其对应的课程资源,调动学生的主体性并合理把握学生的实际情况,巧妙设计深度学习的课堂教学实践过程,兼顾数学课程和学生学情之间合理链接,有机衔接,自然过渡,而不是构建概念学习的“空中楼阁”与抽象思维,落到实处,才能真正推进数学深度学习,形成有效深度学习[2].

3.2 缓慢过程,逐步提升

借助数学概念的教学,结合解题研究,从数学概念的浅显理解走向深刻掌握,并借助实例应用,形成概念学习的逐渐上升与螺旋前进的过程,是数学教学与解题研究中追求的一种理想状态,需要师生不断加以反馈与加深,才能形成良好的深度学习,培养良好的数学习惯,提升数学能力.

学生借助深度学习,进一步完善数学的知识体系,形成良好的认知结构,逐步实现数学学习从“学会”到“会学”,并不断过渡到“会用”的数学学习新境界,形成数学能力,提升数学品质,发展核心素养[2].