建构知识联系 促进认知深化

苏国东

【摘 要】  “平行四边形”章节概念较多，学生容易混淆，出现多用、少用或错用条件等现象，理清各类四边形的转化关系是正确运用知识的前提.通过几何画板动态演示建立联系、知识结构图呈现条件梳理联系、开展拼图活动应用联系、设计添条件开放性问题深化联系，是四边形转化关系教学的有效策略.

【关键词】  平行四边形；转化关系；几何画板

“四边形的转化关系”是人教版八年级下册第十八章“平行四边形”的重要教学内容.在本章的教学中，既要让学生理解平行四边形、矩形、菱形和正方形的定义、判定和性质，更要帮助学生掌握各类四边形相互之间的联系与转化，灵活地应用于实际问题中.

由于本章涉及的各类四边形概念相互重叠交错，图形之间存在紧密联系，学生容易产生混淆，在应用知识时可能会出现多用、少用或错用条件等现象，因此，理清各类四边形之间的共性、特征以及转化关系尤为重要.根据笔者的实践探索，采用几何画板进行动态演示、使用知识结构图呈现概念条件、开展拼图活动以及设计添条件的开放性问题等方式，有助于建构各类四边形之间的知识联系，促进学生对四边形转化关系的认知深化.

1 动态演示，建立联系

在本章关于各类四边形定义的教学中，教师应有意识地利用几何画板等技术工具制作图形，动态演示图形的变化过程，以此形成平行四边形、矩形、菱形的定义.在讲授正方形的定义时，教师可以再次利用几何画板回顾这一演变过程，将各类四边形的相关知识进行串联和重组.

在实际教学中，教师可以使用几何画板创建两个平行四边形，并邀请两名学生上台进行操作，分别调整一个内角的大小和一条边的长度，将平行四边形的角或边特殊化.教师结合图形的变化，依次呈现出矩形和菱形的定义，以巩固学生对概念的理解.

随后，教师提出一个探究性问题：如果在平行四边形的角特殊化的基础上再对边进行特殊化，会形成什么图形？如果在边特殊化的基础上再对角进行特殊化，又会形成什么图形？两名学生继续在几何画板课件上进行操作，发现最终都能变成一个正方形，此时教师再呈现出正方形的定义.通过这个探究过程，学生可以直观地了解从平行四边形到正方形的转化路径，从感性到理性地对各类四边形之间的联系有了整体的认识.

2 结构图示，梳理联系

在学生对各类四边形之间的转化关系有了直观了解后，教师可以借助知识结构图来帮助学生进一步梳理和巩固知识.数学知识结构图能以简明扼要的形式呈现主要概念和条件关系，是帮助学生正确辨析概念、结构化整合知识的有效途径.

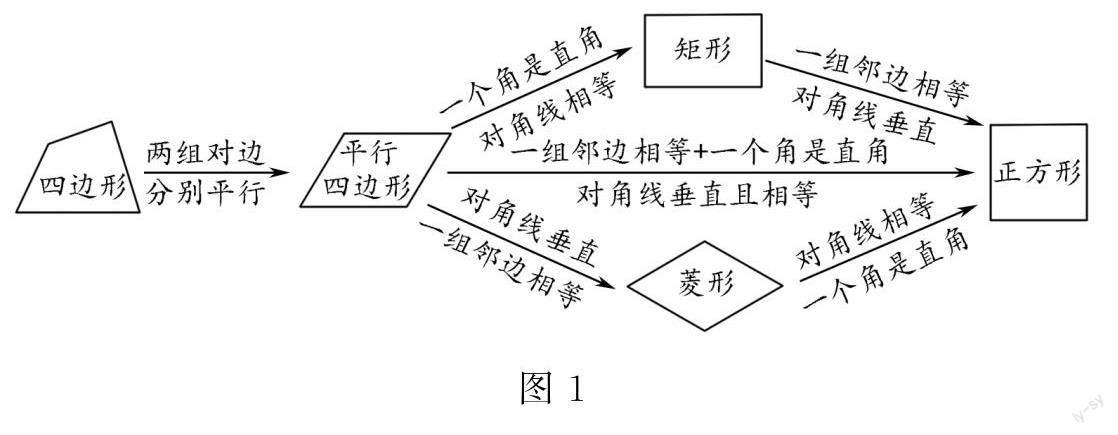
将各类四边形用近似图案表示，并用有向箭头线连接起来，连线上标注前后两个图形之间的转化条件，即形成了如图1所示的知识结构图.

在实际教学中，教师可以通过希沃白板将这些图形逐个呈现，再邀请学生上台填写连线上的标注，这样既理清了各类四边形的定义，又能让四边形的判定方法得到了完善和拓展.例如，从平行四边形变成矩形或菱形，再变成正方形的添条件方法可知，从平行四边形变成正方形可以添加一个角是直角且一组邻边相等的条件.另外，从对角线的角度考虑，通过添加对角线相等或对角线垂直的条件，同样能推导出各类四边形之间的转化关系.

在此基础上，教师可以设计一系列判定图形形状的问题，让学生能够学以致用，正确辨析图形之间的关系.

3 拼图活动，应用联系

平行四边形沿着一条对角线剪开可以得到两个全等三角形，反过来，用两个全等三角形可以拼成一个平行四边形.在实际教学中，教师可以引导学生尝试利用不同形状的全等三角形纸片拼接成平行四边形，深入理解四边形的转化关系.

學生发现通过将其中一个三角形旋转180 ° 后，可以沿着对应边拼接成一个平行四边形，而且有三种不同的拼接方法.教师请学生代表上台展示拼法，并引导其他学生以其中一种为例（如图2），应用定义和不同的判定方法来证明其为平行四边形.

随后，教师引导学生进一步探究，若要使平行四边形变为其他特殊的四边形，那么对这两个三角形的形状有何特殊要求？学生通过观察、联想和尝试操作，可以得到以下结论：

（1）因为平行四边形添加一个直角可以得到矩形，所以可令∠A=90 ° ，即用两个全等的直角三角形沿着斜边拼接可以得到一个矩形.

（2）因为平行四边形添加一组邻边相等可以得到菱形，所以可令AB=AD，即用两个全等的等腰三角形沿着底边拼接可以得到一个菱形.

（3）因为平行四边形添加一组邻边相等和一个直角可以得到正方形，所以可令AB=AD且∠A=90 ° ，即用两个全等的等腰直角三角形沿着底边拼接可以得到一个正方形.

这个拼图活动的设计以真实情境为出发点，将实际问题转化为数学问题，并建立起相应的数学模型.有助于学生更熟练地运用各类四边形的判定定理，感悟各类四边形的内在联系，加深对四边形转化关系的理解，还能培养学生发现问题、分析问题和解决问题的能力.

4 开放设问，深化联系

开放性问题是指题目提供的条件不完备，需要在求解过程中不断充实和增添条件，解题方法和结论也具有多样性和开放性的综合性问题.教师在设计开放性问题时，应给予学生充分的时间和空间进行观察、探究和扩展，引导学生发散思维，从不同的角度思考问题，形成不同的解题思路，在解决问题的过程中深化认识，强化技能，提升数学解题能力、思维品质和创新意识.

在实际教学中，教师可以设计四边形添条件问题，例如以下的问题1和2，以进一步深化学生对各类四边形的定义、判定和性质的理解，使学生能够熟练地将各类四边形的转化关系应用到实际问题中.

问题1：   如图3，在△ABC中，点D是AC的中点，四边形ABED是平行四边形，分别给△ABC添加什么条件时，四边形BECD可以变成矩形、正方形？

问题2：  如图4，点E，F，G，H是四边形ABCD四边的中点，分别给四边形ABCD添加什么条件时，四边形EFGH可以变成矩形、菱形、正方形？“请说明理由。”

当学生提出不同的增添条件时，教师还可以借助几何画板等技术工具，通过拖动图形顶点让其发生相应的变化，帮助学生完善四边形的关系架构，培养学生的动态思维能力，同时渗透运动变化的思想.

通过综合运用上述教学策略和方法，能够有效地帮助学生建构知识联系，促进他们对四边形转化关系的认知深化.学生通过实践操作、概念澄清和问题解决，能够更好地理解和应用概念，进一步了解一般与特殊的关系；通过思考和探索不同情况下四边形的转化关系，能够更好地感悟具有传递性的数学逻辑， 培养几何直观和数学推理能力.

【本文系广州市教学成果培育项目“智能教学软件促进初中数学教与学改革的研究和实施”（项目编号：2020122966）的研究成果．】