基于刘徽“割圆术”的向心加速度推导

李都 姜付锦 李弼

摘   要：圆周运动向心加速度表达式的推导是高中物理教学中的重点和难点。从台球运动中受到启发，基于刘徽“割圆术”来推导向心加速度表达式。引导学生通过逐渐增加圆内接正多边形边数的折线运动逐渐逼近圆周运动，依此来推导向心加速度，开阔学生视野，培养学生核心素养。

关键词：向心加速度；刘徽“割圆术”；核心素养

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）8-0062-3

向心加速度是高中物理中一个非常重要的概念，是后面很多知识的基础。行星绕中心天体的运动规律的研究，科学仪器如质谱仪、回旋加速器和离心机的构造，都需要理解圆周运动的向心加速度。为什么做匀速圆周运动的物体速度大小不变而方向改变时会存在加速度？为什么加速度方向指向圆心？加速度大小与轨道半径和速度之间的关系如何？回答这些问题，需要深刻理解向心加速度表达式的推导过程。

教材中向心加速度的推导，用了速度矢量运算法则、小角度的三角函数、极限思想等，但缺少必要的从直线运动到曲线运动的过渡［１－２］。这种推导对学生而言，理论性较强，数学知识要求较高，学生普遍感到很难理解，导致学生在学习“向心加速度”时有畏难情绪，甚至对这种推导的正确性产生怀疑［３］。大多数学生最后只是被动地记住了推导的结论，没有真正达到培养学生核心素养的目标。

本文基于刘徽“割圆术”来研究圆周运动［4］。其基本思想是通过等分圆周，构造圆内接正多边形的折线运动，在逐渐增加圆内接正多边形边数的基础上，用圆内接正多边形的折线运动逐渐逼近圆周运动，以此来求解圆周运动的规律。

１    学生动手实验，体验圆周运动中的力

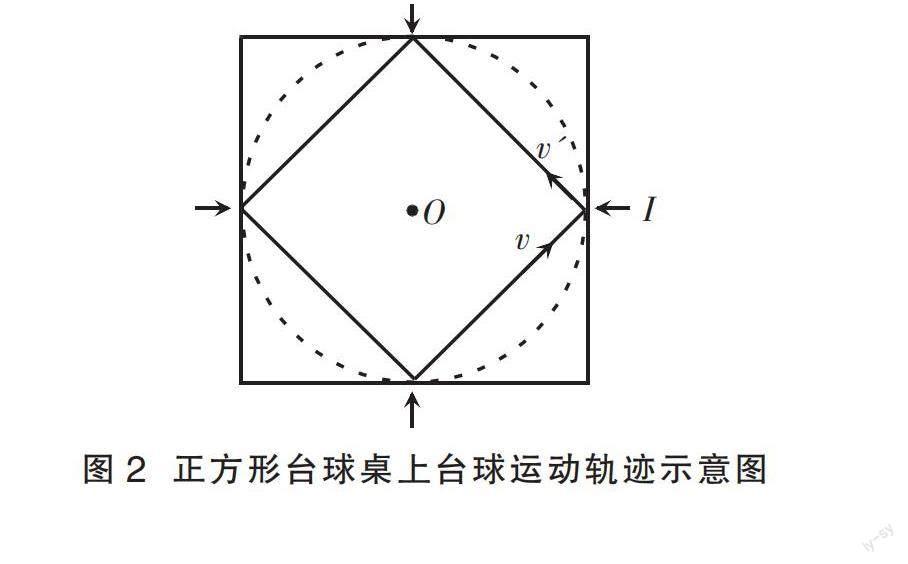
图１为正方形台球桌的实物照片。让一组学生将台球从正方形台球桌任意一边的中点击向相邻边的中点，台球在台球桌上的运动轨迹如图２所示。台球在没有与台球桌发生碰撞时，不考虑阻力，由于惯性，它只能做匀速直线运动。通过这个有趣的实验，学生可以体验到正是由于台球与台球桌的碰撞导致台球偏离原来的直线运动。每隔一段时间会有一系列同样强烈的撞击，台球会沿着环形折线运动。台球与台球桌之间发生碰撞的力为弹力，而弹力的方向与台球桌的边沿垂直，即指向环形折线外接圆的圆心。如果条件允许还可以用正六边形或者圆形台球桌做这个实验。

２    理想实验，推导向心加速度表达式

２．１    理想正六边形台球桌，构造台球轨迹

正六边形台球桌如图3所示。使台球从正六边形台球桌的某一边的中点沿与台球桌成３０°的方向以速度ｖ射出（图4），在理想情况下不计所有摩擦阻力，不计台球与台球桌碰撞过程中的能量损失。根据牛顿第一定律，在没有外部影响的情况下，在两次碰撞之间台球将保持匀速直线运动状态。

定义一个标准碰撞：一旦台球到达台球桌的边界，台球桌给它一个冲量Ｉ（箭头表示），台球偏向另一侧继续沿直线运动，直到此直线运动再次到达台球桌的边界，台球桌再次给它一个冲量，完成一次标准碰撞过程。经过若干标准碰撞，形成一个闭合路径。

在此可以设计几个问题让学生讨论回答：

（１）需要与台球桌侧面撞击多少次才能使台球形成一个完整的闭合路径？台球的轨迹是什么形状？（６次，台球的轨迹是正六边形）

（２）台球桌给台球的撞击力方向？（台球桌对台球的撞击力为弹力，方向垂直于台球桌边沿，即指向台球桌内切圆的圆心）。

２．２    量化平均加速度

在图4基础上作出一个标准的碰撞过程，如图５所示，台球的平均加速度为

图５中，在一个标准碰撞中，台球平行于台球桌边缘的速度不变，垂直于台球桌边缘的速度方向发生变化，可得速度变化量为

Δv=2v⊥=2vsin30°（2）

完成一次标准碰撞所用时间为

由（1）（2）（3）式得

２．３    基于刘徽割圆术的向心加速度推导

接下来，可以引导学生分析圆内接正十二边形、圆内接正二十四边形……来求解量化平均加速度（图6，图7）。

在此以圆内接正十二边形为例设计问题引导学生探究。

（１）在一个标准碰撞过程中，台球桌边缘对台球的力的方向是怎样的？

（２）在一个标准碰撞过程中，台球的速度变化量为多少？

（３）完成一次标准碰撞的时间为多少？

（４）求出平均加速度的表达式。

（５）能不能通过圆内接正二十四边形探究平均加速度？

（６）通过以上探究你发现了什么规律？

割圆，从字面上理解，就是分割圆周。通过等分圆周，构造圆内接正多边形，在不断增加圆内接正多边形的边数基础上，用圆内接正多边形运动逐渐逼近圆周运动。通过以上探究，学生可以体会到，分割越细，越接近圆周运动，完成一次碰撞的时间越短，求出的平均加速度越接近于瞬时加速度，加速度的方向指向正多边形的中心即外接圆的圆心。

３    结束语

从生活中熟悉的台球运动构建理想化模型的抽象过程，培养学生的科学思维。沪科教版教材在第二章第二节的旁注中介绍了我国数学家刘徽首创的“割圆术”。本文引导学生采用刘徽“割圆术”的方法，将圆周运动看成无数个直线运动的组合，由浅入深，创设了具体的物理情境，启发学生步步思考，直抵圆周运动向心加速度的本质，为培养高中学生“微元法”这一高阶思维提供了一个很好的案例。刘徽割圆法的“微元”思想这一中国古老方法在向心加速度中的应用，也增强了学生的民族自豪感。

参考文献：

［1］李振宇，胡睿佳，娄青青．向心加速度公式的几种推导方法［Ｊ］．湖南中学物理，２０１５，３０（１）：６９－７０．

［2］张智．匀速圆周运动向心加速度公式推导方法［Ｊ］．湖南中学物理，２００９，24（７）：４０－４１．

［3］郭书春．关于刘徽的割圆术［Ｊ］．高等数学研究，２００７，10（１）：１１８－１２０．

［4］倪红飞．一种更符合学生认知规律的推导——向心加速度的教学建议［Ｊ］．物理通报，２０１７（４）：４３－４４．

（欄目编辑    蒋小平）