基于多智体强化学习的高效率货物列车运行动态调整方法

蒋灵明，倪少权

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.北京全路通信信号研究设计院集团有限公司，北京 100070)

铁路作为高效、绿色的陆地交通方式,是中国、日本、韩国和欧洲等国家和地区的主要公共交通运输方式。根据国际铁路联盟(UIC)发布的数据[1-2]:2017年全球铁路里程、客运和货运分别达到801 357 km、2 783亿人·km和8 991亿t·km。铁路特别适用于重型、散装和长途的大宗商品运输,例如货运铁路分别占美国和中国总运输份额的55%和50%[1]。而且,与公路运输(例如卡车)相比,货物列车平均减少了75%的温室气体排放与直接能耗[3]。

货运铁路网络的输运能力由速度、载重和运营效率决定。由于恶劣天气、临时限速、铁路建设或维护、自然灾害甚至列车事故等原因,货物列车的到达、出发和停留时间都会有所延误。更严重的是,延误会在一定范围内传播,导致大面积列车延误,降低运营效率[4]。本文重点关注原计划列车时刻表面临不同延误干扰下货物列车运营效率的提升,以实时或动态方式重新调度列车,使得延误或成本降至最低。因此,列车运行计划动态调整具有重要理论意义和应用价值,已成为研究热点[5-6]。

列车运行图调整或运行动态调整是一个NP完全问题。如文献[5-20]所述,列车运行图调整的恢复模型和算法涉及数学规划、启发式算法[7-8]、智能算法等。采用启发式算法的替代图模型或整数线性规划模型能够得到有效解[5,9-10],但在处理大规模调度问题时面临严峻挑战。与此同时,遗传算法、模拟退火法、粒子群优化算法和神经网络等智能算法在优化补偿列车时刻表的延误扰动方面也展现非凡实力[8,14-18]。

近年,作为一种先进智能算法——强化学习[21-22]被广泛应用于铁路交通管理中,如信号控制、列车调度或运行图调整[23-29]。强化学习结合了动态规划和有监督学习,适用于难以精确建模甚至无法数学建模的复杂环境。因此,强化学习是一种典型的无模型方法,它在获取优化的参数后,可以应用于不同环境[21],具有优良的泛化性。因此,强化学习算法(Q-learning等)已经在研究高速铁路(以下简称“高铁”)、城际列车和地铁的运行计划动态调整中发挥了重要作用[30-43],包括来自斯洛文尼亚[31]、英国[32-33]、荷兰[34-36]、印度[37-39]、韩国[40]和中国[41-43]的研究案例。

在上述研究工作的启发下,本文首次提出基于多智能体强化学习(Multi-agent Reinforcement Learning, MARL)突破大规模货物列车的运行计划动态调整难题,具有开创性参考价值。一方面,货物列车的规模(数量)远大于客运列车,其运行计划动态调整更为关键。然而,相较于高铁和地铁已经引入了多种智能型动态调整技术[30-43],货物列车的动态调整仍然以传统方法为主[44-50],且动态调整的效率具有一定局限性。另一方面,MARL在处理大规模货物列车运行计划动态调整问题上优势显著,而传统智能算法难以乃至不能实时或快速地处理。具体而言,货物列车运行计划动态调整将采用“多智能体”模式,而不是传统的“单智能体”模式[51]。多智能体算法被广泛应用于AlphaGo、智能多机器人、道路交通信号控制和分布式系统控制[27-28,51],具有并行优化和动态策略选择的优越性能。从原理上分析,MARL采用马尔可夫博弈(或随机博弈),引入了智能体之间交互(协作、冲突或组合)这一新自由度进行决策优化,而不是传统单智能体强化学习算法(Single-agent Reinforcement Learning, SARL)的马尔可夫决策过程。对应地,区段网内的货物列车可以组合成多个智能体,分别与环境进行交互,构建多智能体模式,而单智能体模式则是由所有列车组成的一个公共智能体与环境进行交互。因此,与单智能体算法相比,所提出的MARL的算法复杂度和计算时间呈现指数函数趋势下降。

本文首先阐述货物列车运行计划动态调整场景、基于MARL的运行计划动态调整算法,以及动态调整的实现过程;然后以包头—神木货运铁路为案列,进行模拟实验,验证运行计划动态调整方法的性能与效率,并与传统SARL进行性能比较;最后进行总结和讨论。

1 面向货物列车的多智体强化学习方法

1.1 场景描述

货物列车运行动态调整的铁路场景见图1:由双向运行(上行和下行方向)的单线轨道和4个车站(S1、S2、S3和S4)组成。由于货物列车整车较长,两个相邻站点之间设置为一个站间闭塞分区,共计3个站间闭塞分区。车站和站间闭塞分区的轨道都被定义为位置资源(详见2.2节),并按“1,2,3,…,14”进行编号排序。大多数情况下,货物列车(G1和G3下行列车,G2和G4上行列车)按照原计划时刻表在车站和站间闭塞分区之间有序运行。

图1 货物列车运行计划动态调整的铁路场景

为充分满足铁路运营的安全约束,对场景做以下近似理想合理约束:

(1)每列货物列车被视为一个质点,其位于车站轨道或站间闭塞分区,而不会同时占用站间闭塞分区和车站的轨道。

(2)每个车站由多条并行轨道(到发线)组成,可容纳列车数不超过并行轨道(到发线)数目。

(3)车站轨道和站间闭塞分区都必须满足唯一的资源占用约束,以确保列车运行的安全性,即该资源在某时刻只能为空闲状态或被一列列车占用。

(4)货物列车在车站可提前一定时间发车,以有效补偿延误干扰,而客运列车或地铁不允许。

(5)所有货物列车的运行速度相同(例如,包头—神木铁路速度为80 km/h),不考虑速度差异。

1.2 基于MARL的列车运行动态调整的原理与步骤

与SARL的“单智能体”模式不同,MARL采用“多个智能体”。为此,设计并定义两个不同的智能体,分别涵盖下行和上行货物列车,且这两个智能体与铁路环境交互,观察多个货物列车的状态(位置资源)和基础设施资源(车站、轨道和站间闭塞分区)的可用性。两个智能体(下行和上行列车)之间的相互作用以及与环境的交互见图2,每个智能体包含3个核心因素:状态、动作和奖励。MARL利用当前状态下的奖励(货物列车总延误时间最小化)积累学习经验完成Q-table更新,引导多智能体不断试错学习并逐步收敛,在安全运行条件下以最优动作(停止或前进)来最小化总延误时间。

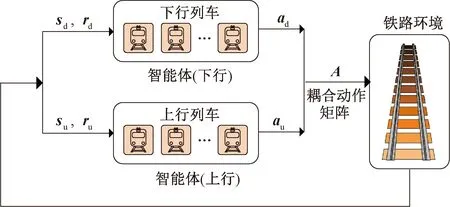
图2 两个智能体(下行和上行列车)之间的相互作用以及与环境的交互

在算法收敛和计算效率之间保持平衡的前提下,可以为特定场景设置更多智能体,而不仅局限于2个智能体。

图2中:sd、su分别为所有下行、上行货物列车的位置集;rd、ru分别为所有下行、上行货物列车的奖励函数矩阵;ad、au分别为所有下行、上行货物列车的动作矩阵;A为耦合动作矩阵。

在MARL方法中,智能体的状态、行动和奖励定义如下:

(1)状态定义为货物列车在每个时刻的位置资源及占用,即车站到发线或站间闭塞分区。图2中所有位置资源都按“1,2,3,…,14”进行编码和排序,每个智能体的状态由该智能体所包括的多个货物列车的位置集组成。

(2)动作定义为每列列车的两个可用动作(“停车”或“行驶”)。当考虑N列货物列车(N/2列下行列车和N/2列上行列车)时,每个智能体都有2N/2个行动集。假设任一列车(重车或空车)都可以在车站停车或行驶,但在站间闭塞分区必须行驶。

(3) 奖励定义为所有货物列车延误时间之和的倒数或者延误时间平方之和的倒数,即

( 1 )

或

( 2 )

由式( 1 )可知,每个智能体的奖励随着总延迟时间的减少而增加。当所有智能体到达最终状态时(即所有下行和上行列车都到达终点站),可以获得奖励。此外,还需设置一些惩罚机制,以促进MARL算法的收敛。例如,当迭代时间ti超过时间阈值而货物列车未能全部到达终点站时,训练过程中断且奖励为负值。因此,奖励函数进一步改写为

( 3 )

Tthreshold=Tspan+Tdelay+Tset

式中:ri为列车的奖励函数;β为放大常数,用于调控算法收敛速度;Tthreshold为阈值;Tspan为第一列车出发时刻与最后一列车到达时刻之间的时间跨度;Tdelay为所有列车干扰延误时间的总和;Tset为具体时间常数(设置为10 min)。另外,为避免局部最优和缩短训练时间,将时间阈值设置为MARL算法每轮训练结束的标志。

在场景描述和参数定义之后,进一步阐述基于MARL的列车运行计划动态调整的详细过程。两个智能体之间采用独立学习和相互竞争的混合策略,因此采用Q-learning方法来获得多个货物列车之间的最优动作(“停止”或“前进”)策略。对应于1.2小节,定义的两个智能体(下行和上行货物列车)的3个关键因素(状态、行为和奖励)可以进一步描述为

式中:S包括所有基础设施资源(车站轨道和站间闭塞分区),按顺序列为货物列车的可执行位置;A为由两个智能体的2N/2+2N/2=2(1+N/2)个单独操作所组成的动作集,假设下行列车和下行列车的数量(N/2)相同。同样场景下,单智体模式的SARL方法却具有2N个独立的动作。

经过对比,不难发现:MARL方法的复杂度由O(2N)降到O[2(1+N/2)]。假设面向22列货物列车(第3节),MARL的算法复杂性或计算时间降低为SARL计算时间的约1‰(即1/1 024)。因此,该MARL方法能够高效、实时地完成货物列车的运行计划动态调整任务,特别是大规模动态调整。

此外,每个智能体的动作通过ε贪婪策略进行决策,以ε为探索率决定执行动作的概率,即

( 4 )

( 5 )

式中:μ(t,ai|si)表示第i个智能体(i=d或u)在时间t和状态si下目标动作集合;A(t,si)为在时间t状态si的所有可能动作集;rand为标准正态分布;a*为与时刻t时状态si中最大值Q对应的动作;其余参数见表1。

由式( 5 )可知:随着训练片段的增加,ε逐渐减小并接近于零,即随着训练代数增加,智能体倾向于使用学习经验,从而产生最优动作集。

Q-learning通常基于状态和动作来构造Q-table的更新规则。在基于MARL的列车运行计划动态调整过程中,状态由列车数量(N)、车站数量(M)和时间跨度Tspan组成,所有状态的数量达到MN×Tspan。因此,Q-table中元素数量增加到MN×Tspan×2(1+N/2)。随着列车规模增加,Q-table中的元素数量呈现出爆炸性增长。为降低复杂度,结合时间和动作构建Q-table,则第i个智能体的Q-table为

Qi(t+Δt,ai)=Qi(t,ai)+

α[ri-Qi(t,ai)+γgmaxQi(t,:)

( 6 )

式中:Δt为时间步长;ri为第i个智能体在状态si执行动作ai而获得的奖励。maxQi(t,:)为时刻t的最大Q值。表1和算法1详细给出了的MARL的参数定义和算法步骤。

算法1基于MARL的列车运行动态调整算法

输入:α,β,T_table,Q_table,max_episode,S_matrix,delay_time,delay_point;

输出:opt_plan;

输入(Train_environment,Q_table,episode)

1: forepisode=1:max_episode

2: 输入(t,states,done)给上下行智能体;

3: while !done do

4: foragent_i:

5:state_i=states(i);

6: [action_i,res_i] =get_act_res(t,state_i);

7:actions= [train_i],ress= [res_i];

8:check_action_res(actions,ress);

9: [states_,rewards,done] =step(t,states,

actions,ress);

10: foragent_i:

11:Q(t,action_i,agent_i) =

12:Q(t,action_i,agent_i) +α[reward_i+γmaxQ(t,action_i,agent_i)];

13:t=t+ 1;

14:states=states_;

15: end

16:opt_plan=greedy(Q_table);

17:plot(opt_plan);

18: end

2 基于多智体强化学习的货物列车运行计划动态调整案例

2.1 包头—神木铁路中等规模的动态调整

万南场—东胜区段货物列车运行计划动态调整场景见图3,这是包头—神木煤炭货运铁路主干部分。该区段由91.4 km的双向单线轨道组成,设有9个车站和8个站间闭塞分区。对应地,万南场—东胜区段可构建69个位置资源,由车站轨道(到发线)和站间闭塞分区组成;计划期间共有22列货物列车,上行和下行各为11列。

为比较MARL与SARL的性能,首先研究一个中等规模货物列车的运行动态调整。中等规模货物列车运行动态调整的3种算法(MARL、SARL和FIFO)性能比较见表2,如表2所示,选取1列或3列列车晚点场景下的5种延误扰动条件,并进行动态调整测试。本文聚焦延误扰动(表2)为决策者已知的场景下,利用MARL与SARL方法实现货物列车的运行动态调整。

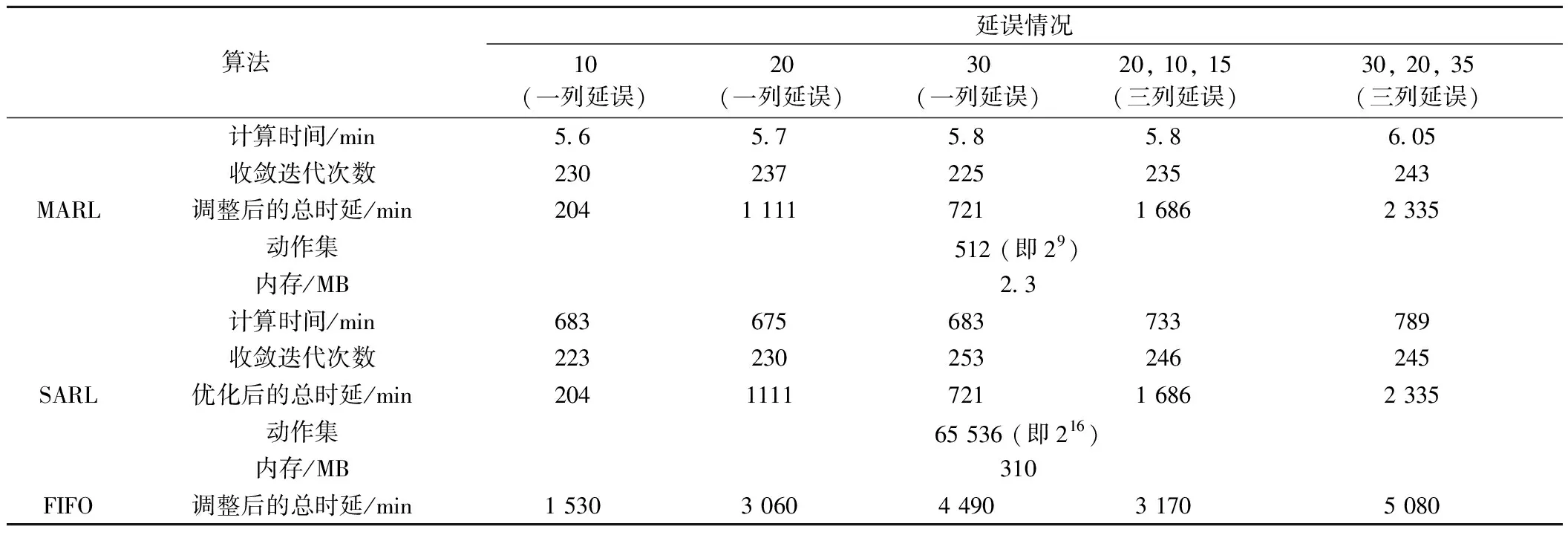
表2 中等规模货物列车运行动态调整的3种算法性能比较

本文采用通用计算机(AMD Ryzen 7 5800X 8核3.79 GHz CPU和64GB RAM)完成货物列车运行动态调整程序的测试。如表2所示,MARL方法的收敛迭代均为250次以内,且对所有扰动条件下的优化调整均收敛有效。进一步选择两种扰动情景进行详细分析,见表3。如图4(a)和图4(b)所示,在两种扰动条件下(一列和三列延误),MARL方法收敛稳定后的最佳总延误时间分别为721 min和1 686 min。值得指出的是:图4(a)和图4(b)中迭代过程中产生了比最终收敛结果更小的延误时间。这是因为将时间阈值设置为MARL算法每轮训练结束的标志,以避免局部最优和缩短训练时间。在每轮训练中,当训练时间超过时间阈值且存在列车未到达终点站时,训练被强制停止而未到达终点站的列车不计算终点站的延误时间,因此出现最终收敛结果的更小延误时间,这些更小延误时间不能作为动态调整的有效解。

表3 中等规模货物列车运行动态调整的延误扰动条件

图4 中等规模货物列车的MARL方法收敛结果和动态调整前后的货物列车运行图

图4(c)和图4(d)展示了两种扰动条件下经过列车运行动态调整后的时间表。不难看出,两种条件下动态调整获得的时间表均满足唯一的资源占用约束。因此,实验结果表明MARL方法能够有效处理大规模的运行动态调整。

为了验证MARL方法处理货物列车运行动态调整的高效率,同时采用了SARL方法来处理表2中的延时扰动问题。与图4所示的扰动情景(1列延误列车和3列延误列车)相同,SARL方法处理重新调度后的时刻表见图5。显然,对于不同的扰动条件,MARL和SARL方法都可获得相同总延误时间。

图5 中等规模下货物列车的SARL方法收敛结果和动态调整前后的货物

更进一步,表2提供了MARL和SARL方法之间的全面性能比较,例如计算时间、操作集和内存需求。与MARL相比,SARL方法的动作集增加了27倍,达到 65 536。 因而SARL计算时间高达675 min甚至更多,而MARL的计算时间大幅度减少到5～6 min,不到SARL的1%。显然,MARL方法极大地提升了计算效率,这种优势对于3.2节中的大规模的动态调整更为明显。

此外,引入先进先出(FIFO)算法以提供更加全面的性能比较,它对延误列车采用整体平移策略,不能通过超车方式进行调整。与FIFO算法相比,MARL方法的总延迟时间降低了44%～86%。

2.2 包头—神木段大规模货物列车运行动态调整

为了在更大范围内验证运行计划动态调整能力,利用MARL方法对全部22列货物列车进行动态调整,即下行和上行方向各11列货物列车。

同样,在上述铁路环境下,选择了1列和3列延误列车的两种扰动条件。大规模货物列车(22列)运行计划动态调整的收敛结果如图6(a)和6(b)所示。经过250或300次训练后,最佳总延迟时间分别为721、 1 689 min,两种干扰条件见表4。相应地,图6(c)和图6(d)显示了两种延误扰动下经动态调整优化后的列车时刻表。两种扰动条件下,受延误影响的22列列车在计划动态调整后的时刻表仍满足对资源占用的唯一约束。

表4 大规模动态调整下(22列)延误扰动条件

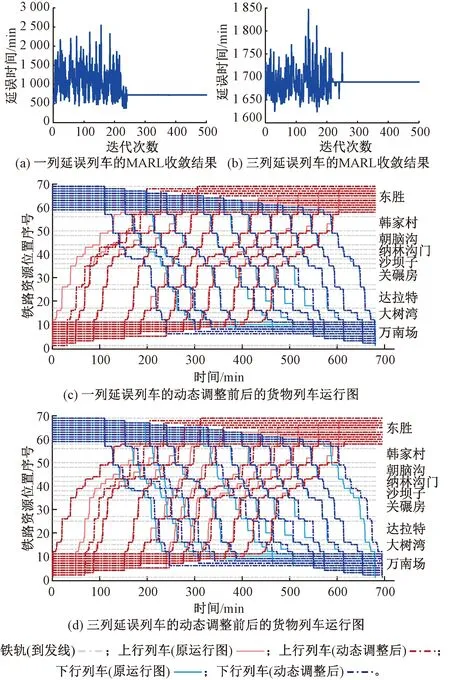
图6 大规模货物列车(22列)的MARL方法收敛结果和动态调整前后的货物列车运行图

根据表5和图6的统计与分析结果,MARL方法能够有效解决延误干扰下大规模货物列车的运行计划动态调整,并得到最小总延误时间。然而,若采用SARL替换MARL来实施动态调整,动作集从4 096(即212)指数上升至4 294 967 296(即222),此时该通用计算机已经无法在短时间内完成优化过程。根据表2和表5对此时SARL所需的计算时间和内存进行预测:该通用计算机需要耗时3 469 d(即4 995 600 min),几乎难以完成任务。这一结论与2.2节的理论分析是一致的:MARL使得算法复杂度从O(2N)到O[2(1+N/2)]成指数趋势级降低,因而计算效率以2(N/2-1)倍显著提高。

表5 大规模货物列车(22列)运行动态调整的MARL与SARL性能比较

值得指出的是,若采用高性能计算服务器可以进一步减少大规模列车运行计划动态调整下的MARL计算时间(例如仅需几分钟),提供实时模式服务。然而,此时SARL方法仍需数十、数百小时,依旧无法完成以实时或快速的大规模货物列车运行动态调整任务。

3 结论

针对大规模货物列车运行动态调整问题,本文提出了一种高计算效率的MARL方法。颇具创意的是,该MARL方法将上行和下行货物列车设计为两个不同的智能体,从而使其算法复杂度比单智能体算法大幅度。以包头—神木货运铁路为例,在处理22列货物列车和9个车站的大规模动态调整案例,该MARL方法能够获得稳定收敛的最小总延误时间和可行的列车运行调整方案。但由于所需计算时间巨大,传统SARL方法不可能在短时间内完成大规模运行计划动态调整任务。因此,本文提出的基于MARL方法的货物列车运行计划动态调整有望为大运量、复杂网络的铁路货物列车调度问题提供一种有效和有力的解决方案,从而显著提高货运铁路的运营效率。