高速铁路闭塞分区布置优化研究
欧俊杰,柏 赟,骆 晖,刘海东,杜慎旭
(1.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室,北京 100044;2.中铁第四勘察设计院集团有限公司 线站处,湖北 武汉 430060)
0 引言
我国高速铁路采用准移动闭塞信号制式,这种制式将行车区间划分为若干闭塞分区,相邻列车间隔数个闭塞分区追踪运行。分区长度过长,会增大列车追踪间隔,并降低线路通过能力;反之,分区长度过短则会影响列车追踪安全,同时也会增大分区信号机(标志牌)以及轨道电路等基础设施建设成本。因此,合理划分高速铁路闭塞分区对于提高铁路线路通过能力、保证列车运行安全与降低线路建设成本具有重要意义。
对于闭塞分区布置优化问题,国外学者大多针对地铁或普速铁路进行研究,对高速铁路闭塞分区优化问题涉及较少。Ke 等[1]以列车运行能耗最小为目标,利用蚁群算法优化地铁固定闭塞分区布置方案。Burdett[2]从数学规划的角度分别以通过能力最大、建设成本最小为目标构建铁路闭塞分区布置优化模型,并求解最优布置方案。Vignali 等[3]利用OpenTrack 软件仿真计算不同闭塞分区布置方案下的车站追踪间隔,求解可满足通过能力需求的最佳闭塞分区布置方案。
相比普速铁路,高速铁路在布置闭塞分区时需额外考虑列车过电分相、追踪安全等更复杂的约束。针对准移动闭塞条件下的高速铁路闭塞分区优化问题,高国隆等[4]利用遗传算法对高速铁路区间闭塞分区分界点位置进行优化,在不增大建设成本的基础上提高线路通过能力。刘海东等[5-6]采用模拟手工设计闭塞分区的启发式仿真算法求解最小区间闭塞分区数量,并进一步设计改进的差分进化算法求解准移动闭塞分区布置优化问题。
轨道电路需在闭塞分区布置方案确定后,根据地形条件对闭塞分区进行分割。上述研究在优化闭塞分区布置方案时未能充分考虑地形条件对轨道电路划分的影响,所求得的闭塞分区设计方案不能较好地节省轨道电路分割成本。为此,张陶等[7]模拟手工布置方法提出轨道电路自动分割算法,刘菁华[8]使用模拟退火算法,求解给定闭塞分区布置方案下的最小轨道电路分割点数量与分割方案,但二者均未考虑优化调整闭塞分区方案对轨道电路分割的影响。
综上所述,既有研究在优化闭塞分区方案时较少考虑轨道电路分割成本。因此,考虑高速铁路轨道电路的实际分割要求,构建模型优化闭塞分区分界点的数量与位置,在保证线路通过能力与行车安全的前提下,降低轨道电路分割成本以及分区信号机(标志牌)建设成本。
1 高速铁路闭塞分区优化方案分析
高速铁路线路通常使用标志牌作为分界点区分两相邻闭塞分区。各闭塞分区内设置若干轨道电路区段用以检测列车占用情况,闭塞分区布置方案示意图如图1 所示。考虑到轨道电路工作的稳定性,其长度通常存在上限。因此,应在闭塞分区的分界点或轨道电路极限长度处设置轨道电路分割点,以保证轨道电路的正常工作。
闭塞分区分界点的布设数量Ns与位置不仅决定了分区标志牌或信号机建设成本,也对轨道电路分割成本产生影响。如图1 中,闭塞分区分界点处需设置轨道电路分割点,分界点数量与轨道电路分割点数量直接相关。同时,分界点布设位置也会影响轨道电路分割点数量,如图1 中方案一分界点布设位置未能充分利用轨道电路极限长度,调整为方案二后可减小1 个轨道电路分割点。

图1 闭塞分区布置方案示意图Fig.1 Schematic diagram of block section layout
在设计闭塞分区方案时不能为节省标志牌或信号机建设成本而过于增大闭塞分区设计长度,还需要考虑列车运行间隔约束。高速铁路列车以闭塞分区的占用情况作为是否继续追踪前车运行的依据,闭塞分区设计过长会增加列车出清分区时间,从而增加列车追踪间隔,使闭塞分区布置方案无法满足线路通过能力需求。
除考虑建设成本与线路通过能力对区间闭塞分区设计的影响外,还应考虑设计规范对闭塞分区分界点设计位置与设计长度的要求,以及列车运行安全。例如,高速铁路列车通过电分相时的运行安全,确保列车能够在闭塞分区标志牌前因故停车时能够安全驶出电分相,列车在上坡处闭塞分区标志牌前因故停车时能够克服坡道阻力顺利启动等。
综上,通过优化闭塞分区分界点的布设数量Ns与位置,得到满足设计规范、行车安全与通过能力需求等约束条件,且分区标志牌/信号机建设成本与轨道电路分割成本更优的闭塞分区布置方案。
2 高速铁路闭塞分区布置优化模型
2.1 优化目标
以降低信号机(标志牌)建设成本与轨道电路分割成本为优化目标,设计满足通过能力需求、设计规范与行车安全等条件的闭塞分区布置方案,优化目标如公式 ⑴ 所示。

式中:Z为闭塞分区布置方案建设成本,元;α为信号机单位建设成本,元;β为轨道电路分割点单位建设成本,元;Ns为闭塞分区分界点数量,个;Ng为轨道电路分割点数量,个。
2.2 约束条件
布置闭塞分区的约束条件分为3 类:闭塞分区分界点位置约束、轨道电路分割长度约束、追踪间隔与运行安全约束,其中追踪间隔与运行安全约束需结合列车仿真进行计算。
2.2.1 闭塞分区分界点位置约束
闭塞分区分界点必须安放在规定的限界内,即位于运行后方车站反向进站信号机和运行前方车站进站信号机之间,且不能与其他既有信号机重合,如公式 ⑵ 所示。

式中:为运行后方车站出站信号机位置;为运行前方车站进站信号机位置;为区间其他固定信号机位置;为闭塞分区分界点位置。
闭塞分区长度必须要在合理的范围内,且所有闭塞分区长度之和与区间长度相等,各闭塞分区长度需要满足的条件[9]如公式 ⑶ 所示。
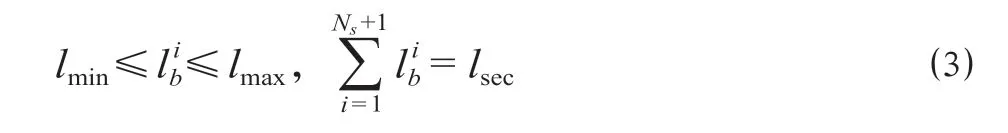
式中:为闭塞分区长度,m;lmin为闭塞分区最小长度,通常取300 m;lmax为闭塞分区最大长度,通常取3 000 m[9];lsec为区间长度,m。
一般情况下,闭塞分区分界点与电分相的距离不宜小于550 m[10],如公式 ⑷ 所示。

式中:为电分相左断电标位置;为右合电标位置。
同时,车站第三接近分区和第一离去分区不能放置电分相,即任意分相的右合电标位置不能超过第三接近分区分界点,如公式 ⑸ 所示。

式中:为第三接近分区分界点位置;Nf为区间电分相数量。
任意分相的左断电标位置须超过第一离去信号机,如公式 ⑹ 所示。

式中:为第一离去分区分界点位置。
在列车运行过程中,当列车因前方分区被占用需在闭塞分区前停车时,若该闭塞分区分界点位于较大上坡处,列车可能因启动牵引力不足而无法重新启动,则分界点后方坡道不可大于列车正常启动坡度,如公式 ⑺ 所示。

式中:为分界点后方坡度;imax为列车正常启动最大坡度。
2.2.2 轨道电路分割长度约束
轨道电路在有砟/无砟道床,以及不同轨道结构类型的区段有不同的极限长度要求[11],如公式⑻所示。

式中:为轨道电路分割点位置;lcir为轨道电路极限长度,m。
2.2.3 追踪间隔与运行安全约束
闭塞分区布置方案需兼顾线路的设计通过能力与安全运行要求,具体包括区间追踪间隔、车站出发间隔、车站到达间隔和车站通过间隔满足能力需求,以及列车追踪码序信息可安全预告前车位置。
CTCS-2/3 级列车运行控制系统的轨道电路传输码序信息为:L5—L4—L3—L2—L—LU—U—HU。区间追踪间隔与码序约束示意图如图2 所示。为保证列车安全追踪运行,列车所能接收到的最大预测距离须满足追踪安全距离要求[12],如公式 ⑼所示。

式中:Node为码序数量,通常为7 (L5 码序备用);为列车当前追踪码序上的闭塞分区长度,m;lbrake为列车常用制动距离,m;lf为各种设备动作时间及司机反应时间内走行距离,m;lsafe为安全防护距离,通常取100 m。
对于区间内闭塞分区i对应分界点,其追踪间隔的计算如图2 所示,此时前方列车位于闭塞分区i的终点处,后方列车与分界点的距离大于安全距离、制动距离与附加时分内列车运行距离之和,定义为满足以上追踪条件的最近位置处,则点的区间追踪间隔Ii[12],如公式 ⑽ 所示。车站通过间隔与区间追踪间隔的计算方法相同,即将车站内区域视为一个闭塞分区。
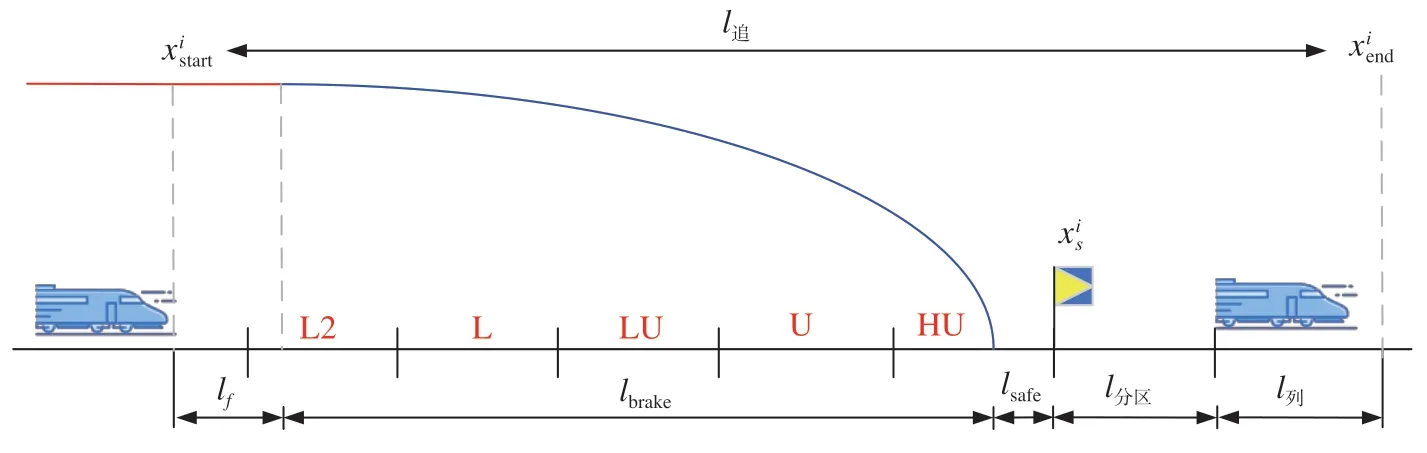
图2 区间追踪间隔与码序约束示意图Fig.2 Schematic diagram of tracking interval and code sequence constraint

式中:H为线路设计追踪间隔,s;f(x)为列车在区间不同位置处的运行时间数据,可根据线路数据与列车数据通过仿真获得;为闭塞分区i的终点位置;为以为目标且满足追踪条件的最近位置。
第一离去分区长度约束示意图如图3 所示,当前方出站列车出清第一离去信号机时,后车即可办理发车作业,并生成以第一离去信号机为行车许可终点的控车曲线(图3 中虚线),后车实际之间的列车运行时间即为分界速度曲线如图中实线所示,为充分利用车站道岔限速大小以及防止列车出站过程中因“触碰”控车曲线而减速,需满足公式 ⑾ 约束[12]。

同时,还需考虑第一离去闭塞分区长度对列车出发间隔的影响[12]。图3 中出站信号机开放时前方列车位置与后方站台停车位置间的距离为列车出发追踪间隔距离,该距离包括安全距离lsafe,出站信号机与反向进站信号机间隔距离lsig,第一离去分区长度lsec,出站作业时间内列车运行距离lf,列车长度ltrain。列车出发间隔Id的计算过程参照区间追踪间隔Ii。

图3 第一离去分区长度约束示意图Fig.3 Schematic diagram of length constraint of first block section to leave the station
第二接近分区长度约束示意图如图4 所示。列车在区间追踪需进站停车时,在到达第二接近信号机前按图4 中控车曲线运行。此时默认前方进站信号机关闭,列车不可进入车站,目标停车点为进站信号机前方(附加一定安全距离)。当列车到达第二接近信号机后,更新前方车站信息,若接车进路未准备完毕,则继续按控车曲线运行,如图4中虚线所示;若接车进路准备完毕,则重新生成进站运行曲线控制列车运行[12]。可知第二接近信号机位置决定列车到达间隔大小Ia,其计算过程参照区间追踪间隔Ii。

图4 第二接近分区长度约束示意图Fig.4 Schematic diagram of length constraint of second block section to approach the station
3 模型求解算法设计
上述模型以闭塞分区分界点里程作为变量,由不同的取值组合成闭塞分区布置方案,较大的计算规模使其难以用数学优化方法求解,此外,轨道电路分割点需结合闭塞分区布置方案与线路条件进行确定,难以用解析法直接求解。为此,将闭塞分区布置优化问题分解为两阶段进行求解。第一阶段利用免疫遗传算法生成并优化闭塞分区分界点位置,在此基础上,第二阶段利用轨道电路自动分割算法生成完整的闭塞分区布置方案,并计算建设成本作为免疫遗传算法的寻优指标。
3.1 闭塞分区优化算法
(1)个体编码。采用长度为n的染色体(x1,x2,…,xn)来表示闭塞区间布置方案,以实数形式进行编码,染色体中的各个体基因(i=0,1,…,Ns)代表着闭塞分区分界点的具体坐标。
(2)初始种群生成。质量较好的初始种群可加快算法的收敛速度与求解效率,初始种群生成算法是在确定种群规模Q后,根据区间长度lsec以及最大、最小闭塞分区长度lmax,lmin,随机生成可行的闭塞分区分界点数量以此等分区间得到单位基本长度s,并逐次在[s×k-r,s×k+r]范围内随机产生闭塞分区分界点坐标,其中k∈[1,Ns],r为[100,300]内的随机数。
(3)适应度函数计算。以闭塞分区分界点数量以及轨道电路分割点数量最小作为优化目标,定义适应度函数如式 ⑿ 所示。
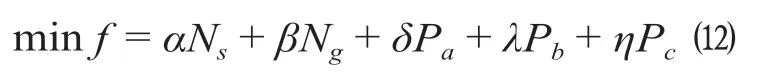
式中:Pa,Pb,Pc分别表示个体中不符合2.2 节中3 类约束的闭塞分区分界点数量;δ,λ,η为相应的惩罚因子。
(4)免疫操作。免疫算法以个体的亲和力作为个体克隆选择的评价指标,亲和力由解与问题的适应值以及解与解之间的相似度计算;执行交叉操作时,考虑到不同个体闭塞分区布置数量存在差异,算法首先随机取出需要交配的个体对,再选取闭塞分区数相同的个体实施交叉操作,交换各自的指定基因,形成新的个体;执行变异操作时,以变异概率p随机对某个基因上的多个闭塞分区分界点位置进行0~100 m 的调整。
3.2 轨道电路分割算法
高速铁路闭塞分区长度在2 000 m 左右,使用的ZPW-2000A 轨道电路因所处道床类型与地形条件不同,其极限长度为500 m 到1 400 m 不等,因轨道电路长度小于闭塞分区长度,各闭塞分区需由多段轨道电路区段组成,即需要对闭塞分区进行分割。
通过模拟人工轨道电路分割方法,基于不同地形条件下的轨道电路极限长度取值,按最小化分割点数量的原则布置轨道电路分割点,轨道电路自动分割算法流程如图5 所示。算法核心是求解每次分割轨道电路的最大长度,由于单次分割长度内可能存在多种地形条件,按分割范围内地形特征划分3种情形。
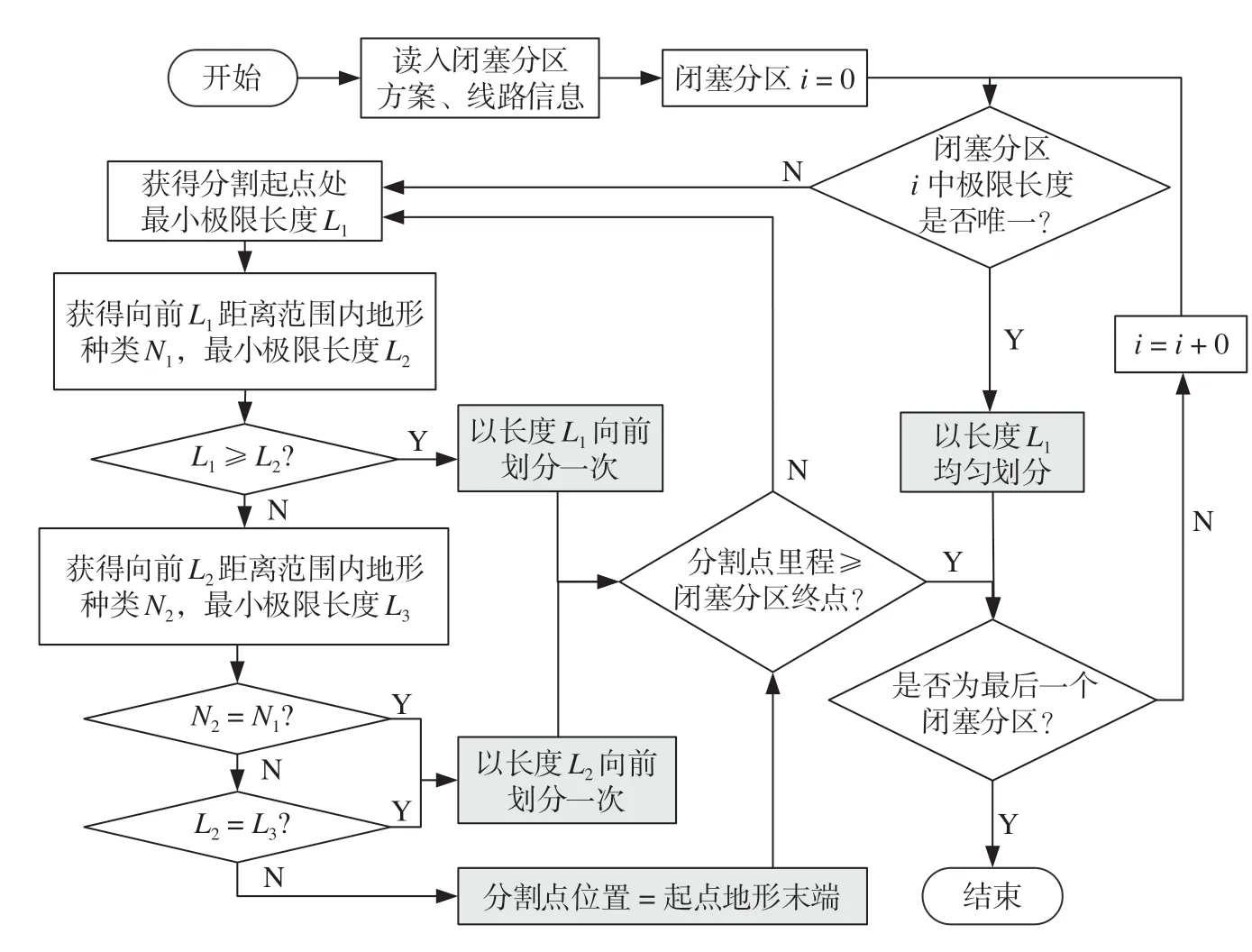
图5 轨道电路自动分割算法流程Fig.5 Automatic segmentation algorithm for track circuit
(1)仅存在单一地形条件。若是单一地形即可按照该地形条件下轨道电路极限长度均匀分割闭塞分区,而后从下一闭塞分区起点处执行下一轮操作。
(2)非单一地形条件且分割起点处极限长度更小。若该闭塞分区不是单一地形,此时判断当前分割起点处极限长度覆盖范围内是否有极限长度更小的地形,若没有,则说明可按分割起点处极限长度执行本次分割。
(3)非单一地形条件且分割范围内存在更小极限长度。若当前极限长度覆盖范围内存在极限长度更小的地形,此时判断从当前起点至更小的极限长度范围内,是否包括了使极限长度缩小的地形。若包含,则说明必须以更小的极限长度执行下次分割;若不包含,则说明极限长度更小的地形起点存在于分割起点处极限长度与更小的极限长度之间,此时应以当前地形末端位置(下一地形起点)作为分割点,即可保证不超过当前地形极限长度取值,且不影响下一地形的分割,同时可最大化利用轨道电路极限长度。
4 案例分析
4.1 基础数据
选择某高速铁路长度为39.97 km 的A—B 区间为例进行验证,以案例线路中CRH3型动车组作为仿真列车,CRH3 型动车组数据如表1 所示。优化目标中单位成本系数α,β分别设为1 000 与18 000[13]。

表1 CRH3 型动车组数据Tab.1 Data of CRH3 EMU
不同道床类型的轨道电路极限长度如表2 所示[11],表中标准分路电路取0.15 Ω 表示线路为无砟道床,取0.25 Ω 表示线路为有砟道床。
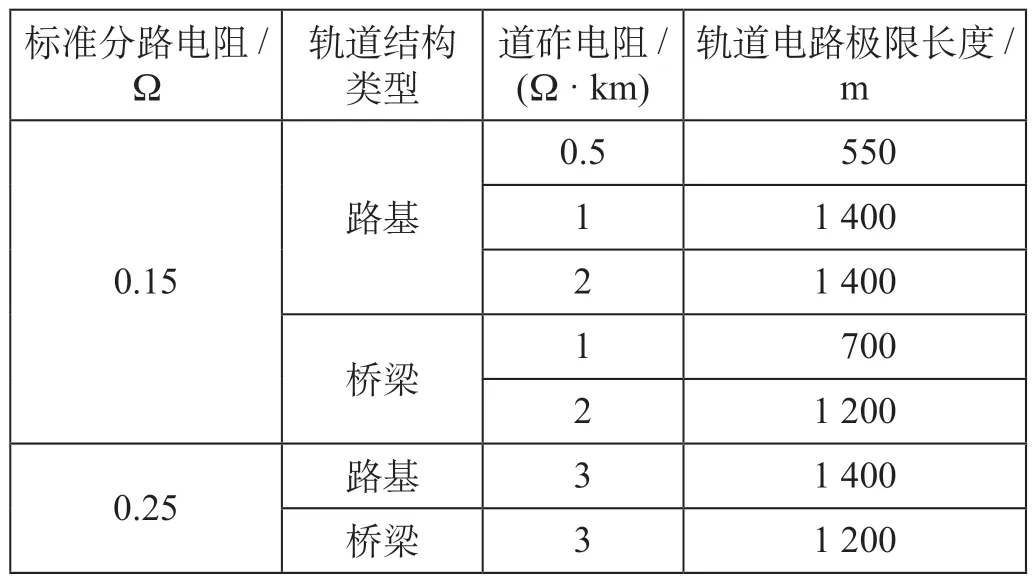
表2 不同道床类型的轨道电路极限长度Tab.2 Length limit of track circuit for different types of track bed
4.2 计算结果分析
考虑到实际高速铁路闭塞分区设计以提高通过能力为主要目标,为保证所求解闭塞分区布置方案能在不降低通过能力的前提下减少建设成本,在求解布置方案时不改变第一离去、第二接近分界点位置。
根据4.1 节基础数据对闭塞分区分界点位置与数量进行优化,优化前后闭塞分区布置方案对比如图6 所示。由图6 可以看出,红色实线标记框处调整后的轨道电路分割点数量减少,同时在图中蓝色虚线标记框处增加一个闭塞分区分界点。经计算,优化后建设成本降低了6.3%。
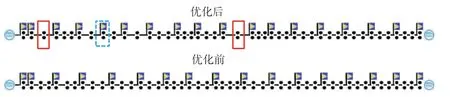
图6 优化前后闭塞分区布置方案对比Fig.6 Comparison of block section layout before and after optimization
优化前后闭塞分区布置方案数据如表3 所示。由表3 知,优化后闭塞分区分界点数量由15 个增加至16 个。通过调整除第一离去、第二接近分界点外的其余分界点位置,可使轨道电路分割点数量由46 个减少至43 个。
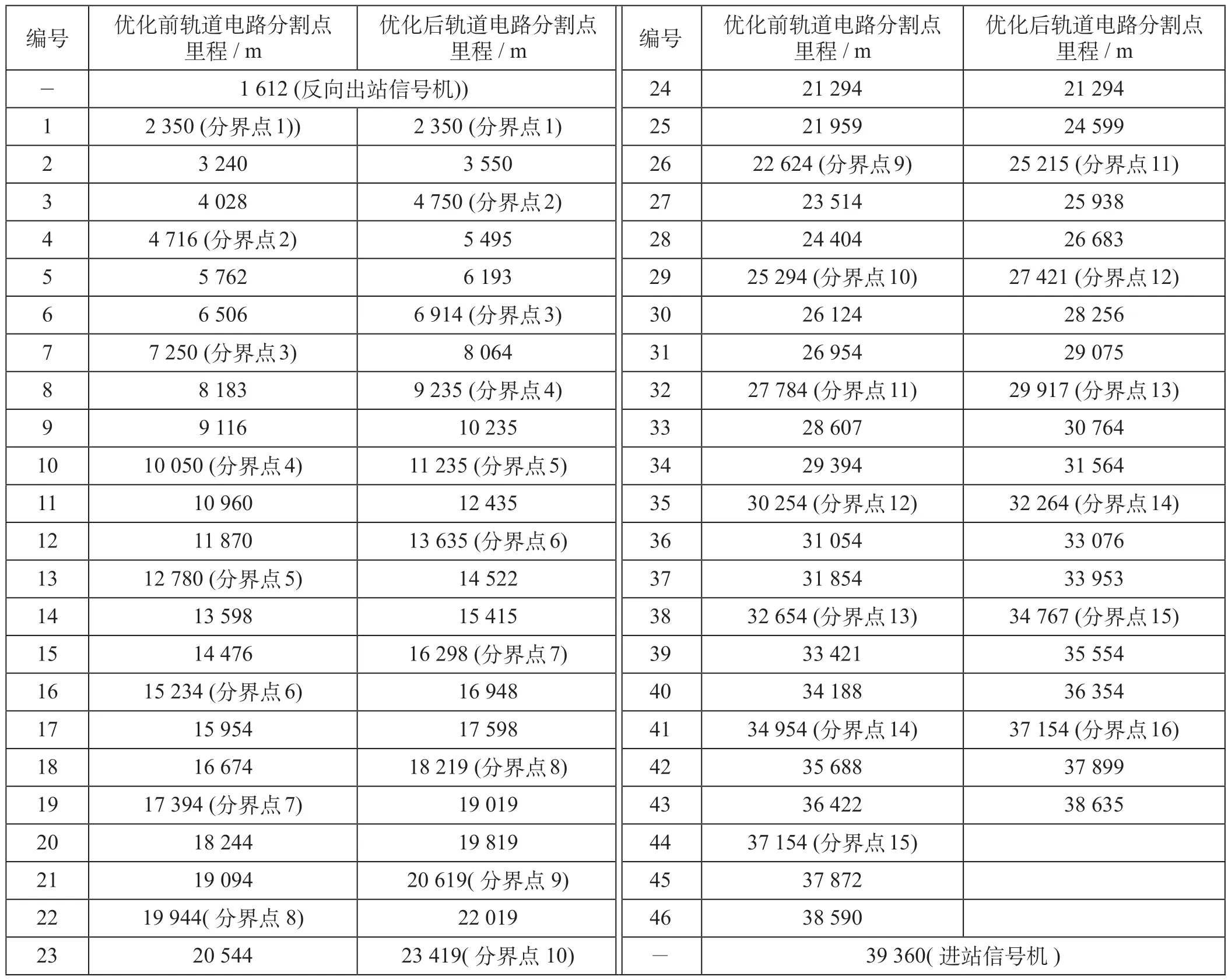
表3 优化前后闭塞分区布置方案数据Tab.3 Data of block section layout before and after optimization
追踪间隔检算结果对比如表4 所示。因优化后增加一个闭塞分区分界点,区间追踪间隔减少4 s,使区间通过能力提高了2.3%,但受车站追踪间隔的影响,线路通过能力保持不变。说明优化后闭塞分区布置方案可在不降低线路通过能力的前提下,优化闭塞分区建设成本。
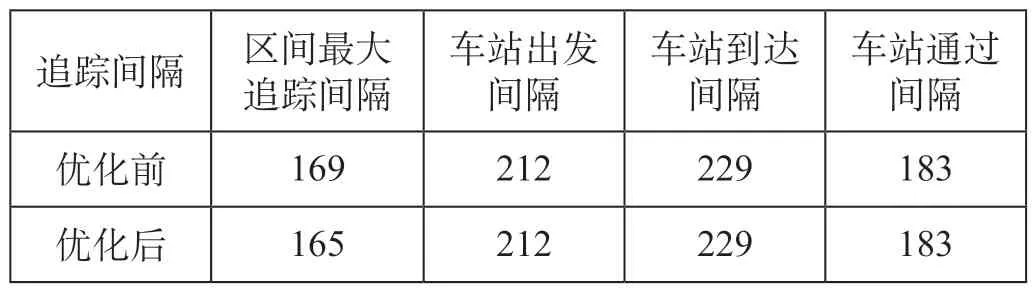
表4 追踪间隔检算结果对比 sTab.4 Comparison of tracking interval check results
5 结束语
在分析高速铁路闭塞分区布置的目标与影响因素基础上,构建准移动闭塞方式下的区间闭塞分区布置优化模型,设计闭塞分区优化算法与轨道电路自动分割算法,实现了高速铁路闭塞分区布置的优化。案例分析结果表明:优化后闭塞分区布置方案不仅满足设计规范与行车安全约束,而且在不降低线路通过能力的前提下,使闭塞分区建设成本降低了6.3%,区间通过能力也得到一定程度的提高。在给定建设成本上限约束的情况下,可进一步研究以线路通过能力最大化为优化目标的闭塞分区布置方法;另外,闭塞分区需在线路设计方案确定后进行布置,两者间具有设计耦合关系并会影响线路通过能力与综合建设成本,线路平纵断面设计与闭塞分区布置协同优化问题也可作为下一步的研究方向。

