结合长短期混合特征的均衡风缸控制系统健康状态评估方法
高殿柱,彭 军,王胜男,张晓勇,杨迎泽,黄志武
(1.中南大学 自动化学院,湖南 长沙 410083;2.中南大学 计算机学院,湖南 长沙 410083;3.轨道车辆制动技术湖南省工程实验室,湖南 长沙 410075)
DK-2制动机已成功装备于SS4B、TM3等电力机车,均衡风缸控制系统是实现制动机制动与缓解功能的关键系统,其健康状态对于机车安全运行有重要的指示作用[1]。目前,DK-2制动机配备的健康管理系统主要用于实现数据实时监测与故障诊断功能,但仍缺乏对系统内部部件的数据监测,如制动电空阀、缓解电空阀等,无法实现全生命周期的健康状态评估,根据剩余使用寿命实现故障预警与视情维修。
预测与健康管理技术是实现健康状态评估的重要手段[2],已被引入制动系统研究中[3]。根据模型的不同可以将剩余使用寿命预测方法分为4种:物理模型方法、统计模型方法、机器学习方法和混合模型方法[4]。
物理模型方法通过分析系统部件失效机理和机械损伤原理,建立描述此类过程的数学模型,实现系统的剩余使用寿命预测[5]。文献[6]引入粒子滤波技术,建立基于物理机理的气动阀门模型,并进行仿真实验证明该方法在有限传感数据场景下的鲁棒性。文献[7]通过诺顿定理对部件的老化过程进行描述,并结合卡尔曼滤波和粒子滤波实现剩余使用寿命预测,但该方法没有考虑不同工作模式对部件老化物理模型构建的累积影响。
统计模型[8]评估方法利用部件的观测数据建立统计学模型,采用概率方法以概率密度函数的形式拟合观测值,获得预测结果。文献[9]假设设备的未来状态值是过去观测值和随机误差的线性函数,利用自回归模型对部件的退化过程进行建模及预测。在此基础上,文献[10]引入3种外部变量对自回归模型进行优化。
机器学习方法可以仅根据历史数据且无需理解系统复杂的老化原理对剩余使用寿命进行预测[11],其预测结果相比于文献[9-10]方法更为准确。文献[12]针对部件的剩余使用寿命问题展开研究,在构建振动敏感时频特征向量后,利用k-最近邻分类器根据训练集的邻域信息对样本进行寿命预测,但是此模型的效果依赖于k值的选取,具有不确定性。文献[13]针对动车组随机悬架动力学,引入神经网络实现对随机动态系统的精准建模,实现预知和健康管理提高动车组的安全性和可靠性。
考虑上述方法的互补性,学者们开始研究混合模型寿命预测方法,即通过集成不同预测模型实现优缺点的互补[14]。此类方法至少混合了物理、统计、机器学习方法中的一种,内部至少包含两个模型。文献[15]将基于机器学习的预测模型与基于物理模型的方法融合进行系统状态预测。在贝叶斯学习的基础上,利用粒子滤波进行系统状态估计和参数辨识,并进一步利用机器学习预测模型估计未来测量值。文献[16]从振动传感器信号中提取特征,利用最小二乘支持向量回归预测特征趋势,通过隐马尔科夫模型对系统退化过程中不同健康状态进行离线训练与预测。
综上所述,基于物理模型的方法需要对研究对象的老化过程进行建模[17];基于统计模型的方法需要监测数据满足特定的分布;基于机器学习的方法则缺乏一定的解释性。在综合考虑部件老化特点、数据特点、物理模型建立难度后,基于混合模型的方法通过选择恰当的混合策略进行寿命预测,可表现出更好的预测性能[18]。
对于工作在多种模式切换状态下的均衡风缸控制系统而言,不同部件的物理参数演化趋势可能不同,老化过程较为复杂,难以进行具有普遍性的物理建模,并保证监测数据的分布完全符合统计模型要求,基于物理模型和统计模型的方法难以提供很好的预测性能。因此,本文采用机器学习方法进行部件剩余使用寿命预测,不进行物理模型建模。考虑技术可行性和预测准确性,通过分析系统内阀类部件的失效机理,选取其驱动电流作为数据支撑,提取反映部件健康状态的物理指标,增加模型的解释性。
然而,单一的机器学习方法应用于均衡风缸控制系统的健康状态评估仍面临两大挑战:首先,制动机均衡风缸控制系统是离散变量与连续变量同时存在的多模式混杂系统,系统可工作在单工况及多工况环境下,部件当前剩余使用寿命与其历史的累积经历有关,不同模式下部件产生的退化程度不同,本身的特征水平也不同。通过结合系统模式切换对部件退化过程的影响,进行长期累积角度下的寿命预测模型是部件级剩余使用寿命预测的一个挑战。其次,由于模式、环境等因素的影响,部件监测数据特征在全生命周期并非遵循统一变化规律,可能具有短期波动、短期循环、长期指数、长期线性等多种叠加的变化趋势。普遍而言,系统通常呈前期缓慢、后期加速的退化趋势。因此,针对部件短期数据展开研究,进行局部老化预测是剩余使用寿命预测研究的另一个挑战。
为了解决以上问题,提出一种新型的混合模型寿命预测方法,从长期和短期两个不同的时间尺度分别提取相应的老化特征,建立两种不同功能的机器学习模型,分别获得均衡风缸控制系统的长期和短期寿命预测结果,并对两者进行融合,实现剩余使用寿命的实时预测。本文创新点如下:
(1)分析制动机均衡风缸控制系统的工作原理和老化机制,建立系统关键老化部件的数学模型,基于电空阀驱动电流提取能表征部件健康状态的静态指标。
(2)挖掘隐藏在工作模式动态变化中的老化信息,构建部件累积物理动态指标,并基于长期累积特性建立循环神经网络预测模型。
(3)应用短期时间滑窗提取特征序列的频域能量特征和时域统计特征,建立改进的轻量梯度提升机获得短期序列的预测结果。
(4)通过分段模型平均方法将长期和短期的寿命预测结果进行融合,复原搭建DK-2均衡风缸控制系统实验平台,验证健康状态评估结果。
1 均衡风缸控制系统结构与静态健康指标
1.1 均衡风缸控制系统结构与老化特点
均衡风缸控制系统主要由缓解电空阀、制动电空阀、均衡风缸、重联电空阀等组成[19],如图1所示。其工作过程可以描述为:控制单元依据手柄位置设定对应的均衡风缸目标气压,协同均衡EP控制模块、多功能电空阀、气压传感器、PWM脉宽调制策略实现对均衡风缸压力的闭环控制,通过中继阀进行列车管的充排风,使列车管的压力与均衡风缸压力保持同步[20]。
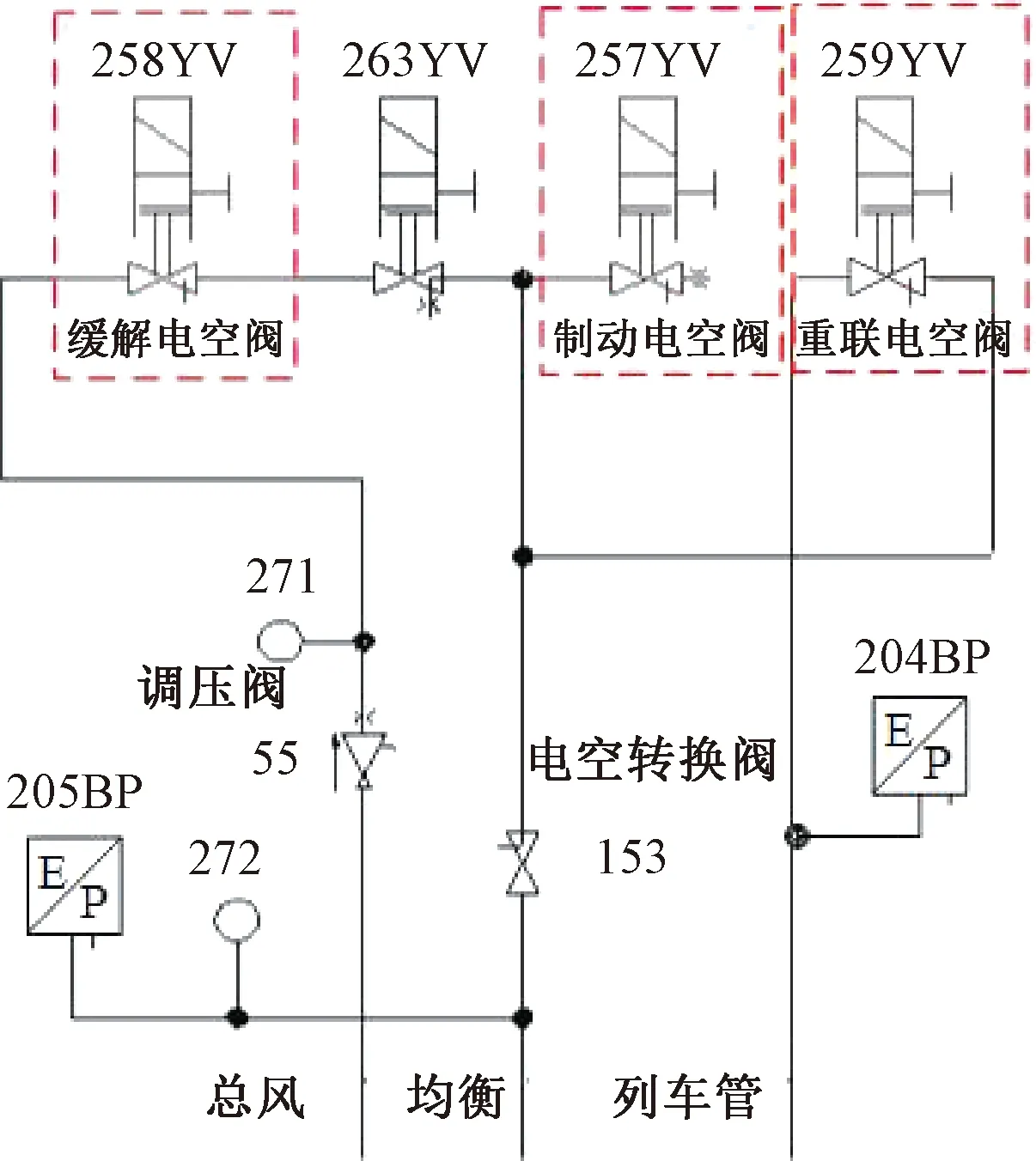
图1 DK-2制动机均衡风缸控制系统
均衡风缸控制系统主要工作于6种模式,即自动制动、自动缓解、紧急制动、紧急缓解、重联和快速缓解模式[21]。均衡风缸压力有3种目标值500、360、0 kPa,其中目标压力由高到低转换实现列车制动,由低到高转换实现列车制动缓解。具体工作模式及目标压力变化和主要动作部件见表1。
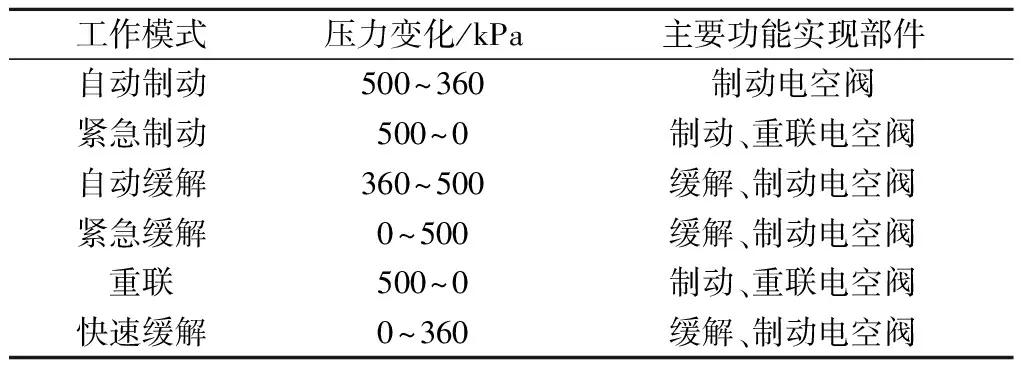
表1 均衡风缸控制系统主要工作模式
由表1可知,各模式下频繁动作的关键部件包括制动电空阀、缓解电空阀与重联电空阀,且不同的工作模式需要不同种类及数量的电空阀配合完成。然而实际制动系统的工作模式发生的频率并不相同,对应着不同的电空阀使用频率,导致各部件的剩余使用寿命处于不同的水平,使整个系统表现出复杂的长期老化趋势[22]。
此外,部件在不同的老化状态承受损伤的能力不同,如电空阀在健康状态动作多次弹簧也不会发生断裂,但在老化后期、弹簧已经产生裂纹时,可能多动作一次弹簧就会彻底断裂,因此系统老化在全寿命后期具有突发性和短期性。
综上所述,本文以电空阀为研究对象,从长期和短期两个方面评估均衡风缸的健康状态。长期角度考虑工作模式切换对电空阀退化趋势带来的影响,短期角度考虑短期循环、短期波动等多种因素叠加造成的老化影响。
1.2 电空阀模型及静态指标提取
1.2.1 电空阀数学模型
电空制动机均衡风缸控制系统中,重联电空阀采用MAC250B-761JA型号电磁阀,制动电空阀与缓解电空阀均采用MAC130B-611JA型号电磁阀。根据电气原理可对电空阀进行简化,建立统一的电空阀数学模型[23],如图2所示。
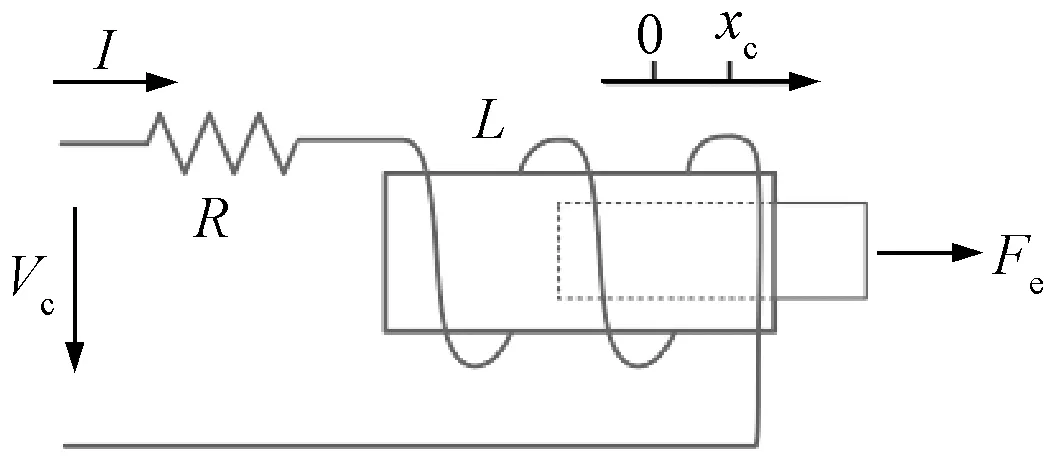
图2 电空阀电磁原理简化示意
当电空阀上电时,线圈磁场与电枢共同作用产生推力,通过阀杆改变气路联通状态;掉电时,线圈释放电感能量,复位弹簧产生弹力推动阀杆回位,气路状态改变,可表示为微分方程中出现的附加项I·dL(xc)/dtc,电路方程为
( 1 )
式中:xc为阀芯位移;I为线圈电流;Vc为端电压;R为电阻;L为线圈电感;tc为时间。对阀芯运动过程进行受力分析,得到电磁力方程为
( 2 )
( 3 )
式中:Fe为电磁力;Cv为阀芯动摩擦因数;kc为弹簧系数;mc为阀芯质量;Cf为黏滞性阻尼系数。
1.2.2 电空阀静态指标提取
基于以上电空阀模型分析,可知电、磁、力之间的协同作用促使阀芯动作,阀内部件老化通常伴随着此3种元素中的某一种或多种影响,导致阀体发生变化。3种元素的相互耦合导致难以针对每一种因素提取出对应的静态指标。
目前制动机对均衡风缸控制系统的可监测信号主要有电空阀驱动电压、驱动电流和风缸压力。其中驱动电压在电空阀老化全寿命周期内基本保持不变,很难从中提取老化特征;而风缸压力的变化较为缓慢,且受到压力传感器精度影响,不适合作为电空阀的老化指标。另一方面,基于其他种类监测信号的健康状态评估方法,如加装加速度传感器监测振动信号,或者霍尔传感器监测磁场强度等,此类方法的稳定性容易受机车运行环境、车身振动与磁场变化的影响,同时加装传感器成本相对较高。
相比上述各种指标,驱动电流在有效性、稳定性、实用性方面都更具有优势,并已经有了研究基础[24]。选取电空阀的驱动电流来解释部件老化过程,考虑工作模式切换、动态波动等因素,从长期和短期两个时间尺度,时域和频域两种角度提取混合老化特征,实现均衡风缸系统健康状态的准确评估。
电空阀正常工作时的驱动端电流变化如图3所示,工作过程主要包括吸合触动阶段(0—A)、吸合运动阶段(A—B)与通电保持阶段(C)。
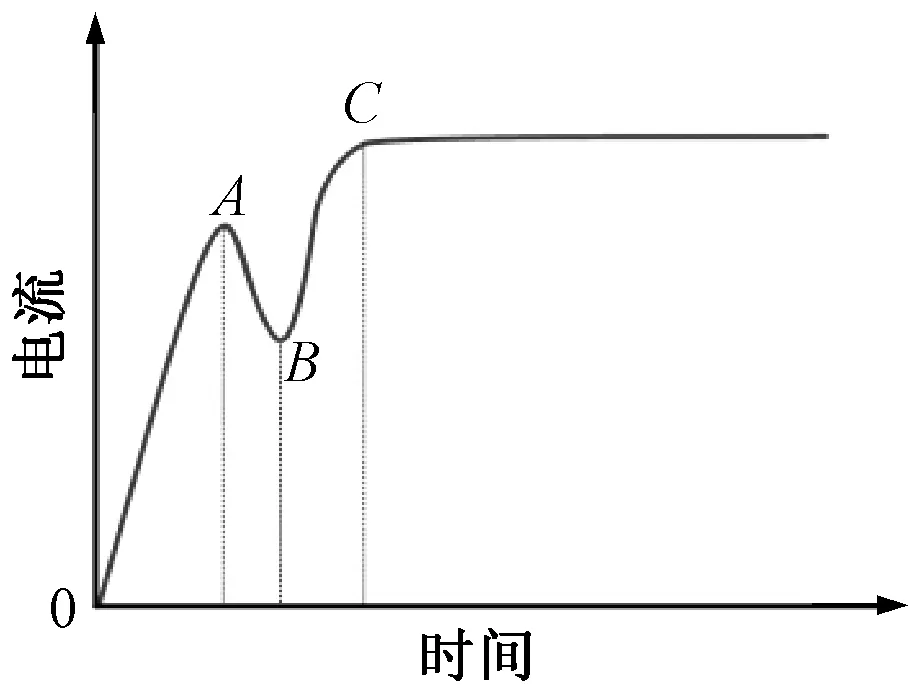
图3 电空阀驱动端电流波形示意
在电空阀通电时,驱动端采集的电流逐渐增加,但此时线圈产生磁力仍小于阀芯受到的阻力,阀芯并未运动,整体处于吸合触动阶段,令L1表示线圈初始电感,此时电路方程可表示为
( 4 )
式中:Vc与L1为常数;I单调变化。
电流升高至A点时,磁力逐渐大于阀芯受到的阻力,阀芯开始运动,磁路气隙发生变化,同时线圈产生与激励电压方向相反的感应电动势,电空阀处于吸合运动阶段。阀芯逐渐动作至最大位移时(即B点),阀芯停止运动。
在电空阀的整个动作过程中,采集驱动电流并提取相应的静态特征G。具体如下:提取0时刻到A点的时间间隔(吸合触动阶段)为特征G1;提取拐点A的电流值作为特征G2;提取A点到B点的时间间隔(吸合运动阶段)作为特征G3;提取拐点B的电流值作为特征G4;提取B点到C点的时间间隔(通电保持阶段)作为特征G5,提取C点后的电流值作为特征G6。
2 结合长期和短期寿命预测的健康状态评估
2.1 基于累积特征的长期寿命预测
电空阀在不同工作模式下的状态不同,退化程度受到的影响也不同,因此,处于模式切换工作状态下的部件老化过程更为复杂。部件的老化是一个累积、缓慢的过程,其当前的退化程度是由其历史经历决定的,换而言之,当前的寿命水平与长期累积的工作经历有很大关联,本节从长期角度建立累积老化预测模型对部件进行基于长期序列的剩余使用寿命预测。
2.1.1 部件累积物理动态指标提取
设均衡风缸系统采集到的部件监测数据集为S,对N个部件进行数据监测,每个部件对应的静态特征个数为k,系统工作于M种工作模式,构建累积物理动态指标F=(F1,F2,F3,F4)。其中:
(1)F1为平滑特征,原始电流信号通常包含噪声因素,为了使长期变化更为明显,滤除短期波动,使用平滑算法对静态指标序列进行滤波处理,获得平滑特征,其维度与传感器维度k相同。
(2)F2为各模式的累积动作次数,部件工作在不同的模式下受到的损伤不同,提取部件在每次动作时已经经历过的各模式的累积动作次数作为特征,其维度与模式种类数M相同。
(3)F3通过计算当前动作与各模式上次动作的时间间隔得到,表示为各模式动作序列号的前向差值,其维度与模式种类数M相同。
(4)F4通过计算当前动作与各模式上次动作对应的静态指标间的差值获得,表现为各模式的静态指标的前向差值,其维度等于k·M。
累积物理动态指标提取过程如图4所示,图4设置6种工作模式,显示长度为40的一维特征变化平滑曲线,模式1至模式6分别对应表1中的紧急缓解、自动制动、重联、快速缓解、自动缓解、紧急制动。图4重点标注了第25次动作的数据点(红色圆圈)进行累积指标提取,该点对应的纵坐标值为F1特征;相同模式动作序列(红色方框)的累积动作次数为F2特征;差值对比点用黑色圆圈标注,次数差值(蓝色线段)为F3特征,数值差值(绿色线段)为F4特征。
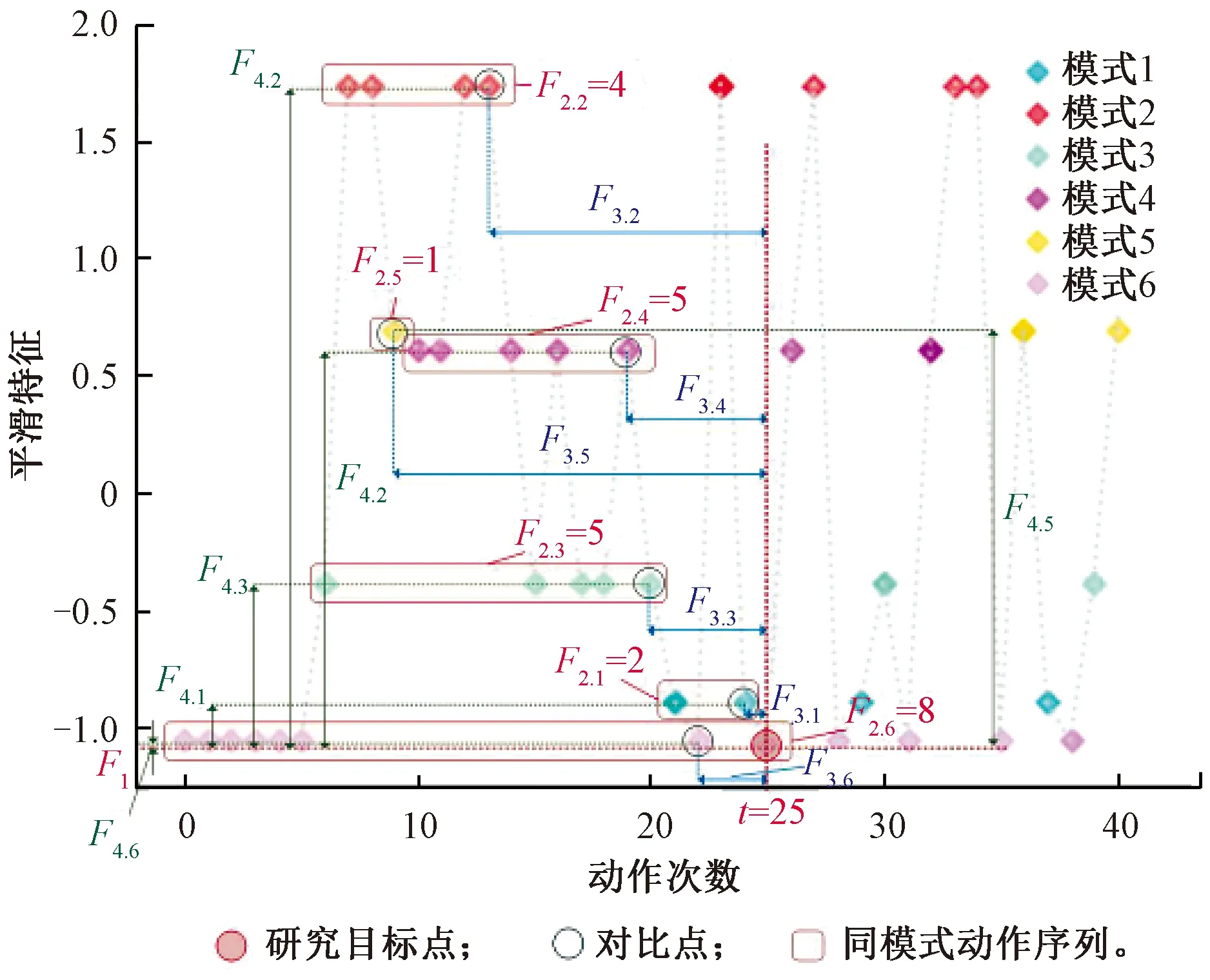
图4 部件累积物理动态指标提取过程示意
2.1.2 基于门限循环单元神经网络的部件长期累积老化预测
通过上述可获得目标部件,即缓解电空阀、制动电空阀与重联电空阀的累积物理动态指标,通过构建门控循环单元神经网络模型学习各部件的累积物理动态指标与剩余使用寿命之间的关联关系。设部件静态指标维度为k,将其与模式切换序列转换为累积物理动态指标作为模型输入,进行部件的累积退化评估。
x(t)为预测模型输入的累积物理动态指标序列,y(t)为健康状态输出序列。门控循环单元以当前输入x(t)、上一时刻输出h(t-1)为输入,通过更新门和重置门完成数据运算,输出当前预测结果h(t)。更新门更新当前状态为
u(t)=σ(Wux(t)+Vuh(t-1)+bu)
( 5 )
式中:Wu、Vu为权重矩阵;bu为偏置量。三者之和通过σ(sigmod激活函数)将结果缩放至0~1范围内,结果接近于1说明上一时刻的信息保留程度接近完整。同样,重置门使用参数Wa、Va和ba进行数据计算,确定上一时刻的信息中需要遗忘的程度,该值越接近0,遗忘程度越趋于全部。
a(t)=σ(Wax(t)+Vah(t-1)+ba)
( 6 )
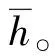

( 7 )
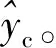
2.2 基于局部特征的短期寿命预测
数据静态指标在整个生命周期变化规律并不统一,在长期与短期通常具有不同的变化趋势。为了针对部件的老化数据进行基于短期序列的退化评估,通过使用滚动时间窗将部件静态指标序列进行分割得到碎片数据集,定义时间窗口大小为Lw。为获得更多短期序列样本,使用滚动时间窗进行可重叠的序列切割,并根据短期序列中最后一次动作对应的剩余使用寿命对序列样本打标签,获得窗内短期序列样本集s。
2.2.1 基于碎片数据集的局部特征提取
短期序列数据可体现一定时间范围内数据的波动程度,在时域范围内可获得数据的统计特性以及变化波动程度,数据在频率层面的变化可反映部件物理性质的变化,可将分离出的不同频率波段的信号转换为能量特征进行表示。
(1)时域特征提取:本文提取3种时域统计特征表示短期内静态指标变化,针对每个窗内样本进行时域特征v=[v1,v2,v3],其中,局部序列平均值v1反映窗内序列样本的集中趋势;局部序列方差v2反映窗内序列样本的波动趋势与离散程度;局部序列偏度v3反映窗内序列样本分布偏斜方向和程度,是序列数据分布非对称程度的数字特征,表示为三阶标准矩。时域特征为
( 8 )
(2)频域特征提取:针对部件的短期序列样本进行频域波动分析并提取能量特征。
针对目标序列在时频空间中添加均匀分布的高斯白噪声,以改变序列整体的极值点分布,补足了信号间歇处的不足。向时间窗内序列数据s(t)添加Ng次均值为零、幅值为αnoise的白噪声g(t),即
( 9 )
参数Ng和αnoise的选值由下式确定
(10)
式中:wg为权重系数;μ1为序列标准差。根据经验通常取wg=0.2μ1。

(11)

(12)
最终得到的每个IMF分量表示一个不同频段的平稳信号,其能量变化可以反映系统的老化信息。IMF分量的能量熵e=[e1,e2,…,ez,…,eZ]作为部件的局部老化频域特征。
(13)
2.2.2 基于改进的轻量梯度提升机的部件短期局部老化预测
获得部件的短期局部特征后,构建改进的轻量梯度提升机模型进行短期角度的部件剩余使用寿命预测。轻量梯度提升机算法以梯度提升决策树作为模型构建基础,通过使用串行集成策略,集成多棵回归树并进行结果的累加从而避免过拟合问题,实现轻量级、更低计算复杂度的数据预测,基于此模型进一步改进实现部件短期退化性能评估,具体流程如图5所示。
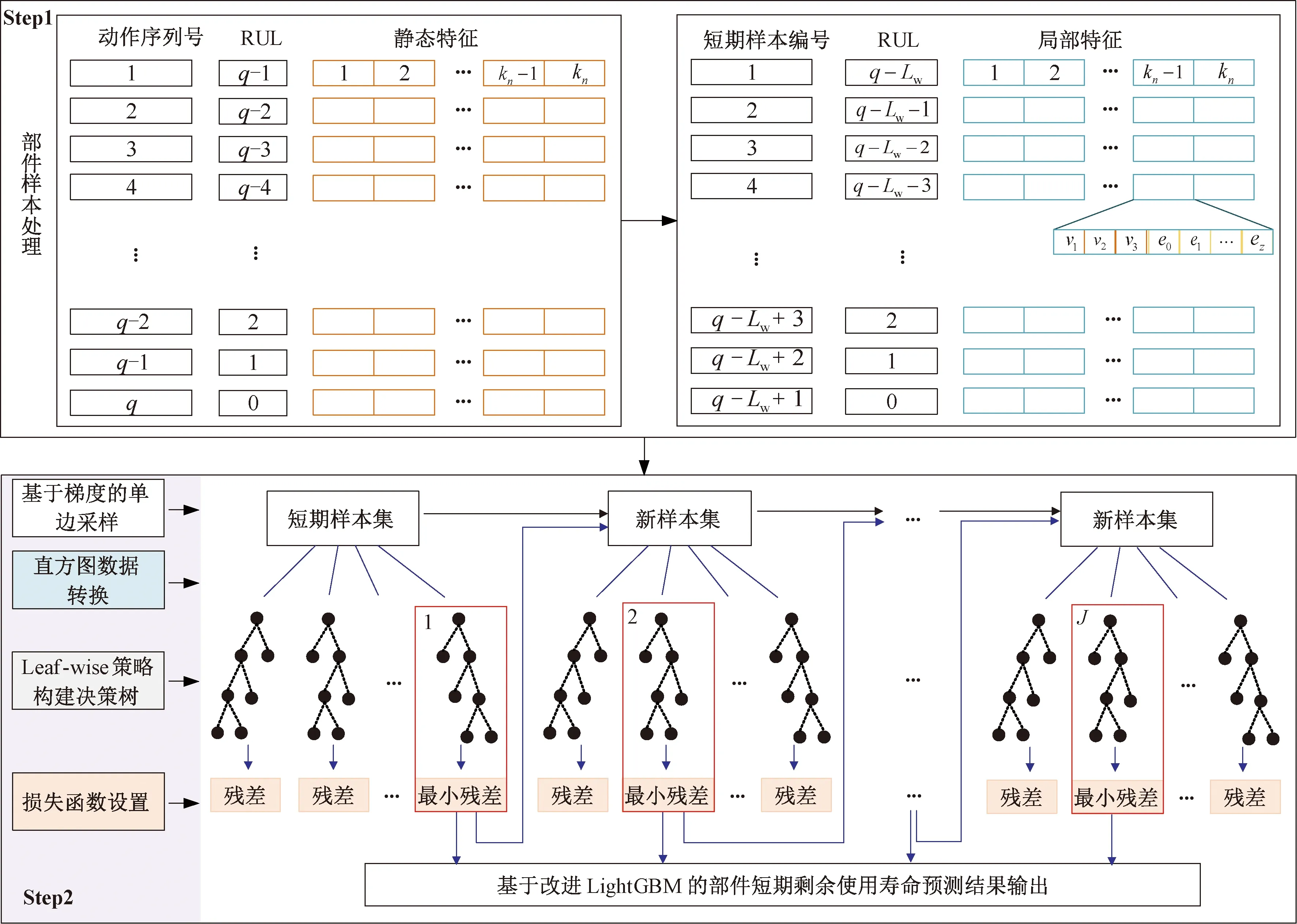
图5 基于改进的LightGBM部件级短期局部剩余使用寿命预测流程
为便于理解,图5剩余使用寿命(RUL)标记为剩余使用次数,q为原始样本的生命周期长度,使用时间窗内最后一次动作对应的健康状态值作为该短期样本的使用寿命,短期样本对应k维局部特征,每一维局部特征包含对应静态特征的时频域特征。针对所有原始样本进行Step1处理得到短期样本集。

(14)
(15)
(16)
式中:μ为叶子数量U的惩罚参数;ωu为每个叶子的权重;τ为惩罚参数。令Stree表示包含所有树的空间,通过添加所有决策树的预测结果获得最终的预测模型输出为
(17)
本模型的重要研究策略与改进包括以下几点:
(1)考虑梯度较大的部件样本在计算信息增益中起着更为重要的作用,采用基于梯度的单侧抽样策略对数据进行分割,针对梯度较小的样本进行随机采样以提高算法效率。
(2)使用直方图算法将部件样本数据离散化以寻找最优分裂点,可以实现更低的内存占用率与计算复杂度。
(3)构建决策树时使用Leaf-wise生长策略,针对每层选择分裂增益最大的节点进行继续分裂构建树,不再针对同层的其他节点进行研究,可避免消耗不必要的计算资源。
(4)考虑部件复杂的工作环境会提高样本的多样性,易引起预测过拟合问题。定义当预测剩余使用寿命大于真实值表示进行了早期预测,小于则说明为晚期预测,早期预测比晚期预测会造成更严重的后果。为此,本模型改进了轻量梯度提升机的损失函数。一方面引入正则项以弱化过拟合的可能,另一方面对晚期预测样本赋予更高的权重,使其在训练时获得更大的梯度、更受重视,以减少早期预测的可能。

2.3 基于分段模型平均的剩余使用寿命预测结果融合
目前常用融合策略包括装袋法,集成法、滤波法等,其中装袋法与集成法需要花费较多的计算时间,滤波法如卡尔曼滤波算法在实际应用时需要知道真实的剩余使用寿命,而此点通常难以保证。针对本文情况,已经获得的基于长期、短期的剩余使用寿命预测结果理论上已经具有较高准确程度,可以使用简单的模型平均法即可实现预测结果的融合。
(18)
考虑不同部件在不同寿命对长期、短期的寿命预测结果有着不同的偏重,通过设置健康状态阈值,对决策结果进行分段融合
(19)
式中:θγ为分段阈值;γ1、γ2为权重参数。总体实现了基于长短期混合模型的部件级剩余使用寿命预测,通过联合长期累积预测模型与短期局部预测模型的预测结果获得最终的部件剩余使用寿命。
本章构建的整体模型具体应用于制动电空阀、缓解电空阀与重联电空阀的剩余使用寿命预测问题,下文将使用实际电空阀数据对提出的部件级剩余使用寿命预测模型进行加速老化实验和仿真验证与分析。
3 实验仿真验证与结果分析
以DK-2制动机均衡风缸控制系统为模板,在实验室复原搭建了系统电气路实验平台。平台整体的能量由电源模块供给;制动控制单元是DK-2制动机的核心控制部分,用以进行列车制动控制、制动机模拟量及通信数据的实时处理,根据工作指令对均衡系统电空阀进行PWM控制,并通过压力反馈进行调整;数据采集模块用于采集电流数据、压力数据并将数据暂时存储。
电流采集模块使用USB-4222型号采集系统,该系统提供16个具有独立A/D转换单元的模拟输入通道,各通道采集的数据在时间上保持同步,最高采样率为250 kSa/s,分辨率为12 bit,FIFO缓存区大小为16 kB采样点,USB接口规范为USB 2.0高速接口。压力数据可直接通过制动控制单元进行采集,并可以通过TCP/IP协议实现数据传输。
具体实验步骤为:螺杆式空压机产生750~950 kPa的压缩空气,经过干燥器、油水分离器后存储在100 L的总风缸中,空气进入均衡系统,系统中部件根据功能要求调整工作状态,空气由此进入均衡风缸、列车管或排至大气,通过充风、排风改变缸类组件的气压值,完成均衡风缸控制系统控制的最终目标。由于平台限制,考虑需要获取的是列车管的压力数据,本平台使用风缸进行列车管模拟以获得压力数据。
3.1 实验设置与监测数据获取
均衡风缸控制系统实验平台工作于多模式切换的条件下,使用PWM控制电空阀。其中,制动电空阀与缓解电空阀为MAC130B-611JA型号电空阀,实验设计动作周期为40 ms,占空比为4∶1,前32 ms得电,后8 ms失电;重联电空阀为MAC250B-761JA型号电空阀,实验设计动作周期为240 ms,占空比为5∶1,即前200 ms得电,后40 ms失电。设置加速老化实验采集电空阀数据,系统每隔2 min采集一次电空阀数据,数据记录长度为10 s。
为获得系统老化数据,令均衡风缸控制系统工作于多模式切换状态,具体包括500~0 kPa、360~500 kPa、0~500 kPa、500~360 kPa、360~0 kPa、0~360 kPa 6种模式,持续工作直至系统不满足DK-2制动机技术指标视为系统故障,停止采集。为了保证机器学习模型的泛化能力,选取重联电空阀、制动电空阀、缓解电空阀各20个,共60组样本进行仿真分析和结果验证,其中80%的样本用于训练,20%样本用于验证,每组样本的电空阀动作次数至少达到百万次,由于部件的工作次数量级庞大,紧邻的两次动作电流曲线变化程度不大,故此根据记录数据每隔1 000次抽取一次动作的数据进行仿真实验。
3.2 预测模型评价指标设置
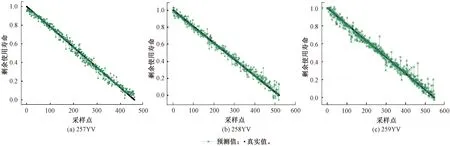
在仿真结果分析中,电空阀的健康状态yt定义为剩余使用次数占整个生命周期的百分比。y′(t)和y(t)分别表示预测结果和实际结果。如果y′(t)>y(t)说明预测性能偏向早期预测。如果y′(t) (20) PScores=∑PScore(t) (21) 进行短期预测时,使用滚动时间窗对提取的静态指标序列切割并提取局部特征,包括时域统计特征与频域能量特征,时间窗的大小设置会影响短期模型的预测效果。图6为对制动电空阀(257YV)、缓解电空阀(258YV)和重联电空阀(259YV)使用不同时间窗长度进行序列分割,构建的短期剩余使用寿命预测模型的性能评价指标值变化过程。 图6 部件不同时间窗长度下的评价指标值对比图 实验采集的电流曲线标记电空阀的全剩余使用寿命序列,并从数据中提取3种阀的电流静态特征。短期预测时,从图6中遍历选择最优的时间窗长度分别为60、70、90。改进的LightGBM模型的提升类型选择GBDT,叶子节点数为100,建树的样本采样比例为0.8,建树特征选取比例为0.7。 图7为制动电空阀(257YV)、缓解电空阀(258YV)和重联电空阀(259YV)样本短期局部的健康状态预测结果,由于不同样本的生命周期长度不同且采样点过多,为更清晰观察预测效果,等间距分别抽取450、520、540个点绘制预测结果示意图。由图7可知,在部件老化末期,短期局部预测模型的预测结果更准确,且相较于早期预测,整体预测波动更倾向于晚期预期。 图7 基于短期局部特性的剩余使用寿命的长期预测结果 在基于长期累积特性进行剩余使用寿命预测时,其预测结果如图8所示。分析预测结果发现,部件老化初期的长期剩余使用寿命预测结果通常偏离较小,这是因为在部件老化初期,其物理性质并没有较大改变,因此长期累计预测获得了较好的预测效果。对比图7与图8,可以看出长期预测结果与短期预测结果具有互补性,长期预期在老化前期预测准确度更好,而短期预测在老化末期预测准确度更好。 使用分段模型平均法融合长期与短期剩余使用寿命预测结果,针对制动电空阀(257YV)、缓解电空阀(258YV)和重联电空阀(259YV),阈值θγ分别设为0.52、0.62、0.34;权重γ1分别设为0.22、0.12、0.41;权重γ2分别设为0.73、0.51、0.62,参数选择时,以Scores指标作为选择依据进行遍历搜索,融合后的剩余使用寿命预测结果如图9所示。 对比基于长短期的预测结果,可以看出融合后的预测模型综合了长期与短期两种预测模型的优点,实现了在部件老化初期、末期都具有良好的预测性能。此外,分别使用RMSE与Scores两个评价指标,对长期预测模型、短期预测模型、长-短期混合模型在整个数据集上的预测性能进行评价,为增加模型对比的全面性,分别使用循环神经网络(RNN)、支持向量回归(SVR)、卷积神经网络(CNN)、堆叠自编码器算法(SAEs)进行部件剩余使用寿命预测。 RNN算法具有神经元跨时间自连接的网络结构,可以很好的处理各种时间序列相关问题,是经典的时间序列预测类模型;SVR算法通过寻找最优超平面进行数据预测,是应用范围最广的浅层学习模型;CNN算法通过卷积核形成多个特征映射,具有一定的特征挖掘功能;SAEs算法可以对原始数据进行多种表达学习。将上述模型与本文提出的剩余使用寿命预测模型进行预测性能对比,不同模型的评价指标值对比见表2。 表2 不同模型下部件健康状态预测性能评价 对比评价指标值可发现,模型对制动电空阀与缓解电空阀的预测效果要优于重联电空阀,这是因为由于电空阀型号不同,导致采集的数据变化趋势不同,从波形示例图中也可以看出重联电空阀的驱动端电流波动更大,噪声更多,数据的质量对预测效果有很大影响。 此外,单独选择长期累积预测模型、短期局部预测模型进行使用寿命的预测也具有较好的预测性能。具体而言,预测性能分别在部件老化前期与末期具有不同的偏重。由于两个预测模型性能具有较好的互补性,融合后可以获得更好的预测结果,具体表现为本文提出的结合长期短期特征混合模型的剩余使用寿命预测模型相比较而言具有最低的RMSE与Scores评价值,验证了提出模型的有效性。 本文针对DK-2制动机均衡风缸控制系统多模式切换工作状态下的健康状态评估问题展开研究。将剩余使用寿命作为健康状态评估的依据。首先对均衡风缸控制系统部件级剩余使用寿命预测问题展开描述,设计结合长期和短期特征的混合模型对剩余使用寿命进行预测。通过分析部件的失效机理,提取反映部件状态的物理指标;在此基础上,分别构建基于累积动态物理指标的长期剩余使用寿命预测模型与基于局部特征的短期剩余使用寿命预测模型;最后利用分段模型平均方法进行不同模型的预测结果融合,再将其转化为健康评估指标。通过搭建实验平台,获得DK-2制动机均衡风缸控制系统制动电空阀、缓解电空阀与重联电空阀的真实老化数据,利用平台数据对所提方法的有效性进行了仿真验证。
3.3 实验仿真与预测结果分析


4 结论

