基于盲孔法的钢绞线有效预应力检测识别技术

张志国，吴冀桥，张彩亮，许 琪，陈叶鑫，王泽远

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043；3.武汉江腾铁路工程有限责任公司，湖北 武汉 430063；4.中国铁道科学研究院，北京 100081)

近年来,预应力结构广泛应用于桥梁、岩土等工程领域,有效预应力大小是衡量在役预应力结构工作性能的重要指标。钢绞线作为铁路预应力混凝土梁桥中预应力的主要载体,准确识别其有效预应力是在役铁路桥梁安全性评判的重要内容,可降低结构因预应力失效而造成的梁体开裂甚至坍塌事故风险[1]。另外,国内诸如大秦铁路、朔黄铁路等面临重载改造,铁路桥梁中预应力钢绞线有效预应力大小的识别对改造工程也有重要参考作用[2]。刘永前等[3]对朔黄铁路等重载铁路常用预应力混凝土简支T梁梁端斜裂缝的产生机理进行了数值模拟及试验研究,发现梁端最大主拉应力及剪应力随梁体预应力损失的增大而增加,尤其在梁端截面中性轴附近位置处的最大剪应力增幅极为明显,是梁端斜裂缝产生的重要因素。薛继连[4]通过对朔黄铁路39座桥涵结构进行原位试验,以及对更换下来的32 m普通高度预应力混凝土简支梁进行静载开裂试验,分析不同跨度及截面高度桥梁在大轴重载下的结构响应,并提出采用预应力碳纤维板加固梁体来提高其抗裂性能。目前,国内外识别钢绞线有效应力的方法众多,按照检测方法特性可分为直接检测和间接检测,直接检测法是利用检测仪器直接拾取钢绞线的位移、电磁、声、波等物理信号,通过这些物理信号和钢绞线有效预应力建立起对应关系,由此直接得到钢绞线有效预应力的大小,常见的直接检测方法有拉脱法、横张增量法、振动法、波动法、电磁检测法、超声导波法、切割法等,这类方法存在较苛刻的使用条件,精度受测试过程影响较大、理论基础尚不完善,有的方法还会对结构造成较大二次损伤等问题,导致难以在既有预应力混凝土梁桥结构有效预应力检测中得以广泛推广。间接检测方法常见于预应力混凝土梁的有效预应力识别,建立有效预应力和梁体结构力学特性之间的关系,通过一定手段检测混凝土梁的性能再反算出钢绞线有效预应力大小,常见的间接检测方法有:局部应力释放法、消压弯矩法、动力测试法、等效质量法等[5]。由于混凝土材料本身的复杂性能特征,以及其性能还会随时间产生徐变和劣化,加之预应力多束配置的相互影响,通过性能检测再间接反推预应力的方法本身存在着先天不足,不可避免地会造成较大离散性和系统误差,实际测试精度如何保证尚需进一步展开研究。另外,间接法还需要施加较大的载荷试验,这在实际工程中,尤其对已存病害的桥梁实施具有较大的安全风险隐患,甚至是无法实现的。

综上所述,尽管针对钢绞线有效预应力已经探索了很多不同的检测方法,但尚未形成一种公认的有效方法。鉴于当前国内外还没有一种简单有效、普适性强、精准可靠的钢绞线有效预应力检测方法,本文在已有研究基础上,提出采用盲孔法识别钢绞线有效预应力的方法,以期在检测精度和对梁体局部破损之间寻找平衡点,建立一种新型的局部损伤检测方法。这种局部损伤不至于对桥梁性能造成影响,而且可根据现行规范进行修补恢复。

盲孔法属于局部应力释放法中的一种,目前国内外对应力释放法已有系列研究。1934年,Mathar[6]首次提出通过测量构件钻孔后孔边应变来确定金属构件的残余应力,后由Soete等[7]发展完善而形成较系统的理论方法。经过多年发展,逐渐形成了盲孔法、钻孔法、环孔法、剥层法、开槽法等多种对金属构件进行应力释放及残余应力识别的方法。Mainjot等[8]提出采用积分法来检测不均匀残余应力场的残余应力,扩大了盲孔法检测金属残余应力的适用范围。

盲孔法从早期的检测金属构件残余应力发展到现在的预应力混凝土构件检测。1999年,杨勇等[9]提出了使用应力释放法计算预应力混凝土梁预应力损失值的思路,并运用该法对某预应力T形刚构桥进行有效预应力检测。2003年,戴福隆等[10]提出用云纹干涉法测量位移信息代替应变片测量应变信息来确定钻孔法的孔周残余应力,得到了钻孔释放的位移与残余应力的关系。2009年,刘玲晶[11]对一片3 m长预应力混凝土梁进行了环孔法试验研究,分析了钢束位置对测点应力释放值的影响,并给出了估算现存预应力的经验公式。2010年,英国学者Schajer[12]分析总结了钻孔法这些年取得的进展,并指出在有着先进温度控制、振动隔绝的实验室中利用光纤技术测量钻孔表面微量位移将成为有效预应力检测未来的发展方向。2012年,周晶[13]使用有限元软件对预应力混凝土小箱梁进行建模,在箱梁跨中底板进行钻孔,分析了改变孔深、孔径时孔周边的应力分布情况以及对应力集中系数的影响。2014年,刘志勇[14]以既有铁路简支T梁为研究对象,采用开槽法、消压弯矩法以及结合理论计算对试验梁的预应力损失进行了识别,证实了开槽法在实际工程中具有一定可行性。2015年,Blödorn等[15]提出盲孔法钻孔时若没有适当控制时,可能在孔壁中引入额外的应力,继而影响盲孔法测量的准确性。2018年,毛硕[16]通过对一片预应力混凝土T梁进行ANSYS有限元建模模拟和现场试验相互印证的方法得出,开槽法试验应力释放至零的切割深度与两条平行槽间距之比为0.32～0.34,且数值模拟了相同尺寸的环孔、方孔、平行槽的应力释放为零的开槽深度,发现开槽深度与开槽的方式基本无关。2019年,Lee等[17]提出一种基于应力释放法(SRM)和数字图像相关法(DIC)相结合的混凝土结构静态应力估算方法。与应变计的逐点测量相比,DIC获得的全场位移数据量更大,估算结果精度更高。2020年,马腾[18]对联合加载应力释放过程进行了研究,发现通过施加一定大小的荷载消压,可以减小开槽法应力释放的深度,工程上可以利用这一点减小开槽法检测有效预应力时对梁体的损伤。

本文在金属构件及混凝土应力释放法现有研究基础上,提出在钢绞线上钻盲孔来识别钢绞线有效预应力的方法,通过ANSYS有限元软件对预应力混凝土常用七丝钢绞线钻孔过程进行仿真计算来探索钢绞线钢丝钻孔后孔边应力释放规律,并对影响应力释放过程的钻孔参数进行影响规律分析,以获取合适的钻孔参数,来指导钢绞线实际钻孔试验,并验证钻孔应力释放规律的正确性及钻孔参数的合理性;同时,据试验结果建立钻孔后孔边应变释放量与钢绞线有效预应力之间的函数关系,并对其误差及其适用性进行分析。

1 基本假定与盲孔法基本原理

基于盲孔法识别预应力钢绞线,主要遵循以下基本假定:

(1)线弹性假定。钢绞线在钻孔过程中除钻孔位置外,其周边材料仍处于弹性受力状态,各根钢丝均处于弹性工作阶段。

(2)均匀性假定。钢绞线张拉后,远离边界条件的区域,外围钢丝的应力状态基本相同。

(3)单向应力状态假定。钢绞线钢丝受拉后近似处于沿轴向单向受拉应力状态。应力释放过程中假定各钢丝之间接触面摩擦系数保持不变。

本文盲孔法是借鉴在混凝土表面开槽、钻孔等应力释放识别法以及钢板表面钻孔反算残余应力方法基础上,考虑钢绞线本身结构组成及受力特征,把张拉后钢绞线各组成钢丝近似看作处于轴向受拉的单向应力状态,通过采用专用合金钻头在钢丝直径上钻某一深度、一定直径的盲孔后,测得孔边释放应变,由此反算出钢丝有效应力,进而得到整根钢绞线有效应力的一种方法。该法的核心是建立钻孔释放应变和钢绞线有效预应力之间的关系,具体实施时,可以将仿真模拟和试验验证相结合,建立反映二者之间关系的拟合公式,然后随工程应用数据积累不断完善。

2 钢绞线钻孔精细化分析模型

本文采用ANSYS软件进行仿真计算,模型采用8节点Solid185实体单元建立,将钢绞线纵轴线方向设为z轴,将钻孔方向设为y轴,x轴垂直于z-y轴所构成的平面,见图1。钢绞线两端边界条件为一端固定,一端张拉。七丝钢绞线的建模参数取自规范GB/T 5224—2014《预应力混凝土用钢绞线》[19]与GB/T 5223—2014《预应力混凝土用钢丝》[20],采用1860级钢丝和钢绞线,具体数值见表1。

图1 钢绞线钻孔有限元模型

表1 1×7钢绞线几何及力学参数

本研究主要探讨钢绞线在线弹性阶段张拉钻孔应力释放规律,钢绞线钢丝采用弹性本构模型建模,由于模型是基于钢绞线单根钢丝的精细化建模,故模型弹性模量应以单根钢丝的为准,本文取钢丝弹性模量E=2.05×105MPa。模型长度经过多组仿真结果对比,综合考虑计算精度和计算效率,选取60 mm长度建模。钢绞线之间的接触关系采用面面接触,通过查阅相关文献[21],接触单元选择Targe170和Conta174,建立外围钢丝之间、外围钢丝与中心钢丝之间共计12对接触对,接触面之间的摩擦系数取0.15,考虑标准接触行为,采用系统默认的增广Lagrange乘子法进行接触计算。单元网格划分采用六面体网格,对于要进行钻孔的钢丝,钻孔区域周围网格尺寸采用0.1 mm,孔边应力释放区网格尺寸采用0.2 mm,远离应力释放区网格尺寸采用1 mm,对于不需进行钻孔的中心直钢丝和外围其他5根螺旋钢丝,网格尺寸均采用1 mm,网格划分采用体扫略和体映射相结合方式,见图2。

图2 七丝钢绞线钻孔后网格划分

模型的仿真计算过程为先张拉,后钻孔。最大张拉力按工程施工常用张拉控制应力σcon=0.75fpk=1 395 MPa进行施加,钻孔参数由钻孔半径和钻孔深度确定,将钻孔半径分别取0.50、0.75、1.00、1.25、1.50 mm五种规格,钻孔深度分别取1.0、1.5、2.0、2.5、3.0 mm五种情况,共形成25组不同孔径、钻孔深度的组合工况,为方便实际操作仅考虑在外丝外表面进行钻孔,用符号RaHb表示各组合工况参数,含义为Ra代表钻孔半径和半径大小,Hb代表钻孔深度和深度数值。

3 仿真结果及参数影响分析

3.1 钢绞线钻孔应力释放仿真计算结果

为便于描述仿真试验结果,作如下定义:将钢丝节点距离钻孔左右边缘的z向(钢绞线轴向)距离定义为孔边距;将钻孔前后,钢丝表面孔左右两边节点处的z向应力差值定义为这一节点的应力释放量;某一节点应力释放量与钻孔前应力的比值被称为该节点的应力释放率。

以钢绞线R0.5H1.5工况模型为例展示仿真结果,钻孔前后,钢绞线的z向应力云图见图3。

图3 钻孔前后钢绞线z向应力云图(单位:MPa)

图3(a)、图3(b)显示了钢绞线受拉后的应力云图,由于存在边界条件、钢绞线各丝间复杂接触关系的影响,从整体上看,图3(a)中钢绞线应力分布关系比较复杂,似乎缺少规律性。但在距离边界较远的模型跨中附近,应力云图表现出明显规律性,从跨中截面z向应力云图可以看出,中心钢丝的应力比外围钢丝应力大,且外围钢丝截面应力分布并非均匀,而是分层分布,靠近中心钢丝的内层应力比远离中心钢丝的外层应力大,这一规律与钢绞线各根钢丝间复杂的扭绞接触关系相符合。

图3(c)、图3(d)显示了钢铰线钻孔后的应力云图。钢绞线钻孔后,被钻孔钢丝孔边附近出现应力重分布现象。沿钢绞线轴线方向,孔边拉应力释放为零甚至变为压应力,随孔边距的增加,应力释放量逐渐减小。沿钻孔上下边缘,孔边产生应力集中效应,应力集中系数最大值为2.982,应力集中效应在远离钻孔上下边缘时逐渐削弱。沿钻孔深度方向,在孔深范围内钢丝内部应力分布与表面分布规律相同,未钻通部分由于截面削弱应力增加。

通过ANSYS路径命令,提取出钻孔前后孔左右边缘钢丝表面沿轴线方向5 mm范围内节点的z向应力值,二者相减得到此工况下孔边节点应力释放量,进而求得孔边节点应力释放率,将数据绘制成曲线,见图4。

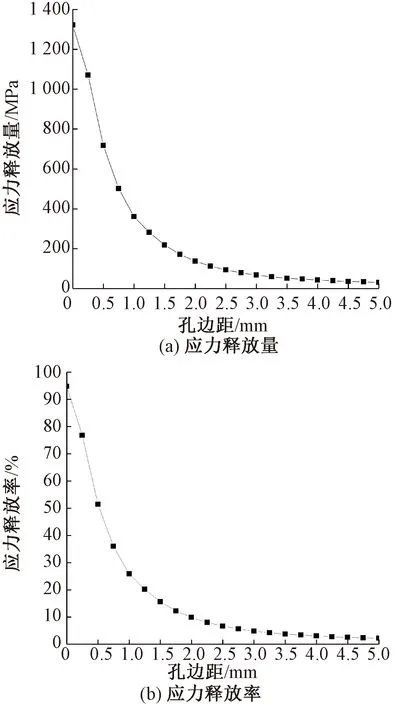
图4 工况R0.5H1.5时钢绞线孔边应力释放规律

从图4可以看出,应力释放量曲线与应力释放率曲线随孔边距的变化趋势相同。随着孔边距增加,应力释放量(率)逐渐下降,且下降趋势由陡峭趋于平缓。从数值上看,在孔边距为0 mm节点处,钻孔后的应力释放量为1 321.9 MPa,应力释放率为98.52%;在孔边距5 mm节点处,钻孔后的应力释放量为30.4 MPa,应力释放率为2.25%。孔边距超过5 mm后,孔边节点应力几乎不受钻孔影响,由此表明钻孔应力释放过程发生在孔边小范围内,远离孔边的钢丝节点应力几乎不受钻孔影响。

3.2 影响钻孔应力释放的参数分析

对钻孔半径分别为0.50、0.75、1.00、1.25、1.50 mm,钻孔深度分别为1.0、1.5、2.0、2.5、3.0 mm,共25种不同工况模型进行钻孔仿真计算,提取出各种工况下钻孔左右边缘5 mm范围内的应力释放量绘制成曲线。

图5为在不同钻孔半径下,钻孔深度对钢绞线孔边应力释放值的影响。

图5 钻孔深度对孔边应力释放量的影响

从图5可以看出,在同一尺寸钻孔半径工况下,孔边同一位置处钢丝应力释放量均随钻孔深度的增加而增加,最终趋近收敛,曲线收敛速度随钻孔半径的增大而减缓。引入深径比(孔深与孔径之比)来表达应力释放曲线的收敛情况,对上述5种不同孔径工况,若相邻两条应力释放曲线上各点的应力释放率差值的平均值k<1.5%,则认为在该钻孔深度下应力释放曲线已经收敛,该工况在此钻孔深径比下已完成孔边应力释放,k的表达式为

( 1 )

经计算可得,当钻孔半径为0.5 mm时,工况R0.5H1.5与R0.5H2.0之间的k=1.3%,孔边应力完成释放的深径比在3.0左右;当钻孔半径为0.75 mm时,工况R0.75H1.5与R0.75H2.0之间的k=0.9%,孔边应力完成释放的深径比在2.0左右;当钻孔半径为1.0 mm时,工况R1.0H2.0与R1.0H2.5之间的k=0.7%,孔边应力完成释放的深径比在2.0左右;当钻孔半径为1.25 mm时,工况R1.25H2.5与R1.25H3.0之间的k=0.4%,孔边应力完成释放的深径比在2.0左右;当钻孔半径为1.5 mm时,在钻孔深度小于等于3.0 mm时,工况R1.5Hb各条相邻两曲线之间的k最小值为1.8%,计算范围内孔边应力释放曲线未达到收敛。

从上述计算结果可以看出,在进行盲孔法钻孔试验时,在孔径取为0.50、0.75、1.00、1.25 mm时,理论上控制深径比在2.0～3.0之间,即可实现钻孔孔边应力的稳定释放。从中不难得出,当所选取钻孔的孔径越大,为完成孔边应力释放所必需的钻孔孔深也要随之增大,对钢丝截面造成的削弱也就越严重,所以在实际进行钻孔释放时,选取钻孔孔径越小越有利。

图6为在不同钻孔深度下,钻孔半径对钢绞线孔边应力释放值的影响。由图6可以看出,在孔边距一定的条件下,钢绞线钢丝应力释放量随钻孔半径的增大而增大,且钻孔越深,钻孔半径对应力释放量的影响越大。越靠近孔边位置,钻孔钢丝应力释放量越大,曲线变化越陡,在一定范围内渐趋平缓。在孔深一定时,随孔径增加,应力释放曲线没有出现收敛态势,但在孔边距超过2 mm后曲线逐渐趋于平缓,所以通过选定钻孔半径再进行合理孔深确定更具合理性。

图6 钻孔半径对孔边应力释放量的影响

根据上述仿真结果,可以得到预应力混凝土梁常用公称直径为15.2 mm七丝钢绞线在利用盲孔法进行有效预应力识别时的钻孔参数。为使钢绞线孔边应力完成稳定释放,且尽量减小钢丝截面受损面积的原则,同时钻孔操作易于实现的要求,取基准钻孔半径0.5 mm,最大钻孔深度可取2.0～3.0 mm,选取外侧钢丝进行钻孔释放试验。

试验时通过应变片测量测点钻孔前后的应变变化,为使测量结果精度更高,应变片的粘贴位置应选择应变释放量值明显,曲线收敛,且应变变化较为平缓的区域。对于试验钻孔参数的选择,结合模拟分析结果将应变片粘贴在孔边距为2 mm处比较合适。

4 盲孔法识别钢绞线有效预应力试验验证

4.1 试验概况

为验证仿真计算得出的钢绞线钻孔后孔边应力释放规律的正确性,以及进一步探索钢绞线有效预应力与孔边应力释放量之间的关系。试验采取的钻孔参数基于仿真计算结果,为进行数据比较,试验时取基准钻孔半径为0.50 mm,对照钻孔半径为0.75 mm共两种钻孔规格,钻孔深度取1.0、1.5、2.0、2.5、3.0 mm五种,测点为钻孔钢丝上距钻孔边缘2 mm处位置以及相邻钢丝与钻孔位置同一截面处。本次试验钢绞线采用天津大强钢铁有限公司生产的1×7-φ15.2-1860级钢绞线,其样品实测参数见表2。

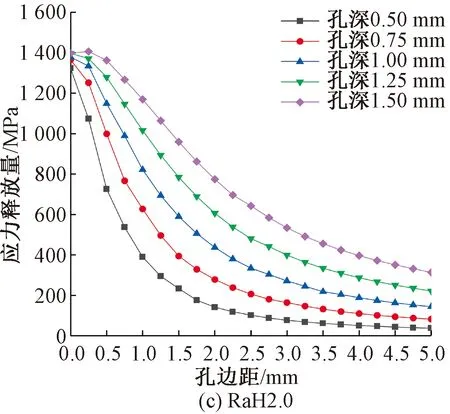
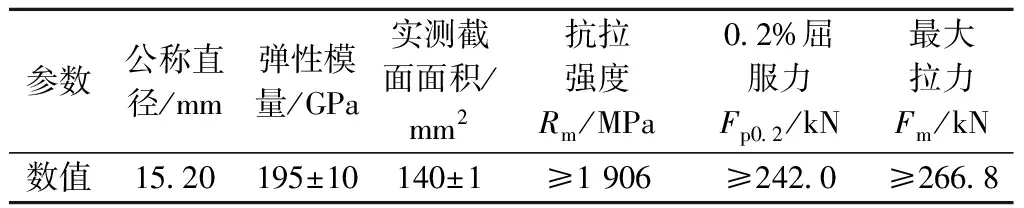
表2 试验用钢绞线参数

本试验采用应变片测量钻孔前后的应变变化,为方便描述,用应变释放量代替仿真计算中应力释放量进行讨论分析。具体试验流程为:

①试验钢绞线的截取。截取(105±5)cm长度钢绞线若干用于张拉钻孔试验;②应变片粘贴。每根试件粘贴三枚应变片,具体见图7;③钢绞线张拉及钻孔。利用夹具将试件固定在万能试验机上,通过万能试验机的电控系统设置张拉参数进行钢绞线张拉持荷,待达到预定张拉应力后对钢绞线钻孔。

本试验共设置10组不同工况下的钢绞线进行钻孔,每组工况试验两次,具体包括:外丝钻孔半径0.5 mm工况8组,编号1～8。每组钻孔深度1.0～3.0 mm,初始张拉力分别为0、0.2σcon、0.4σcon、0.6σcon、0.7σcon、0.8σcon、0.9σcon、1.0σcon;外丝钻孔半径0.75 mm工况2组,编号9、10。每组钻孔深度1.0～3.0 mm,初始张拉力分别为0、1.0σcon。其中,1和9组试验为无应力下的钢绞线钻孔,其目的在于得到钢绞线钻孔时产生的加工应变;2～8组为钻孔半径0.5 mm时分别施加0.2σcon、0.4σcon、0.6σcon、0.7σcon、0.8σcon、0.9σcon、1.0σcon张拉应力时的钢绞线钻孔试验,其目的在于建立钢绞线钻孔后孔边应变释放量和有效预应力之间的关系;10组为钻孔半径为0.75 mm时张拉力为1.0σcon的钢绞线钻孔试验,通过和8组试验数据对比验证钢绞线孔边应变释放量受钻孔半径的影响规律。

4.2 盲孔法试验结果

4.2.1 无应力下钢绞线钻孔试验结果

对1组和9组试件进行无应力下钻孔试验。得出钻孔时钻头挤压作用以及钢绞线内部残余应力释放对待测点位应变的影响,对测量结果取平均值,得到不同钻孔半径、钻孔深度下的钢绞线无应力钻孔加工应变,见表3。

表3 钻孔加工应变量

从表3可以看出,随钻孔深度和钻孔半径的增加,钻孔加工应变持续增大,为更精确测得钢丝钻孔后的应变释放量,将下文钻孔后所测数据均扣除相应钻孔加工应变量后列出。

4.2.2 有应力下钢绞线钻孔试验结果

将钢绞线在万能试验机上张拉到预定荷载,然后对已标记的点位进行钻孔,钻孔前后通道1和2测得的应变释放量的平均值作为该试件平均应变释放量,将各组两次试验得到的平均应变释放量取均值得到该组工况下的钢绞线钻孔孔边应变释放量平均值,各组工况下应变释放量平均值随钻孔深度的变化曲线,见图8。

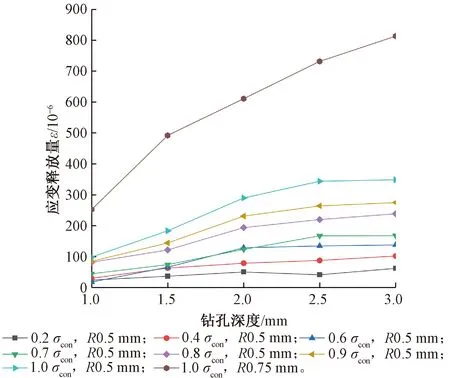
图8 不同工况应变释放量随钻孔深度的变化

由图8可以看出,钻孔半径为0.5 mm的试件,随张拉力和钻孔深度的增加,孔边应变释放量均呈现增大趋势,且当钻孔深度超过2.0 mm时曲线开始收敛,随张拉力逐渐增大,钻孔加工应变等因素的干扰愈发微弱,曲线的变化趋势更为一致。

钻孔半径为0.75 mm试件的孔边应变释放量要远大于同等张拉力下钻孔半径为0.5 mm的试件,且在钻孔深度由1.0 mm变化到3.0 mm的过程中,应变释放量持续增大,没有收敛态势。曲线所显示出的钢绞线钻孔孔边应变释放规律与仿真计算所得基本一致,但又有所区别。仿真计算得出,钻孔深径比在2.0～3.0时,应力释放曲线已达收敛,然而经过试验,发现钻孔半径0.5 mm孔边应变收敛深径比在4.0～5.0,收敛速度明显慢于仿真计算值,经过分析,发现实际钻孔的形状为上粗下细的子弹头状,有别于仿真模拟的圆柱状,从而使二者收敛速度产生差异,见图9。

图9 钻孔形状(单位:mm)

通过改变模型中钻孔形状,使其成为尾部为半径0.5 mm半球的子弹头状,再次进行仿真计算分析验证。与圆柱状小孔相比,子弹头状小孔内部边缘更趋光滑连续,仿真计算结果表明,在同等钻孔深度下,后者孔型情况钢绞线钢丝同一位置处钻孔后孔边应力释放率更低,应力释放量收敛速度更为缓慢,收敛深径比更大,且与钻孔试验结果更接近,表明上述修正后的孔型具有合理性,可信度也更高,二者收敛深径比对比结果见表4。

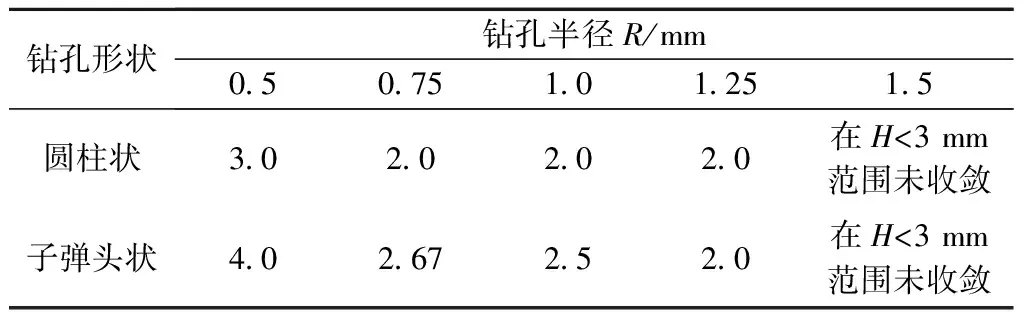
表4 两种孔型钻孔应力释放量收敛深径比对比

另外,通过分析每组试验通道3的数据发现,在钻孔过程中相邻钢丝与钻孔钢丝间的接触摩擦力对钻孔钢丝钻孔后的应力重分布过程起了限制作用,削弱了钢丝钻孔后的拉伸效应,进而导致相邻钢丝在二者相互作用下应变增加,且随张拉力、钻孔深度、钻孔半径的增加,相邻钢丝的应变增幅逐渐变大。以钻孔半径0.5 mm,钻孔深度2.5 mm,初始张拉应力 1 395 MPa 张拉钻孔工况为例,张拉至预定张拉力后3通道应变读数(με)为2 311.0,钻孔后3通道应变读数(με)为2 504.0,钻孔后相邻钢丝应变与钻孔前应变之比为1.084。以上分析表明,钻孔钢丝应力释放后,由于相邻钢丝间接触挤压及其摩擦作用,相邻钢丝应变出现增加,根据本文试验结果最大增长比率在5%～8%范围内。由于本文有效预应力识别拟合公式是以试验结果为基础,实际上已计入这个应力重分布的影响,而且其对应力释放量影响较小,对钢绞线有效应力识别效果不会造成影响。

4.2.3 钻孔应变释放量与钢绞线有效预应力关系

前面分析得出钢绞线钢丝钻孔后孔边应变释放量是随孔深的增加逐渐增加直至收敛,通过钻孔半径0.5 mm试验数据及曲线图可以看出,当钻孔深度超过2 mm时,应变释放量曲线开始收敛;当钻孔深度达到2.5 mm时,应变释放量基本不再随孔深变化。这一规律为寻找钢绞线盲孔法试验时钻孔应变释放量与有效预应力之间的定量关系提供了前提条件。下面基于试验得到的钻孔半径0.5 mm,钻孔深度2.5 mm工况下的实测数据对钻孔应变释放量与有效预应力之间进行最小二乘法曲线拟合。每组试验做2次,每次试验得到通道1和2两组数据,在某一初始应力下按上述工况钻孔获取的数据共4组。拟合曲线见图10。

图10 钻孔应变释放量与有效预应力拟合曲线

拟合函数为二次函数曲线,其方程为

( 2 )

式中:Tc为钢绞线有效预应力计算值;εrs为测点处的应变释放量实测值。拟合曲线的相关系数R2=0.974 1,表明拟合程度较好。

为减小偶然误差,取同一试件上通道1和2的应变释放量的平均值计算钢绞线有效预应力值。为检验拟合公式计算出的有效预应力和实际有效预应力之间的误差情况,现将实测数据代入式( 2 )得到对应有效预应力计算值,可求出有效预应力计算值Tc与真实值T之间的相对误差K为

(3)

图11所示有效预应力计算值Tc与真实值T之间近似呈线性关系变化。经误差分析得到,有效预应力的拟合计算值和真实值之间的相对误差最大值仅为8.82%,且超过85%的数据相对误差在7%以内。以上数据证明利用拟合公式识别该类钢绞线有效预应力具有一定的可信度,可以作为该类钢绞线盲孔法识别有效预应力的经验公式使用。

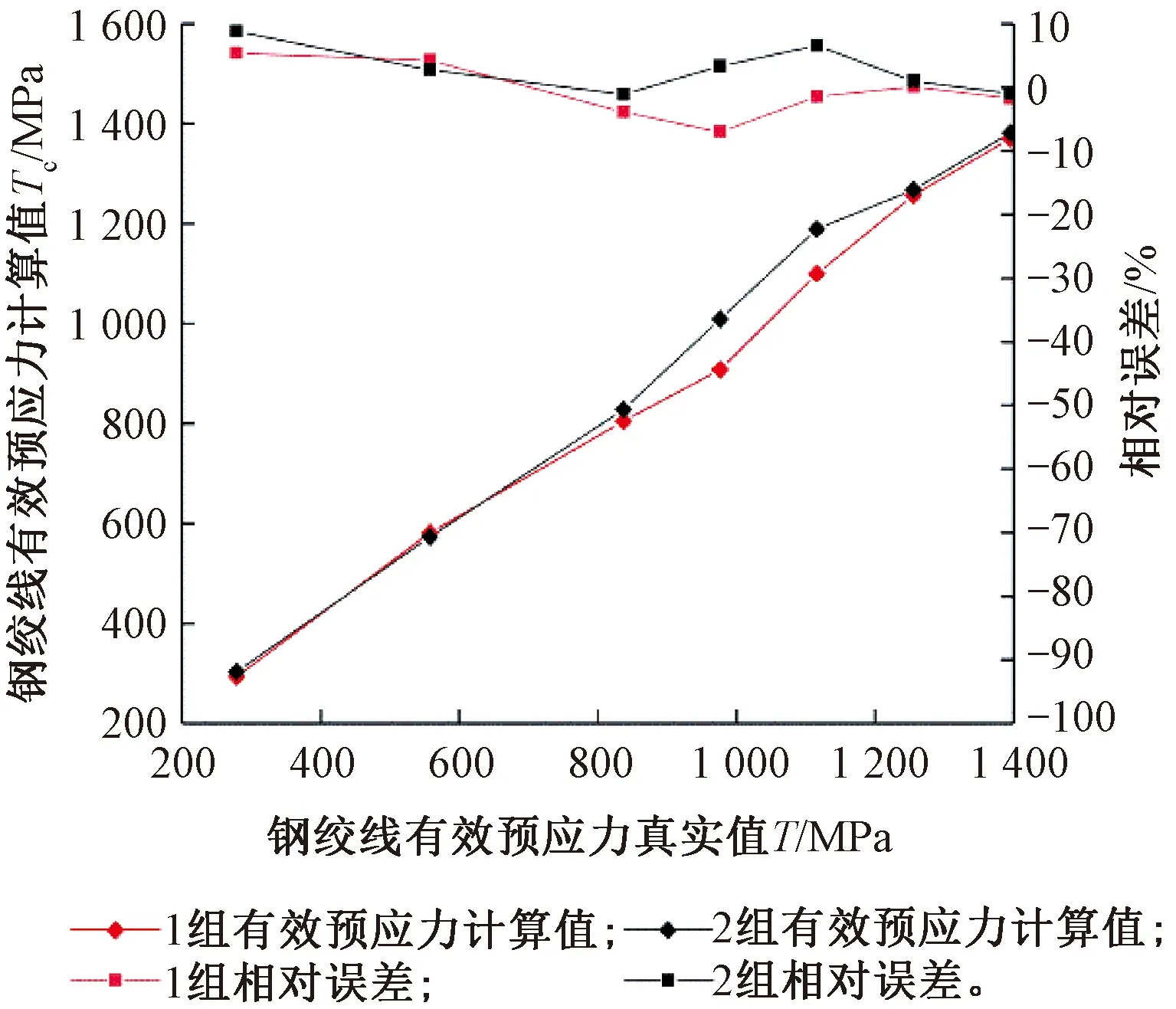
图11 有效预应力真实值与计算值关系曲线

5 结论

本文针对既有预应力混凝土桥梁钢绞线有效预应力识别这一技术难题,在现有研究基础上,提出了钢绞线钢丝盲孔法进行有效预应力识别计算的基本方法,通过理论仿真分析,结合试验结果验证和分析,主要得出以下结论:

(1)钢绞线钻孔后孔边应力释放量及应力释放率随孔边距的增大逐渐下降,且下降趋势由陡峭趋于平缓,对于钻孔半径0.5 mm工况,钻孔对钢丝应力的影响区域约为孔边距5 mm范围内,超过这一范围几乎没有影响。

(2)通过对钻孔半径以及钻孔深度进行参数影响规律分析,发现钢绞线钢丝钻孔后孔边应力释放量随钻孔半径及钻孔深度的增加而增加。当钻孔半径一定时,对圆柱小孔理论上钻孔深径比达到2.0～3.0时孔边应力释放曲线趋于收敛。

(3)通过对钢绞线进行大量钻孔试验验证了仿真计算规律的可靠性,并通过测试结果与仿真模拟存在的差异,深入分析了圆柱形小孔和子弹头状小孔两种不同钻孔形状差异对释放收敛变化的影响,得出后者孔型时收敛深径比取值更大,进一步为仿真模型修正和实际检测数据处理提供了参考依据。

(4)通过对钻孔半径为0.5 mm,钻孔深度为 2.5 mm 工况的实测数据进行拟合,得到了盲孔法试验检测时,钢绞线有效预应力与孔边2 mm测点处应变释放量之间的函数关系,并考虑钻孔偏差修正,经误差分析得出,盲孔法识别钢绞线有效预应力的拟合计算值与真实值之间相对误差最大值为8.82%,且超过85%的数据相对误差在7%以内。由此可以证明盲孔法识别计算钢绞线有效预应力具有可行性。

盲孔法测试识别既有桥梁钢绞线钢丝应力作为一种新型的直接测试方法,最近已有检测单位参考国外相关研究在实际工程中开展了探索性应用,但目前还未检索到公开文献进行实际工程检测的相关报道。作为一种新型测试方法,仍有很多工作值得继续深入研究。根据本文的研究,在采用盲孔法进行实际梁体有效预应力检测时,应避开梁体控制截面,且选取靠近外侧的管道进行测试,测试时需要对测试点附近很小范围混凝土及压浆浆体进行局部凿除,且要避免造成对预应力筋的损伤,测试后再按相关规范要求进行混凝土修补。该法的不足是属于一种局部破损的检测方法,但是根据计算模拟分析有限的小盲孔对整根钢绞线力学性能的影响微乎其微;其优点是一种直接测试方法,具有更高的检测精度和检测效率,可在一定条件下进行使用。由于钢绞线硬度较高,需要专用高强合金钻头才能顺利施钻,专用自动化钻孔设备也需要进一步研发。目前本文仅通过模拟试验进行了相关验证,尚未进行现场实际桥梁试验,今后将通过实际桥梁检测试验进一步完善钢绞线钢丝盲孔应力释放法的理论模型,积累数据,形成系统的检测分析方法,为在役预应力混凝土铁路桥梁有效预应力识别提供一种可行的直接检测方法。