用于贯通式牵引供电系统的级联型变换器可靠性研究

何晓琼，荆 蕾，韩鹏程，曾 理，高仕斌

(1.西南交通大学 电气工程学院，四川 成都 611756；2.国家轨道交通电气化与自动化工程技术研究中心，四川 成都 611756)

牵引供电系统是铁路系统的重要组成部分,能够为列车提供动力来源。随着铁路的高速发展,现行牵引供电系统中存在的电分相、电能质量等方面的问题逐渐突出,成为制约列车速度、运行效率及铁路系统进一步升级发展的问题所在。

随着电力电子技术的发展,新型贯通式牵引供电系统被提出并得到广泛关注[1-4],其系统结构如图1所示。该系统采用交-直-交变换器装置替代传统牵引变压器,可以完全取消电分相,实现全线贯通;同时,新系统还具备便于新能源和储能装置接入的特点,能够实现铁路绿色环保用电,是解决铁路牵引供电技术问题的发展方向。

图1 基于三相-单相级联型变换器的贯通式牵引供电系统

近年来电力电子行业的快速发展为贯通式牵引供电系统的深入研究及推广创造了条件。级联型变换器作为新系统的重要组成装置,由电力电子器件组成,其可靠性研究对于贯通式牵引供电系统的推广及工程应用尤为重要。

目前,常用的可靠性分析方法或模型主要有可靠性框图、故障树、k/n(G)分析法、Markov模型。文献[5-6]根据评估对象组成部分的不同结构形式建立可靠性框图。可靠性框图是对设备内部可靠性连接关系的体现,无法适用于含容错性能的设备。文献[7-8]建立所分析故障事件的故障树评估设备的可靠性方法。故障树是对设备可能发生的所有故障事件进行梳理的可行方法,可以清晰直观地表现出引发设备失效的所有故障事件以及故障事件间的相互关系,适用于对设备进行定量和定性分析。文献[9-11]应用k/n(G)分析法评估模块化多电平换流器的可靠性。该方法能够表征设备在冗余策略下的容错性能,但条件是要求评估对象的n个子系统的失效率在设备全工作过程中保持不变,不适用于子系统失效率会随级联数改变的情况。文献[12-17]采用Markov模型对评估对象进行可靠性评估。该模型是一种动态建模方法,认为评估对象有包括失效状态在内的多种工作状态,通过分析各状态间的转移概率求解评估对象的可靠度,能够充分表征设备容错性能,有利于对设备的可靠性进行准确全面的评估。

贯通式牵引变电所中级联型变换器的工作状态分为正常、存活和失效3种状态,适用Markov理论建立可靠性模型。但现有文献中对评估对象运行工况考虑并不完善,例如存活状态中仅考虑了评估对象部件失效后可维修的状态,未分析评估对象通过降功降额等方式运行的工况;并且,在研究状态间的转移概率时仅通过设备失效率、修复率或是统计数据获取,未有针对非单设备失效或无统计数据的状态进行转移概率求取的研究。

基于上述考虑,本文结合贯通式牵引供电系统所用级联型变换器拓扑结构及工作特点,应用故障树和Markov理论,分级建立级联型变换器可靠性模型,并提出一种考虑正常、存活和失效3种工作状态的状态转移概率计算方法,通过算例分析验证模型的有效性。为提升变换器可靠性以满足工程应用需求,本文基于所建立模型继续研究其可靠性优化方法:定量分析不同关键器件的重要度,辨识出变换器可靠性组成的薄弱环节;在器件和子模块两个层面进行冗余优化研究,并设计综合冗余策略以提升变换器可靠性。本文研究可为贯通式牵引供电系统的工程设计及应用提供依据。

1 可靠性评估指标

可靠性是设备在一定条件下完成指定工作任务的能力体现。选用恰当的可靠性指标对设备进行评估,可以综合性地衡量设备的质量,预估设备的使用寿命。在对设备进行可靠性评估时,通常采用失效率、可靠度函数、不可靠度函数和平均无故障工作时间来分析和表征设备的可靠性能[18]。

(1)失效率是指设备在规定时间内失效的数量与设备总量之比,记为λ(t)。失效率常用单位为fit,表示在109h内,出现一次故障即为1 fit。失效率随时间的变化主要分为3个阶段:早期失效期、偶然失效期和耗损失效期,由于3个阶段失效率表现趋势形似浴盆,被广泛称为“浴盆曲线”,如图2所示。

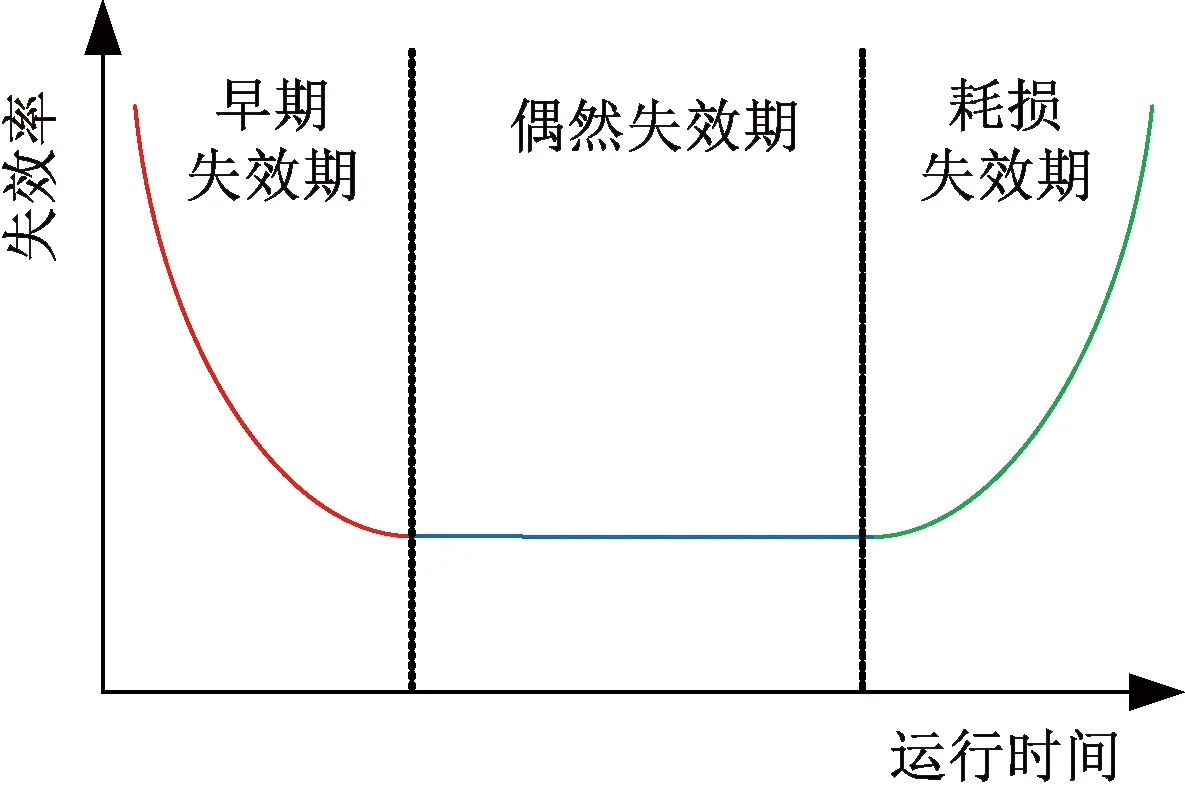
图2 可靠性浴盆曲线

早期失效期可在设备出厂前进行试验筛选以缩短时间,耗损失效期可通过寿命预估并提前更换设备进行避免。因此,通常的可靠性分析针对的是处于偶然失效期的设备失效率,在这一阶段,设备的失效率较为稳定,可近似看作常数,即λ(t)=λ。

(2)可靠度函数是设备在指定条件下完成工作任务的概率关于时间t的函数,记为R(t)。设备在(0,t)时间内,R(0)=1,R(+∞)=0。在设备处于偶然失效期中,失效率近似为常数时,设备的寿命满足指数分布模型,设备的可靠度函数可以表示为

R(t)=e-λt

( 1 )

(3)不可靠度函数,也称失效度,是指设备在指定条件下丧失工作功能的概率关于时间t的函数,记为F(t),可表示为

F(t)=1-R(t)

( 2 )

(4)失效前平均工作时间(Mean Time to Failure),是指设备在发生失效前的平均工作时间,通常表示为MTTF。失效率近似为常数时,MTTF与可靠度函数和失效率之间的关系为

( 3 )

2 变换器可靠性建模

2.1 变换器结构分析

基于级联型变换器的贯通式牵引供电系统的工作原理是:从三相电网取电,经三相整流器后输入直流环节并滤波,再通过单相逆变器逆变输出单相交流电后,输入铁路27.5 kV牵引网为列车供电。贯通式牵引供电系统由多个牵引变电所构成。

级联型变换器是贯通式牵引供电系统变电所结构的核心部分,拓扑结构如图3所示。输出端级联结构能够解决开关器件耐压水平限制的问题,实现全控型电压输出,保证变电所内及各变电所间的输出电压幅值、相位等完全一致,构成全线贯通。

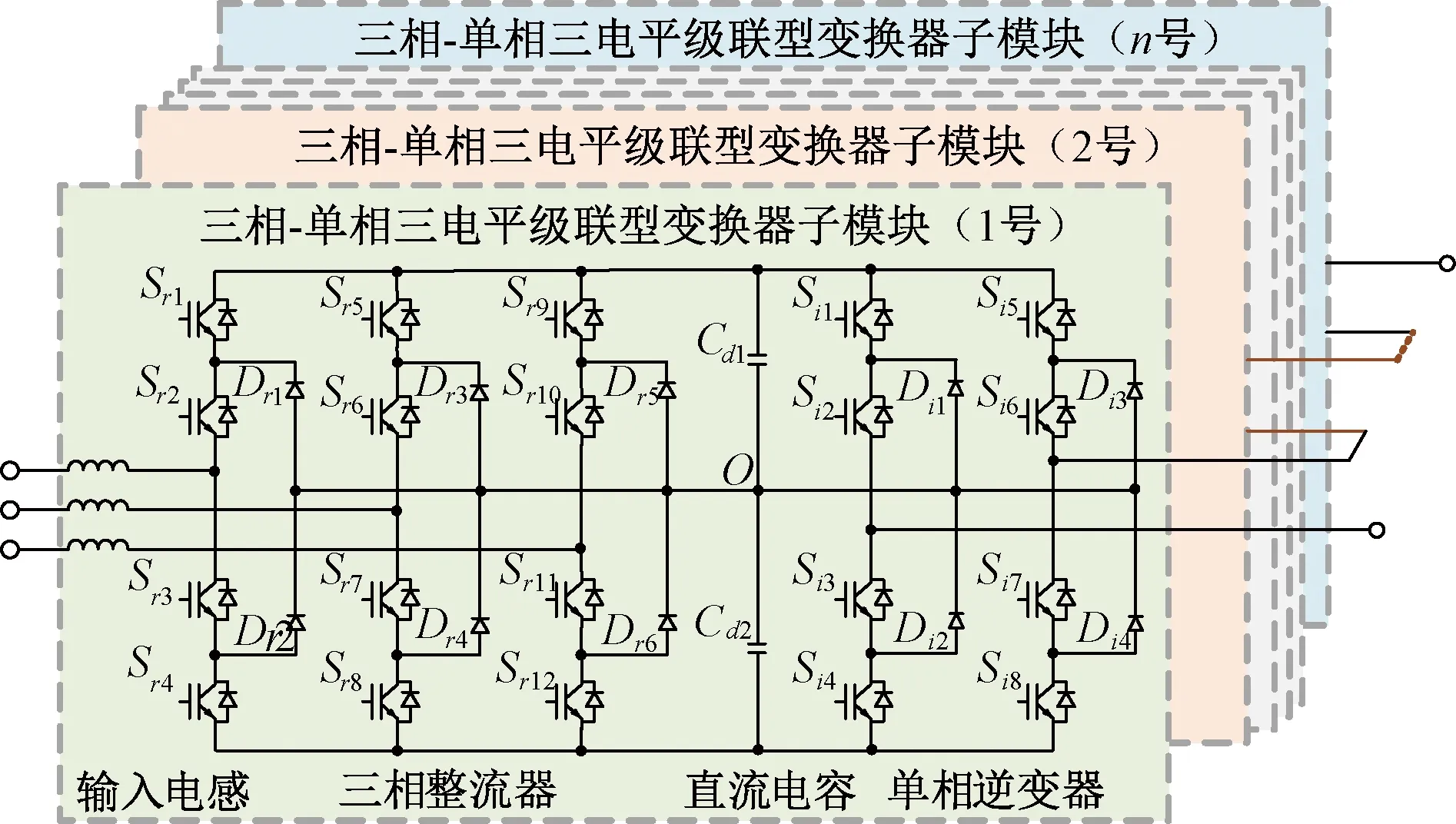
图3 三相-单相三电平级联变换器拓扑结构

级联型变换器子模块是三相-单相变换器,采用三电平二极管钳位拓扑结构。子模块组成主要包括三相侧输入电感组、三相整流器、直流稳压环节以及单相逆变器,变换器的基本组成器件有IGBT、二极管、电容和电感。

2.2 级联型变换器子模块可靠性建模

级联型变换器子模块结构组成如图3中三相-单相三电平级联型变换器子模块(1号)所示。子模块中各个元器件之间的失效率相互独立,且属于不可维修器件,不具备容错能力。基于子模块上述特性,可应用故障树分析法对其进行可靠性建模。

故障树分析法(Fault Tree Analysis,FTA)是将设备可能会出现的所有故障事件进行罗列,并分析故障事件的因果关系后进行建模。以设备最不希望出现的故障情况作为顶层事件,将引发顶层事件发生的故障事件作为次一层事件,如此从顶层向下依次分析,直至分析到最起始的底层事件。

故障树用逻辑门符号描述设备中事件之间的因果关系。逻辑门符号包括“和”“或”“表决”。假设事件A是事件B和事件C通过逻辑门之后的输出事件,并且事件B和C是互斥事件。当事件B和事件C同时发生则事件A才发生时,事件B和事件C通过的逻辑门为“和”,此时事件A发生的概率可以表示为

P(A)=P(B∩C)=P(B)P(C)

( 4 )

当事件B与事件C中任何一种事件发生则事件A就发生时,事件B和事件C通过的逻辑门为“或”,此时事件A发生的概率可以表示为

P(A)=P(B∪C)=P(B)+P(C)

( 5 )

当逻辑门输入事件有n个相同发生概率的事件,其中r个事件发生时,逻辑门输出事件A则发生,这时逻辑门称为“n中取r”表决门,当输入事件的失效度为Fi(t)时,输出事件代表设备的失效度可以表示为

( 6 )

在级联型变换器子模块工作中,其顶级失效模式是自身失效,因此可将顶事件确定为级联型变换器子模块失效事件。由此逐层向下分析,根据子模块分为三相输入侧电感组、三相整流器、直流稳压环节以及单相逆变器四部分,可建立故障树如图4所示。

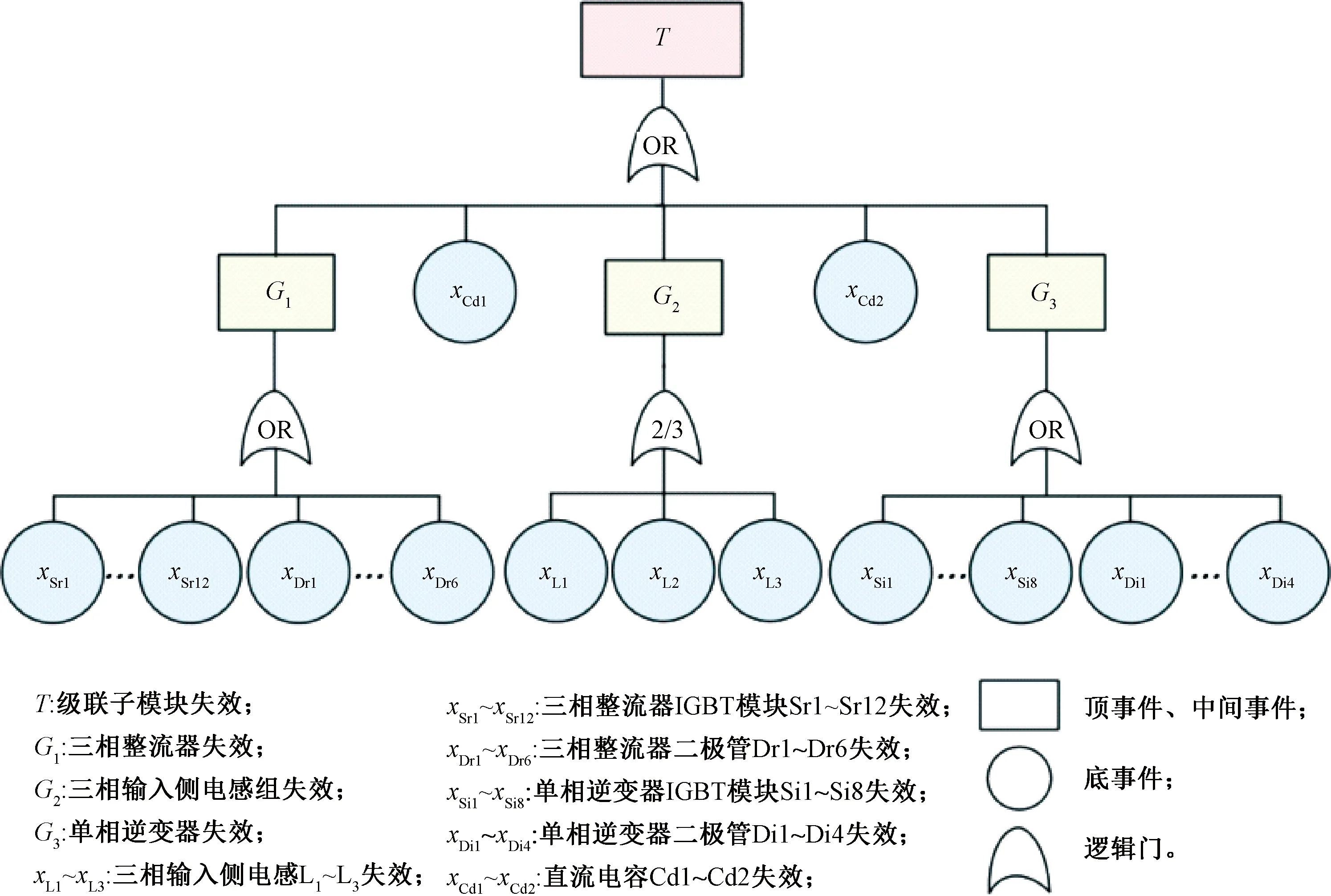
图4 级联型变换器子模块故障树

本文建立的故障树的顶事件是变换器子模块失效,顶事件T的发生概率由其次级事件的逻辑关系以及各事件的发生概率决定。具体来讲,顶事件T的次级事件包括中间事件G1、G2、G3和底事件xCd1、xCd2,其中各事件间的逻辑关系是“或”,即任一事件发生都会导致顶事件发生。根据式( 5 )所示的次级事件间的逻辑关系为“或”时的概率计算公式,可得顶事件的发生概率为

( 7 )

中间事件的发生概率则由各自的次级事件决定。中间事件G1、G3的次级事件间的逻辑关系是“或”,可分别计算出中间事件G1、G3的发生概率。

( 8 )

( 9 )

式中:对于中间事件G2,由于其次级事件输入的逻辑门是表决门,输出事件的发生概率无法直接计算。但由于该事件次级事件均为器件失效事件,根据式( 1 )和式( 6 ),可将其发生概率转换为可靠度进行计算。

各个底事件的发生概率是事件中对应的元器件的失效率。举例而言,事件xSr1表示三相整流器中的IGBT模块Sr1失效,则事件xSr1的发生概率即为IGBT模块Sr1的失效率。

建立的故障树中的中间事件G1、G3是三相整流器、单相逆变器的失效事件,因此中间事件的发生概率即为该三部分结构的失效率。进一步推得级联变换器子模块各部分结构的可靠度函数。

三相整流器的可靠度函数为

RRec(t)=e-12λIGBTt-6λDt

(10)

三相输入侧电感组的可靠度函数为

RL(t)=3e-2λLt-2e-3λLt

(11)

单相逆变器的可靠度函数为

RInv(t)=e-8λIGBTt-4λDt

(12)

级联型变换器子模块的可靠度函数为

RS(t)=e-20λIGBTt-10λDt-2λCt(3e-2λLt-2e-3λLt)

(13)

综上得子模块失效前平均工作时间为

(14)

式中:λL为三相侧电感的失效率;λC为直流稳压电容的失效率;λIGBT为三相整流器和单相逆变器中IGBT模块的失效率;λD为三相整流器和单相逆变器中二极管的失效率。因贯通式牵引供电系统暂无工程运行数据,各器件的失效率尚未有统计数据,进一步的研究可根据文献[19]进行失效率评估。

2.3 级联型变换器可靠性模型

贯通式牵引供电变电所设计中,级联型变换器的级联模块数为8,其中1模块冗余,级联模块数由铁路牵引网压和变换器开关器件IGBT的耐压水平决定,由于篇幅原因,本文不再详细说明,具体设计可见文献[4]。

由于冗余设计,当变换器的8个子模块中1个模块失效时,其余7个模块变换器可正常输出牵引电压。且通过仿真分析及考虑开关管耐压等级可知,当级联变换器中2个模块失效时,可通过降功降额等措施维持运行,此时变换器工作于带故障运行状态,也称存活状态。存活状态下变换器中各元器件承受的电压和电流会发生变化,引起元器件乃至子模块的失效率变化。为更加全面评估变换器的可靠性,需建立考虑存活状态在内的变换器全运行状态可靠性模型,由此引入Markov理论对其进行建模。

Markov过程是指一类在已知现在状态下,未来的演变规律与过去无关的随机过程。对于具体研究对象建立的Markov模型中可包含多个状态,每个状态选择仅与前一个状态有关,且下一个状态的选择是由相应的概率决定的,称为状态转移概率,状态转移概率是不随时间变化的。随机过程{X(t),t∈T}从状态i到状态j的状态间转移概率可表示为

P[X(tk+1)=j|X(tk=i)]Pijk=0,1,…,n

(15)

对于有M个状态的一阶Markov模型,由于每个状态都可能是其余状态的下一个转移状态,可得出共有M2个状态转移以及对应的状态转移概率。该模型的M2个状态转移概率可以表示为一个M阶的状态转移矩阵。

基于上述分析,绘制变换器运行状态的Markov状态转移图,并计算各状态转移概率,可建立全运行状态中子模块变失效率下的级联型变换器可靠性模型。

本文将变换器状态分为正常、存活和失效3种状态。绘制状态转移图时,以状态0表示正常状态,即级联8个子模块中7个及以上子模块正常工作;状态1表示存活状态,具体为8个模块中仅6个模块可正常工作;失效状态是指8个模块中3个及以上模块失效,造成变换器停止工作的状态,表示为状态F。绘制Markov状态转移图如图5所示,λi,j表示变换器从状态i向状态j转移的概率。

图5 级联型变换器Markov状态转移

为简化分析,认为不同子模块失效事件发生均存在一定时间间隔,同时不考虑级联变换器子模块在失效后通过维修重新实现工作功能的情况,即λ0,F=λ1,0=λF,0=λF,1=0。求取其他状态转移概率时,本文提出基于FTA的状态转移概率计算方法,具体流程如下:

(1)确定顶事件为变换器处于状态j的事件。

(2)分析导致顶事件发生的次级事件,记次级事件集合为S。

(3)从事件集合S中选取仅在变换器处于状态i时可能发生的事件,此事件集合记为T。

(4)逐一逐层分析导致集合T中事件发生的次级事件,直至分析出所有事件的底事件,分析不同层级输入输出事件间的逻辑门。

(5)建立故障树模型。

(6)结合式( 1 )～式( 6 ),即可求得顶事件发生概率即状态转移概率λi,j。

由上述流程可以求得状态0向状态1转移的概率为

(16)

变换器从状态1向状态F转移的概率为

λ1,F=6λSi

(17)

式中:λSi为变换器处于状态i时级联子模块的失效率。

变换器任意时刻必处于3种状态中的一种,则有

P0(t)+P1(t)+PF(t)=1

(18)

式中:Pi(t)为t时刻变换器处于状态i的概率。

当Δt趋近于0时,由图5可列写矩阵形式的状态方程为

(19)

变换器处于各状态的概率可通过解式(19)得到,即

(20)

状态0和状态1表示变换器处于可运行状态,变换器的可靠度可由处于此类状态的概率得到

(21)

级联变换器的寿命可表示为

(22)

3 可靠性分析及优化

3.1 关键器件重要度分析

变换器的关键器件包括IGBT、二极管、电容和电感。为辨识级联型变换器可靠性组成的薄弱环节,分别分析每个关键器件的失效率变化对变换器可靠性的影响。由第2节可知,级联型变换器可靠度函数的基本组成是子模块可靠度函数,器件失效率变化对变换器可靠性产生的影响首先体现在子模块可靠性上。因此下文分析将直接以子模块可靠度随器件失效率的变化来表征变换器可靠度的变化。

为对比分析出各器件对变换器可靠性的影响程度,分别假设每个关键器件的失效率从1.5、3.0、5.0到8.0 fit增长变化,并且当假设某一器件失效率变化时,其余器件失效率均设置为1 fit。得到各器件失效率变化对变换器可靠性的影响,如图6所示。

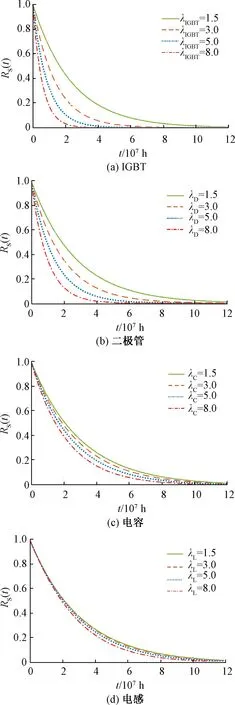
图6 不同器件失效率变化对变换器可靠性的影响

由图6可知,随着失效率由1.5 fit增长至8.0 fit,引起子模块可靠性降低幅度最大的器件是IGBT,可由2×107h时随失效率增加可靠度函数值的下降速率观察得到。由此可知,失效率增加对变换器可靠性影响程度最大的器件是IGBT,其次是二极管,最后是电容和电感。分析主要原因是IGBT在变换器中起开关导通作用,其器件数量最多,当其失效率增加时,变换器可靠性降低程度最大。

为进一步验证IGBT器件相比于其他器件的重要程度,观测变换器在每个关键器件分别设置为100 fit时的可靠性。同时,为突出所观测器件的失效率影响程度,当某一器件失效率设置为100 fit时,其余器件失效率均设置为1 fit。

图7以不可靠度函数FS(t)更加直观地体现器件失效率对变换器可靠性的影响程度。不可靠度为1时表明设备在规定条件下丧失规定功能的概率为100%,即此时设备已完全不可靠。由图7可知,IGBT器件是所有器件中使子模块不可靠度增加速率最快的器件,并在3×107h前使子模块完全不可靠。综合上述分析可进一步确认,变换器可靠性组成中最薄弱环节是IGBT,即IGBT在变换器可靠性组成中的重要度最高。

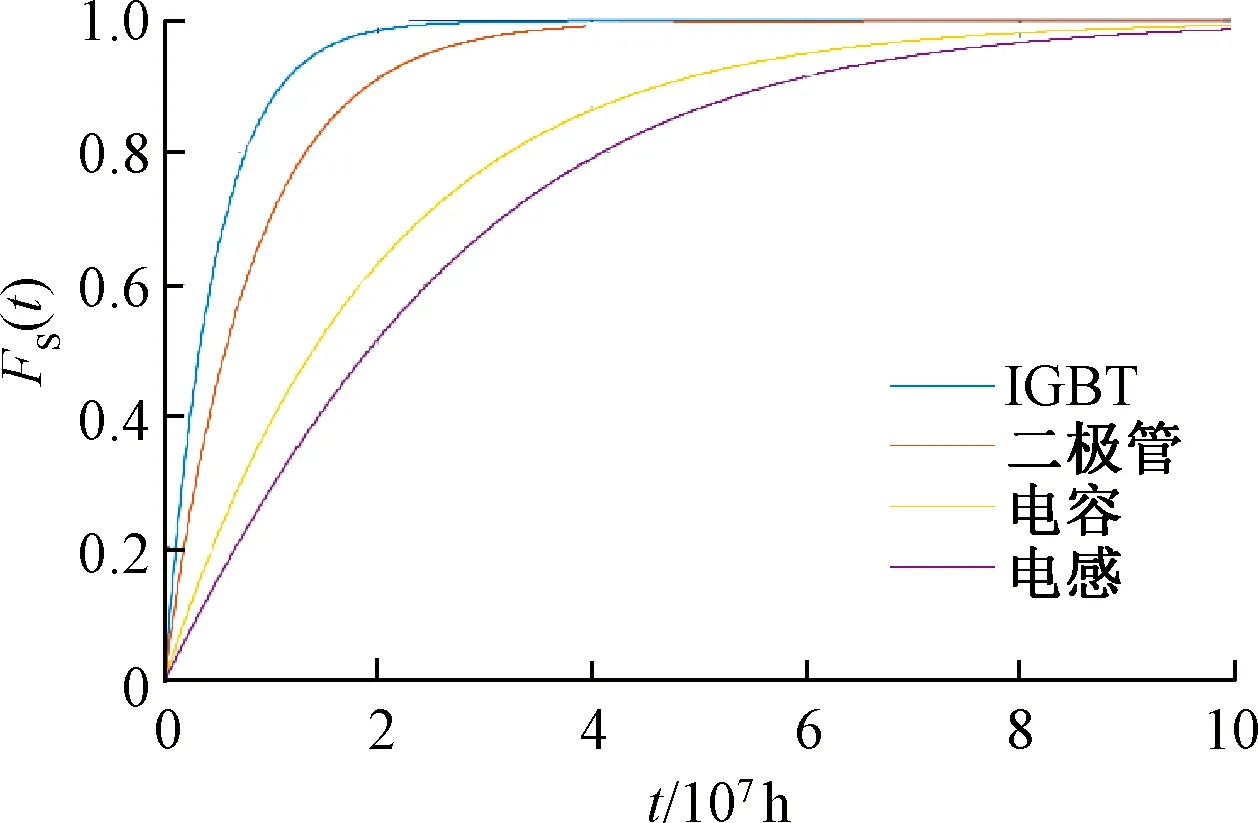
图7 关键器件对子模块不可靠度的影响对比

3.2 可靠性优化

可靠性设计常用的优化策略是冗余设计。既有牵引供电变电所便是采用设备一主一备的方式提高可靠性。但对于贯通式牵引供电系统而言,在所内和所间电分相均取消的情况下,相邻变电所可互为备用,设备冗余策略的优势并不明显,反而会造成总设备占地面积过大、资源浪费的情况。因此,本文不考虑设备冗余策略,将分别从器件冗余和子模块冗余层面分析冗余对变换器可靠性的影响,并设计综合冗余策略,通过算例分析对冗余前后的变换器可靠性进行对比。

3.2.1 器件冗余的影响分析

3.1节中分析出变换器可靠性组成器件的薄弱环节是IGBT,对其进行冗余设计能够大幅提升变换器的可靠性。另一方面,IGBT属于全控型器件,在设置冗余时可通过控制环节进行,无需另配开关。因此,结合经济性和降低控制复杂度方面设计考虑,本文在器件冗余层面仅分析IGBT的冗余策略。

冗余策略分为工作冗余和后备冗余两类。工作冗余是指冗余器件与主用器件并行工作,后备冗余是指平时仅主用器件工作,当主用器件失效时,投入备用器件工作。对每个IGBT分别设计工作冗余和后备冗余,观察两种冗余策略在不同冗余数目下对变换器可靠性的影响。以子模块可靠性变化体现级联型变换器可靠性变化。

工作冗余设计时,子模块可靠度为[18]

e-(λS-λIGBT)t

(23)

后备冗余设计时,子模块可靠度为

e-(λS-λIGBT)t

(24)

式中:n为每个IGBT设计的冗余数目;λS为级联变换器子模块的失效率;λIGBT为单个IGBT的失效率。

因贯通式牵引供电系统暂无可靠性工程统计数据,本算例假设初始值λS=2 300 fit,使用寿命MTTF约为50 a,λIGBT=80 fit,n取0、1、2、3、4。基于式(23)、式(24)、式(14),不同器件冗余数目时,级联型变换器子模块的使用寿命变化如图8所示。

图8 不同器件冗余数目时子模块的寿命变化

由图8可知,两种冗余策略下,子模块的使用寿命均随器件冗余数目的增加而延长。但对比后可发现,后备冗余时子模块使用寿命的提高程度比工作冗余时更具优势,具体数值见表1、表2。

表1 工作冗余时冗余数目n对变换器可靠性的影响

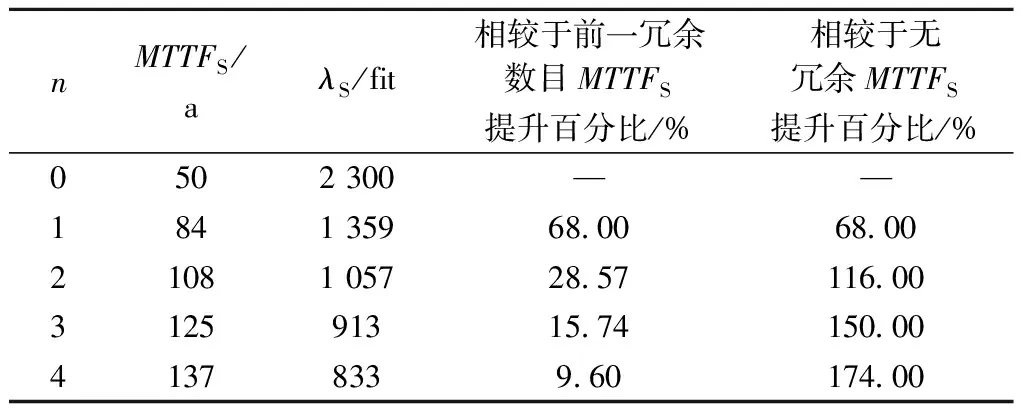
表2 后备冗余时冗余数目n对变换器可靠性的影响

两种冗余策略均在冗余数目为1时,对级联变换器子模块的寿命提升效果最为显著,尤其是后备冗余时相较于无冗余MTTFS提升了68%,是非常可观的可靠性优化效果。

综上分析,结合IGBT无需另设开关便能实现后备冗余的特点,在进行变换器可靠性优化设计时采用IGBT后备冗余策略是较好方案。同时,在考虑经济性的基础上,器件冗余数目建议采用1个。

3.2.2 子模块冗余的影响分析

如2.4节所述,贯通式牵引供电系统所用级联型变换器在设计时采用了7+1模块级联的策略。为验证7+1是否为子模块冗余策略的最佳方案,接下来分析不同子模块冗余度对变换器可靠性的影响。

假设变换器的级联子模块数为7+m,m表示子模块的冗余数目。此时变换器的可靠性模型仍为2.4节所建立的,状态转移图如图5所示。在7个及以上子模块无故障运行时,变换器处于0状态;在仅6个子模块无故障运行时,变换器处于1状态;其余情况下,变换器处于F状态。当子模块冗余数目改变时,状态转移概率λ1,F不变,λ0,1改变,计算流程按2.3节所述。

(25)

本算例取初始值λS0=2 300 fit,λS0=3 000 fit。分别取m=0,1,2,3,4,观测变换器在不同子模块冗余数目时的MTTFN及状态转移率λ0,1的变化。同时,为验证2.4节所建模型的准确性,将算例评估结果与不考虑存活状态时的可靠性评估结果进行对比。不考虑存活状态时的变换器寿命为

(26)

由图9中MTTFN的变化趋势可知,变换器的使用寿命与子模块冗余数目成正相关,且增长速率随冗余数目增加逐渐变缓。状态转移率λ0,1则与m成负相关。分析原因为:当m增加时,变换器的可靠性加强,变换器在下一时刻处于正常工作状态的转移率1-λ0,1增加,故而λ0,1减小。

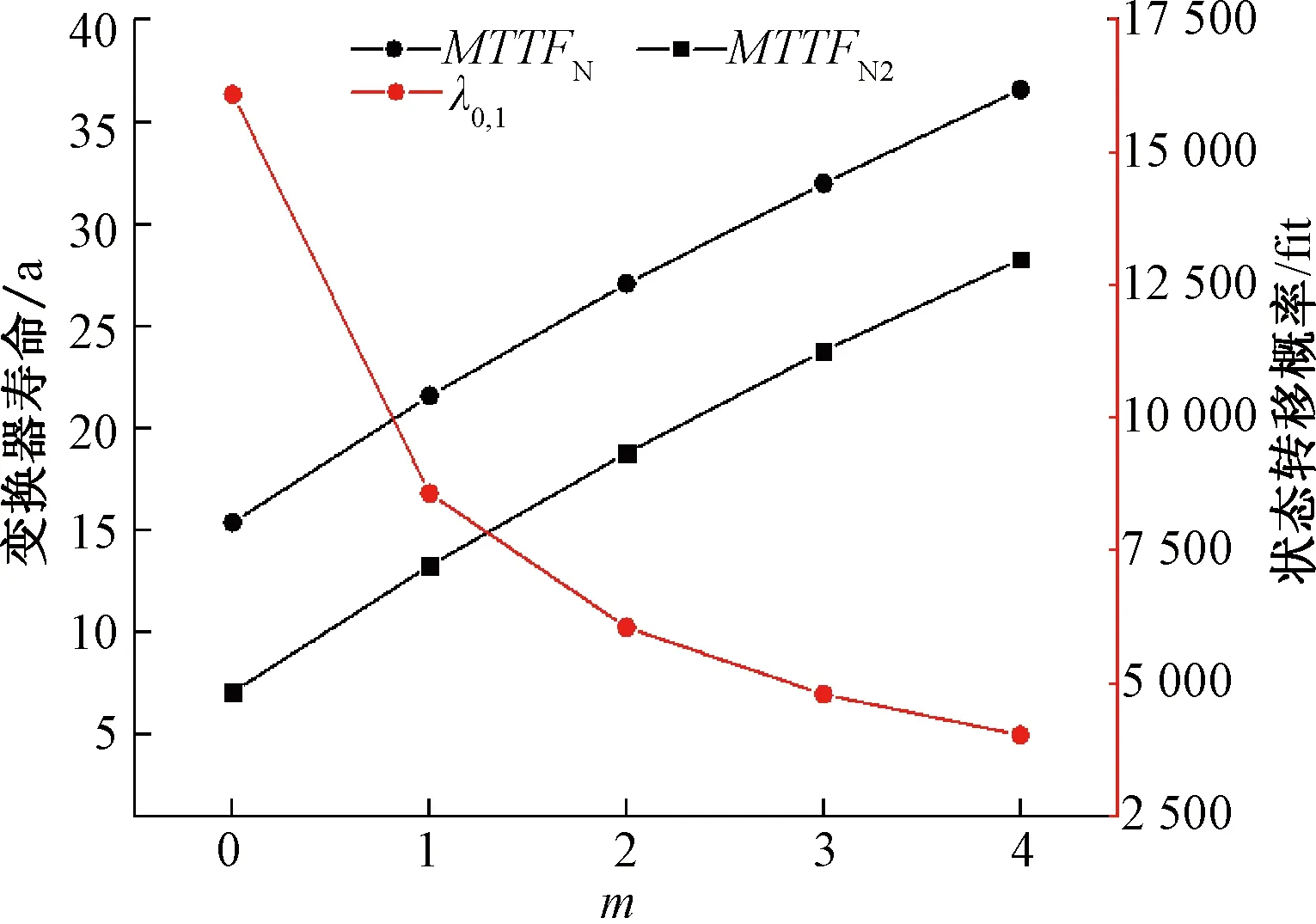
图9 不同子模块冗余数目时的可靠性指标变化

当m取值相同时,MTTFN>MTTFN2,表明本文所建立的考虑存活状态的可靠性评估模型比未考虑存活状态时要更加精确。两者之差ΔMTTF为定值,ΔMTTF≈8.3。该值是考虑存活状态与否的两种评估模型的相差体现,与变换器存活状态时的子模块失效率有关,由前文分析可知,无论m是否变化,λS1均是变换器中仅6个子模块工作时的子模块失效率,是不改变的,故ΔMTTF亦不变。

对表3分析发现,虽然变换器在子模块数7+1时的寿命相比于前一冗余度提升的百分比最高,为40.26%,但在冗余3模块时,变换器寿命比无冗余时的寿命提升了1倍,与既有牵引供电变电所中变压器一主一备的设计寿命提升度相当。故该算例中本文推荐变换器采用子模块数目为7+3的冗余设计方案。

表3 子模块冗余数目m对变换器可靠性的影响

选取合适的子模块冗余数目是系统工程设计中至关重要的环节,本文从冗余对可靠性优化影响这一维度,提出优化度评估方法并进行算例验证。在实际工程设计中,冗余数目还需综合考虑并建立包含经济性、空间利用率的多维度模型进行选择。

3.2.3 综合冗余优化有效性分析

基于前文的分析结果对变换器进行综合冗余设计,具体设计为每个IGBT器件后备冗余1个,子模块工作冗余3个。算例取初始值λIGBT=80 fit,λS=2 300 fit,对综合冗余前后的变换器可靠性指标进行计算,对比结果如表4和图10所示。

表4 综合冗余前后的变换器可靠性指标对比

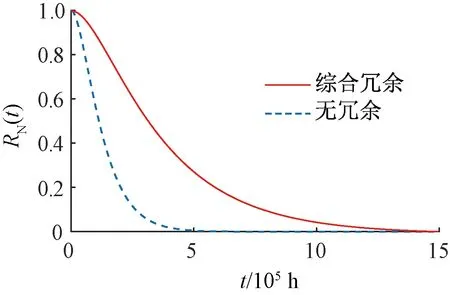
图10 综合冗余前后的变换器可靠度函数对比

由表4可知,综合冗余下的变换器失效率相比于无冗余时降低了66.02%,变换器寿命由15.4 a提升至45.2 a,提高百分比为193%,是无冗余时寿命的近3倍。从图10也可以看出,综合冗余设计后变换器的可靠度下降速率相较于无冗余更低,同时说明变换器在同一时期的可靠度更高。综上分析,综合冗余是对变换器进行可靠性优化行之有效的设计策略。

4 结论

本文针对级联变换器的可靠性组成特点,对子模块进行故障树建模,根据级联变换器的正常、存活及失效状态,基于Markov理论建立级联变换器可靠性评估模型,并提出状态间状态转移概率的计算方法。通过算例分析可以得到如下结论:

(1)本文提出的分级建模既能够有效评估变换器的可靠性,又便于对不同的可靠性优化策略进行对比分析。并且,考虑变换器存活状态后建立的可靠性模型与不考虑存活状态相比,更加符合实际情况。

(2)IGBT是变换器可靠性组成的最薄弱环节。除在选型时选用失效率较低的器件外,可通过器件冗余设计对薄弱环节进行加强。基于经济性考虑,IGBT后备冗余1个是本文建议的最佳冗余策略。

(3)子模块工作冗余设计后变换器的可靠性有明显提升,且变换器的寿命提升幅值并未随冗余数增加有较大下降。读者在实际设计时可按期望寿命及工程设计需求进行冗余数目的选择。

(4)结合器件冗余和子模块冗余的综合冗余是对变换器进行可靠性优化的重要策略,且对变换器可靠性提升效果显著。