一种缩短虚拟编组列车追踪间距的鲁棒模型预测控制方法

罗啸林，唐 涛，林炳跃，刘宏杰

(1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.中国铁道科学研究院集团有限公司 通信信号研究所，北京 100081；4.北京交通大学 轨道交通运行控制系统国家工程研究中心，北京 100044)

轨道交通安全、高效、便捷的优点使其成为公众出行的首选方式。面对不断增长且时空分布极不均衡的客运需求,运营管理部门既希望提升轨道交通最大运能以满足高峰客流需求,又希望能够根据客流实时变化,动态灵活地调整列车开行方式,在不降低乘客服务质量的前提下降低平峰时期的运输成本。针对该问题,可随着客流需求的变化而动态编组或解编的虚拟编组列车受到了业界的广泛关注[1]。

虚拟编组列车由两个及以上数量的单元列车构成,见图1。各单元列车根据与其他单元列车的实时交互信息控制本列车的牵引和制动行为,以保持较小的追踪间距运行。通常将第一辆单元列车称为领航单元列车,后续的各单元列车均称为跟随单元列车。目前,轨道交通列车大多采用固定的编组方式(如物理编组)运行,且编组方式在运行过程中不会改变,难以完全满足运力灵活调整的需求[2]。而虚拟编组单元列车间采用基于相对制动距离的方式防护行车安全,该方式可极大地缩短列车追踪间距,使得虚拟编组列车拥有与物理编组列车一致或接近的运行方式,从而提升轨道线路运输能力[3]。此外,虚拟编组列车还能够在不停车甚至不减速的情况下进行动态地编组和解编[4]。虚拟编组已成为目前轨道交通的研究热点。

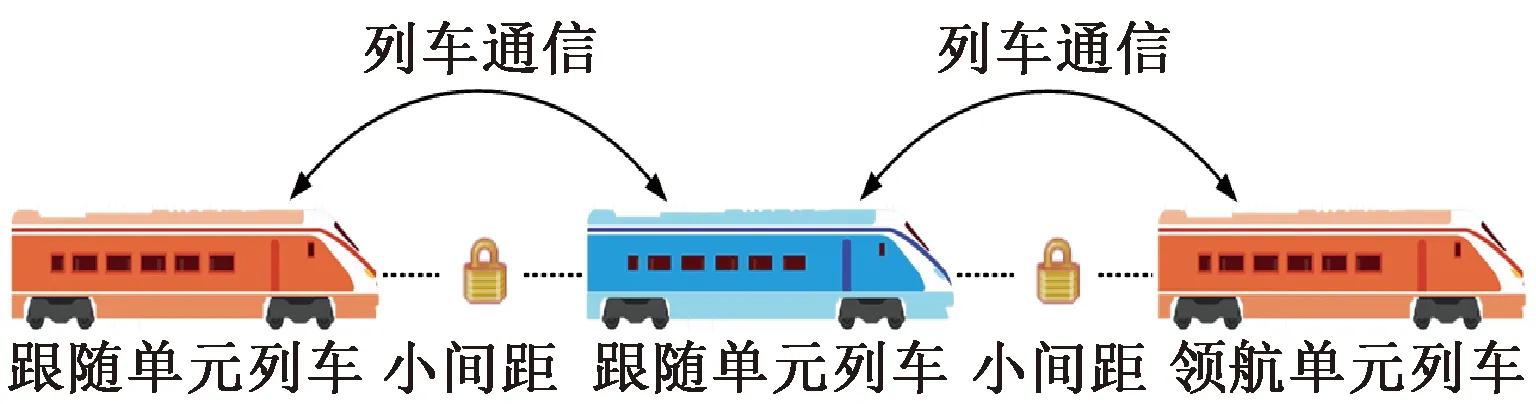
图1 虚拟编组列车

由于相邻单元列车不进行物理连挂,在运行过程中,彼此之间无法依靠车钩传输作用力而维持适当的小间距。因此,为实现虚拟编组列车安全运行,除了要保证各单元列车速度不超过轨道限速,还要保证单元列车追踪间距不小于安全防护距离。而虚拟编组列车运行控制系统不仅要满足上述安全约束条件,还要通过实时调整列车牵引力和制动力使得列车按照期望的方式运行,避免导致输出不必要的紧急制动影响运行效率。针对该虚拟编组列车运行控制问题,已有一些学者展开了研究[5-9]。Quaglietta等[5]根据列车动力学特点设计一种反馈控制律,控制虚拟编组内单元列车保持加速度一致。Di等[6]提出一种基于多智能体的虚拟编组列车运行控制方法保证单元列车追踪间距维持在期望值。但是,以上研究在设计控制方法时并未充分考虑虚拟编组列车在运行过程中受到的安全约束。此外,在虚拟编组中前车的状态决定了后车的控制目标与安全约束,因此应该合理地对未来可能发生的变化做出规划。为控制虚拟编组单元列车在满足各类安全约束时保持较小的追踪间距运行,一些学者提出基于模型预测控制(Model Predictive Control,MPC)的虚拟编组列车追踪控制方法[7-9]。

MPC方法通过构建一个以当前系统状态为输入的有限时域约束最优控制问题,并在线对其求解,得到未来一段时间内的最优控制输入序列,将该序列中的第一个值作用于被控系统,并在下一控制周期重复上述过程,实现系统的在线迭代最优控制[10]。针对虚拟编组列车追踪控制问题,文献[8-9]基于不存在未知干扰的理想环境,利用MPC方法控制虚拟编组列车在满足各类安全约束的前提下维持期望的追踪间距。但实际列车运行过程中存在的诸多不确定干扰会令控制效果出现偏差,从而导致列车违背安全约束。为解决干扰条件下的约束满足问题,Mayne等[11]提出一种基于Tube的鲁棒MPC(RMPC)方法,其原理见图2。首先通过RMPC的鲁棒性使被控系统的实际状态始终保持在距预测状态有界的误差范围之内,进而只要使误差范围内所有可能的实际状态都满足约束条件,就能够保证实际被控系统满足约束。该研究对本文针对不确定干扰环境提出基于RMPC的分布式虚拟编组列车追踪控制方法具有重要借鉴意义。

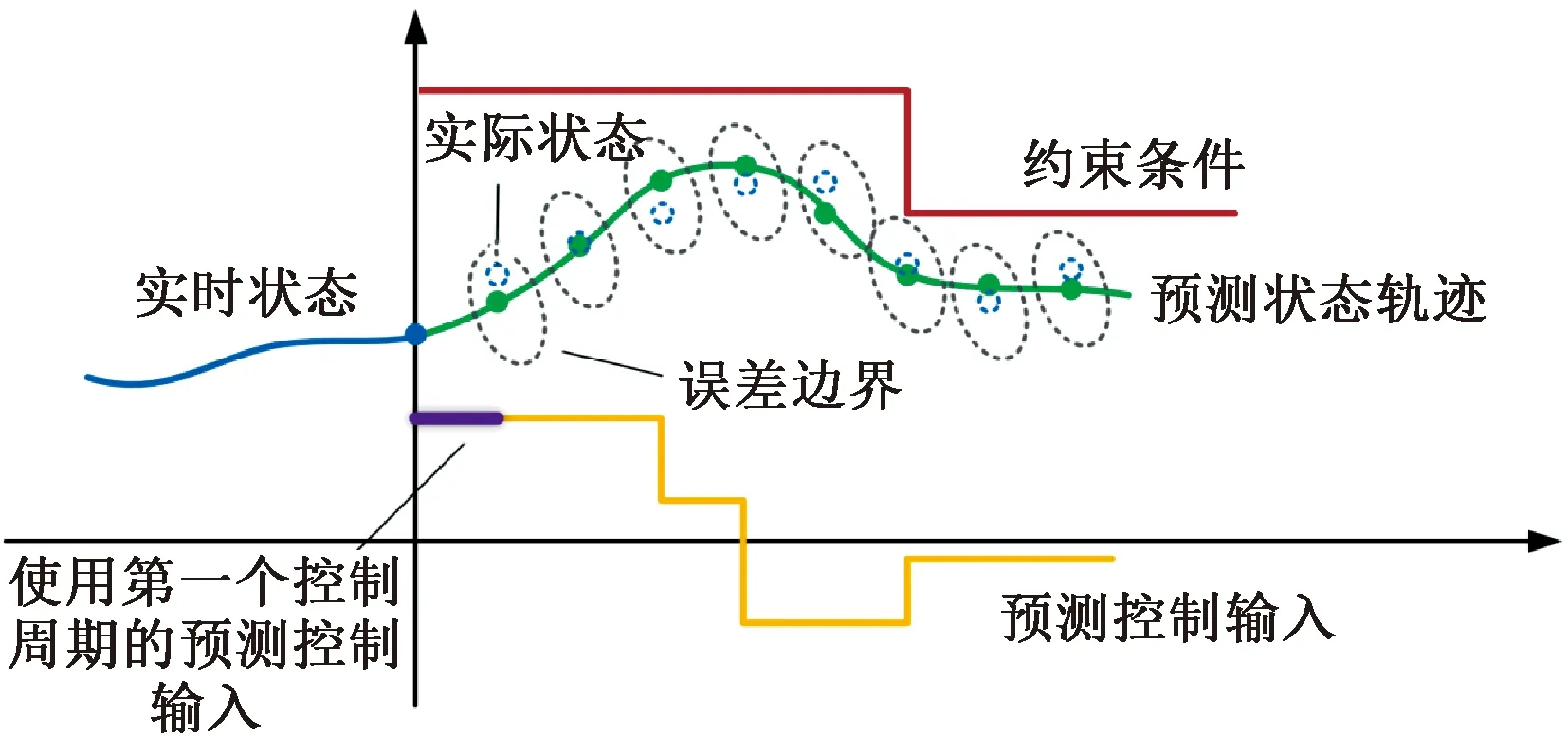
图2 RMPC原理

除保证列车在运行过程中满足安全约束之外,虚拟编组还要求单元列车保持较小的追踪间距。但更小的单元列车追踪间距增大了违背安全约束的风险,这时对追踪控制方法提出了更高的要求。为保证满足安全约束,RMPC在规划时考虑潜在的控制误差,因此,预测轨迹会与安全约束保持一定距离。而减小控制误差范围则能够允许RMPC的预测轨迹更逼近安全约束,进而为单元列车保持更小的追踪间距提供了可能性。Yang等[12]提出一类基于自适应观测器的RMPC方法,其自适应机制能够缩小被控系统实际状态与观测状态的误差,提升性能表现。此后,Yang等[13]通过优化鲁棒控制器参数进一步缩小了RMPC的误差范围。受到上述文献设计理念的启发,并结合文献[14]中的基于线性矩阵不等式(LMI)的鲁棒控制方法,设计一种优化算法以减小本文提出RMPC方法的控制误差。此外,考虑列车的控制输入饱和问题导致列车控制输入的大小会受到一定限制[15],在算法设计过程中对列车控制输入的大小进行了相应的限制,以保证所设计算法的实用性。本文的主要贡献如下:

(1)考虑列车运行过程中的不确定干扰,提出一种基于RMPC的分布式控制方法,保证了虚拟编组单元列车追踪间距的有界性,同时还保证了虚拟编组列车运行的安全性,满足速度安全约束与追踪间距安全约束等。

(2)设计一种基于LMI的优化算法,在输入饱和条件下减小RMPC控制器的控制误差,达到进一步缩短虚拟编组单元列车追踪间距的目的。

(3)基于典型的城轨线路数据和车辆参数,对由3辆单元列车构成的虚拟编组列车,在一个站间的完整运行过程进行了数值仿真实验,并与现有文献中的方法进行对比。仿真结果证明本文所提出基于RMPC的虚拟编组列车控制方法及其优化算法的有效性,在不确定干扰环境下的单元列车追踪间距可从10 m缩短至5.05 m。

1 虚拟编组列车运行控制模型

1.1 列车动力学模型

列车动力学模型作为虚拟编组列车控制的基础,可基于牛顿力学方程将其建立为

( 1 )

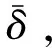
( 2 )

式中:xi(t)=[si(t)vi(t)]T为单元列车i的状态向量;ωc=[0δ(t)]T为列车动力学模型中的有界不确定成分;矩阵Ac和Bc为状态空间方程的参数,满足

( 3 )

实际中,列车状态信息通常以离散采样的方式获取。为方便控制器设计,可通过零阶保持器将连续空间状态方程转化为离散形式,即对于任意的t∈[kτ,(k+1)τ],保持ui(t)=ui,k,其中,τ为离散系统采样间隔时间,ui,k为离散系统控制输入在第k个采样时刻的值。则式( 2 )的列车状态空间方程可转换为如下离散形式

xi,k+1=Axi,k+Bui,k+Dω

( 4 )

式中:xi,k=[si,kvi,k]T为列车i在第k个采样时刻的状态;ω对应列车动力学模型中的不确定成分。由于ωc有界,经过离散化得到的ω能够继承其有界的性质,满足|ω|≤1。各参数矩阵分别满足

( 5 )

1.2 虚拟编组列车最优控制问题

虚拟编组期望各单元列车保持尽可能小的追踪间距。在本文中,要求领航单元列车根据调度指挥系统的指令,以尽可能高的速度运行;跟随单元列车则根据车车通信接收到的前车状态与控制信息,通过调整其控制行为,尽可能减小与前车间的追踪间距。为便于理解,将单元列车追踪间距定义为si-1,k-L-si,k,其中L为单元列车车长。在运行过程中领航单元列车需要满足速度约束,而跟随单元列车需要同时满足速度约束与安全防护距离约束。

根据上述设计,可以定义虚拟编组列车的最优控制问题

( 6 )

要求满足状态空间方程(4)和以下约束

( 7 )

Xs(xi-1,k):={x:Z2x≤Z2xi-1,k-L-sm}

( 8 )

( 9 )

2 面向虚拟编组的分布式鲁棒模型预测控制器

根据虚拟编组列车最优控制问题,首先设计分布式RMPC方法对其进行求解。以下将证明在不确定干扰环境下,仍然能够保证各单元列车满足安全约束条件式(7)～式(9)。

2.1 虚拟编组列车RMPC控制器设计

为实现虚拟编组列车的安全和鲁棒控制,首先根据列车动力学方程(4)中的确定部分,建立名义预测状态的状态空间方程

(10)

(11)

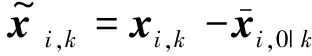
(12)

由于RMPC要求控制误差始终保持在一个有界的范围之内,因此,要求控制误差满足命题1的规定。

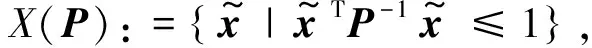
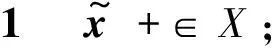
条件2KX∈U,其中U:={u|u≤μ}。

命题1中的条件1保证了鲁棒反馈控制器K能够使得控制误差始终保持在一个有界的范围内。考虑到列车控制输入饱和问题,若反馈控制输入的可行空间过大,则会过多地占用名义控制输入的可行空间,影响RMPC的控制效果。因此,认为该部分控制输入需要满足还要求列车反馈控制输入满足命题1中的约束条件2。认为反馈控制律K能够使得命题1成立,具体的设计方法将在后文中给出。

由于虚拟编组内各单元列车需要分别控制本车运行,将式(6)转换为面向不同单元列车的分布式最优控制问题。由于跟随车的控制目标和约束均与其前车相关,为获得更好的控制效果,本文基于文献[18]中的序列分布式结构设计单元列车的分布式RMPC控制器。即前车RMPC对本车的最优控制问题求解,得到本车最优控制输入序列和相应的本车预测状态序列,并将其发送给后车;后车将前车预测状态序列代入本车的RMPC最优控制问题中并进行求解,得到本车最优控制序列和相应的本车预测状态序列;依次传递,直至虚拟编组的最尾端的单元列车。

根据以上分布式结构,构造虚拟编组中各单元列车的目标函数为

(13)

满足名义预测状态空间方程(10)和

(14)

(15)

(16)

(17)

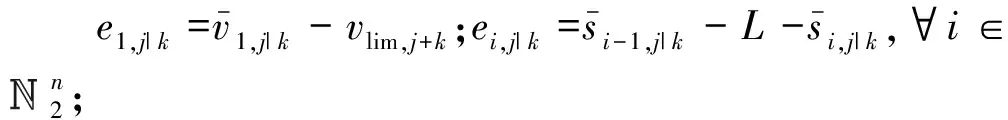
2.2 列车安全约束满足条件

在本节中将证明在不确定干扰环境下,仍然能够保证各单元列车满足约束条件式( 7 )～式( 9 )。首先,给出如下引理保证实际状态处于名义预测状态的有界误差范围之内。

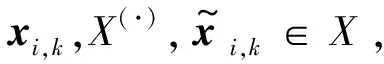
证明:

根据列车实际状态方程,可得

(18)

(19)

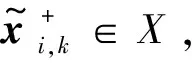
接下来,给出定理1,以保证各单元列车在k+1时刻能够满足约束条件式( 7 )～式( 9 )。

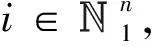
证明:

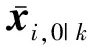
(20)

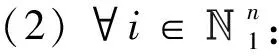
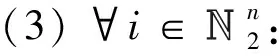
(21)

于是有

(22)

以上,证明各单元列车在k+1时刻能够满足约束条件式( 7 )～式( 9 ),证毕。

3 基于LMI的鲁棒控制器优化算法

本文中RMPC的控制目标是:在满足安全约束条件的前提下提升领航单元列车的行驶速度,并缩短跟随单元列车与前方单元列车的追踪间距。根据命题1可知,通过减小鲁棒不变集X(P)的大小可以减小控制误差;而根据约束条件式(15)和式(16)可知,若控制误差越小,则允许的领航单元列车速度越快、相邻单元列车的追踪间距越小。基于此,可通过优化鲁棒控制器的设计达到提升虚拟编组列车运行控制性能的目的。

3.1 鲁棒控制器设计原理

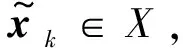
(23)

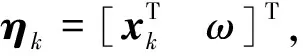
(24)

(25)

基于文献[14],可建立以下定理2并据此设计满足要求的鲁棒反馈控制器K。

定理2考虑K=MP-1,则当且仅当以下不等式成立时

(26)

式中:I为单位矩阵;M为中间变量。

此外,为满足命题1中的条件2,要求式(27)成立

(27)

根据集合X(P)的定义,则式(27)成立的充分条件是

(28)

其等价于

(29)

令不等式两边分别左乘、右乘矩阵P,得

(30)

对其应用舒尔补,可得式(27)成立的充分条件

(31)

综上,可建立定理3使得命题1中的条件2成立。

定理3考虑K=MP-1,当以下LMI成立时,不等式(31)成立,进而条件KX∈U成立。

(32)

证明过程详见文献[19]。

至此,已经可以通过定理2和定理3来设计满足命题1的控制器K。接下来将据此设计优化算法,通过减小控制误差使单元列车的追踪间距更小。

3.2 追踪间距优化算法

由于通过减小鲁棒不变集X(P)的大小可以减小控制误差,因此,可以通过减小集合X(P)的面积来达到缩短单元列车追踪间距的目标。根据文献[20]可知,一种减小鲁棒不变集X(P)面积的方式是减小矩阵的迹trP的大小。因此,通过求解以下优化问题达到设计优化算法的目的

(33)

要求满足约束条件式(26)和式(32)。

若将参数α视为变量,则不等式(26)将不具有LMI形式,从而极大增加问题式(33)的求解难度。针对该问题,一种常用的做法是,将α设置为一个常数值,使不等式(26)变为LMI,再基于此对问题式(33)进行求解。然而,选择不同的α值会得到性能不同的鲁棒反馈控制器K与集合X(P)。因此,我们设计以下算法,通过迭代修改α的方式来获得trP的最小值,尽可能保证所求解对于问题(33)的最优性。

算法1:

参数:β,γ;

初始化:

i=0,α0=1-β,α*=0,f*=+∞,K*=0,P*=0;

步骤:

(1)Whileαi>βdo

(2)α=αi;

(3)求解问题式(33);

(4)If 问题式(33)存在可行解(Mi,Pi) then

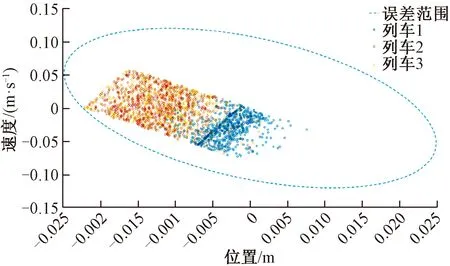
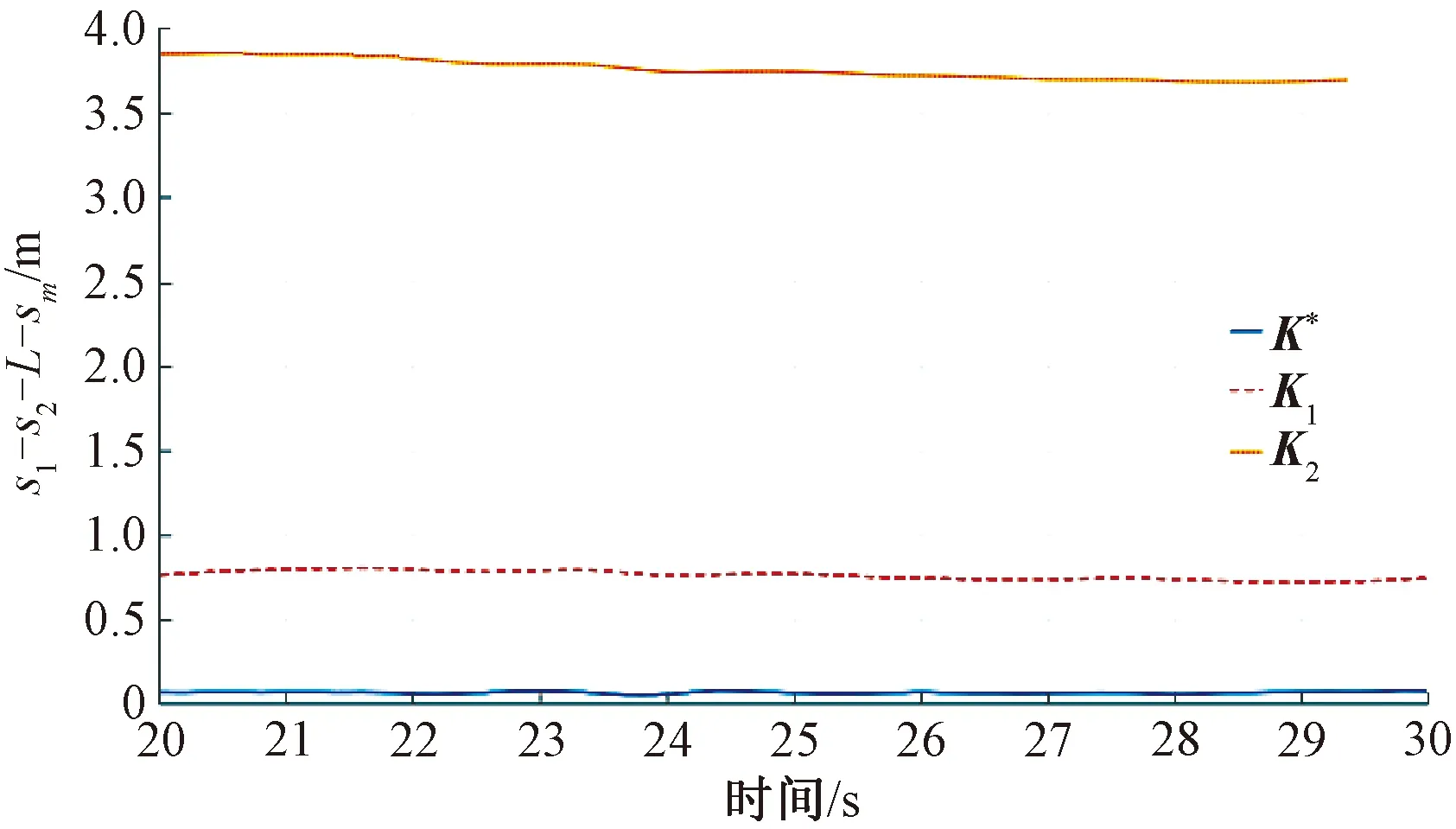
(6)Iffi

(7)α*=αi,f*=fi,K*=Ki,P*=Pi;

(8)αi+1=γαi;

(9)i=i+1;

其中,上标*为变量的优性;β为迭代算法的终止条件,满足0<β<1;γ为变量α的衰减系数,满足0<γ<1,更大的γ值意味着更小的搜索步长。由于算法1是离线求解的,因此可以根据需要选择足够小的β与足够大的γ,从而得到足够精确的解。

4 仿真实验及结果分析

本章将通过实验本文所提出方法的有效性进行验证。首先,将验证通过算法1能够减小集合X(P)的面积;接着,将验证所提出的RMPC方法的有效性;最后,与现有文献中的方法进行对比,验证本文所提出的方法能够缩短虚拟编组单元列车追踪间距。仿真实验中用到的参数及其取值如表1所示。

表1 文中参数取值

4.1 鲁棒不变集优化结果

图3 鲁棒不变集大小比较

4.2 虚拟编组列车站间运行过程仿真结果

本节将验证所提出RMPC方法的有效性。对由三辆单元列车构成的虚拟编组列车,在城轨站间的完整运行过程进行了仿真实验。由于在实际中列车受到的附加力通常以阻力形式存在,因此,认为实验中的不确定干扰满足ω∈[-1,0],其概率密度函数设为f(ω)=1。值得说明的是,当ω∈[-1,1]时,所提出的方法仍然适用。

图4给出了三辆单元列车在站间运行过程中的位置-速度曲线,可看出各单元列车的实际速度均满足约束(7);图5中给出了各单元列车实际追踪间距与对应的安全防护距离的差值随时间变化的情况,可看出各单元列车的实际运行间距始终大于安全防护距离,说明所提出的RMPC控制方法能够保证单元列车追踪间距满足安全约束条件(8)。通过以上两方面可证明所提出的虚拟编组列车控制方法的安全性。图6所示为三辆单元列车运行过程中的控制误差,可以看出虚拟编组内所有单元列车每个时刻的控制误差都处于鲁棒不变集内,说明所提出RMPC方法的鲁棒性。

图4 虚拟编组列车站间运行场景

图5 虚拟编组单元列车实际追踪间距与安全防护距离之差

图6 单元列车运行控制误差

为证明所提出的RMPC方法以及优化算法在缩短单元列车追踪间距方面的有效性,选择文献[8]中的MPC控制方法以及其他两种RMPC方法,与本文所提出的方法进行对比。其中,文献[8]中的列车追踪间距保持为10 m;第一种作为对比的RMPC方法中的鲁棒反馈控制器来自顶级期刊的经典文献[12],其目的是同时减小控制误差及加快状态收敛速度,反馈控制律可相应设计为K1=[-1.046 8 -1.859 6],对应的最大位置误差为0.380 3 m;第二种作为对比的RMPC方法基于未经优化的鲁棒反馈控制器,其反馈控制律设计为K2=[-0.624 8 -1.620 9],对应的最大位置误差为1.939 3 m。分别应用不同的RMPC方法进行实验,得到的单元列车实际追踪间距变化规律见图7。实验结果表明,应用本文提出的RMPC方法及其优化算法后得到的单元列车追踪间距平均为5.05 m;与普通MPC方法[8]得到的列车追踪间距为10 m、未经优化的RMPC方法得到的列车追踪间距为8.88 m以及基于文献[12]的RMPC方法得到的列车追踪间距为5.76 m相比,列车追踪间距缩短幅度分别达到49.5%、43.1%和12.3%。由此可见,本文所提出的方法可显著缩短虚拟编组单元列车追踪间距。

图7 应用不同控制方法的单元列车追踪间距

5 结论

针对虚拟编组列车在不确定干扰条件下的小间距安全追踪控制问题,首先提出一种基于分布式RMPC的虚拟编组列车追踪控制方法,保证单元列车运行速度和追踪间距安全、有界,进而实现了虚拟编组列车小间距鲁棒运行;接着,设计一种基于LMI的优化算法,通过减小RMPC控制器的控制误差,达到进一步缩短单元列车追踪间距的目的。通过由3辆单元列车构成的虚拟编组列车的完整站间运行过程仿真结果以及与既有文献中类似方法的对比,证明本文所提出控制方法和优化算法的有效性。实验数据表明,分别与文献[8]的普通MPC方法以及基于文献[12]设计的RMPC方法相比,本文提出的RMPC控制方法及其优化算法可将单元列车追踪间距减小至5.05 m,缩短幅度达到分别达到49.5%和12.3%。

为简化算法设计,本文与文献[8]的处理方法一致,将单元列车之间的安全防护距离假设为固定的常数。在后续研究中,将考虑安全防护距离为非线性形式条件下的虚拟编组列车追踪控制方法。此外,列车动力学模型参数不确定条件下的控制方法设计问题也应在未来研究中进行考虑。