32 m简支梁桥有砟轨道精捣上拱误差模型及其修正研究

江来伟，岑敏仪，张同刚，李阳腾龙

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756；2.西南交通大学 土木工程学院，四川 成都 610031；3.成都理工大学 地球科学学院，四川 成都 610059)

轨道不平顺为轨道-车辆系统的激扰源,造成极大的机车车辆振动和轮轨作用力,对行车的安全性、舒适性、平稳性、机车车辆和轨道组件寿命以及环境噪声均产生很大影响[1-2]。张曙光等[3]对京津城际轨道平顺性研究时发现存在周期为33 m的高低不平顺,建议对周期性不平顺成因和控制方法进行深入研究。宋国华等[4]对秦沈线月牙河特大桥进行动力和轨道不平顺分析,认为桥上有砟轨道周期性高低不平顺并非由动荷载下桥梁挠度变形引起,根本原因是桥梁徐变引发上拱造成。陈宪麦等[5]对京沪、沪杭、沪宁等高速铁路轨道不平顺的研究表明,轨道高低普遍存在24～25 m、32～33 m不利波长范围的周期性不平顺。康熊等[6]分析高速铁路无砟轨道不平顺谱特征时发现,多等跨简支梁存在波长等于简支梁跨度的周期性不平顺。田国英[7]利用不平顺数据计算高速铁路轨道平均谱时指出,高低不平顺谱中包含大量的与桥梁跨距一致的波长成分。杨飞等[8]研究成灌城际铁路桥上动态检测高低数据时发现,存在周期性不平顺,认为混凝土的收缩、徐变以及桥梁刚度偏弱是主要原因,并指出32 m波长周期性不平顺落在列车160、200 km/h的敏感波长范围内。具有连续布置的多等跨简支梁桥的周期性变形,将改变轨道的几何状态,对列车的行车安全和乘坐舒适性均是有害的[9]。已有研究成果多针对无砟轨道动态检测高低不平顺进行分析,指出梁体上拱造成轨道高低周期性不平顺,并认为上拱是受混凝土徐变影响所致,但未就上拱数学表现形式及精测精调作业中如何科学地控制做进一步研究。目前桥梁有砟轨道精测精捣后普遍存在上拱问题,与无砟轨道相比,有砟轨道上拱机理研究较少。随着250 km/h有砟轨道运营线路越来越多,桥梁占比和大跨连续布置的多跨简支梁桥不断增加,为确保列车在有砟轨道桥梁段安全平稳地高速行驶,探究桥梁有砟轨道上拱成因和解决办法已迫在眉睫。

1 简支梁桥轨道垂向不平顺的动静态特性

轨道几何状态检测有静态检测(主要设备为各类轨测仪、电子水准仪等)和动态检测(主要设备为轨检车、动检车、综合检测列车等)。就垂向而言,静态检测获取轨道实测高程和设计高程,由二者代数差确定轨道垂向偏差,并可由此计算不同弦长的轨道高低[10]。动态检测是将轨道纵断面轨迹通过数字滤波运算,获得不同波长范围内的轨道高低。垂向偏差或不同波(弦)长高低用于描述轨道垂向不平顺。

已有研究表明[11],轨道长波不平顺可致使列车晃动、车体平稳性恶化、轨道形位劣化加速和车辆-轨道部件损伤。在高速条件下,轨道长波不平顺激励甚至会引发共振[12],威胁行车安全。以160 km/h为例,列车行驶时轨道高低的共振波长范围为31.4～62.8 m。若该波长范围内不平顺幅值较大,极易引起车体共振、车体平稳性恶化,故此需对30～70 m波长范围轨道高低不平顺进行合理控制[13-14]。

1.1 五种线下工程轨道高低不平顺谱

功率谱密度(Power Spectral Density,PSD)函数作为表征轨道不平顺的统计函数,能揭示随机变化的轨道不平顺幅值和波长两方面信息[11,14]。某设计速度160 km/h(预留200 km/h)电气化新建快速有砟铁路(部分隧道为无砟),统计里程K72+900—K220+900(上下行约296 km)范围内,联调联试80～160 km/h五种检测速度动态检测70 m截止波长轨道高低。按隧道洞口有砟轨道和无砟轨道过渡段,路基有砟轨道段,32 m简支梁桥(梁体为后张法预应力混凝土梁,下文相同)有砟轨道段,隧道有砟轨道和隧道无砟轨道段等五种线下工程区分。分别计算轨道高低平均不平顺谱,见图1。

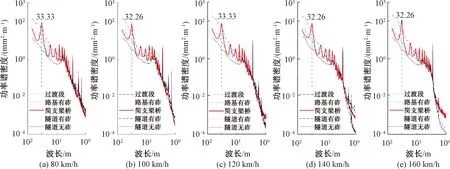
图1 五种线下工程轨道高低不平顺谱

不同速度等级下五种线下工程的轨道高低不平顺谱,其趋势基本保持一致,波长越长,高低不平顺幅值越大。但值得注意的是,32 m简支梁桥与其他线下工程存在显著差异,在波长3 m以上存在多个谱峰。其中,峰值处对应基频波,波长为32.26～33.33 m,这与32 m简支梁桥跨距基本吻合,其他谱峰多为倍频成分。不同线下工程的轨道高低不平顺谱表明,联调联试期间,32 m简支梁桥有砟轨道仍旧存在大量且波长单一的高低不平顺。

1.2 精捣前后轨道垂向不平顺的静态特性

有砟轨道的几何形位,主要由捣固车的精确捣固作业(以下简称精捣)来控制。精捣是依据静态检测横垂向偏差(精测)制定的精捣方案指导捣固车起/拨道抄平来实现的。受作业残余误差以及道床弹性不均的影响,有砟轨道精捣难以一次性完成。实际中采取“精测—精捣(稳)—精测”的重复作业模式(新建有砟铁路通常需3～4次精捣作业)[15],至各项指标符合静态验收标准后,实施联调联试作业。某新建有砟铁路由GPS/INS组合导航轨道快速检测系统配合DWL-48K型捣固车捣稳联合重复作业,捣固模式为三点式精捣。选取六座采用32 m后张法预应力混凝土梁布置的简支梁桥(a～f),最后三次(n-2、n-1、n)精捣后轨道静态检测垂向偏差(已做零均值化处理),得其波形见图2,n表示精捣作业的次数。计算3种弦长(10、30、70 m)的轨道高低不平顺,取200 m作为单元区段,统计最后两次精捣前后桥梁a～f区段平均标准差的变化,见图3。

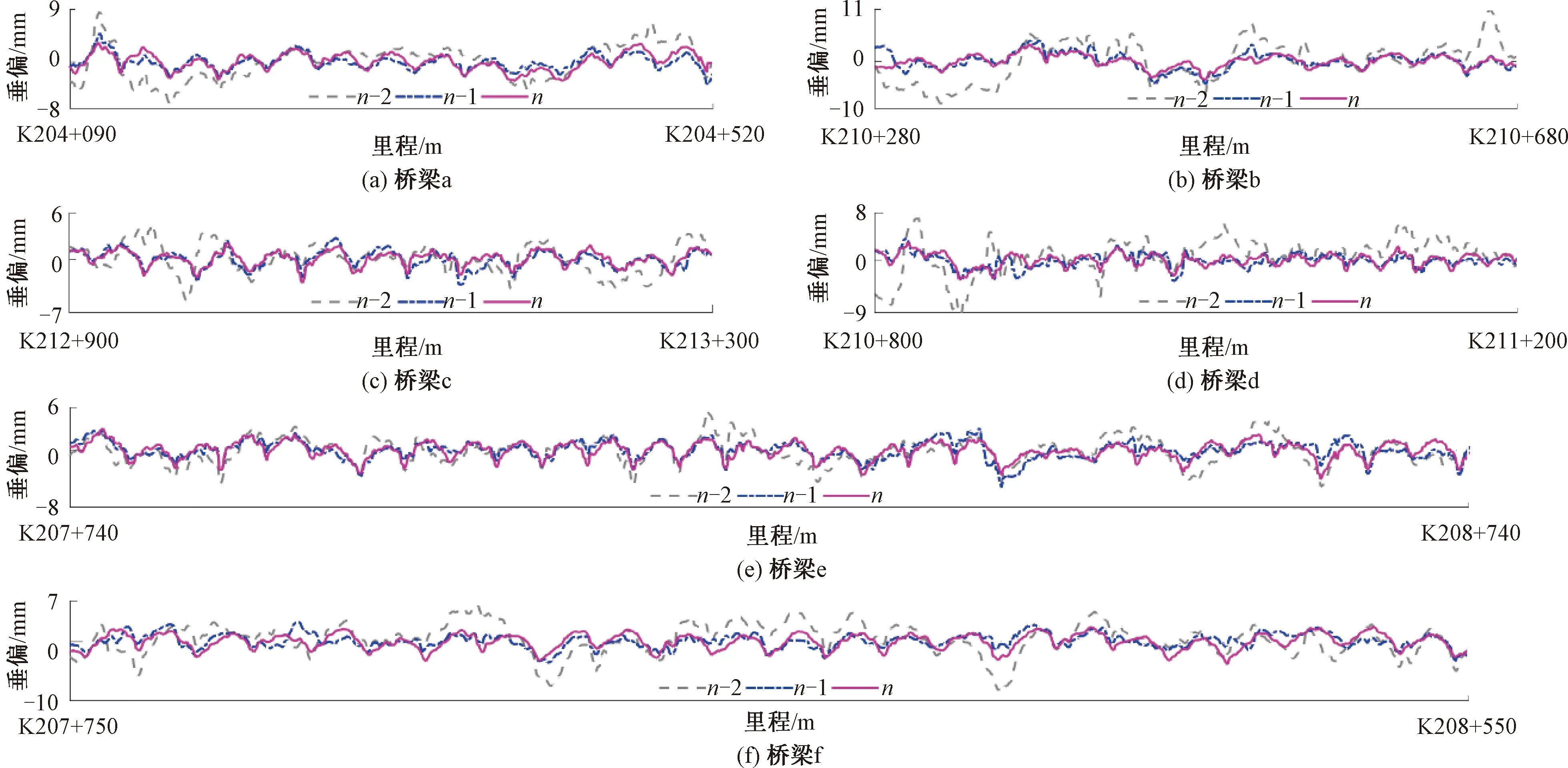
图2 多跨32 m简支梁桥有砟轨道最后三次精捣后垂向偏差变化

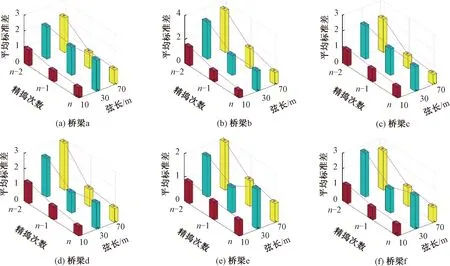
图3 最后三次精捣后不同弦长轨道高低的平均标准差变化

由图2垂向偏差波形变化知,n-1次较n-2次精捣后波幅显著减小,但n次(最后一次)较n-1次精捣后波幅变化微弱,且呈现出连续周期性上拱,波长固定为32.75 m,与32 m简支梁桥的跨距保持一致。根据图3可知,n-1次和n次精捣作业,弦长10、30、70 m的高低不平顺改善率[15]平均为30.1%、35.2%、55.3%和16.2%、-21.7%、21.9%。表明第n-1次精捣作业后,轨道3种弦长的高低均有显著提升,尤其是长弦70 m,其改善率高达55.3%。第n次精捣作业后,轨道10、70 m弦长的高低改善放缓,但30 m弦长对应的平均标准差较精捣前反而增加21.7%,且显著高于10、70 m弦长。综合来看,最后一次精捣作业起道抄平效果甚微,尤其精捣后30 m弦长的轨道高低不平顺不仅无改善,甚至有恶化之势。

尽管轨道初始形位各异,但经过重复的捣稳联合整道作业后,多跨32 m简支梁桥有砟轨道逐渐呈显著的周期性上拱形态,且通过增加捣固遍数亦难以将其消除。依据垂向偏差指导捣固车精捣作业,即使梁体存在徐变,垂向偏差中亦包含了徐变引发的上拱量。精捣后垂向偏差表明轨道上拱并未消除,此后起道抄平作业几乎再无效果可言。此外,梁体的混凝土徐变引发轨道上拱是一个缓慢、长期的过程[16],而有砟轨道精测精捣为短暂的持续作业行为。因此,简支梁桥有砟轨道精测精捣后上拱之成因与混凝土徐变关系不大。由于铁路简支梁桥整体结构多具有连续布置、多等跨的特点,致使精捣作业后各跨轨道呈周期性上拱。若轨道以桥梁跨距为波长的周期性上拱幅值过大,将造成轨道垂向连续多(长)波不平顺。这不仅会使以100 ～200 km/h速度开行的车辆的车体平稳性恶化,轨道形位劣化加速及车辆-轨道部件损伤,甚至可能激励列车产生车-桥共振。因此,迫切需要探究梁上有砟轨道精捣后上拱的成因和解决办法,以便有效地控制或减弱其影响,确保列车在桥上安全平稳地行驶。

2 捣固车起道抄平误差模型及静态修正

轨道垂向不平顺整正包括纵向矢距(以下简称矢距)检测和起道抄平,起道抄平采用三点(R、M、F)式精捣控制[17],见图4。R、F间张紧一根钢绳作为捣固车矢距检测的基准弦(图中红色虚线),R位于已整修完毕(精捣后)的轨道上,F位于未整修(精捣前)的轨道上。M为起道抄平、捣固作业点,该点装有矢距传感器。依据M处轨道矢距HM(由于矢距远远小于基准弦长度,矢距近似为图中HM,并定义基准弦偏下为负),mm,即可实现自动起道抄平作业(近似捣固)。近似捣固依靠长度为RF的基准弦对轨道进行平滑整正,本质为低通滤波。实际上,受基准弦长度的限制,近似捣固难以消除超过基准弦长的轨道中长波不平顺。若预先由精测获得基准弦前端F处的轨道垂向偏差vF,则三点式精捣M处轨道的理论起道量lM为

图4 纵向起道抄平误差

( 1 )

式中:a为RM的长度;b为MF的长度;ζ为预留量(预留量是指轨道设计高程面与精捣后实际高程面之间的高差),mm。

将作业段内各点里程、垂向偏差和预留量作为精捣方案输入车载ALC计算机,ALC自动计算各点起道量并实施起道抄平、捣固作业,以此实现轨道垂向不平顺的控制。

2.1 捣固车起道抄平误差模型

捣固作业中除车辆荷载以外,捣固装置还向道床传递巨大挤压力。受捣固车动荷载影响,梁体受挤压力而处于下弯变形状态,轨道垂向状态由1变为1′,见图4。此时,M处轨道实际矢距变为H′M,则M处轨道的实际起道量为

( 2 )

结合式( 1 ),并考虑-H′M>-HM,推得捣固车在桥梁各跨精捣作业时,实际起道量大于理论起道量,并与作业点矢距的变化直接相关。捣固车荷载与挤压力消失后,梁体恢复至恒载状态,轨道随梁体回弹产生垂向不平顺,最终表现为自梁端至跨中逐渐向上弯拱,即轨道上拱,见图4。捣固车动荷载作用下的梁体挠度变形致使捣固车起道抄平产生误差,则M处起道抄平误差eM为

eM=l′M-lM=-H′M+HM

( 3 )

进一步可得,在桥梁任意里程k处,捣固车起道抄平误差模型(Lifting and Levelling Error Model,LLEM)的一般表达式为

ek=l′k-lk=-H′k+Hk

( 4 )

式中:lk、l′k分别为里程k处的理论起道量和实际起道量;Hk为里程k处轨道矢距,H′k为里程k处捣固车动荷载作用下的轨道矢距。

综上所述,轨道上拱是捣固作业点实际矢距发生变化引入起道抄平误差所致,是作业中梁体受捣固车动荷载作用的表现结果。为控制轨道上拱,需对输入车载ALC计算机的轨道垂向偏差做修正处理,以消除捣固车起道抄平作业中的这一系统误差。因此,探究轨道上拱的数学表现形式是解决问题的关键。

2.2 垂向偏差的静态修正函数

因轨道上拱是以桥梁跨距为波长的垂向不平顺,需滤除轨道垂向偏差中波长较短(由擦伤、焊缝、波磨、新轨辊式矫直或检测精度等造成的短波垂向不平顺)和较长(如静态检测累积误差或捣固车未消除的大于跨距的长波垂向不平顺)的成分,即滤除垂向偏差中高频扰动和低频趋势项[18]。对最后一次精捣后的轨道垂向偏差作带通滤波处理,波长设置为5～35 m。 图5为总长为L的多跨32 m简支梁桥有砟轨道垂向偏差带通滤波前后示意。

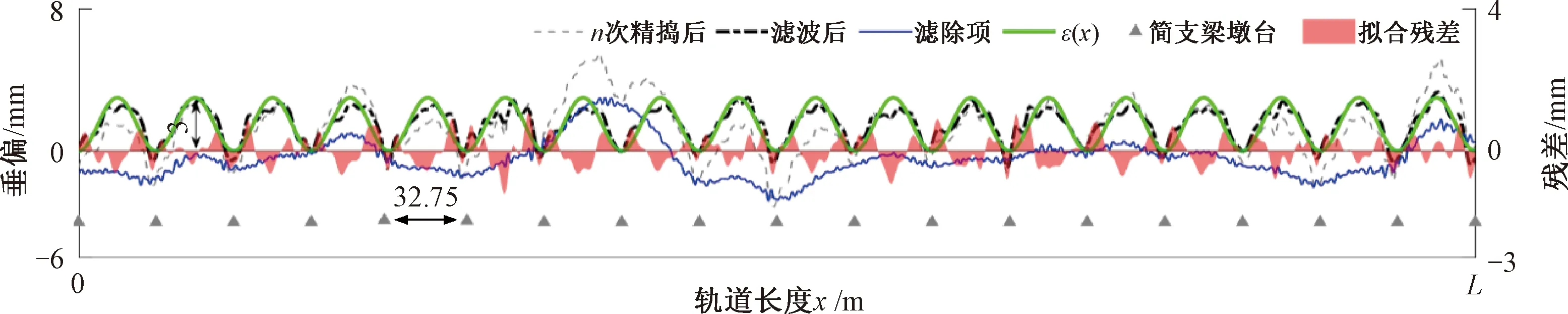
图5 多跨32m简支梁桥有砟轨道垂向偏差带通滤波及上拱拟合示意

滤除垂向偏差中高频扰动和低频的大幅度趋势项后,垂向偏差数据更加中心化,轨道上拱特性更为显著。滤波后的垂向偏差表明精捣后轨道呈周期性上拱,上拱的波长固定为32.75 m,与32 m简支梁跨距保持一致,波谷对应简支梁墩台处,波峰对应于跨中。考虑滤波后垂向偏差数据规律变化的特点,以简支梁跨距为周期的正弦函数作为目标函数,依据最小二乘作曲线拟合。拟合残差见图5,以整体拟合残差的均方根误差最小为准则,得轨道上拱的最优拟合函数为

x∈[0,32.75]

( 5 )

式中:x为自32 m简支梁前端起始墩台中心沿轨道的长度,m。

由ε(x)知,轨道上拱最大幅度约为3 mm,位于跨中,见图5。梁上轨道上拱是捣固车起道抄平误差的表现形式。那么ε(x)则为描述起道抄平误差ek的数学模型,又称为垂向偏差的静态修正函数。若桥梁里程k处轨道垂向偏差为vk,则静态修正后的轨道垂向偏差vSCk为

vSCk=vk+ε(x)=vk+ε(k-k0)

( 6 )

式中:k0为距离里程k处最近的小里程端墩台中心里程。

将k、vSCk和ζ输入至车载ALC计算机,ALC依据式( 2 )即可计算各跨轨道经过静态修正后的起道量。式( 6 )为顾及捣固车起道抄平作业中的系统误差,通过静态修正函数ε(x)的补偿,实现减弱或消除梁体上轨道上拱。

3 轨道预拱模型及动态修正

静态检测为轨道荷载忽略不计的轨道几何形位测量,动态检测则为拟真测试。动态检测时轨道几何形位更加接近列车运行时的真实状态,但精捣方案是依据静态检测数据计算确定的。为提高列车在32 m简支梁桥有砟轨道的动态平顺性,精捣作业时应顾及简支梁桥轨道动静态垂向不平顺的差异。动态检测得到的是惯性基准下一定截止波长的轨道不平顺数据,静态检测获得的是几何基准下轨道的横垂向偏差。动态检测里程误差远大于静态检测的,两者数据无法直接比较,需作数据预处理[18],主要包括动态检测里程误差修正(统一里程)和动静态检测截止波长35 m的高通滤波处理(统一波长)。动静态检测轨道垂向波形在里程上并不吻合,但相邻墩台间均有上拱特性。利用这一特性,对动态检测里程作局部修正处理,便可解决动静态检测波形错位的问题。里程误差修正主要有最小二乘法、相关系数法[19]。鉴于静态检测里程误差极小,把静态检测垂向偏差所确定的墩台位置作为校正点,采用基于局部波形匹配的方法修正动态检测里程误差,见图6。

图6 里程修正前后的动静态检测轨道垂向波形示意

经动态检测里程误差修正和动静态检测高通滤波处理,动静态检测轨道垂向波形在里程与波长上实现统一。图7为总长为L的多跨32 m简支梁桥,预处理后的动静态检测轨道垂向波形及互差示意。

图7 多跨32 m简支梁桥有砟轨道动静态检测垂向波形及互差示意

由图7所示波形可知,多跨32 m简支梁桥有砟轨道动静态检测垂向不平顺互差同样呈现以跨距为波长的周期性变化,且自各梁端支点处至跨中逐渐增大,但在隧道洞口的无砟轨道与有砟轨道过渡段、有砟轨道路基段、有砟轨道或无砟轨道隧道段均未有类似的规律性存在。鉴于动态检测时,轨道垂向状态更加接近列车运行时的状态,精捣作业中,若依据动静态检测各跨垂向不平顺的互差规律,为简支梁桥有砟轨道预设合理的上拱量,将有利于改善高速列车通过时垂向的动态平顺性。

控制梁体上有砟轨道的预拱,预拱量的确定是关键。同样考虑互差数据呈周期性变化的特点,以跨距为周期的正弦函数作为目标函数,采用最小二乘曲线拟合,拟合残差见图7。以整体拟合残差的均方根误差最小为准则,得32 m简支梁桥有砟轨道预拱模型(Ballasted Track Pre-camber Setting Model,BTPCM)为

x∈[0,32.75]

( 7 )

由η(x)可知,32 m简支梁桥有砟轨道动静态检测垂向互差最大约为1 mm,同样位于跨中,见图7。依据BTPCM,对式( 6 )所得的静态检测垂向偏差进行修正,即

vDCk=vSCk-η(x)=vk+ε(k-k0)-η(k-k0)

( 8 )

式中:η(k-k0)为依据BTPCM确定的32 m简支梁桥有砟轨道精捣预拱量。

式( 8 )所得垂向偏差vDCk是在补偿捣固车纵向抄平误差,同时依据BTPCM为梁上有砟轨道设置预拱量,以提高32 m简支梁桥有砟轨道垂向的动态平顺性。设置预拱的轨道,其10 m弦最大矢距约±0.2 mm,30 m弦最大矢距约±0.98 mm。据此,建议有砟轨道静态验收时,10 m和30 m弦高低容许偏差应顾及桥梁段预设上拱量的这一特性。

4 模型验证与探讨

为检验起道抄平误差模型和有砟轨道预拱模型的有效性,在某新建铁路线路有砟轨道上由GPS/INS组合导航轨道快速检测系统配合DWL-48K型捣固车做精测精捣工程试践验证。工程试验段有多跨32 m简支梁桥16座,桥梁占比约为24%。图8为某长为1.2 km(K143+300—K144+500)的多跨32 m简支梁桥段,工程试验后的动静态检测轨道垂向不平顺和车体垂向加速度波形示意。图8所示为墩台号1～13范围内静态修正区段,起道量计算仅采用静态修正函数来补偿起道抄平误差;墩台号13～25范围内为动静态修正区段,起道量顾及LLEM和BTPCM联合计算,补偿起道抄平误差的同时设置轨道预拱量;墩台号25～37范围内为未修正区段,起道量由静态检测垂向偏差直接确定,即不作起道抄平误差和轨道预拱量修正。图8数据来源:n次精捣前、后的垂向偏差由静态检测精测确定,高低为动态检测长波通道输出值,车体垂向加速度为动态检测车20 Hz的低通滤波输出值。

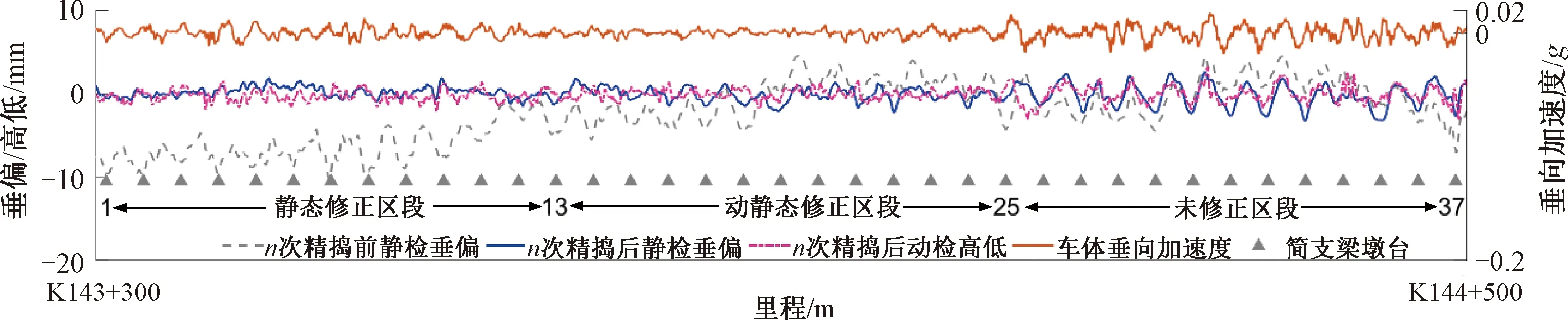
图8 多跨32m简支梁桥轨道垂向不平顺及车体垂向加速度波形示意

从静态检测垂向偏差波形来看,捣固车n次精捣作业后,轨道垂向平顺性,静态修正区段优于动静态修正区段;从动态检测高低波形来看,轨道垂向平顺性,动静态修正区段却优于静态修正区段;但不论是静态检测垂向偏差亦或动态检测高低波形,未修正区段各跨有砟轨道精捣后仍旧呈显著的周期性上拱。至于车体垂向加速度波形,动静态修正区段加速度的波动最为平缓,静态修正区段次之,而在未修正区段简支梁墩台处和跨中,出现大量的垂向加速度峰值。

为具体对比和显示动静态修正对轨道垂向平顺性控制的效果,从最后一次精捣前后静态检测垂向偏差三种弦长对应的平均标准差、动态检测高低不平顺PSD、车体垂向加速度分布三个方面进行对比分析,见图9。

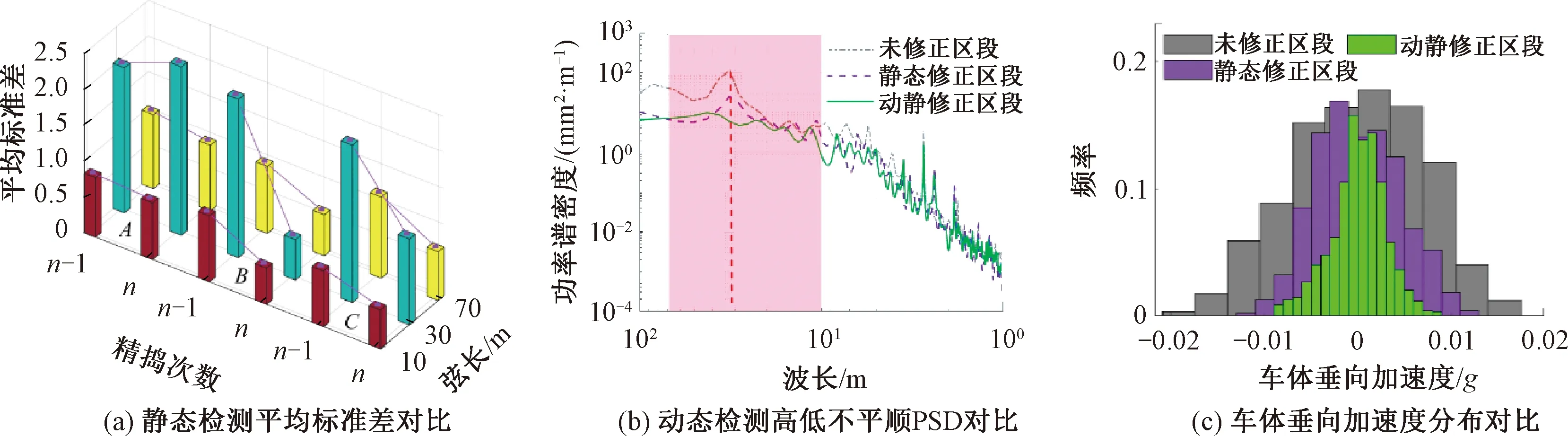
图9 轨道垂向平顺性控制对比

图9(a)中,A为未修正区段,B为静态修正区段,C为动静态修正区段。第n次精捣作业后,三个区段各弦长(10、30、70 m)的轨道高低不平顺改善率分别为4.8%、-16%、10.9%,45.1%、74.4%、38.7%和29.7%、45.4%、39.8%,表明B、C区段三种弦长下轨道高低不平顺得到极大改善,尤其30 m弦长改善74.4%和45.4%最为显著,这是因为有砟轨道上拱得到有效减弱或消除。n次精捣后,10 m弦和70 m弦对应的平均标准差,C区段略高于B区段;30 m弦对应的平均标准差,C区段明显高于B区段,表明简支梁桥精捣中仅补偿起道抄平误差,能有效地减弱或消除有砟轨道上拱,获得更优的静态垂向平顺性。

由图9(b)中动态检测不平顺PSD曲线,未修正区段包含大量以32 m简支梁桥的跨距为波长的周期性不平顺。静态修正区段,尽管图9(a)表明已消除了各跨轨道上拱,但动态检测高低显示,仍旧会出现一定幅度的以简支梁桥跨距为波长的周期性不平顺。动静态联合修正区段,几乎完全消除了这种周期性不平顺,表明简支梁桥有砟轨道精捣中补偿起道抄平误差的同时,设置预拱量可获得更优的动态垂向平顺性。

根据图9(c)统计结果,未修正区段、静态修正区段和动静态修正区段车体垂向加速度均值约为0,标准差约为0.007g、0.004 5g和0.003g。表明采用动静态联合修正,轨道精捣后的车体垂向动力响应最小,舒适性最优,具有更高的动态垂向平顺性。

新建铁路有砟轨道线路精测精捣工程实践验证了LLEM和BTPCM在减弱或消除32 m简支梁桥有砟轨道精捣后上拱的有效性。换而言之,就有砟轨道平顺性而言,精测精捣中补偿起道抄平误差的同时设置预拱量,能够切实有效地提高梁体上有砟轨道的动态垂向平顺性。

5 结论

大量的桥梁有砟轨道精测精捣实践显示,垂向不平顺表现出不同于其他线下工程的上拱特性。研究桥梁有砟轨道精测精捣后上拱的成因,及32 m简支梁动静态修正模型LLEM和BTPCM,经工程实践验证正确有效,得出以下主要结论:

(1)有砟轨道桥梁段存在精捣作业难以消除的轨道上拱,造成多跨桥梁轨道垂向多(长)波不平顺。轨道上拱是因捣固作业点矢距发生变化引入起道抄平误差所致,是作业中梁体受捣固车动荷载影响的结果。32 m简支梁桥有砟轨道精捣后静态垂向不平顺幅值在跨中达3 mm,波长固定为32.75 m。

(2)桥梁有砟轨道精捣后,梁上静态检测与动态检测的轨道垂向不平顺幅值不相等,其垂向不平顺互差自梁端至跨中逐渐增大。32 m简支梁桥有砟轨道在跨中的动静态垂向不平顺互差可达1 mm,波长固定为32.75 m。

(3)32 m简支梁桥有砟轨道精测精捣中,采用起道抄平误差模型(LLEM)能消除或减弱轨道上拱,进而有效地控制梁上轨道静态垂向长波不平顺;精测精捣中补偿起道抄平误差并顾及有砟轨道预拱模型(BTPCM),更能有效提高32 m简支梁桥有砟轨道动态垂向平顺性。

(4)有砟轨道静态验收时,经LLEM和BTPCM联合修正后的32 m简支梁桥段,应与其他线下工程区分开来,垂向不平顺容许偏差的管理值应顾及梁上有砟轨道预拱量。

高速铁路有砟轨道的大量建设,以及新建铁路桥梁占比和多等跨简支梁桥的不断增加,使得科学有效地控制桥上有砟轨道的动态不平顺,兼具科学理论意义和工程实用价值。本文研究结论不仅适用于32 m跨简支梁桥有砟轨道精测精捣,对其他类型或跨距桥梁的有砟轨道精测精捣及其相关技术标准的制定也有参考价值。