基于货-车-轨耦合动力学分析的重车重心高度及管控规则研究

杨能普，周 苗，王文昆，黄 全，韩 梅

(1.湖南工业大学 轨道交通学院，湖南 株洲 412007；2.株洲时代电子技术有限公司，湖南 株洲 412007；3.中国铁路广州局集团有限公司，广东 广州 510088；4.北京交通大学 交通运输学院，北京 100044)

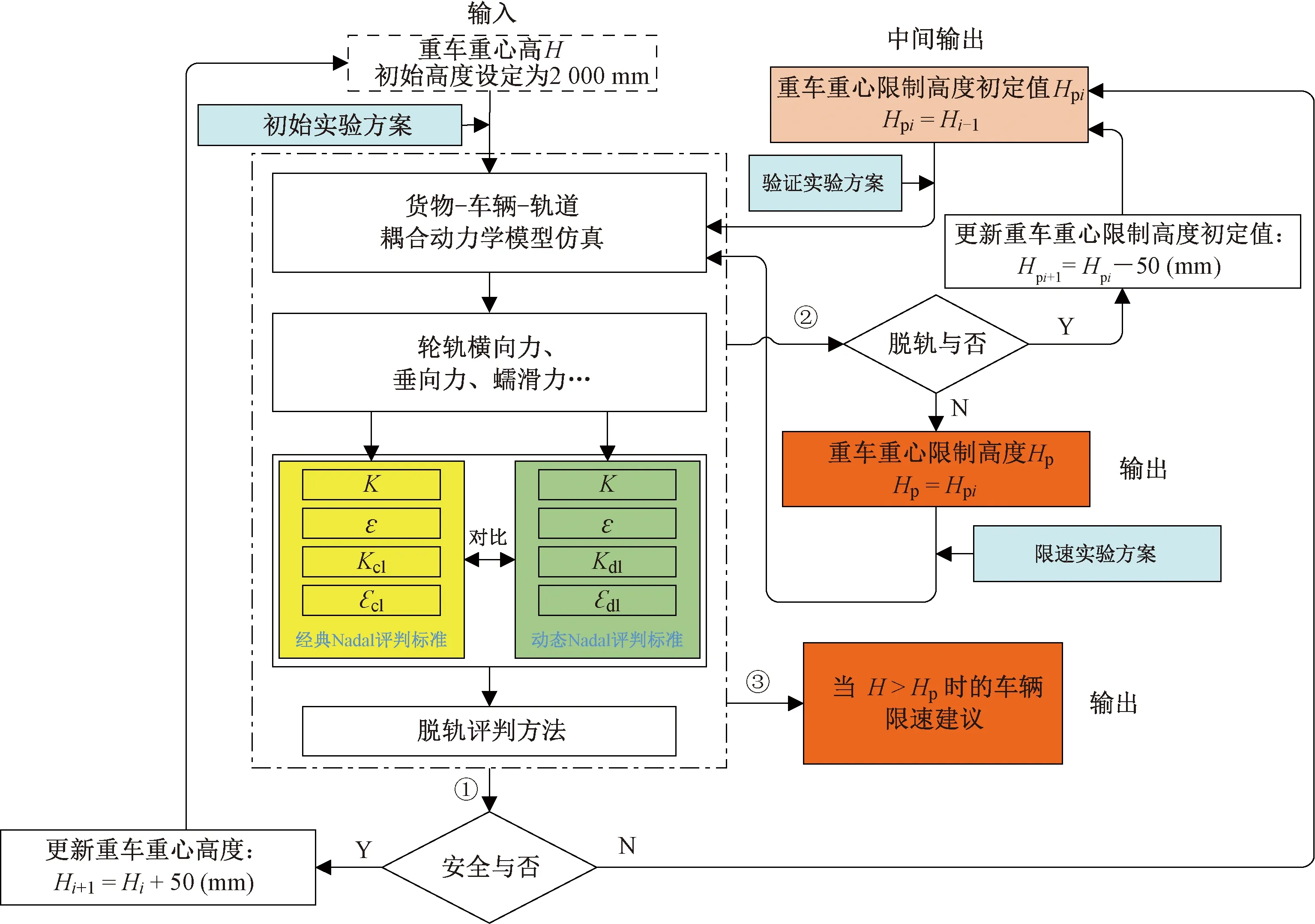
近年来随着重载提速战略的推动,我国铁路线路、车辆性能等硬件条件已大幅改善;但在铁路货运管理中,我国现行的重车重心高度管控规则仍沿用几十年前的管理规定:重车重心高度H不超过2 000 mm,铁路通用货车方可按正常速度运行;当2 000 mm

早期针对这一问题的研究,主要采用静力学建模和调研统计分析方法。部分研究通过构建重车重心高度影响脱轨系数、轮重减载率、倾覆系数等车辆运行安全指标的静力学模型进行理论计算,提出我国铁路通用货车重车重心限制高度可提升至2 200～2 400 mm[8-11]。文献[12-14]通过调研运输实例、统计分析车辆动力学试验结果等方式,指出我国通用货车重车重心限制高度可适当提升。近年来,随着计算机仿真技术发展,大量研究者开始采用虚拟样机建模开展仿真实验,探讨铁路通用货车重车重心高度管控规则的合理优化。文献[15-16]采用SIMPACK动力学仿真计算,提出双层集装箱车、C62BK型敞车的重车重心限制高度可达2 480、2 400 mm。文献[17-24]采用SIMPACK、ADAMS/Rail、VAMPIRE等动力学软件,对货物重心参数(包含重车重心高度)影响车辆运行安全展开了相关的研究。

上述研究从不同方面探讨了重车重心高度对车辆运行安全指标的影响,推动了重车重心高度管理规则的合理优化。然而这些研究仍存在一些不足:

(1)所构建的货物-车辆-轨道耦合动力学模型,对货物-车体耦合效应的细观机理研究较少,一般采用货物参数叠加或引入线性力元方式简化处理货物-车体耦合作用,对货物采用柔性加固的松弛失效、不同预紧力下呈不同交变拉力规律等非线性力学效应考虑较少,模型精度仍有待提升。

(2)主要采用经典Nadal限度评判车辆的脱轨风险,评判精度有待提升;经典Nadal限度在评判精度上存在一定局限[25-26],较难适用于“货物参数”此类影响车辆运行安全显著性不高、需要高精度评判方法的场景。

(3)缺乏较为科学系统的实验方案设计,一般均是基于经验列举工况,因此很难确保所提出的管控约束规则适应所有工况的运行安全性。

(4)主要关注重车重心合理限制高度,对于重心超过限制高度后的车辆运行限速规则研究尚属空白。

为此,本文针对上述问题,构建更为精细化的货物-车辆-轨道耦合动力学模型,对铁路通用货车重车重心高度管控规则的优化重构展开研究。通过深入分析货物加固于车体的非线性力学作用效应,揭示货物-车体耦合机理,建立货物-车辆-轨道耦合动力学模型;通过引入轮轨蠕滑力约束机制,推导动态Nadal限度,有效降低脱轨误判率,提高脱轨风险评判准确性;基于前期研究得到的最不利工况[27],设计重车重心高度管理规则优化探索的实验方案;最后根据实验方案开展仿真实验研究,并以动态Nadal限度评判车辆脱轨风险,分析实验结果,提出我国铁路通用货车的重车重心限制高度以及重心超高时限速规定的规则建议。

1 货物-车辆-轨道耦合动力学模型

常规车辆-轨道耦合动力学建模分析中,货物重量往往只是叠加至车体或被忽视,因而重车重心位置与车体几何中心位置一致。然而,货物质量不一定均质,货物重心还可能偏移车体中心进行装载,此外车辆运行中货物受加固力牵引还可能移位等,这些均会导致考虑货物耦合效应的货物-车辆-轨道系统,与常规车辆-轨道耦合模型相比,在动力学行为上有所差异。因此,深入分析货物-车体耦合的细观机理,拓展车辆-轨道耦合动力学模型是十分必要的。

在建模时,车辆-轨道系统采用广泛应用的翟模型[28],但针对车体动力学方程需考虑货物加固力耦合影响作出修正,重点集中于建立货物振动方程组,并考虑其与车体的耦合。为便于阐述,此处采用货物加固中典型的拉牵加固方式加以说明。图1为货物-车体子系统拉牵加固形式、受力分析及力学耦合机理,表1列出了建立此子模型的一般参数。

图1 货物-车体子系统力学分析及耦合机制

表1 一般参数定义

根据如图1所示的货物-车体子系统力学耦合机理进行分析,基于达朗贝尔原理[28],得到货物的横摆运动方程为

( 1 )

考虑力的空间几何分解及胡克定律,货物拉牵力Fhci沿y轴的分力Fyhci为

( 2 )

考虑库仑摩擦定律,货物-车体间沿y轴的摩擦力Fych可表示为

( 3 )

将式( 2 )、式( 3 )中的Fych、Fyhci代入式( 1 ),货物横摆方程等价转化为系统随机振动的一般形式为

( 4 )

同理,货物的其他振动模态动力学方程可以表示为

zh·cosω=μhcMhgcosω

( 5 )

( 6 )

( 7 )

( 8 )

( 9 )

式( 4 )～式( 9 )组成的方程组构成货物子系统动力学模型。此外,考虑货物拉牵绳拉力的耦合作用,对经典翟模型中的车体动力学方程组进行修正。在此基础上,式( 4 )～式( 9 )与修正翟模型构成的动力学方程集,即为新构建的货物-车辆-轨道耦合动力学模型。根据扩展得到的动力学方程集,利用SIMPACK动力学软件平台,构建相应的货物-车辆-轨道系统多体动力学虚拟样机模型,如图2所示。该模型有效处理了货物-车辆的耦合,将被用于后续深入探讨重车重心高度对铁路货车运行安全的影响,优化重构重车重心高度的管控规则。

图2 货物-车辆-轨道系统多体动力学虚拟样机模型

2 车辆运行安全评估方法

相较于车辆性能、线路工况、运行速度等因素,重车重心高度对车辆运行安全的影响显著度相对更小,致使采用经典Nadal脱轨评判方法难以精确研判铁路货车的脱轨风险。因而从轮轨蠕滑接触特性分析出发,对经典Nadal脱轨限值作出修正,提出一个动态Nadal评判标准,对于提高脱轨评判准确性、更好界定重车重心高度约束规则显得尤为重要。为此,首先对轮轨接触受力展开分析,如图3所示。

图3 轮轨接触的力学分析

图3中,Trx、Tlx、Try、Tly、Nr、Nl分别为接触点坐标系中左右两轮的纵向、横向蠕滑力及法向力;Q1、Q2、P1、P2分别为轨道坐标系中左右两轮接触点处的横向力、垂向力;Fy、W分别为轮对横向力、垂向力;α为轮缘接触角。

为求得车轮脱轨系数的极限,首先对轮缘接触侧的空间受力特性进行分析。通过坐标变换分析,各力之间的关系可表示为

Q1=Nrsinα-Trycosα=Nrsinα-μeNrcosα

(10)

P1=Nrcosα+Trysinα=Nrcosα+μeNrsinα

(11)

式中:μe为实际有效摩擦系数,μe=Try/Nr[29]。

根据式(10)、式(11),可得

(12)

(13)

车辆运行过程中,轮轨蠕滑力呈现如图4(μ为库伦摩擦系数)所示的特性[30]。

图4 轮轨蠕滑特性

根据该特性,轮轨蠕滑力约束机制可表示为

(14)

(15)

联立式(13)和式(15),可得实际有效摩擦系数μe的约束表达式为

(16)

将式(16)中μe的上限代入式(12),同时考虑脱轨临界状态下的α达到最大轮缘角αmax,得到脱轨系数动态限度Kdl为

(17)

由图4可知,大多数情况下μe≤μ,故大部分情形下Klimit(αmax,μe)≥Klimit(αmax,μ),Klimit为极限状态下脱轨系数。经典Nadal限度Kcl中采用库伦摩擦系数μ计算得到固定限度值评判车辆是否脱轨,会导致α尚未达到最大轮缘角αmax就被判定为脱轨,出现误判。而采用式(17)所示的脱轨系数动态限度Kdl,因采用实际有效摩擦系数μe上限值替代库伦摩擦系数μ,即可避免这一问题,有效减小脱轨误判率[31]。

同理分析踏面接触侧车轮的受力情况,结合轮重减载率限值与脱轨系数限值的关系[32],得到轮重减载率动态限度εdl为

(18)

Kdl、εdl引入轮轨蠕滑力约束机制,通过采集实时的轮轨接触力,对经典Nadal脱轨限度公式进行修正,得到新的车辆脱轨评判动态限度值,避免了α尚未达到最大轮缘角αmax就判定脱轨的情况,有效降低了脱轨评判的误判率;两者被统称为动态Nadal限度,用于评判本文各实验方案的车辆运行安全[33-35],即

K=Q/P≤Kdl

(19)

ε=|(P2-P)/(P2+P1)|≤εdl

(20)

式中:K为脱轨系数;Q、P分别为轮轨接触点横向力、垂向力;ε为轮重减载率。

3 实验方案设计

基于木桶定律(Cannikin Law)[36-37]可知,铁路货车若能通过最不利工况实验方案及实验流程下的安全性测试,即能确保优化重构的重车重心高度管控规则,满足所有工况条件下的运行安全需求。为此,设计如图5所示的实验流程,图5中序号①、②、③表示实验分步进行。初始实验方案、验证实验方案及限速实验方案见表2,其中,初始实验方案采用文献[7,27]确定的最不利工况,验证实验方案、限速实验方案通过放宽相关因素水平而设计。

图5 动力学仿真实验流程

表2 实验方案

4 仿真结果分析与讨论

根据图5所示的实验流程,基于前文所构建的货物-车辆-轨道系统多体动力学虚拟样机模型,对最不利工况实验方案中的车辆是否存在脱轨风险展开仿真计算分析(图5中,Hpi为重车重心限制高度初定值,Hp为重车重心限制高度)。模型计算中,分别选择AAR5级谱、AAR3级谱作为我国Ⅰ级线路、Ⅲ级线路的轨道不平顺激励;所有工况均采集Ⅰ位轮对的数据进行分析;结果文件后处理中,采用低通滤波方式,截止频率设为20 Hz。

Step1采用经典Nadal限度和动态Nadal限度分别对铁路货车的运行安全进行评估,仿真结果如图6所示。

由图6可知,经典Nadal限度采用一个固定值评估车辆运行安全,导致一定程度的脱轨误判,而动态Nadal限度会根据列车运行在线路上具体位置的实时轮轨接触状态,动态实时地计算安全限值,评判车辆是否安全,有效降低了脱轨误判率。相比而言,采用动态Nadal限度评判车辆脱轨风险更为精确可靠,更适宜用于铁路通用货车重车重心高度管控规则的优化重构研究。因此,在后续的仿真结果分析中,均采用动态Nadal限度作为车辆脱轨评估方法。

此外,根据图6的评估结果进行分析,可知采用动态Nadal限度作为评估方法,当重车重心高度为2 400 mm时,铁路通用货车可以通过最不利工况实验方案下的安全性测试;当重车重心高度为2 450 mm时,最不利工况2条件下的轮重减载率超过其动态限度;因此,可初步确定重车重心限制高度初定值Hpi设置为2 400 mm,得到中间输出,实验进程进入下一步环节。

Step2按照表2中的验证实验方案开展仿真实验,仿真结果如图7所示。从图7可以看出,当重车重心高度为2 400 mm时,安全指标均低于动态Nadal限度,车辆可以通过验证实验的运行安全性测试。因此,可建议重车重心限制高度Hp取初定值Hpi(2 400 mm),该值接近ATSB标准的2 500 mm、AAR标准的98 in(2 489.2 mm),略高于UIC标准的2 300 mm[3-5]。

图7 重车重心高度为2 400 mm的车辆脱轨风险分析

Step3按照表2中的限速实验方案,设定重车重心高度水平分别为2 500,2 600,…,3 000 mm,开展重车重心超高后的区间限速实验。分析实验结果,得各水平等级下的区间限速条件见表3。此处为节省篇幅,仅展示重车重心高度为3 000 mm时的仿真结果,如图8所示。

图8 重车重心高度为3 000 mm的车辆限速条件仿真分析

表3 重心高度超过2 400 mm时的车辆速度限速建议值

根据表3所示的实验结果,对重车重心高度管控规则展开进一步的探讨。考虑铁路货运作业的可操作性,基于“木桶定律”逻辑,本文建议铁路通用货车重车重心高度超过2 400 mm后的限速管控规则为:当2 400 mm

表4 现行规则与建议规则对比

5 结论

针对现行重车重心高度管控规则限制货运系统运力的问题,本文在分析货物-车辆耦合机理的基础上,对车辆-轨道耦合动力学模型进行扩展,建立货物-车辆-轨道耦合动力学模型;根据轮轨蠕滑力约束机制,提出动态Nadal限度脱轨风险评判方法;利用最不利工况,设计优化重车重心高度规则的实验流程及相应的实验方案;最后基于模型、实验方案及脱轨评估方法,通过SIMPACK动力学仿真对重车重心高度影响车辆运行安全的行为进行研究,提出一个新的、更为合理的铁路通用货车重车重心高度建议约束规则。主要结论如下:

(1)本文构建的货物-车辆-轨道耦合动力学模型,科学地考虑了货物的耦合机制,与传统模型相比,该模型能更准确地分析货物装载参数对铁路货车运行安全性的影响。

(2)本文推导的动态Nadal限度通过引入轮轨蠕滑力约束机制,避免了轮缘角α未达到最大轮缘角αmax就被判定为脱轨的情形;相较于经典Nadal限度,有效减小了脱轨误判率,更适宜作为铁路车辆脱轨风险评估的评判依据。

(3)基于前期研究所获得的最不利工况及木桶定律,设计了较为合理的实验流程及其实验方案,相较于根据经验列举工况的实验设计方式,可更全面地考虑车辆类型、运行速度、装载条件、轨道条件等因素处于不同水平相互交织耦合所形成的复杂服役工况。

(4)基于动态Nadal限度脱轨评判方法,评估测试各实验方案的车辆运行安全性;通过实验结果的分析,得到重车重心高度建议管控规则:重车重心高度H不超过2 400 mm,铁路通用货车可按正常速度运行;当2 400 mm

需要说明的是,本文所提的重车重心高度管控规则目前只适用于铁路通用货车;对于凹底平车、落下孔车、钳夹车等专用货车装运重型机械、大型变压器等情形,仍需作进一步探索。本文所提方法目前只适用于稳态爬轨脱轨过程的分析,针对瞬态跳轨脱轨过程仍不适用。此外,本文研究结果需组织线路实验,结合GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》标准作进一步的对比考核验证。