利用数形结合方法求解对数函数问题
刘 举
(吉林省长春吉大附中实验学校)
数形结合能将数学的符号语言和图形语言相互转化,能让解题者实现抽象思维与形象思维的对接,从而参透数学问题的本质.它具有灵活性、形象性、直观性等特点,是数学解题最基本的思想方法之一.
1 判断函数零点个数
对于与对数函数有关的函数零点问题,若难以直接求出零点,则可考虑将原问题转化为函数图像的交点问题,通过对数函数的图像和其他初等函数的图像的交点个数来判断原函数零点的个数.
例1已知函数f(x)=2cos(ωx+φ)(ω>0,0<φ<)的部分图像如图1所示,g(x)=f(x)-log2x,则g(x)的零点个数为_________.
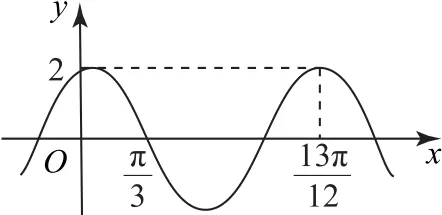
图1
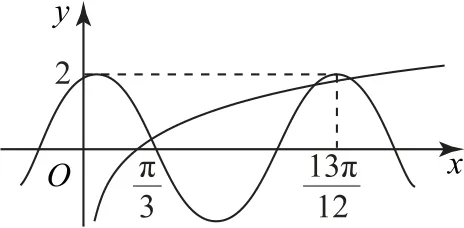
图2
点评本题将一个函数的零点问题转化为两个函数图像的交点问题,充分体现了函数与方程的关系,同时也为确定超越方程的根的个数问题提供了一种切实可行的方法.
2 处理有关不等式问题
对于非常规的不等式问题,一般有两种思路:一是通过恒等变形将原不等式转化为常规不等式,再用常规方法来解;二是当无法将原不等式转化为常规不等式时,可借助函数图像将原不等式转化为两个函数图像之间的位置关系,从而借助图像分析得到答案.
例2(1)已知函数f(x)=log2(x+1),则不等式f(x)>|x|的解集是________;
(2)若不等式(x-1)2<logax(a>0,且a≠1)在x∈(1,2]内恒成立,则实数a的取值范围为( ).
解析(1)作出函数y=log2(x+1)和y=|x|的图像,如图3 所示,两个函数的图像相交于点(0,0)和(1,1),当且仅当x∈(0,1)时,y=log2(x+1)的图像在y=|x|的图像的上方,即不等式f(x)>|x|的解集为(0,1).
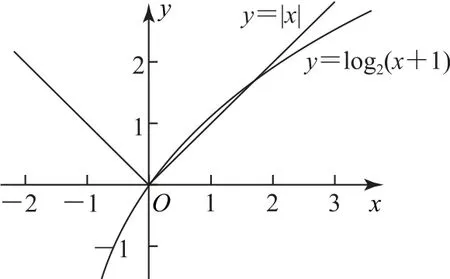
图3
(2)若0<a<1,由于x∈(1,2],logax<0,而(x-1)2≥0,故(x-1)2<logax无解.
若a>1,由于x∈(1,2],logax>0,而(x-1)2≥0,令f(x)=logax,g(x)=(x-1)2,画出两个函数的图像,如图4所示,要想(x-1)2<logax在x∈(1,2]内恒成立,则loga2>1,解得a∈(1,2),故选B.

图4
点评本题是不等式恒成立问题,解答的关键是将原问题转化为二次函数与对数函数图像的位置关系问题,进而通过函数图像让问题轻松获解.
3 比较数值大小
比大小问题是高考常考题型,这类问题不仅考查函数的单调性,同时考查考生灵活应用函数图像解决问题的能力.
例3已知函数f(x)=-2x,若2a=log2b=c,则( ).
A.f(b)<f(c)<f(a)
B.f(a)<f(b)<f(c)
C.f(a)<f(c)<f(b)
D.f(c)<f(b)<f(a)
解析f(x)=-2x在R 上单调递减,在同一平面直角坐标系中作出y=c,y=2x,y=log2x,y=x的图像,如图5 所示,则a<c<b,故f(b)<f(c)<f(a),故选A.

图5
点评由于指数函数与对数函数互为反函数,且它们的图像关于直线y=x对称,于是通过在同一平面直角坐标系中画出直线y=c,就可得出交点的横坐标,进而结合函数单调性比较大小.
4 求方程根的代数式值或范围
对于求与对数函数方程根的代数式值或范围这类问题,并不要求我们把方程的根全部求出来,而是要根据根的分布情况来求代数式的值或范围,因此这类问题可以采用数形结合的方法求解.

图6
点评本题通过作图发现方程的根与根之间的内在联系,即它们的分布具有对称性或互为倒数,这是解决此类问题的突破口,所以求解这类问题应关注方程各个根之间的联系.
以上例子说明对数函数图像的重要性,总而言之,若遇到用常规方法无法求解与对数函数有关的方程根问题、函数零点问题、取值范围问题、不等式问题等,则可以考虑利用数形结合方法求解.
(完)

