寻结构之表 育素养之里——以苏科版数学九（上）“二次函数”章首课教学设计为例

■杨丽华

《义务教育数学课程标准（2022 年版）》指出：“为实现核心素养导向的教学目标，不仅要整体把握教学内容之间的关联，还要把握教学内容主线与相应核心素养发展之间的关联。”教师要注重教学内容的结构化，重视单元整体教学设计，改变过去以课时为单位的教学设计，促进学生对数学教学内容的整体理解与把握。鉴于此，笔者以苏科版九（上）“二次函数”章首课为例，以促进学生数学抽象、数学建模等核心素养的培育和发展为目的，进行了单元整体教学的设计和实践。

一、学情分析

一次函数、反比例函数分别是八（上）第六章、八（下）第十二章的教学内容，通过一次函数、反比例函数的学习，学生积累了丰富的函数学习经验，具备了一定的函数学习的基本能力，对初中函数“变量说”“建模意识”有了一定的认知，为“二次函数”的学习奠定了基础。

二、教学目标

通过实际情境，直观地感知并抽象出量与量之间的函数关系，理解二次函数的概念及一般形式；通过类比已学函数的研究方法和经验，学习二次函数，整体建构本单元的知识脉络和研究方法。

三、教学过程

1.立足教材，重构情境

问题学校打算用16 米长的篱笆围成长方形的生物园饲养小兔，怎样围可使小兔的活动范围较大？

预设1请找出问题中蕴含的量以及量与量之间的关系。

设计意图：学生容易感知已知量、长与宽的和为8、面积等于长乘宽，但较难感知量与量之间的关系，尤其看不出面积与边长的函数关系，需要教师加以引导。本问题从学生熟悉的情境引入，贴合学生的心理需求，能激发学生的好奇心，让学生带着怀疑的眼光，重新审视教师的意图。结构不良型问题有利于拓展学生的思维宽度，结合教师的启发和引导，能帮助学生发现函数表达式，并通过设未知数来简化文字表述，从而帮助学生用数学的眼光来看待实际问题。

预设2请用列表的方式，列举出整数解的情况，并进行观察、发现。

学生通过观察、发现，得到初步结论：当一边长为4时，面积的最大值为16。但所列举的数据没有包含全部数据。教师追问，如果把“16米长的篱笆”改成“18米长的篱笆”，情况又会是什么样的呢？

设计意图：学生再次列表（如表1），发现表格中的最大数值20 不是正确答案，从而体会列举法的局限性。于是，教师引导学生寻找量与量之间的变化规律，带领学生回想哪个知识是刻画量与量之间关系的。学生容易想到是函数，通过设一边为x，面积为y，得到函数关系y=x（9-x）。由此，体现了学习二次函数的必要性，解决了“为什么学”的问题。

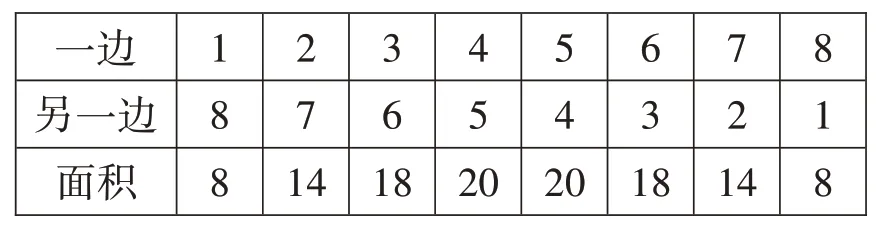
表1

2.异中求同，形成概念

在学生明确了“为什么学”的基础上，需要让学生明白“学什么”，也就是学习二次函数的概念。而概念教学离不开现实情境，通过不断抽象变量与变量之间的关系，将实际问题抽象成数学问题，并通过比较、类比加以解决。

预设3请写出以下实际问题中量与量之间的函数表达式。

（1）南京到上海全程约300km，一辆汽车从南京出发，匀速驶向上海。a.写出汽车全程所用时间t（h）与匀速行驶速度v（km/h）之间的函数表达式；b.若汽车匀速行驶的速度为100 km/h，写出汽车距离上海的路程S（km）与行驶的时间t（h）之间的函数表达式。

（2）水滴激起的波纹不断向外扩展，写出所形成的面积S与半径r之间的函数表达式。

（3）一面长与宽之比为2∶1 的矩形镜子，四边镶有边框，已知镜面的价格是每平方米120 元，边框的价格为每米30 元，加工费为45 元，写出总价y（元）与镜面宽x（m）之间的函数表达式。

（4）正方形包装盒的棱长为a（cm），写出正方体包装盒的体积v（cm3）与棱长a（cm）之间的函数表达式。

设计意图：借助等量关系，学生可以写出相应表达式。在此基础上，学生通过分类、辨析，找出哪些是熟悉的函数，哪些是陌生的函数。当学生将这些不同的函数进行分类后，心里自然有了一个标准，再类比一次函数的命名方式，得出二次函数的定义。

预设4（1）请判断下列函数是否为二次函数。如果是，写出其中的二次项系数、一次项系数和常数项：y=x2-x+1，y=3x-1，y=

（2）写出一个二次函数的表达式，让同桌判断其是否是二次函数，并指出哪些是二次项系数、一次项系数和常数项。

设计意图：再次辨析二次函数，加强对二次函数概念、各项系数的理解。学生通过自己出题，同伴解答，巩固对概念的掌握，明确二次函数定义的组成要素；体会引入二次函数的实际背景，探索实际问题中两个变量之间的数量关系，通过写函数表达式的过程，感受将实际问题数学化的基本方法。

3.类比提炼，形成框架

单元教学设计关键在于让学生形成知识框架，而知识框架的形成来源于同一类知识研究的路径与研究方法。对二次函数而言，它的前置知识是一次函数和反比例函数。学生对此有了一定经验，可以通过类比教学，形成知识框架。

预设5与一次函数一样，研究了二次函数的定义之后，我们还要研究二次函数的图像、性质以及应用。请利用表1 的数据，通过描点的方式，尝试画出函数图像。

设计意图：利用所画图像的性质，很好地解决了课前提出的问题。问题始终围绕一个情境展开，贯穿整个教学过程。知识主线将知识体系串成一线，方法主线使学生形成一般经验。

4.立足本质，寻根溯源

对于函数而言，列表、函数表达式、函数图像都能客观反映同一个函数，都刻画了量与量之间的对应关系。

预设6对于以下三种形式：列表（表格略）、表达式y=x（9-x）、图像（图像略），你能看出每种形式中变量的对应关系吗？

预设7寻找其中两种形式间的相互关系。

表格与函数表达式的相互关系，主要是待定系数法的相关应用；表格与图像之间的关系，主要是“点”与“形”的相互转化；函数表达式与函数图像是研究的重点，图像可以说明函数的性质特征，函数表达式的不同形式可表征图像的具体特点。

设计意图：二次函数作为初中阶段代数部分的最后一个环节，与数、式、方程、不等式之间都有关联，更加深刻地刻画了量与量之间的对应关系、数与形之间的内在关系，对学生的思维宽度和广度提出了更高的要求。根据三种函数的表示方式，提炼函数的本质特征，让学生逐步学会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界。

四、教学思考

1.结构化导图是建构知识整体性的有效手段

“建构”指建立和构造关于新知识认知结构的过程。“建立”一般指从无到有的兴建，“构造”则指对已有的材料、结构、框架加以调整、整合或者重新组合。主体对新知识的学习，同时包括建立和构造两个方面，既要建立对新知识的理解，将新知识与已有知识建立恰当的联系，又要将新知识与原有的认知结构相互结合，构造新的认知结构。

从知识结构上看，结构化导图能直观展示知识间的相互关联；从路径结构上看，结构化导图能客观地厘清知识的研究方法与研究路径，基于初中各阶段函数的学习，形成一般观念。教师有意识地进行结构化系列性渗透，在知识体系和数学体验中，更有利于学生拓展思维水平，提高数学核心能力，形成对客观世界认识的一般观念。

2.单元化教学是提升学生核心素养的有效途径

单元教学是对内容及其反映思想的进一步提炼和概括，是研究对象的方法论，以发展学生核心素养为目标，以“大概念”为引领，用全局的观点优化知识结构，鼓励学生充分表达与交流，帮助学生获得“四基”，发展“四能”，从而形成核心能力。

在实际单元教学中，首先要避免单元概念的泛化，避免将非主干的知识技能、解题技巧作为学习单元，避免过度总结解题模型，要有“破”模型的意识。《义务教育数学课程标准（2022 年版）》中提到的建模意识，是思考问题、解决未知世界的一种思维方式，但教师不应以解题模型固化思维，阻碍学生数学核心素养的形成。其次，单元教学除了知识的结构化、研究方法的结构化，更需要思维的结构化，因为思维的结构化才是单元教学的精髓。“单元”是落实素养目标的锚点，更是撬动课堂转型的支点，进而实现为素养而教。