初中数学大单元教学中信息技术应用研究

■陈浩宇

《义务教育数学课程标准（2022 年版）》指出：探索大单元教学，积极开展主题化、项目式学习等综合性教学活动，促进学生举一反三、融会贯通，加强知识间的内在关联，促进知识结构化。初中数学大单元教学是以单元为学习单位，以课程标准为依据，聚焦数学核心素养，围绕某一主题或活动（大概念、大任务、大问题），对教学内容进行整体思考、设计和组织实施的教学过程。

信息技术与初中数学课程相融合，对开展大单元教学有着促进作用。信息技术与大单元教学的融合不是简单地做“加法”，而是根据“教、学、评”的一致性进行有效融合，提升整体教学效率。教师利用多种数学教学工具对图形、数字、动画乃至声音、背景等教学内容进行综合处理，将抽象的数学知识直观化，帮助学生理解和掌握，并建构知识体系。学生在技术环境的浸润下，利用计算机等工具提取资料、交互反馈进行学习，降低了学习的难度，提高了探索能力，提升了学习效果。

一、将信息技术作为显示工具，以承上启下促进整体结构构建

在大单元教学中，数学教学内容需要以“大信息量”作为支撑，连接新旧知识，让学生整体把握知识结构，在整体、完整的结构中理解每一个数学知识。将信息技术与数学教学有效融合，可以充分发挥教师的主导作用，体现学生的主体地位，促进学生的深度思考，培养学生的核心素养。

例如，在教授“丰富的图形世界”时，教师提出问题：我们刚刚认识了很多几何图形，你能不能将它们进行分类呢？

学生先独立思考1 分钟，然后以4 个人为一组合作交流，最后由小组代表分享结论。

师：我们生活在一个丰富的图形世界中。请结合你的分类，尝试操作inRm3D 软件，并说一说图形的变化过程。

在教师的指导下，学生操作软件，感受“柱→台→锥”和“棱→圆”的变化过程，并通过交流形成结论。

师：大家一起来看动态视频，观察“点→线→面→棱柱→圆柱→圆台→棱台→棱锥→圆锥→线→点”的变化过程。

设计意图：本节课作为初中数学几何教学的第一节课，属于初中几何图形知识学习的起始阶段，是大单元教学中的“起始课”，对后续相关知识的学习影响深远。作为一节典型的“大单元课”，教师借助信息技术，在教学时应从学生“学会什么”出发，直观体会几何体之间的联系与区别，形成大视角，构建出几何图形的框架和演变过程。通过数学知识、方法与思想的整合设计，学生在完成任务中学会学习，深度思考“怎样学”，逐步弄清“能解决其他什么问题”等。

二、将信息技术作为探究工具，以进阶思路搭建学习过程

在设计完整的学习过程中，教师需要考虑到：学生需要什么样的基础知识和基本技能才能在大单元教学中达到预期的学习效果？教师需要安排哪些学习任务才能使学生具备所需的核心素养？结合预期的学习目标，学生需要哪些指导？教师应该如何更好地提供指导？提供什么材料和资源最有助于实现这些目标？而信息技术作为探究工具，以进阶思路搭建学习过程，从而促进学生学习目标的达成。

例如，在教授“展开与折叠”一课时，教师组织了如下学习任务：

任务一 展开

师：将一个正方体的表面沿某些棱剪开，能展开成一个平面图形吗？

学生动手操作。教师利用希沃直播软件，投屏展示学生操作过程，再用GeoGebra软件演示正方体的动态展开过程。

师：你还能得到哪些平面图形？与同伴进行交流。

教师用Shapes-3D 软件演示展开过程，并归纳出不同的展开图，丰富学生认知，发展学生的空间观念。

任务二 折叠

师：请你把刚展开的正方体平面图再恢复成正方体，并标出相对面的小正方形，可以把相对面用相同字母或颜色来标注。你能在展开图上找到每个面折好后的相对面吗？

教师用Shapes-3D 软件演示折叠过程，让学生体会展开与折叠之间的联系与区别。此外借助信息技术工具，利用希沃白板软件采集学生的答题信息，及时进行投屏展示，提高课堂教学的效率，体现技术的应用价值。

设计意图：借助任务一，学生经历模型展开等活动，将一个正方体的表面沿某些棱剪开，展开成一个平面图形，并归纳形成一般化认识；任务二通过折叠的实践操作（模型与技术），进一步认识立体图形与平面图形的关系。学生在展开图上找到相对面，在此过程中，信息技术的使用有助于学生顺利实现由感性认识到理性认识的过渡，从而有效地降低难度，分散难点，突破思维障碍，初步建立空间观念，发展几何直观，积累数学活动经验。

三、将信息技术作为反馈工具，以全程一致创设评价任务

在大单元教学实践中落实“教、学、评”的一致性，既可以实现教学目标的要求，又可以衡量学习与目标的差距，检测目标的实现情况，并通过反馈及时改进学习。因此，将信息技术作为反馈工具，将评价任务嵌入学习的全过程，并统一、持续地指向学习目标，不仅有利于破除知识点和课时的碎片化教学设计，还能够促使教学活动形成动态互动的联结，在单元内部建立“大观念”。

例如，在学习“勾股定理”时，学生经历了“发现规律→猜想命题→严格证明→得出定理→实际运用”的过程，充分体会数形结合和从特殊到一般的思想方法。最后，教师设计以下的评价任务。

1.如图1，求图中字母所代表的正方形的面积。

2.在△ABC中，∠C=90°，AB=c，BC=a，AC=b。

（1）a=6，b=8，求c；

（2）a=8，c=17，求b。

3.历史上的各种证明方法有五百多种，利用网络查询不同的证明方法，并整理四种。

4.（1）如图2，以Rt△ABC的三边为直径的3个半圆的面积之间有什么关系？

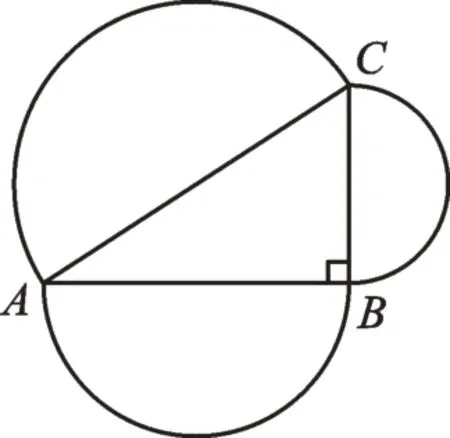
图2

（2）若Rt△ABC为一般三角形，那么刚才的结论还成立吗？

设计意图：第1 题和第2 题是勾股定理的基本计算，关键是已知直角三角形的两边长能求第三条边的长度，属于基础练习，可在课堂上或者课后作为必做题完成；同时，学生进行在线答题，即时生成答题信息，形成有效反馈。第3题主要是让学生自主了解关于勾股定理的文化历史背景。利用互联网资源的优势，以不同的资源丰富学生认识，培养学生的民族自豪感，让学生深刻了解数学史，感受数学之美。不同学生根据自己的学习水平与能力选择性地完成第4题，继续挖掘勾股定理的不同视角的应用，构建思维框架，让因材施教的素质教育理念落到实处。

此外，教师适当布置线上作业，不仅可以激发学生学习兴趣，也可以针对学生的作业内容进行在线修改，从而更及时、全面地掌握学生的学习情况，做出及时评价。学生也可以在线请教教师解决疑难问题，消除时空障碍，提升学习效率。