平行多幅连续钢箱梁桥抗风性能研究

郭文超, 夏 伟, 黄智文, 罗 祎, 华旭刚, 温 青

(1. 湖南大学 风工程与桥梁工程省重点实验室,长沙 410082; 2. 安徽省交通勘察设计院有限公司,合肥 230011; 3. 中铁大桥勘测设计院集团有限公司,武汉 430101; 4. 湖南科技大学 土木工程学院,湖南 湘潭 411201)

连续钢箱梁桥具有自质量轻、截面抗弯和抗扭刚度大、施工周期短、抗震性能好等特点,是大跨度连续梁桥的有力竞争桥型之一,近年来在我国发展迅速[1]。例如,我国的崇启大桥[2]、港珠澳大桥深水区非通航孔桥[3]、黄茅海跨海通道引桥[4]、深中通道泄洪区非通航孔桥[5]等采用连续钢箱梁的结构形式。然而,大跨度连续钢箱梁桥自振频率低、固有阻尼小、且多为典型的钝体断面, 因此极易发生中、低风速下的竖弯涡振,并对桥面行车安全和大桥的正常运营造成不利影响。例如,巴西的里约罗尼泰大桥(主跨300 m)经常在14～22 m/s的风速下发生大幅竖向涡振,为了避免危及行车安全,不得不在涡振锁定风速区间关闭桥梁,并最终采用调谐质量阻尼器(tuner mass damper,TMD)进行涡振控制[6]。日本的东京湾航道桥(主跨2 m×240 m)通过节段模型风洞试验、气弹模型风洞试验和现场实测都观测到主梁容易在14 m/s以上的风速下发生大幅竖向涡振,最终采用气动措施和TMD进行联合涡振控制[7]。我国崇启大桥(主跨4 m×185 m)通过风洞试验发现主梁在15～27 m/s的风速下容易发生一阶竖弯模态的竖弯涡振,并最终采用TMD进行涡振控制[8]。俄罗斯伏尔加河大桥(主跨7 m×155 m)在实测风速11.6～16.6 m/s发生了大幅竖向涡振,最终采用了半主动TMD进行振动控制[9]。

大跨度连续钢箱梁桥通常采用单幅或双幅布置形式,例如日本东京湾航道桥和巴西约罗尼泰大桥为单幅布置形式,而崇启大桥则为双幅布置形式。当采用双幅布置时,由于上、下游桥梁之间的气动干扰效应,大桥发生涡振和驰振的风险一般都会显著提高。秦浩等[10]以崇启大桥为背景通过气动模型风洞试验研究了双幅连续钢箱梁桥的涡振特性,发现分离式双幅桥存在两个竖向涡振区间,分别以上游桥和下游桥的涡振为诱导因素,且下游桥的涡振响应更大。杨群等[11]采用节段模型风洞试验研究了主梁间距对并列双幅钝体箱梁涡振振幅及风速锁定区间的影响,发现当相邻主梁净间距与主梁宽度之比在0.2～4.0时,下游箱梁的涡激共振有显著的被放大效应。董国朝等[12]以一座主跨178 m三跨连续钢箱梁桥的跨中截面为研究对象,结合节段模型风洞试验和计算流体力学(computational fluid dynamics,CFD)数值仿真分析研究了并列双幅钝体钢箱梁的气动干扰效应,发现上游桥下表面的周期性漩涡脱离是双幅桥涡振的关键诱因。由于城市桥位资源紧缺,并列双幅桥不仅应用于大跨度连续梁桥,在斜拉桥和悬索桥等其他桥型中也常有应用。陈政清等[13]以佛山平胜大桥为背景,研究了双幅桥的气动干扰效应对钢箱梁悬索桥涡振性能的影响,结果发现当双幅桥的间距较小时,气动干扰效应可能对两幅桥的涡振性能产生不利影响。朱乐东等[14]以天津塘沽海河斜拉桥为例,分析了气动干扰效应对箱型平行分离双幅桥颤振和涡振性能的影响,结果表明气动干扰效应对下游桥梁的涡振和颤振性能影响比上游桥更大。刘志文等[15]研究了主梁间距对串列双幅流线型钢箱梁颤振性能的影响,结果表明在一定的间距比范围内,间距越小双幅桥颤振临界风速的降低程度越严重,而且软颤振发生的可能性也越大。刘小兵等[16]开展了中等间距双钝体箱梁的气动干扰效应试验,结果发现负攻角下气动干扰效应主要放大下游桥梁的涡振相应,正攻角下气动干扰效应对上游桥梁的涡振有显著干扰效应。谭彪等[17]研究了间距比对叠合梁双幅桥涡振性能的影响,结果发现双幅桥的最不利间距比为2～4。陈平等[18]以甬江铁路桥为背景,研究了平行三幅桥之间的气动干扰效应,结果表明气动干扰效应会显著降低下游桥的颤振临界风速。Kim等[19]在韩国珍岛大桥上观测到了双幅并列斜拉桥的竖向涡振,并通过节段模型风洞试验进一步研究了主梁间距和上游桥桥梁的频率差异对双幅桥涡振性能的影响。

综上所述,大跨度连续钢箱梁桥在常遇风速下容易发生竖向涡振,并列双幅或多幅桥则可能进一步加剧桥梁发生大幅竖向涡振,甚至驰振的风险。目前并列桥梁抗风性能研究多以双幅流线型钢箱梁的涡振和颤振为对象,有关两幅以上并列钝体钢箱梁涡振和驰振性能的研究非常稀少。实际上,大跨度连续钢箱梁桥一般采用变截面,其气动力特性具有显著的三维效应,远比等直截面的流线型钢箱梁复杂。本文以一座在建的平行四幅连续钢箱梁桥梁为背景,通过单幅和多幅桥的节段模型风洞试验,以及单幅和多幅桥的气弹模型风洞试验,对其涡振和驰振性能进行了深入研究。

1 工程背景

引江济淮工程G312 合六叶公路桥位于江淮沟通段 K42+271 m 处,跨越江淮沟通段航道。大桥由四幅跨径布置均为(100+180+100)m 的变高度直腹板连续钢箱梁组成。全桥桥面全宽52.5 m,四幅钢箱梁均采用单箱单室结构,其中位于两侧的第一幅和第四幅桥,以及位于中间的第二和第三幅桥分别关于道路中心线对称(如图1所示)。第一、第四幅钢箱梁顶板宽度为 11.75 m,底板宽 6.25 m;第二、第三幅钢箱梁顶板宽度为 13.25 m,底板宽 6.25 m。第一、第二幅桥和第三、幅桥之间的净间距均为0.75 m,第二、第三幅桥之间的净间距为1 m。四幅桥左右两侧的防撞栏杆或人行道栏杆上均设置有采用细钢丝编织而成的防抛网,第一和第四幅桥的右侧还设置了人行栅栏以区分自行车道和人行道,检修车轨道设置在直腹板中部以上。在立面上,大桥中支点处梁高为9 m,中跨跨中直线段和边跨端部直线段梁高为 4.5m,变高段底面线形为圆曲线,钢箱梁顶板设置单向 2%的横坡,底板水平。桥梁平面线形设计服从道路平面线形设计,由于道路中心线与航道中心线成一定夹角,所以各幅桥之间桥墩沿河道斜向错位布置,但桥墩轴线与桥梁中心线保持垂直正交,图2和图3给出了大桥的平面和立面布置图。

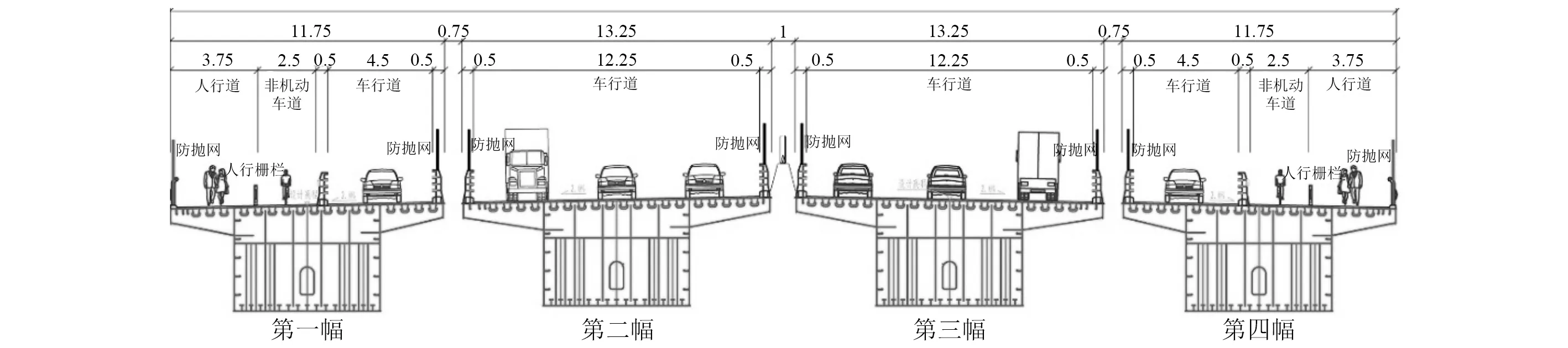
图1 桥梁横断面布置图(m)Fig.1 Cross-section of heliuye highway bridge(m)

图2 大桥平面布置图Fig.2 Floor plan of heliuye highway bridge

2 节段模型风洞试验研究

2.1 单幅桥的风致振动响应

根据我国JTG/T D60-01—2018《公路桥梁抗风设计规范》,对于大跨度连续钢箱梁桥应重点检验其涡振和驰振性能。本桥采用变截面钢箱梁,箱梁高度从中跨支点处的9 m逐渐过渡到中跨跨中的4.5 m。参考东京湾航道桥的抗风设计研究,首先选取第一、第二幅桥中跨跨中截面和第一幅桥中跨L/6截面,一共制作三个几何缩尺比为λL=1∶40的单幅桥梁节段模型,以研究大桥的涡振和驰振性能。选择中跨跨中截面作为研究对象,是因为低阶模态下跨中截面处的位移最大;选择中跨L/6截面作为研究对象是因为该截面实桥高度为6.54 m,约为中跨L/2截面与支点截面高度之和的一半,其气动外形具有代表性。表1～表3分别给出了第一、第二幅桥中跨跨中截面和第一幅桥中跨L/6截面的节段模型关键设计参数。第二幅桥中跨截面与第一幅桥中跨截面的关键区别在其桥面宽度为13.25 m,其竖弯基频为0.729 Hz,其余设计参数与第一幅基本相同。第一幅桥L/6截面与第一幅桥中跨截面的关键区别在于其实桥梁高为6.54 m,其他设计参数与第一幅桥基本相同。图4给出了节段模型在风洞中的试验照片。

表1 第一幅桥跨中截面节段模型设计参数Tab.1 Design parameters of segmental model of the first span mid-section

表2 第二幅桥跨中截面节段模型设计参数Tab.1 Design parameters of segmental model of the second span mid-section

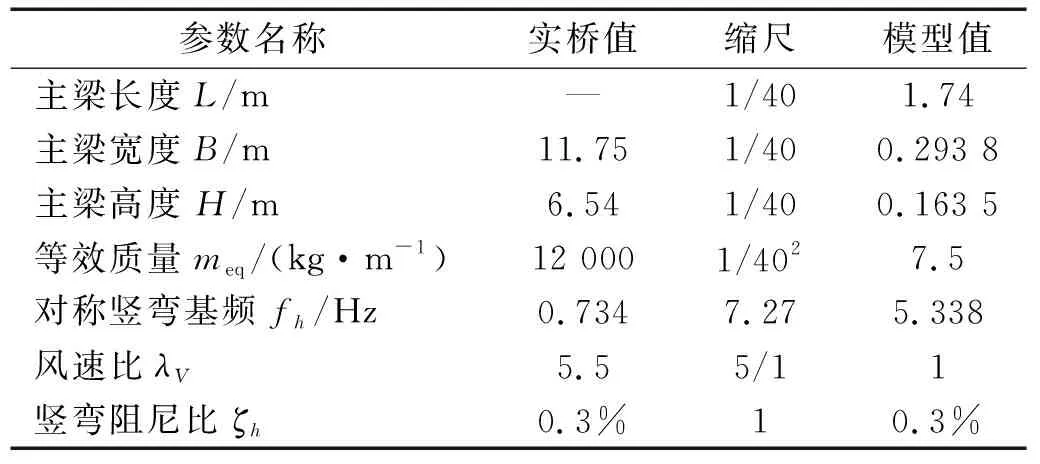
表3 第一幅桥中跨L/6截面节段模型设计参数Tab.3 Design parameters of segmental model of the L/6 section of the first bridge

图4 单幅桥节段模型风洞试验照片Fig.4 Wind tunnel test of sectional model of the single bridge

选取0°,-3°,3°等三个风攻角开展节段模型风洞试验,因为第一幅桥包含有人行道栅栏,其左右截面不对称,所以其跨中截面节段模型风洞试验探究了人行道和防撞栏杆分别迎风时的风致振动响应,对应的L/6截面则仅探究了防撞栏杆迎风时的风振响应,第二幅桥为对称截面,来流风向不影响试验结果。

对比图5和图6可以发现,对于非对称断面,迎风侧不同,断面的气动性能也完全不同。对于第一幅中跨跨中截面,当人行道迎风时,主梁在-3°风攻角下会发生竖向涡振响应,且存在两个竖向涡振响应区间,其中第一个竖向涡振区间发生在风速20 m/s左右,此时的最大位移均方差值只有2.5 mm,远小于抗风规范容许的涡振限值38 mm;第二个涡振区间发生在35～42 m/s的风速区间,最大位移均方差为17.6 mm,是规范容许值的46.3%。大桥在0°和3°风攻角下均会发生驰振响应,驰振临界风速是节段模型竖弯振动下,振幅突然增大点对应的风速,由图5可知大桥在0°和3°风攻角下对应的驰振临界风速分别为55 m/s和44 m/s,均大于驰振检验风速39.4 m/s。当防撞栏杆侧迎风时断面的气动性能明显恶化,其中-3°风攻角下主梁发生了大幅竖向涡振,其涡振风速锁定区间与人行道迎风时保持不变,但最大涡振位移均方差达到了177.6 mm,是规范容许值的4.7倍;主梁在-3°和3°风攻角下仍然会发生驰振响应,而且驰振临界风速相对人行道迎风明显降低,两种工况下的驰振临界风速均约为42 m/s。

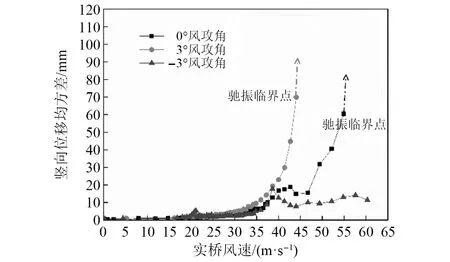
图5 第一幅桥中跨跨中截面主梁竖向位移响应随风速变化曲线(人行道迎风)Fig.5 Variation of amplitude of VIV of main girder with wind speed in the mid-span section of the first bridge(Sidewalk guardrail against the wind)

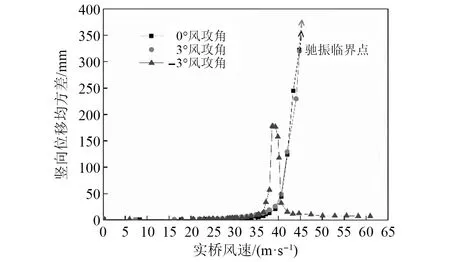
图6 第一幅桥中跨跨中截面主梁竖向位移响应随风速变化曲线(防撞栏杆迎风)Fig.6 Variation of amplitude of VIV of main girder with wind speed in the mid-span section of the first bridge(Crash barriers against the wind)

对比图7和图6可以发现,第二幅桥的抗风性能与第一幅桥也存在显著差异,说明断面的宽高比对其抗风性能有显著影响。第二幅桥中跨跨中截面在0°和-3°风攻角下均会发生竖向涡振响应,其中-3°风攻角下的涡振风速锁定区间为35～42 m/s,与第一幅桥基本相同,但最大涡振位移均方差为74.8 mm,要远小于第一幅桥。第二幅桥在3°风攻角下也会发生驰振响应,其临界风速约为49 m/s。

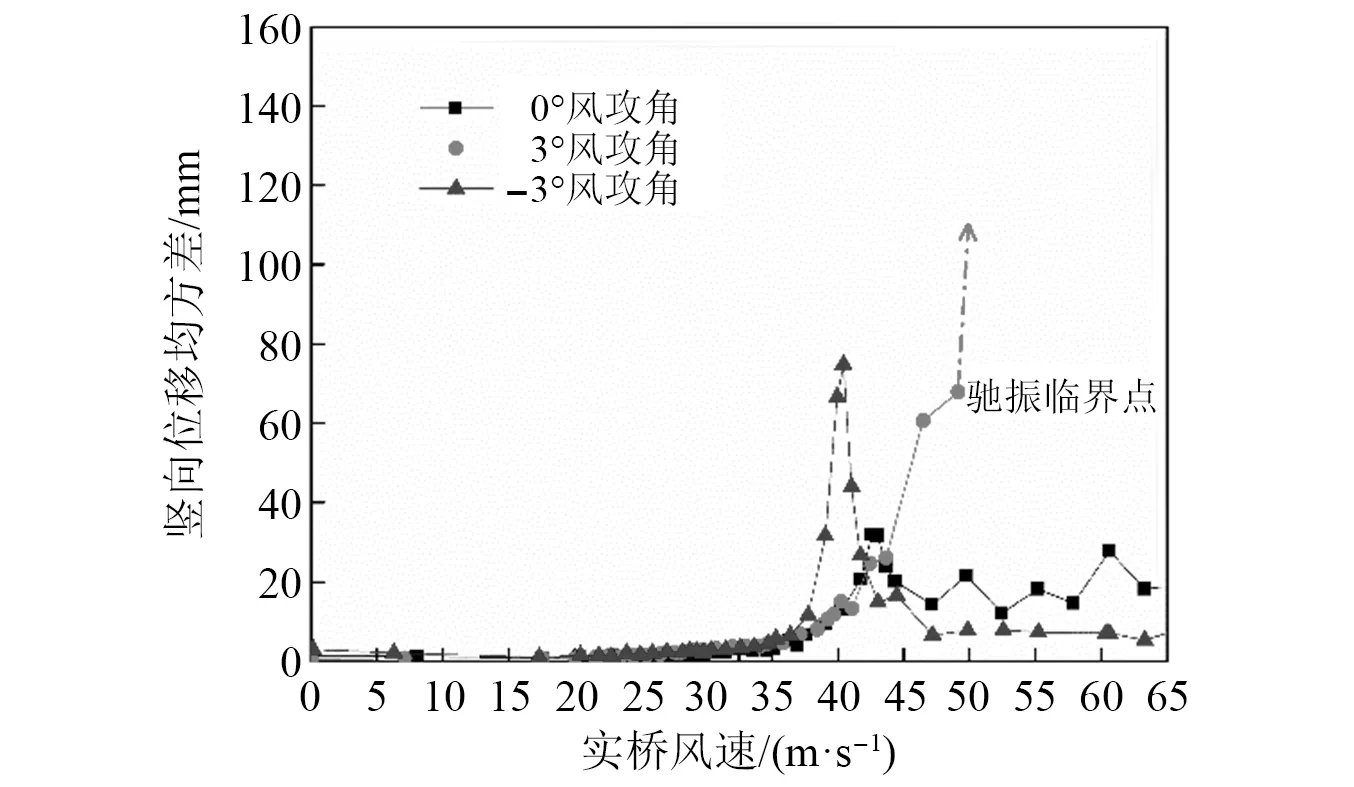
图7 第二幅桥中跨跨中截面主梁竖向位移响应随风速变化曲线Fig.7 Variation of amplitude of VIV of main girder with wind speed in the mid-span section of the second bridge

图8为第一幅桥L/6截面的竖向位移响应随风速的变化曲线。对比图8和图6可以发现,随着断面高度的增大,主梁在0°和3°风攻角下的驰振性能基本保持不变,驰振临界风速与中跨跨中截面基本相同。但主梁高度增加后在-3°风攻角下不再发生涡振响应,而是发生了驰振响应,相应的驰振临界风速约为45 m/s。

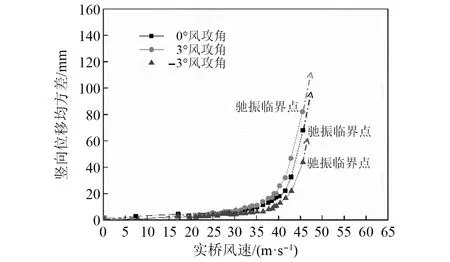
图8 第一幅桥中跨L/6截面主梁竖向位移响应随风速变化曲线(防撞栏杆迎风)Fig.8 Variation of amplitude of VIV of main girder with wind speed in the L/6 section of the first bridge(Crash barriers against the wind)

综上所述,对于单幅桥梁,主梁梁宽的变化、主梁梁高的变化以及断面气动外形的不对称性都会对主梁的气动性能产生显著影响。总体来看,在梁高不变的情况下,梁宽的增大对于改善主梁的涡振和驰振影响是有利的;在梁宽不变的情况下,增大梁高对主梁的驰振性能是不利的,但对主梁的涡振性能是有利的。此外,因为实桥第一和第四幅桥对称布置,因此总是人行道一侧迎风,这样对降低主梁的涡振响应相应是有利的,对驰振性能的影响较小。

2.2 并列双幅桥和并列三幅桥的风致振动响应

选取第一幅桥和第二幅桥的中跨跨中截面,研究了3°风攻角下并列布置双幅桥的抗风性能,其中第一幅位于迎风侧,且以人行道一侧迎风。图9(a)给出了并列双幅桥的风洞试验照片,图9(b)给出了两幅桥的竖向位移均方差随风速的变化曲线。可以看到,并列双幅桥在3°风攻角下并没有像单幅桥一样发生驰振,而是在30～55 m/s的风速区间发生大幅竖向涡振,该风速区间的大小与单幅桥涡振情况相比范围扩大了一倍左右。从涡振振幅来看,位于下游的第二幅桥的涡振响应始终大于迎风侧的第一幅桥。例如,当风速为39.8 m/s时,上游桥和下游桥的涡振位移均方差分别为108.1 mm和455.4 mm,后者时前者的4.2倍;当风速为47.9 m/s时,上游桥和下游桥的涡振位移均方差分别为194.1 mm和555.2 mm,后者是前者的2.86倍。从涡振振幅随风速的发展趋势来看,上游桥和下游桥并不同步,其中下游桥在风速为47.9 m/s时先达到涡振响应峰值,而上游桥在风速为50.0 m/s达到涡振响应峰值。

图9 并列双幅桥节段模型试验(3°风攻角)Fig.9 Test of sectional model of the twin parallel decks(3° wind attack angle)

选取第一幅、第二幅和第三幅桥,研究了3°风攻角下并列布置三幅桥的抗风性能,其中第一幅桥位于迎风侧,第二和第三幅桥位于下游。图10(a)给出了并列三幅桥的风洞试验照片,图10(b)给出了三幅桥的竖向位移均方差随风速的变化曲线。可以看到,并列布置的三幅桥在3°风攻角下竖向位移从风速50 m/s开始不断增大,当风速达到60.5 m/s时三幅桥的振幅依然呈不断上升趋势,由此判断三幅桥均发生了软驰振响应。需要说明的是,由于三幅桥的竖向振幅均很大,而且试验风速较高,为了避免发生意外,并没有尝试更高的风速,因此更高风速下的振动响应还有待进一步验证。

图10 并列三幅桥节段模型试验(3°风攻角)Fig.10 Test of sectional model of the triple parallel decks(3° wind attack angle)

2.3 并列四幅桥的风致振动响应

实桥为并列四幅桥,因此节段模型风洞试验选取第一～第四幅桥的中跨跨中截面,研究并列四幅桥在-3°,0°和3°等三个风攻角下的风致振动响应。图11(a)给出了并列四幅桥在风洞中的试验照片,图11(b)～图11(d)分别为0°风攻角、-3°风攻角和3°风攻角下四幅桥的竖向位移均方差随风速的变化曲线。可以看到,在0～60 m/s的风速范围内,不同风攻角下四幅桥均没有发生大幅竖向涡振,也没有发生驰振现象。与单幅桥相比,位于下游的第三幅桥和第四幅桥由于上游桥梁引起特征紊流作用,会发生较大的抖振响应,而且抖振响应的幅值随着风速的增大而增大。从气动稳定性来看,并列四幅桥的涡振和驰振稳定性都要优于并列双幅桥和并列三幅桥,也说明了并列多幅桥的气动稳定性不仅与单幅桥气动性能相关,与相邻桥之间的间距相关,与桥幅数量也是紧密相关的。

图11 并列四幅桥节段模型试验结果Fig.11 Results of sectional model of the four parallel decks

3 气弹模型风洞试验研究

节段模型风洞试验能够准确反映等直截面并列多幅桥的风致振动特性,但对于本文涉及的变截面梁桥,为了更准确地反映由变截面引起的气动力三维特性对实桥气动稳定性的影响,需要开展气弹模型风洞试验。鉴于此,针对并列四幅桥的成桥运营状态,制作了第一～第四幅桥的全桥气弹模型。气弹模型的几何缩尺比λL=1∶55,频率比λf=7.84∶1,对于的风速比为λf=1∶7。由大桥平面布置图(见图2)可知,第一～第四幅桥为平行错孔布置,相应的气弹模型试验照片如图12(a)所示。考虑到大桥的驰振检验风速为39.4 m/s,以及HD-3风洞的最大风速试验能力,气弹模型试验的最大试验风速为43 m/s。

图12 平行错孔布置四幅桥气弹模型风洞试验结果Fig.12 Results of full-bridge aeroelastic model of the four bridges arranged in parallel staggered rows

图12(b)～图12(d)给出了气弹模型风洞试验结果。可以看到,在试验风速范围内,不同风攻角下,四幅桥都没有发生大幅涡振和明显的驰振发散现象。随着风速的增大,四幅桥的竖向位移都有逐渐增大的趋势,其中0°风攻角下四幅桥的竖向振动最小,3°风攻角下四幅桥的竖向振幅随风速增大最快。在3°风攻角下,随着风速地增大,从竖向振幅来看,始终有第四幅桥>第三幅桥>第二副桥>第一幅桥。对比图12和图11可以发现,由节段模型风洞试验得到的中跨跨中位移预测结果与气弹模型风洞试验基本一致,说明按并行错孔布置的四幅桥具有良好的气动性能,在检验风速范围内不易发生涡振和驰振现象。需要说明的是,如果改变平行四幅桥之间的间距,大桥的气动稳定性可能发生显著改变,因此对于间距的影响后续还将深入研究。

4 机理探讨

从图5～图11可知,单幅桥节段模型会出现涡振和驰振,并列双幅桥节段模型会出现涡振,并列三幅桥节段模型会出现驰振,但是并列四幅桥节段模型并不会出现明显的风致振动。该节通过CFD技术分析断面周边瞬时涡量演变,解释不同桥幅数量对桥梁气动性能的影响。本节仅以并列双幅桥和并列四幅桥节段模型为例,分析折算风速Vred=10(双幅桥最大涡振振幅对应的风速)下的涡量演变规律。

4.1 计算模型及网格划分

并列双幅桥试验方案和并列四幅桥试验方案CFD计算简图如图13所示,其中计算模型考虑了人行道栏杆、防撞栏杆、栅栏等,主梁断面CFD计算几何缩尺比取λL=1/40。

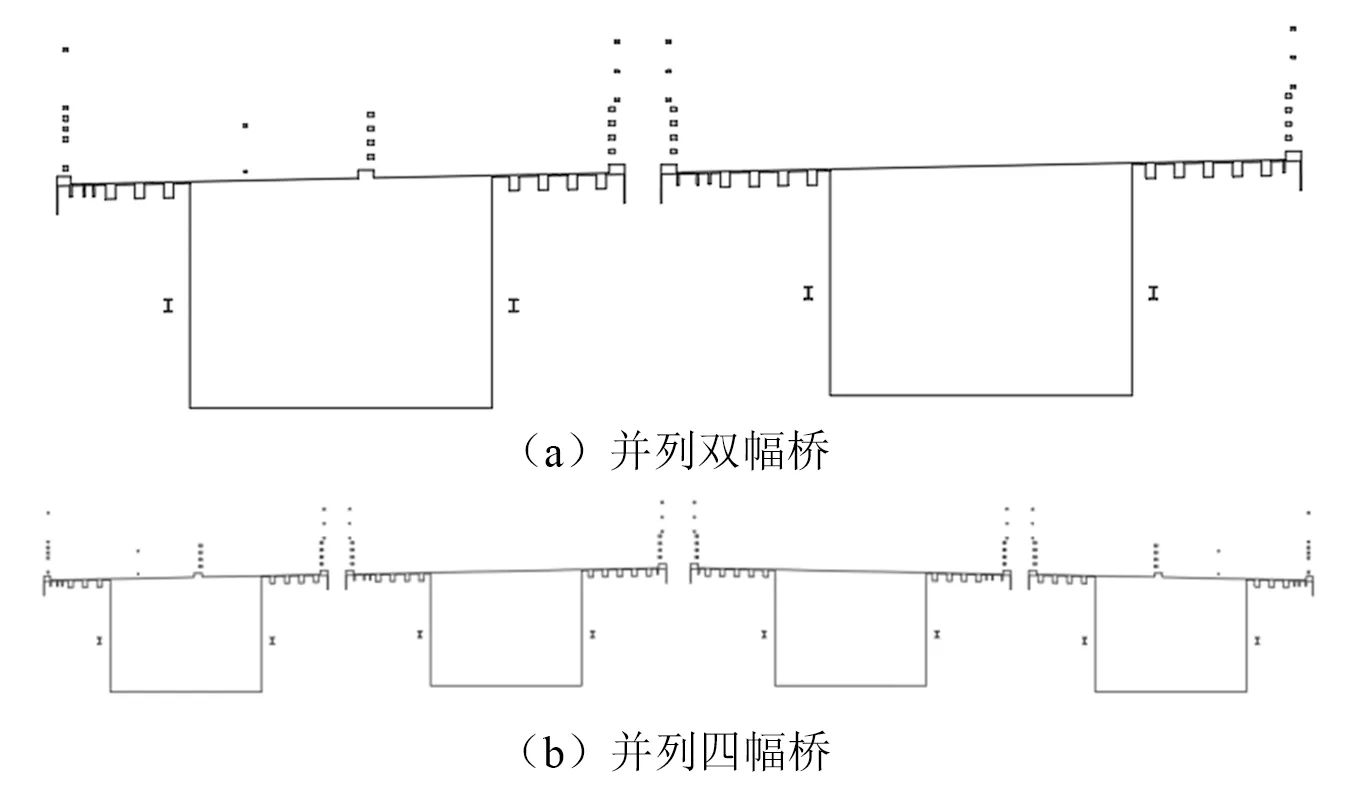
图13 CFD计算简图Fig.13 Simplified CFD model

主梁断面计算域确定如下:对于并列双幅桥数值模拟,计算域长为30B、宽为20B的矩形区域,双幅桥模型中心距计算域左侧边界及上下侧边界均为10B,距离右侧边界为20B;对于并列四幅桥数值模拟,计算域长为40B、宽为20B的矩形区域,双幅桥模型中心距离计算域左侧边界及上下侧边界均为10B,距离右侧边界为30B;其中B为第二幅桥的主梁宽度,双幅桥模型阻塞率约为0.06%,四幅桥模型阻塞率约为0.08%,均小于要求的5%。

计算域边界条件:计算域左侧边界设置为速度入口边界,计算域右侧边界设为压力出口边界,计算域上、下边界均设为对称边界,主梁断面(含附属措施)设置为无滑移避免边界。图14所示为并列双幅桥和并列四幅桥数值模拟计算域及边界条件设置,图15所示为并列双幅桥和并列四幅桥CFD模型网格划分图。

图14 计算域示意图Fig.14 Computational domain

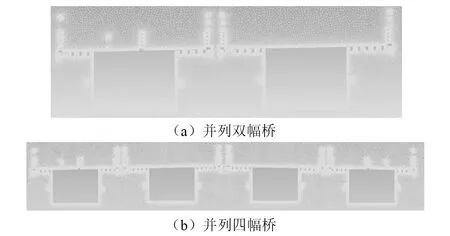
图15 CFD模型整体网格划分Fig.15 Global meshing of CFD model

4.2 试验结果机理分析

图16、图17所示分别为3°风攻角下,并列双幅桥节段模型和并列四幅桥节段模型在一个周期瞬时时刻值(0,T/4,2/T,3T/4)的瞬时涡量图。

图16 并列双幅桥静态绕流瞬时涡量图Fig.16 Instantaneous vorticity of flow around sectional model of the twin parallel decks

图17 并列四幅桥静态绕流瞬时涡量图Fig.17 Instantaneous vorticity of flow around sectional model of the four parallel decks

由图16可以发现,对于并列双幅桥,在尾流区域出现交替脱落的“卡门涡街”,结合试验结果,可以推断在尾流区域发生的周期性的漩涡脱落是诱发双幅桥涡振的主要。

由图17可以发现,并列四幅桥节段模型在一个周期内不同时刻的瞬时涡量图基本一致,与并列双幅桥类似,来流受到桥面板前缘的影响分别向断面上、下侧分离,但是在尾流区域没有产生周期性的漩涡脱落,所以未产生明显风致振动,与前文并列四幅桥3°风攻角下的试验结果一致。

5 结 论

(1)并列多幅桥的气动稳定性受单幅桥气动性能、风攻角和桥幅数量等众多因素的影响。对于相同的风攻角,随着桥幅数量的变化多幅桥的气动性能可在涡振、驰振和抖振等多个状态变化。

(2)与单幅桥、双幅桥以及三幅桥相比,按小间距平行错孔布置的四幅桥具有相对较稳定的气动性能,在试验风速范围内没有发生大幅涡振和驰振发散现象,但由特征紊流引起的抖振较为明显。

(3)对于并列多幅桥的竖向风致振动响应,一般下游桥大于上游桥。