物探节点布收车越障稳定性分析与底盘结构优化研究
黄志强, 孙浩翔, 雷雨薇, 王 凯
(西南石油大学 机电工程学院,成都 610500)
物探节点布收车是石油勘探领域的新型装备,搭载了用于布设与回收的智能机械手、放置地震节点的料库等,有效提升勘探效率,未来将会成为物探施工中代替人工作业的关键装备。车辆采用履带底盘,决定着在复杂环境行驶作业过程中的稳定性与安全性,然而,野外物探区域通常处于山地丘陵、沼泽、沙漠等复杂恶劣地区,其中山地障碍对车辆安全影响最大,越障时,履带前端在攀爬上障碍后,在重心的作用下车头将会继续仰起,直至重心越过障碍物,车辆落回地面,整个过程车辆剧烈振动,底盘机架承受巨大冲击力,有变形、产生裂纹甚至断裂的风险,并且由于车辆整车质量大、箱体高,导致重心位置更后、更高,越障时将承受更大的冲击载荷。因此,将平顺性和冲击作为稳定性评价指标,对车辆越障过程中的振动加速度标准差和峰值进行计算,分析底盘机架受力情况,找到应力集中位置,并对履带底盘进行结构优化,使车辆越障时所受振动、冲击更小,提高安全稳定性。
目前,履带车辆稳定性研究主要集中在车辆的控制方面,对车辆整体稳定性能研究较少,其中,准确建立履带车的动力学模型和正确的振动响应方法是研究整车稳定性的重要手段[1-4]。在履带车辆的稳定性方面,国内外学者根据不同类型的履带车做出了振动与冲击特性分析,如乔新勇等[5]在研究履带车辆的振动响应时考虑了履带环对其造成的影响,分析了在典型起伏路面下影响车辆振动的相关因素,但缺少极端越障路况;王军等[6]研究了履带式推土机在越障时所产生的冲击载荷对橡胶减振器的冲击响应特性,表明履带机架经减振后所受冲击减小。在履带行走装置的结构方面,Mezyk等[7]对履带行走装置在崎岖地形行驶时的悬架系统进行了分析,表明不同的张紧力会对车辆的稳定性造成影响,通过试验确定了合适的张紧力参数; Banerjee等[8]对履带战车建立了相应数学模型,通过仿真分析的方法模拟了车辆在不同环境下的稳定性能,验证了模型的高效、准确性。在履带车的优化方面,扈凯等[9]以优化车辆振动参数、改善稳定性为目标,基于模态规划法对履带拖拉机的底盘机架进行优化分析;庞荫铭等[10]对履带行走装置在常规路况下的机架进行了拓扑优化;毛智琳等[11]在满足整机稳定性和通过性的基础上对履带车辆的机架进行了优化,增强了机架强度。从上述研究可知关于履带稳定性方面的研究多数以复杂路面下的振动、冲击响应为研究内容,在履带底盘的优化过程中,大多数学者只对底盘机架进行了相关优化,却没有考虑到行走装置结构参数对越障稳定性能的影响,导致优化后的履带车辆虽然满足了强度需求,但是没从根本上提升越障稳定性。
针对上述问题,本文开展了物探节点布收车在越障工况下的动力学响应分析、机架瞬态响应分析以及结构优化研究。通过力学分析找出影响车辆越障时稳定性的关键因素,基于底盘机架应力分布情况发现车辆存在的问题,最后建立履带底盘行走装置结构参数与车辆的振动加速度标准差、垂向振动加速度峰值二阶响应模型,通过不同权重因子配比方式使两个优化目标满足设计需要,避免底盘损坏,为物探节点布收车底盘设计提供了参考,对石油勘探领域高效、安全、精准勘探具有重要意义。
1 履带底盘动力学建模分析
1.1 履带底盘模型的简化与建立
物探节点布收车的履带底盘包含机架和行走装置两部分,底盘搭载液压系统、发动机等设备,在多体动力学软件中会影响计算速度,增大计算量,故需要对其进行简化。建立了履带底盘的拓扑结构如图1所示,各轮系之间的约束关系如表1所示,简化后的动力学模型如图2所示。
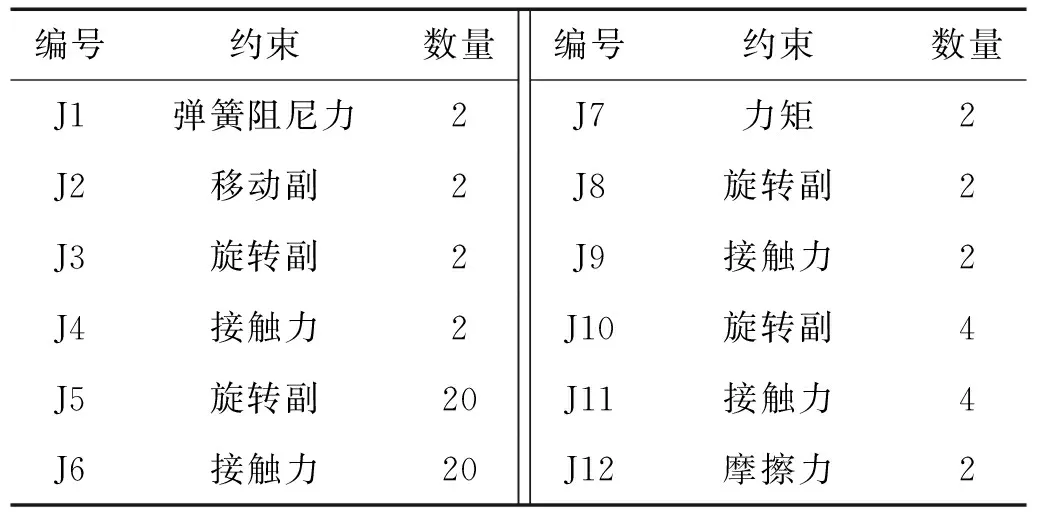
表1 履带底盘轮系约束关系Tab.1 Constraints between components of tracked chassis
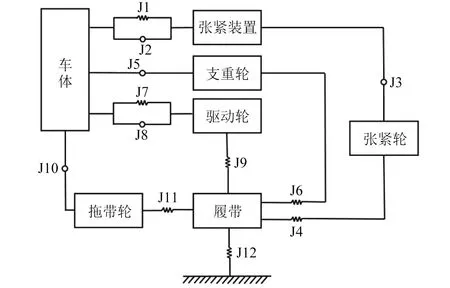
图1 履带底盘拓扑结构示意图Fig.1 Topology structure of tracked chassis
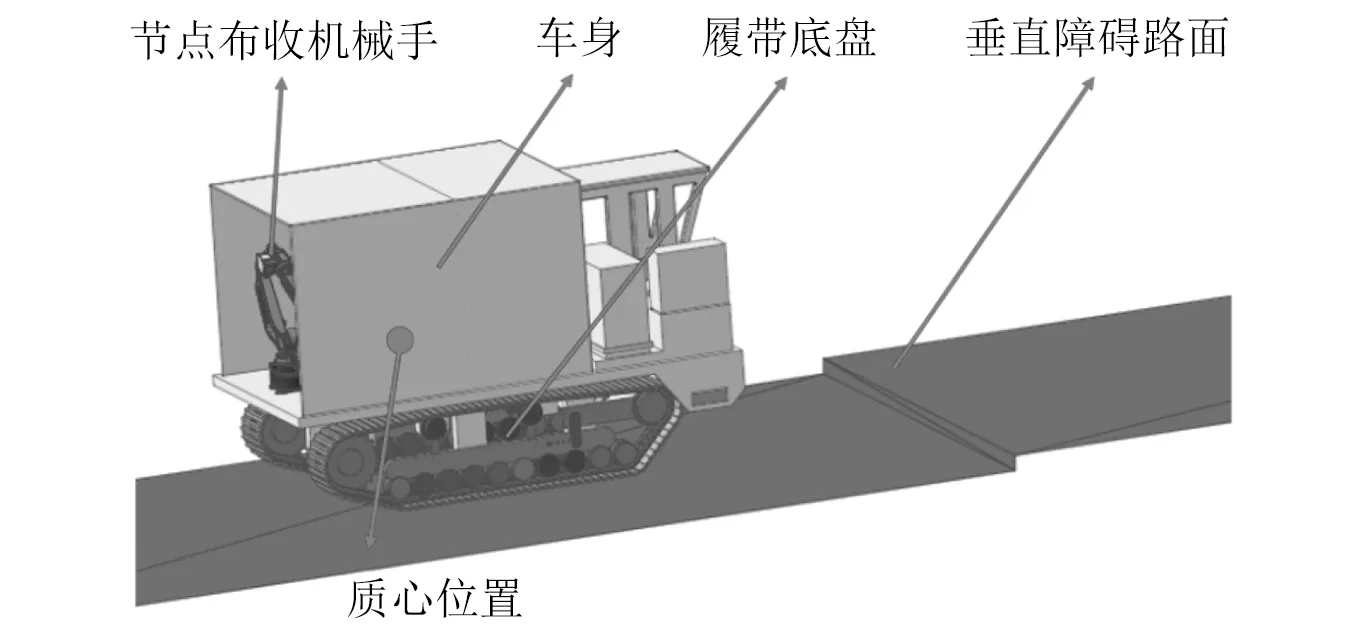
图2 整车动力学模型Fig.2 Model of vehicle dynamics
1.2 整车技术参数与边界条件设置
物探节点布收车整车包含履带底盘、驾驶室、机械手、节点料库、箱体、供电设备、控制箱等,主要技术参数如表2所示。
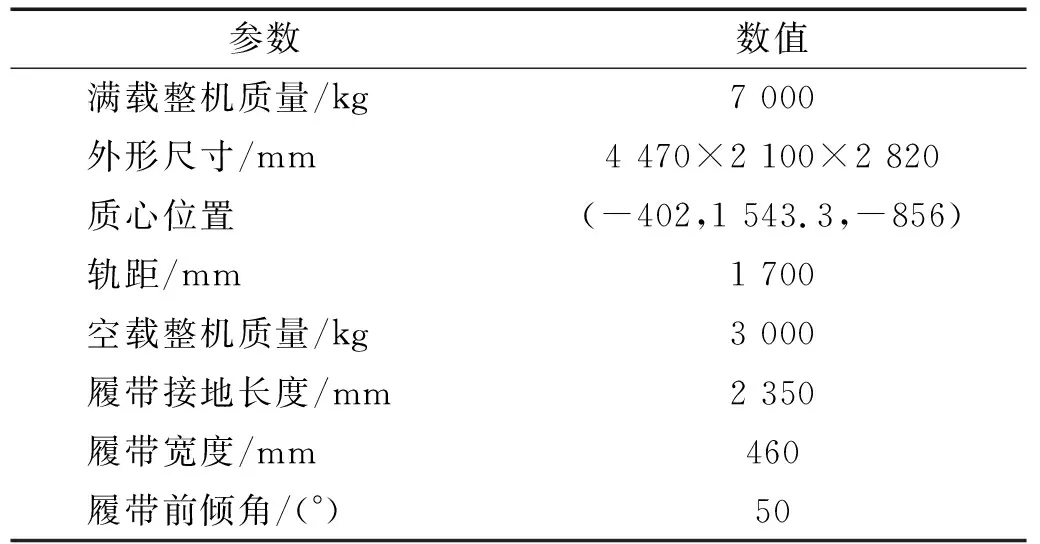
表2 整车技术参数Tab.2 Technical parameters of vehicle
为了更真实地模拟实际作业工况,将车速设置为低速3 km/h,地面设置为砂土,障碍物高度设置为150 mm,履带张紧力设置为车重的70%,仿真时间设置为15 s,步数为500步。
1.3 履带车辆越障力学分析
物探节点布收车越障时主要分为三个阶段:前端倾角处履带越障;车辆前端翘起,接地端履带越障[12];接地端履带落回水平面,直至完成越障。车辆以速度v越障时,越障前两个阶段底盘受力如图3所示。
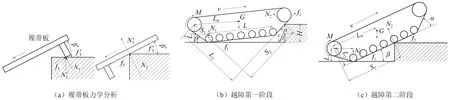
图3 履带底盘越障力学分析Fig.3 Mechanics analysis of crawler chassis obstacle crossing
履带板接触垂直障碍物时受力如图3(a)所示,不滑移时需满足
(1)
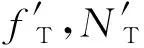
履带在第一阶段越障时受力如图3(b)所示,平衡时需满足
(2)
根据式(1)、式(2)可得出
(3)
履带在第二阶段越障时受力如图3(c)所示,平衡时需满足
(4)
根据式(1)、式(4)可得出
(5)
式中:G为底盘重力;N1,N2分别为后支重轮-地面与履带-障碍物支撑力;f1,f2分别为履带-地面和履带-障碍物摩擦力;L为接地长度;L0为质心-驱动轮间距;L1,L2分别为N1和N2与驱动轮中心的垂直间距;S1,S2分别为N1和N2与驱动轮中心的水平间距;α为前倾角大小;β为接地履带-地面夹角;H为障碍高度;θ为履带后角大小。
综上,车辆满足不滑移和平衡状态时可以顺利越障,在极限平衡状态时,履带接地端与地面之间存在最大夹角β,随着车辆的移动,瞬间落回地面时将产生巨大冲击,且与α,L,G等参数均有关。
2 车辆越障稳定性响应分析
物探节点布收车在越障工况承受巨大振动、冲击,对车体结构、车内设备和驾驶员的健康带来严重威胁。履带底盘行走装置各部件均以焊接、铰接的方式固定在机架的两侧主梁上,两者为一个整体,履带机架作为主要承载、受力部件,可以直接反映出车辆稳定性状态。
2.1 车辆越障动力学特性分析
2.1.1 不同路面激励下的车辆振动模型
复杂路况越障时车辆振动方向主要表现在垂向。假设z轴将车辆分为两部分,忽略侧摆振动;各轮系悬架的弹性特性、刚度和阻尼均相同;路面激励为随机激励,路面为刚体;对行驶速度为v的物探节点布收车,取静平衡质心G点作为动坐标系的远原点,建立车辆线性振动模型,如图4所示,zn为各支重轮的垂向位移;ln为支重轮与质心位置水平距离。
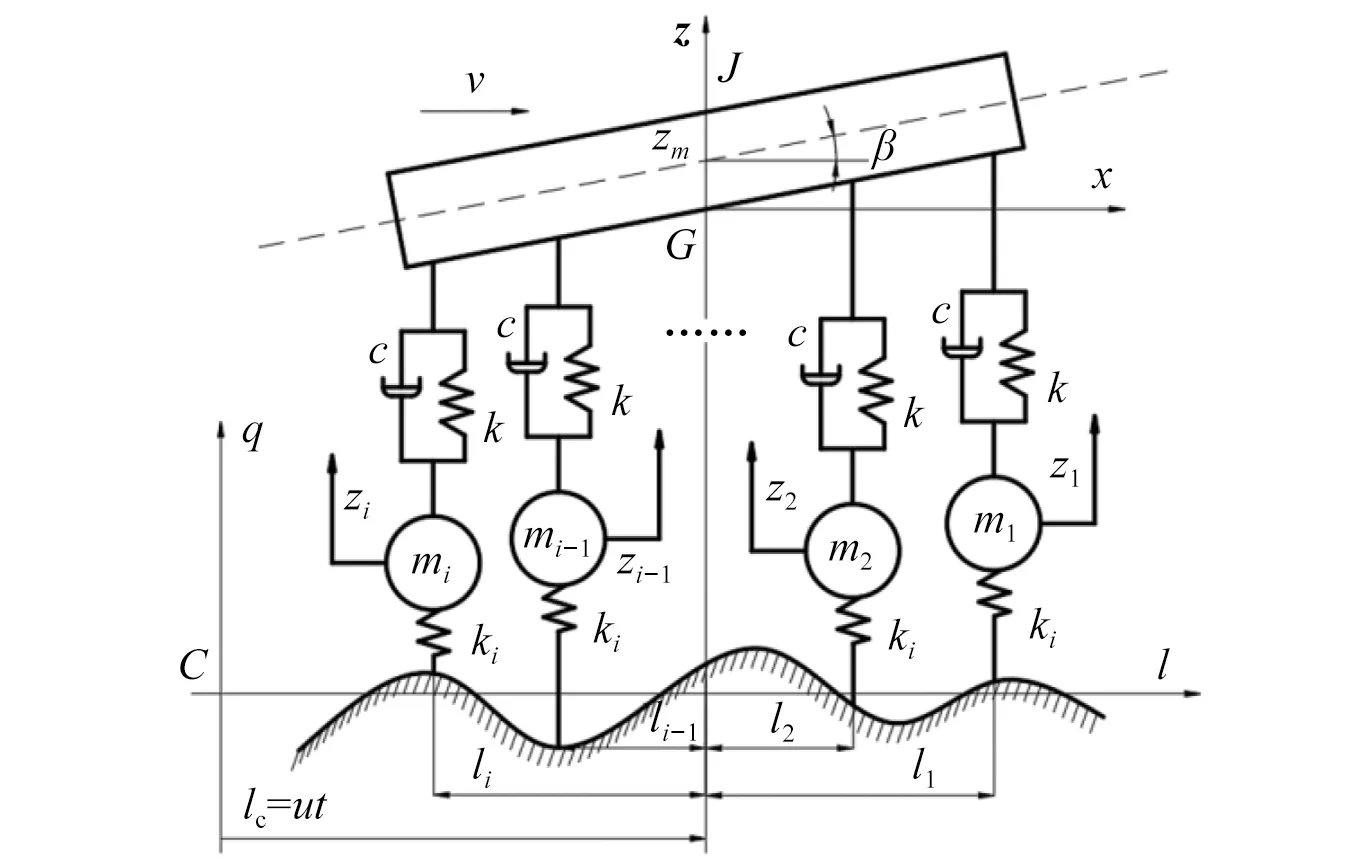
图4 车辆振动力学模型Fig.4 Mechanics model of vehicle vibration
车辆在路面激励q={q1,…,qi}作用下,其位移向量为z,建立车辆行驶过程中的动力学方程为
(6)
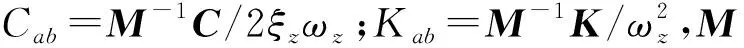
物探节点布收车在野外行驶时,激励q的相关元素与车速v存在函数关系,故车辆的振动z与ξz,ωz,v有关,当车体的固有频率与激励频率接近时,车辆的振动会更加剧烈。
2.1.2 不同越障阶段下整车动力学分析
如图5所示,将车辆越障全过程分为四个阶段进行分析。
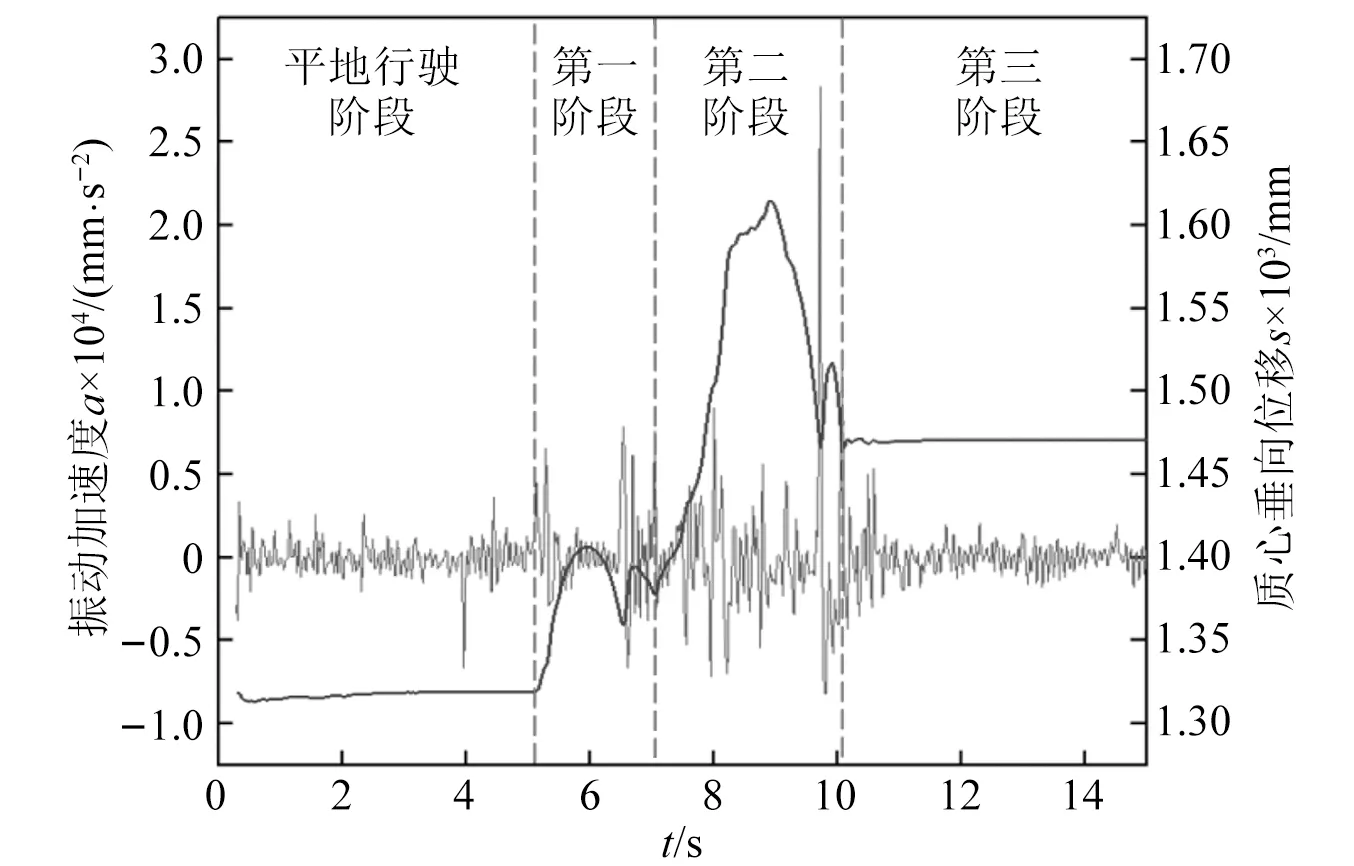
图5 车辆越障动力学分析Fig.5 Dynamics analysis of vehicle obstacle crossing
(1)在0~5.1 s时为车辆平地行驶阶段,其中0~3 s处于加速状态,后置驱动导致质心垂向位移略有上升,整体振动加速度较为平稳,车辆平稳行驶。
(2)在5.1~7 s时为前端倾角处履带越障,其中5.1~6 s质心位移上升后,又在6~6.5 s期间下降,是由于履带接触障碍物的瞬间,障碍物给车辆施加一个反作用力,导致前端翘起,随后又落回地面,在仿真中难以避免这种现象,此阶段最大振动加速度为7 861.4 mm/s2,车辆相对稳定。
(3)在7~10 s时为接地端履带越障,其中7~8.9 s时处接地端履带攀升阶段,在8.9 s时处于越障极限平衡,质心达到最高点,随后在速度作用下,车辆落回地面产生较大冲击,此时振动加速度a达到峰值28 320.1 mm/s2,车辆安全存在隐患。
(4)在10~15 s时为接地端履带落回水平面,随着履带后端与路面接触面积增加,质心垂向位移波动逐渐平稳,表明在10 s后车辆完成越障,与0~5.1 s期间的振动加速度波动相差不大,车辆越障全过程结束。
综上,物探节点布收车在越障第二阶段质心垂向位移和振动加速度曲线存在较大突变,稳定性较差,容易对底盘造成损伤。国内外缺少勘探车辆稳定性的评价标准,根据车辆的动力学曲线数据也难以评价车辆安全状态,故选择与行走装置固定的机架作为稳定性响应目标,通过机架所受应力情况来评判底盘的好坏。
2.2 履带机架瞬态响应分析
2.2.1 边界条件与激励载荷设置
底盘机架材料为Q345钢,屈服极限为345 MPa,安全系数取1.5,由此可以计算出机架的许用应力为230 MPa。车辆满载时为7 000 kg,根据前述动力学分析确定机架所受最大加速度为28 320.1 mm/s2,冲击时间为0.06 s,以此作为输入激励载荷。具体材料参数如表3所示。

表3 底盘机架材料(Q345B)参数Tab.3 Chassis frame material (Q345B)parameters
2.2.2 机架应力响应分析
由图6可知,机架应力主要集中在前横梁、中立柱、后立柱、后横梁与主梁连接处以及上层机架右梁前方的连接处,选取应力集中明显的A、B、C三区域进行分析。
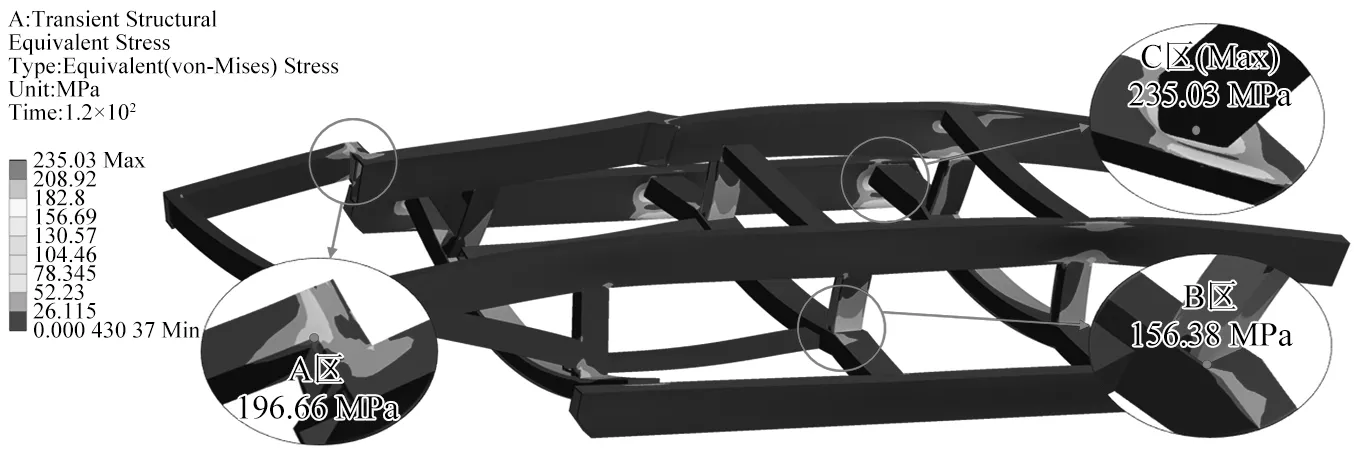
图6 底盘机架三区域瞬态响应Fig.6 Chassis frame three area transient response
(1)A区域中采用短空心方钢通过焊接方式对梁进行连接,主要承载驾驶室和发电设备,应力集中较为明显,最大应力为196.66 MPa,未超过许用应力,满足强度要求。
(2)B区域中中立柱为空心方钢,与之连接的中横梁为实心钢,故应力表现在立柱上,最大应力为156.38 MPa,未超过许用应力,满足强度要求。
(3)C区域中主梁采用空心钢,主要承载行走装置的轮系和上方箱体,最大应力为235.03 MPa,超过许用应力,机架存在过载、产生裂纹等危险,严重危害车辆安全。
根据上述底盘机架应力情况,发现在C区域连接处的最大应力超过许用应力,需要对底盘进行优化。目前底盘优化时多以机架为主,忽略了行走装置对其影响,故选择对行走装置进行结构优化,减轻越障冲击,保障车辆安全。
3 基于响应面法的履带底盘结构优化研究
以物探节点布收车的振动加速度标准差作为平顺性指标,振动加速度峰值作为冲击指标,对履带底盘的行走装置结构参数进行修改,利用响应面法找出最佳参数匹配来增强车辆越障稳定性和安全性。
3.1 履带行走装置自变量范围的选择
在确定前倾角范围时,以农用履带车、坦克、工程履带车作为参考;在确定履带张紧力时,根据文献[13-15],确定合理的张紧力区间;在确定履带接地长度时,前倾角的变化会导致支重轮轮系的移动,在满足行走装置导向轮和驱动轮轮心间距不变的情况下,轮系最后一个支重轮不与驱动轮发生干涉,在此区间选择接地长度。在满足车辆相关要求下,对履带行走装置自变量范围如表4所示。

表4 行走装置自变量范围Tab.4 Range of values of independent variables
3.2 响应面试验设计与结果
利用Box-Behnken进行试验设计,选取履带张紧装置张紧力F,履带行走装置前倾角θ以及履带接地长度L作为自变量,将车辆垂直方向的振动加速度标准差σ和垂向加速度峰值ae作为响应值。试验方案与结果如表5所示。
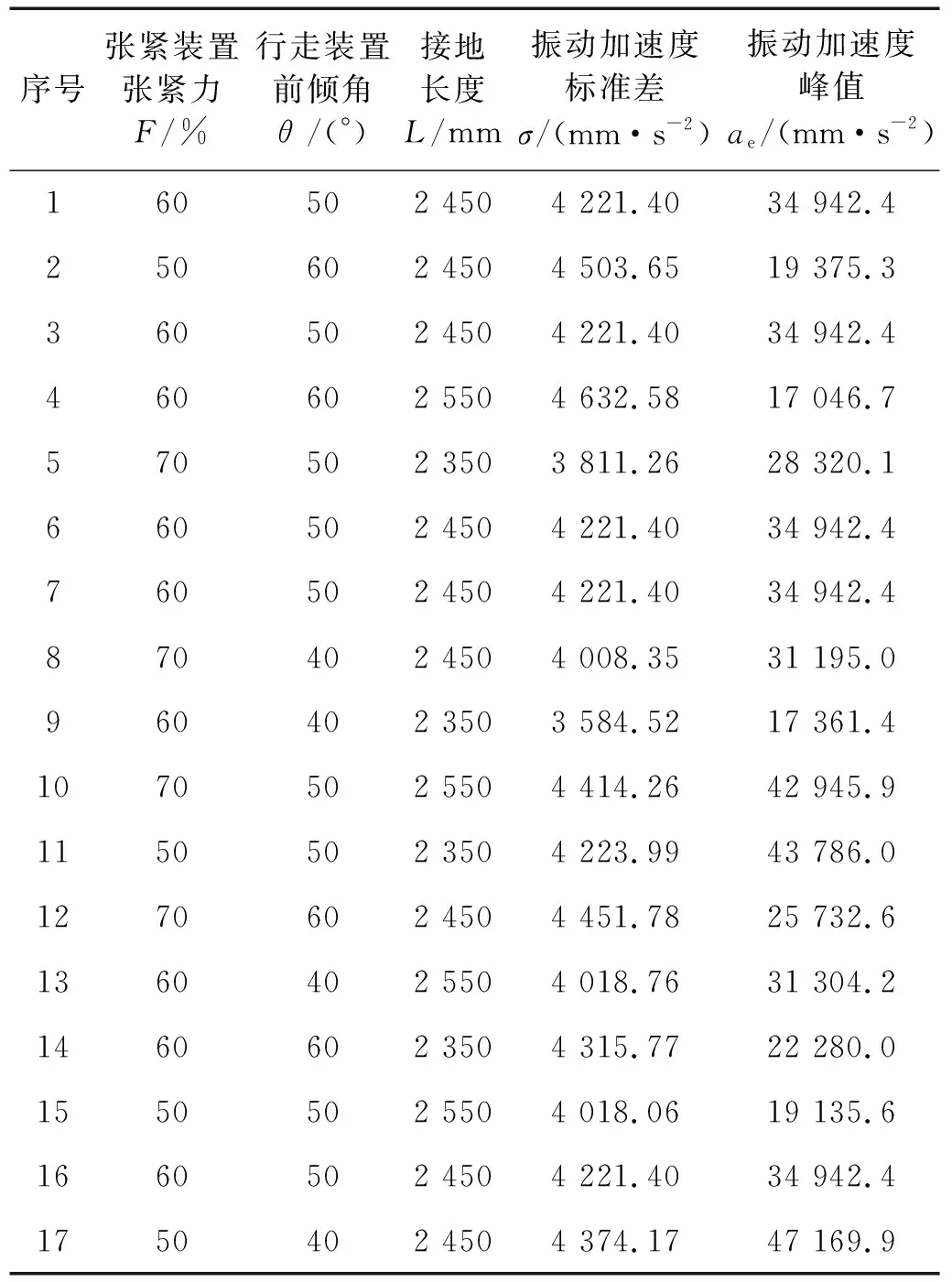
表5 响应面试验方案与结果Tab.5 Response surface test design and results
3.3 响应面模型的建立
3.3.1 回归方程的建立
将以上自变量和响应值进行二次回归拟合,得到车辆振动加速度标准差σ和加速度峰值ae的二阶回归方程,如式(7)、式(8)所示
σ=-2.796×104-651.36X1-64.89X2+41.68X3+
(7)
ae=-2.05×106-31 348.87X1+15 674.58X2+
2 164X3+55.83X1X2+9.82X1X3-4.79X2X3+
(8)
式中:X1为履带张紧力F;F2为履带行走装置前倾角θ;X3为接地长度L。
3.3.2 响应面模型误差分析
为了验证模型的精度,需要对其进行误差分析。响应结果中p≤0.05表示模型显著,精准度较好;反之精准度较差。表6为两响应值的精度分析,结果表明精度较高,可用于后续多目标优化求解。
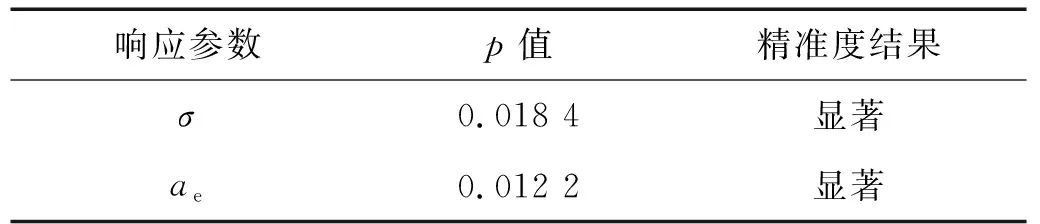
表6 响应面误差分析Tab.6 Error analysis of response surface
3.4 履带行走装置结构参数与响应值的规律分析
3.4.1 单因素与响应值的规律分析
根据物探节点布收车的垂向振动加速度标准差σ的二次回归方程,得到了单个履带行走装置结构参数与振动加速度标准差的规律曲线,如图7所示。
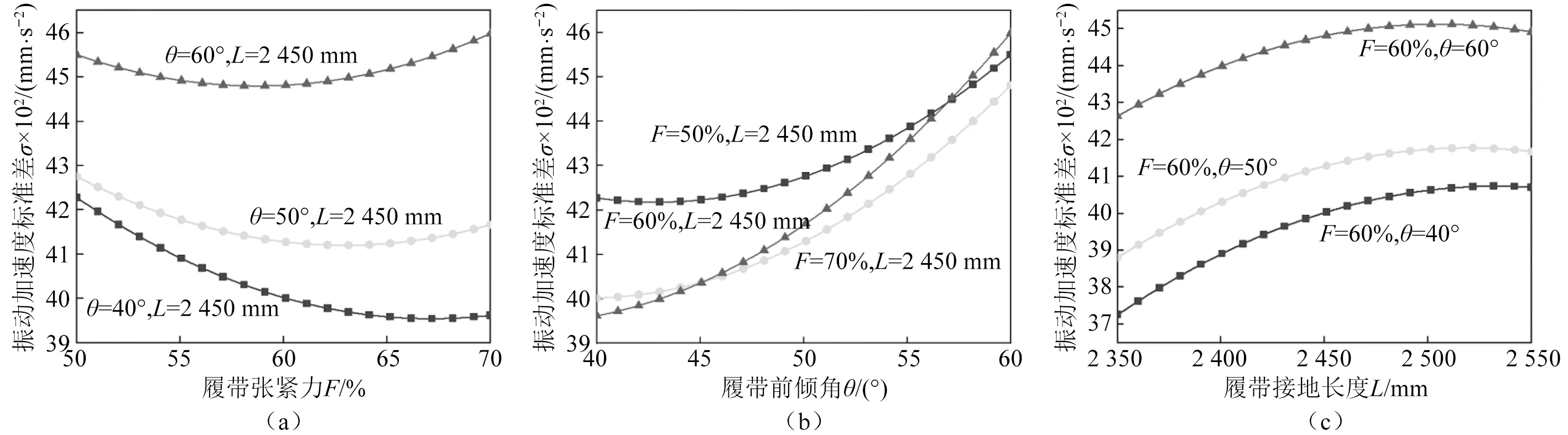
图7 行走装置不同参数对振动加速度标准差的影响Fig.7 Effect of different parameters of the travel device on the standard deviation of vibration acceleration
(1)分析图7(a)可知,车辆垂向振动加速度标准差随着履带张紧力的增大,呈先减小后增大的趋势,当履带前倾角θ为40°,50°,60°时,垂向振动加速度标准差在履带张紧力F分别为67.2%,62.9%,58.7%时达到最小值。随着履带前倾角θ的逐渐减小,振动加速度标准差在50%~70%的履带张紧力F范围内整体呈现减小趋势,说明履带前倾角的减小更有利于车辆的越障平顺性。
(2)分析图7(b)可知,车辆垂向振动加速度标准差随着履带前倾角θ的增大,呈逐渐增大的趋势。当履带前倾角θ=45.1°时,垂向振动加速度标准差在履带张紧力F=60%和F=70%时相同;履带前倾角θ=57°时,垂向振动加速度标准差在履带张紧力F=50%和F=70%时相同。实际设计底盘时,当履带前倾角θ<45.1°时,选择履带张紧力F=60%,具有更好的平顺性;当履带前倾角θ>45.1°时,选择履带张紧力F=70%,具有更好的平顺性。
(3)分析图7(c)可知,车辆垂向振动加速度标准差随着履带接地长度的增大,呈先增大后减小的趋势,履带接地长度L越小,车辆平顺性越强,这是因为车辆在越障时,较短接地长度的履带可以更快地落到障碍上。因此在车辆满足接地比压的情况下,可以选择较短的接地长度。
同理,根据物探节点布收车的垂向振动加速度峰值ae的二次回归方程,得到了单个履带行走装置结构参数与振动加速度峰值的规律曲线,如图8所示。
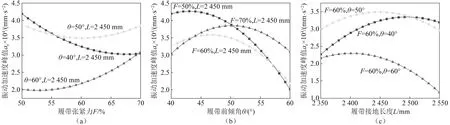
图8 行走装置不同参数对振动加速度峰值的影响Fig.8 Effect of different parameters of the travel device on the peak vibration acceleration
(1)分析图8(a)可知,不同的履带前倾角θ,对应的履带张紧力F与垂向振动加速度峰值ae的变化规律存在差异性,如当θ=40°时,ae的最小值出现在高张紧力区域,而当θ=50°时,ae的最小值在车辆原有张紧力60%左右,当θ=60°时,ae的最小值出现在低张紧力区域。因此车辆根据行走装置前倾角的大小来调整履带张紧力,可以改善车辆所受冲击情况,增强底盘寿命。
(2)分析图8(b)可知,在履带张紧力F=50%和F=60%时,振动加速度峰值ae的最小值均处于最大前倾角θ=60°处;当F=70%,ae随着前倾角的增大,先增大后减小,在前倾角40°和60°具有相同的振动加速度峰值。在设计行走装置结构参数时,不能追求大张紧力所减小的冲击性,需同时考虑行驶平顺性。
(3)分析图8(c)可知,不同的履带张紧力F,对应的履带接地长度L与振动加速度峰值ae的变化具有较大差异,当θ=40°,L=2 350 mm时,ae出现最小值,而当θ=60°,ae最小值出现在L=2 550 mm,这是由于物探节点布收车质心位置处于后方,在改变前倾角大小的同时,接地履带末端相对于质心的位置也随之改变,导致车辆在越障后所受到的冲击性差异较大。
3.4.2 两因素在交互下与响应值的规律分析
根据物探节点布收车的垂向振动加速度标准差σ的二次回归方程,得到了两个履带行走装置结构参数在交互下与振动加速度标准差的规律曲线,如图9所示。
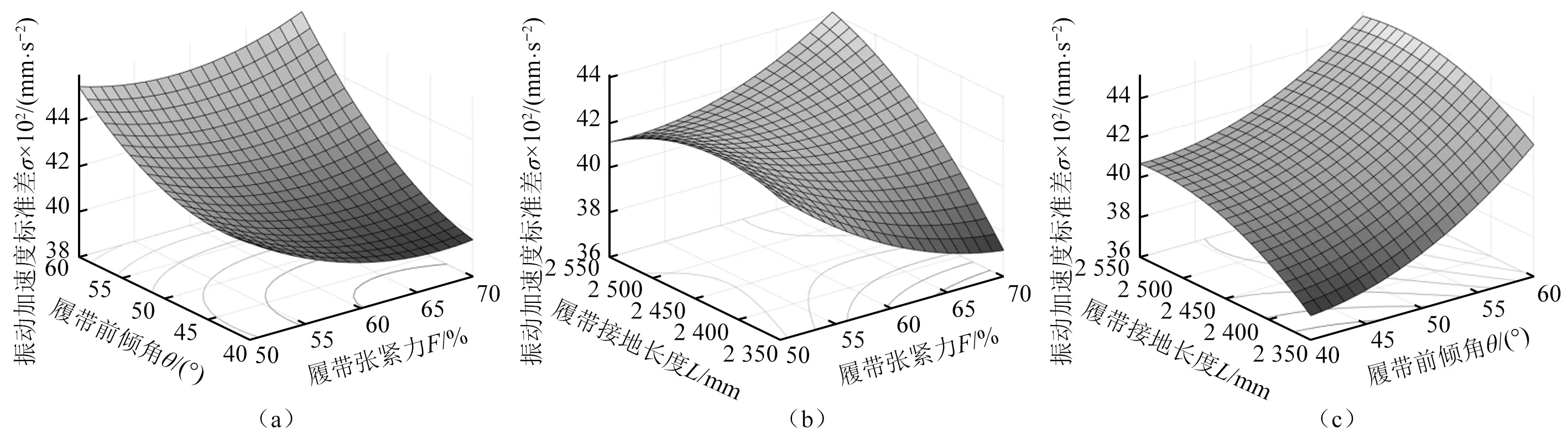
图9 行走装置多参数交互下对振动加速度标准差的影响Fig.9 Effect of multiparameter interaction of travel devices on the standard deviation of vibration acceleration
分析图9(a)可知,增大履带张紧力并减少履带前倾角可以有效地减小车辆垂向振动加速度标准差;分析图9(b)可知,增大履带张紧力、减小履带接地长度或减小履带张紧力、增大履带接地长度,才会减小振动加速度标准差;分析图9(c)可知,只有同时减小履带接地长度和履带前倾角才会降低振动加速度标准差。根据交互效应分析可知,较小的履带前倾角和履带接地长度可以有效增加车辆越障稳定性。
分析图10(a)可知,只有同时增大履带前倾角和减小履带张紧力,或同时减小履带前倾角和增大履带张紧力才能降低振动加速度峰值,且前者交互作用下降低地更明显;分析图10(b)可知,只有同时增大履带接地长度和减小履带张紧力,或同时减小履带接地长度和增大履带张紧力才能降低振动加速度峰值,两者具有相似的振动加速度峰值;分析图10(c)可知,当履带前倾角范围为42°~50°,2 420~2 510 mm时,振动加速度峰值具有较大峰值,行走装置结构参数应尽量避开此区间。根据交互效应分析可知,履带张紧力、履带前倾角以及履带接地长度均对振动加速度峰值有较大影响,其中增大前倾角可以有效降低振动加速度峰值。
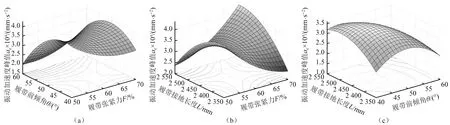
图10 行走装置多参数交互下对振动加速度峰值的影响Fig.10 Influence of multiparameter interaction of travel devices on peak vibration acceleration
3.5 履带行走装置最佳结构参数的确定
对履带行走装置的垂向振动加速度标准差和振动加速度峰值进行多目标优化,对两目标分配不同权重因子,将权重因子与两目标值的乘积进行求和,和的最大值即为最优解,计算公式如式(9)所示
(9)
式中:(α1,α2)为σ(x)和ae(x)的权重值;xiL,xiU(i=1,2,3)分别为履带行走装置各结构参数变量的上下限。
同时为了避免数值集中或某个值较大,采用离差标准化的方法对原始数据进行线性变换,将响应值映射在[0,1]区间内,有效消除两数量级之间差异,使优化结果更准确,其转换式(10)如下所示,图11列举了三种权重组合下的最优解集。
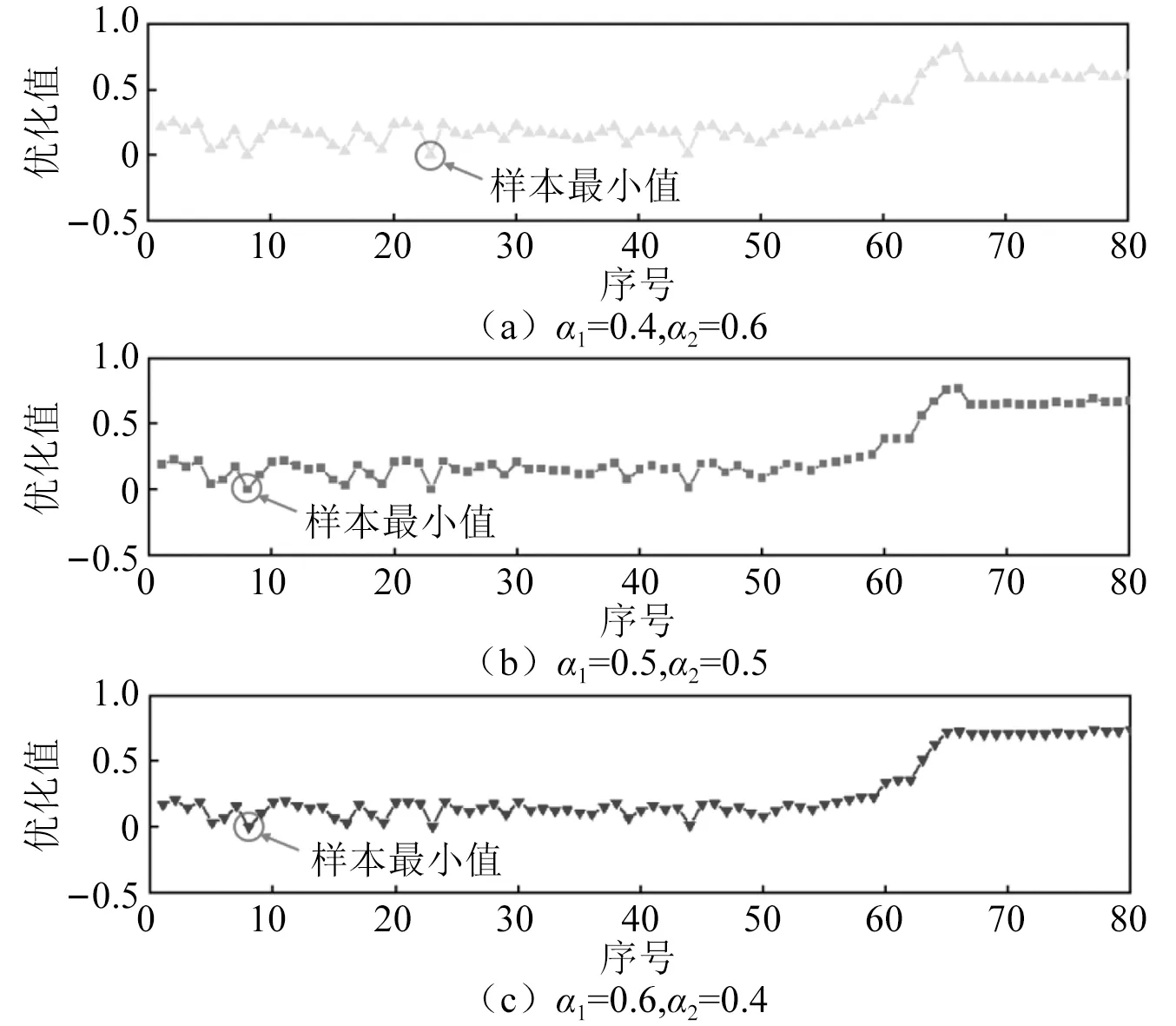
图11 不同权重组合下的最优解集Fig.11 The optimal solution set under different combinations of weighting factors
(10)
式中:xmin为样本最小值;xmax为样本最大值。
分析图11可知,当α1=0.4,α2=0.6时,最优解的序号为23;当α1=0.5,α2=0.5时,最优解的序号为8;当α1=0.6,α2=0.4时,最优解的序号为8。在对物探节点布收车进行履带底盘设计时,若较注重野外整体稳定性,可以选择序号8对应的行走装置结构,若更注重减少野外越障时所受到的冲击时,则可以选择序号23对应的行走装置结构。而在实际作业过程中,布收地震节点时需穿越多种复杂地形,减少整车冲击,保护车内设备安全为首要设计要求,故选择序号23对应的行走装置结构,即履带张紧力F=69%,行走装置前倾角θ=42°,接地长度L=2 353 mm作为最优结构。
4 底盘优化前后稳定性对比分析
优化后的履带行走装置结构在越障过程中振动加速度标准差为3 507.5 mm/s2,最大振动加速度峰值为ae=12 055.5 mm/s2,以此加速度为输入条件对机架进行瞬态响应分析,由图12可知,A区域的最大应力为180.89 MPa,比优化前应力减少了8.02%;B区域的最大应力为147.01 MPa,比优化前应力减少了9.37%;C区域中的最大应力为220.42 MPa,比优化前应力减少了6.22%,满足了强度要求。三区域的应力均有不同程度的减少,有效地增加了机架的可靠性,保障了车辆的平稳、安全运行。表7为优化前后数据对比。
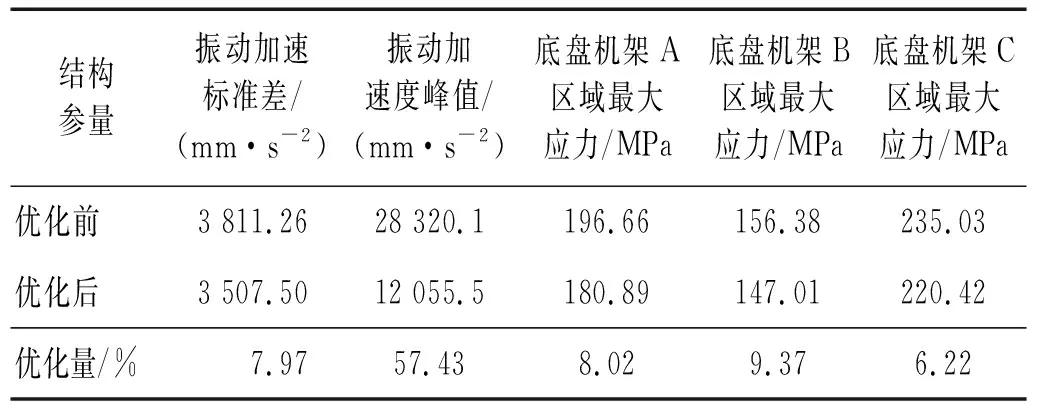
表7 底盘优化前后数据对比Tab.7 Chassis optimization before and after data comparison

图12 底盘机架优化后瞬态响应Fig.12 Transient response after chassis frame optimization
5 结 论
(1)建立了物探节点布收车的履带底盘行走装置的拓扑结构图和整车动力学模型,分析了车辆在复杂路况下越障过程中的前两个阶段的力学特性,得到了车辆在越障过程中的接地履带-地面夹角β决定了最大振动加速度的大小,且与履带行走装置的前倾角α、接地长度L、重心位置G等因素有关。
(2)建立了不同路面激励下的车辆振动模型,开展了车辆的越障稳定性响应分析,根据整车动力学分析,将响应值作为输入条件,对履带机架进行瞬态分析,结果表明:机架C区域最大应力为235.03 MPa,超过许用应力,存在安全隐患。
(3)以平顺性和冲击作为指标,开展了履带底盘的响应面优化试验研究,通过分配不同权重值,确定了行走装置最优结构为履带张紧力F=69%,行走装置前倾角θ=42°,接地长度L=2 353 mm,优化后的物探节点布收车在越障时平顺性增加了7.97%,冲击减少了 57.43%,履带机架A,B,C区域的最大应力分别减少了8.02%,9.37%,6.22%,均满足强度要求。

