地震作用下基于性能的中小跨径梁桥横向支承约束系统设计优化

鲁冠亚, 王克海, 吴 刚, 张熙胤

(1. 兰州交通大学 土木工程学院,兰州 730070; 2. 交通运输部公路科学研究院,北京 100088; 3. 华东交通大学 土木建筑学院,南昌 330013)

中小跨径梁桥的抗震设计是一个高度迭代和繁琐的仿真计算过程。以往的研究通常使用确定性方法进行桥梁抗震设计的优化[1-4]。它们的缺点是:①通过使用地震反应谱或少量地震动时程记录的确定性分析方法进行桥梁支承约束系统的优化设计,无法考虑地震动的不确定性;②以往研究的抗震设计一般以特定结构为研究对象,且优化指标不具有通用性,结构一旦发生变化,就将引起设计过程的重复。

为克服确定性方法的不足,近年来,研究人员基于性能的抗震设计(performance based seismic design,PBSD)框架进行了一系列的结构抗震设计,例如:Mackie等[5]采用非线性函数形式表征桥梁设计参数和桥墩损伤概率的关系;Zhang等[6]通过计算公路桥梁系统的易损性均值强度研究了不同支座的最优设计参数。虽然这些研究是关于PBSD的,但都只是经过重复计算得到指定设计参数下结构的损伤概率,未形成一个完整的优化过程。万华平等[7]基于桥梁系统地震易损性,采用高斯过程模型对一座三跨连续梁桥的隔震支座进行了优化设计。由于该研究采用地震动强度指标(intensity measure, IM)建立易损性函数,对于支承系统设计参数不同的桥梁,易损性函数的不同导致了桥梁抗震性能指标的改变,这就为优化程序的目标函数带来困难。Franchin等[8]基于极限状态的年平均超越概率和等位移原则,使用基于梯度的搜索算法优化了钢筋混凝土结构的设计参数。Xie等[9]以一座典型的预应力连续梁桥为例,以桥墩位移延性和支座位移为优化目标,基于遗传算法建立了抗震装置参数的多目标优化程序。梁瑞军等[10]采用墩底剪力之和为目标函数,基于零阶优化算法,对曲线梁桥的铅芯橡胶支座力学性能参数进行了优化。上述研究在PBSD框架中采用智能算法进行优化设计,但是提出的方法仅针对特定桥梁,未能同时考虑线路区域中具有不同配置的桥梁。

本文基于区域线路中具有不同结构配置的中小跨径梁桥群组,考虑地震动的不确定性,选用铅芯橡胶支座,在PBSD框架下进行桥梁群组支承约束系统横桥向的抗震性能优化设计。通过logistic回归获得工程需求参数(engineering demand parameter, EDP)和损伤概率之间的关系,使得具有不同支承约束系统设计参数的桥梁产生一致的易损性函数,以此推导适用于桥梁群组的统一级系统性能指标修复成本比(repair cost ratio, RCR)作为优化目标函数,建立基于遗传算法的桥梁群组抗震性能优化程序,并验证所提优化程序的有效性。

1 基于性能的桥梁群组支承约束系统设计优化程序

基于性能的抗震设计需要确定以下几组关系:①损伤指标(damage measure,DM)与EDP,该组关系由易损性推导;②EDP与IM,该组关系由概率地震需求模型表示;③设计参数与EDP,该组关系由有限元计算实现。优化设计的关键就是通过优化设计参数控制EDP满足性能目标。在确定采用的桥梁支座类型的基础上,本文建立基于性能的桥梁群组支承约束系统设计参数的优化程序,具体包括以下3个步骤:

步骤1建立EDP条件下的桥梁构件易损性。以线路中的桥梁群组为研究对象,对初始设计桥梁的地震响应建立EDP条件下的易损性函数。有研究证明在特定桥梁中,每级IM下EDP分布的方差对于不同的支承系统参数可保持相同,并且能够以中值EDP为条件建立统一的易损性函数[11]。这样可以允许设计者每次考虑新设计时直接进行重复迭代的过程,能够显著提高桥梁抗震设计效率。

步骤2推导统一系统级性能指标。桥梁抗震性能应同时关注不同构件的响应,使得桥梁系统的抗震性能达到最优。选择能够直接反映系统级抗震性能的指标作为优化程序的目标函数是基于性能的抗震设计优化的基础。

步骤3基于遗传算法优化支承约束系统设计参数。近年来,包括遗传算法在内的智能算法在结构工程的优化中得到了显著应用,能够为各种工程优化问题提供解决方案[12-15]。因此,采用遗传算法可为支承约束系统设计参数的优化提供一个新途径。

1.1 EDP条件下的桥梁构件易损性建立

按下列步骤建立EDP条件下桥墩和支座的易损性函数:

步骤1进行桥梁支承约束系统的初始设计,对生成的“桥梁—地震动”样本进行非线性动力时程计算,获取最不利的桥墩位移延性需求幅值(μd)和支座位移需求幅值(db);

步骤2根据桥墩和支座的能力模型,在指定极限状态(limit state, LS)下,构件的能力值与步骤1计算的需求值进行比较,获得该极限状态的二元安全—失效(0—1)向量;

步骤3用EDP替代IM,基于logistic回归[16-17]建立损伤概率与EDP以及各桥梁属性的关系,见式(1)

(1)

式中:kedp和kj(j= 1,…,n)分别第k个构件的工程需求参数和各输入属性的对数回归系数;k0为回归截距;x1,…,xn为各输入属性。

上述过程分别获得了桥墩和支座的DM与EDP关系,只能反映构件的抗震性能,并不能表征桥梁系统的抗震性能。将其直接作为优化程序的目标函数时,优化程序为多目标优化程序。由于多目标优化问题不存在唯一的全局最优解,且求解过程较为复杂。所以,可以选择能够直接反映系统级抗震性能的指标作为优化程序的目标函数。

1.2 统一系统级性能指标的推导

在建筑结构系统中,为了反映系统的抗震性能,HAZUS[18]采用RCR作为性能指标评价结构系统的抗震性能[19]。RCR为不同IM级别下构件的修复成本与重建(更换)成本的比值,为结构系统级的损伤提供了一种有力的量测方式,可利用构件级易损性函数推导。仅考虑桥梁系统为最不利桥墩和支座构成时,桥梁系统的RCR可表示为

(2)

式中:η为桥梁系统的RCR;c为桥梁构件的重建或更换成本;下标col和bea分别为桥墩和支座;di为构件损伤率,定义为损伤极限状态i的损伤百分比,根据HAZUS建议按表1取值。i=0, 1, 2, 3分别对应轻微、中等、严重损伤和倒塌极限状态。

pi为桥梁构件处于损伤极限状态i的概率,可以通过构件易损性分析按式(5)计算得到

(3)

式中,P为构件易损性。

当以桥梁需求μd和db为条件时,能够证明推导的RCR是关于μd和db的均匀函数曲面,可表示为

η=f(μd,db)

(4)

因此,式(4)可以作为桥梁抗震性能优化的目标函数。

1.3 基于遗传算法的支承约束系统设计参数优化程序

由1.2节推导出桥梁群组的系统级性能指标RCR可以容易地纳入到PBSD框架中进行桥梁支承约束系统参数的优化。例如,设计人员可以指定在50年内超越概率为10%的设防水准下,将桥梁的RCR控制在5%以内。由于设计过程存在多次的试算过程,所以,应采用智能快速的迭代过程找到符合设计目标的支承约束系统参数。

本节建立了基于遗传算法的中小跨径梁桥抗震性能优化程序,以RCR为优化过程的目标函数。该优化程序为混合程序,其中OpenSees[20]非线性时程分析提供桥梁地震响应,在Matlab上利用遗传算法的极值寻优能力,求得非线性映射的极小值点,程序流程如图1所示。

该程序前一部分非线性时程计算提供了优化程序所需的初始种群,在后一部分中,遗传优化过程在对种群进行初始化之后,由适应度函数经过选择、交叉、变异,产生能够具有更好设计的子代总体,直到找出最优抗震性能设计参数后退出[21]。该程序中采用式(4)推导的系统级性能指标RCR作为遗传算法的适应度函数,它统一考虑了桥墩位移延性和支座位移,促进了优化过程,代替了复杂的多目标优化程序的实施。

下面以汶马高速公路中的简支梁桥群组为例,选用铅芯橡胶支座,采用该程序对桥梁横桥向的抗震性能进行优化,确定具有最优抗震性能的支承约束系统参数。

2 简支梁桥群组的数值模拟和地震动选取

统计汶马高速公路中桥梁的基本信息显示该线路主线桥梁为简支梁桥,一联桥梁最常用的跨数为2跨、3跨和4跨。以一联桥梁进行地震响应分析,具有三种边界情况,即:两侧为相邻桥跨,一侧为相邻桥跨一侧为桥台以及两侧为桥台,依次记为A,B和C。简支梁桥采用预制的预应力T梁,主梁架设就位后进行翼板及横隔板间的钢筋连接和湿接缝混凝土的浇筑,一联孔跨间桥面连续。简支梁每个小T梁下设置支座,放置在有盖梁的双柱墩上。桥墩基础采用柱式桩基础,桩基础顶部设置地系梁,并且相比于桥墩截面增加了保护层厚度,桥梁结构立面如图2所示。

简支梁单跨跨径一般为30 m和40 m,70%桥梁采用标准12 m梁宽,其他桥梁的梁宽均匀分布于8～24 m。统计计算显示桥墩高度和纵向钢筋配筋率服从对数正态分布,配箍率的概率密度图具有双峰性。墩柱直径与跨径、柱高相关,经统计分析建议将柱径分为三类:小柱径(<1.6 m)、中等柱径(1.6～2.0 m)与大柱径(>2.0 m)。跨径30 m可作为小柱径和中等柱径的分界线,小于30 m采用小柱径,大于30 m采用中等柱径;跨径30 m处,进一步采用柱高分类,小于18 m采用小柱径,大于18 m采用中等柱径。仅当主梁宽度大于18 m时采用大柱径。桥墩高度的纵向布置分为等墩高布置(Ⅰ)和非等墩高布置(Ⅱ)两类。此外,该线路多经过横坡地形,双柱墩的两个柱高一般不相等,统计了横向柱高比。该线路桥台主要采用桩柱式桥台,其地震作用下的响应包括台背填土的土压力响应和桥台构件本身的响应。根据区域场地的土层情况,由“m”法[22]计算桩基的平动刚度和转动刚度,其刚度值服从对数正态分布。联端伸缩缝为16 cm或8 cm。文献[23]详细叙述了桥梁群组的几何、材料和结构属性统计过程,其结果如表2所示。

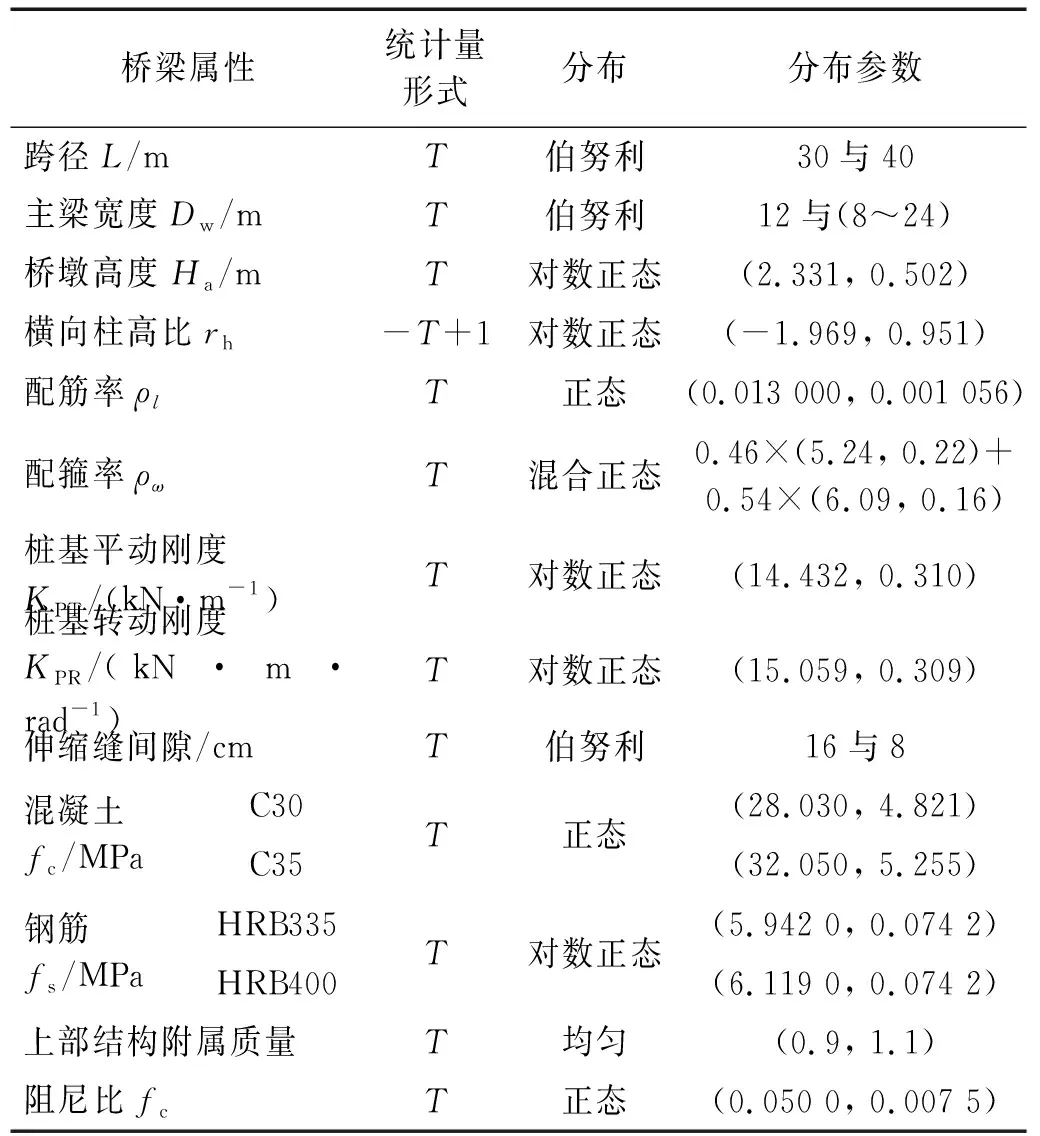
表2 桥梁群组属性统计分布Tab.2 Statistical distribution of the bridge attributes

为形成一联桥梁的配置,采用拉丁超立方抽样(Latin hypercube sampling,LHS)模拟概率分布函数中的可能值生成桥梁总体,以参数化建模方式在有限元平台OpenSees建立桥梁的三维数值计算模型,如图3(a)所示。主梁采用弹性梁单元模拟,质量分布在沿主梁中心线的节点上,与支座节点之间采用刚臂连接。弹塑性纤维梁单元模拟桥墩,混凝土和钢筋纤维分别采用Mander模型和双折线模型,如图3(b)所示。桥台上的被动土压力采用Shamsabadi等[24]提出的双曲线模型,主动土压力采用三折线模型,分别由HyperbolicGapMaterial材料和Hysteretic材料实现,并将材料属性赋予零长度单元,如图3(c)所示。采用具有线弹性材料的零长度单元模拟桩基。由具有ElasticPPGap材料属性的零长度单元模拟伸缩缝,如图3(d)所示。

铅芯橡胶支座的拟静力试验结果表明它具有较为稳定的滞回耗能特性[25],作为一种有效的隔震装置普遍用于高速公路中小跨径梁桥上。所以,本文采用铅芯橡胶支座对桥梁的抗震性能进行优化设计。根据规范建议,铅芯橡胶支座的恢复力模型可采用双线性,如图3(e)所示。图3(e)中:qb为支座屈服强度;k1,b和k2,b分别为支座屈服前刚度和屈服后刚度;采用Bouc-Wen单元对恢复力模型进行模拟。

在地震作用下,中小跨径梁桥在横桥向易发生主梁的显著移位,故通常在横桥向设置钢筋混凝土挡块来限制上部结构位移。汶川地震中,梁式桥挡块发生较为严重的震害,在简支梁桥中尤为突出,发生挡块破坏数量多达720组,占调查桥梁的16.8%,该比例与支座破坏率及主梁移位率相近。因此,挡块是横向支承约束系统的组成部分,在桥梁的地震响应分析中不可忽略[26]。

徐略勤等[27]结合中国钢筋混凝土挡块的构造特点和试验现象,建立了挡块的非线性分析模型,如图3(f)所示。图3(f)中:A,B,C,D是4个关键点,分别对应挡块的剪切钢筋发生屈服、混凝土剪切强度达到峰值、混凝土开裂失效和剪切钢筋断裂;Vy,Vn,Vd与Vu为特征强度; Δy,Δn,Δd与Δu为特征变形,详细参数计算可参考徐略勤等的研究。在OpenSees中,采用Multilinear材料属性分别模拟混凝土和钢筋的贡献,将材料属性赋予零长度单元,由两个单元的并联实现挡块的滞回特性,该并联组合体再与一个具有较大刚度的碰撞单元串联,考虑挡块与主梁的碰撞效应。

为了纳入地震动的不确定性,获得较为广泛的地震动强度,依据Baker等[28]提出的原则选择160条地震记录,所选地震记录的均值反应谱相当于线路桥梁群组所在场地的50年内超越概率5%的规范反应谱,如图4所示。为确保桥梁结构进入显著的非线性阶段,将地震动的峰值强度按比例进行缩放,扩展为480条地震动。

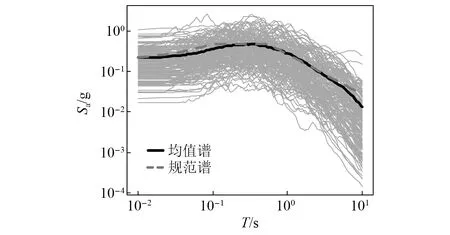
图4 地震动反应谱Fig.4 Ground motion spectra

3 简支梁桥横桥向抗震性能优化

3.1 EDP条件下桥梁构件级易损性函数

为了建立EDP条件下桥墩和支座的易损性,首先定义其损伤极限状态。采用Pushover分析定义桥墩的损伤极限状态,如图5所示。根据Pushover分析的结果,应用弹性网回归,由桥墩属性参数回归建立桥墩的能力模型,同时计算屈服强度QC和弹性刚度K1,C。弹性网回归就是在多元线性模型的平均损失上加入一个惩罚项,避免模型“过拟合”,见式(5)。

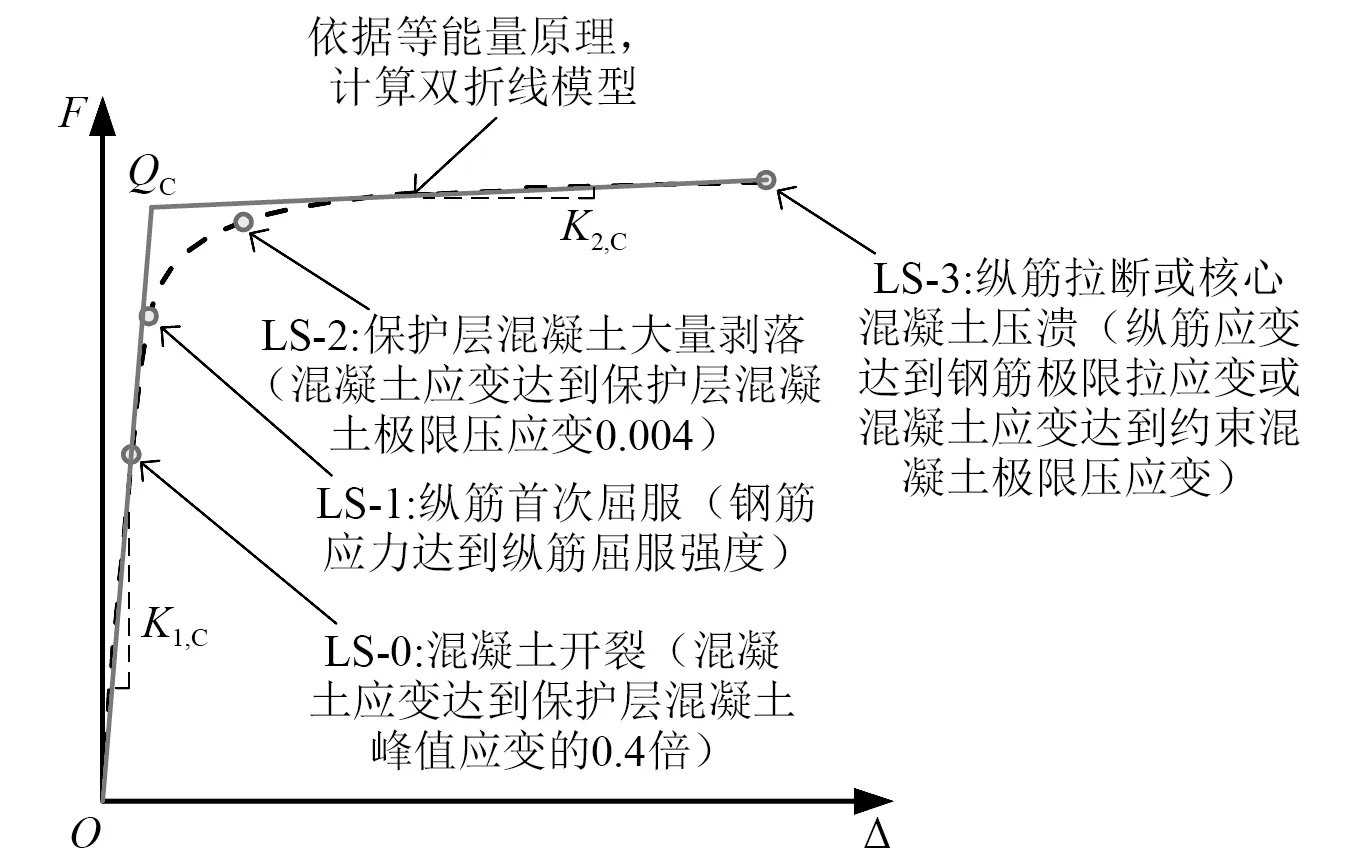
图5 桥墩的损伤极限状态Fig.5 Damage limit states of piers

(5)

式中:βj为桥墩属性的回归系数; 输入参数包括Ha与rh,ρl与ρω,KPT和KPR,fc和fs,Dw,L与Mass;λ为回归模型超参数,用于调整平均损失项与惩罚项之间的关系,经分析后取0.001 5;α为L2范数与L1范数的权重系数,本文取0.5。限于篇幅,仅显示回归模型的判定系数R2均大于0.8,模型具有良好的预测能力。

结合桥梁震害和JTG/T 2231-01—2020《公路桥梁抗震设计规范》定义铅芯橡胶支座支承系统横桥向的损伤极限状态,如表3所示。表3中:ESS为等效剪切应变,即支座位移与支座橡胶层总厚度的比值;Gapsk为挡块与主梁的间距。

表3 支座约束系统的损伤极限状态Tab.3 Damage limit states of bearing restraint system

对于本研究的设计优化问题,首先明确支承约束系统的设计参数。Zhang等和Xie等通过大量的隔震支座参数研究证明,对于不同类型的隔震支座,支座的弹性刚度K1,b对桥梁的抗震性能影响不大,在最优设计中应仔细选择屈服强度Qb和屈服后刚度K2,b。本文统计了汶马路中桥梁设计使用的钢筋混凝土挡块的尺寸和配筋情况,参考徐略勤等的研究计算并统计了图3(f)中4个关键点对应的特征强度与变形。发现挡块的弹性刚度Ksk服从对数正态分布,其对数均值和对数标准差分别为13.967 kN/m和0.328 kN/m;而各变形特征点主要集中于某个常数值,如表4所示。计算各特征强度发现,Vy可通过Ksk与Δy计算,而Vn和Vd与Vy具有很强的线性相关性,如图6所示。此外,Gapsk是影响其限位效果发挥的关键因素,统计显示原设计间隙均匀分布于5～8 cm。因此,挡块的优化参数可考虑为其弹性刚度和间距。

图6 挡块特征强度的确定Fig.6 Determination of characteristic strength of shear keys

表4 挡块特征变形Tab.4 Shear key characteristic deformation 单位: mm

由于不同高度的桥墩,其墩柱直径、配筋率和配箍率等有所差异,导致桥墩的QC和K1,C不同,而支座的优化参数是与桥墩的QC和K1,C相关的。所以,为了考虑桥墩的不同,支座的优化参数按Qb/QC和K2,b/K1,C进行取值。根据上述确定的参数,对简支梁桥群组设计三种初始方案,如表5所示。表5中:Qb=n·qb;K2,b=n·K2,b;n为桥墩上的支座总数;工况S,具有强隔震效应,Qb和K2,b分别占QC和K1,C的比例较小,支座强度和刚度小,主梁具有充分的横向运动空间,且挡块刚度偏小;工况M,具有中等隔震效应,Qb和K2,b与QC和K1,C相比,比例适中,主梁的横向运动空间约为一倍支座橡胶层总厚度,挡块刚度适中;工况W,具有弱隔震效应,Qb与QC接近,K2,b占K1,C比例较大,主梁的横向运动空间较小,挡块刚度大。可见,这三种初始设计涵盖了应有的设计效应范围。另外,对于K1,b的确定,结合铅芯橡胶支座规范K2,b/K1,b可取为0.15[29]。

表5 支座约束系统横桥向初始设计参数Tab.5 Initial design parameters of bearing restraint system in transverse direction

根据表2中简支梁桥的属性分布以及三种初始隔震设计,通过LHS生成480个具有95%保证率的桥梁样本,并与选择的地震动配对生成“桥梁—地震动”样本,由OpenSees进行非线性时程动力分析,记录最不利的桥墩位移延性幅值和支座位移幅值。根据1.1节步骤建立EDP条件下的易损性曲线,由logistic回归建立桥墩和支座的EDP与其损伤概率之间的关系。输入logistic回归模型的桥梁属性变量包括支承系统类型(BeaType,即表5中的设计工况)和边界类型(BouType),主梁的跨数(Nspan)、L和Dw,Ha、rh和墩高的纵向布置(Hlayout),ρl和ρω,KPT和KPR,fc和fs,Mass以及ξ。

以汶马路的典型桥梁为例,桥梁参数如表6所示,说明在支承约束系统的优化设计问题中采用EDP建立易损性的原因。将桥梁参数输入式(1)建立的易损性函数中,图7显示了该桥梁的桥墩和支座发生严重损伤时,以IM为条件的构件级易损性曲线。由图7可见,三种支承约束系统的设计工况在每个IM条件下的桥墩和支座的破坏概率是显著不同的。例如,强隔震可能会显著降低桥墩的响应,但会大大增加支座位移,在相同的地震动强度下,不同的支承约束系统设计将产生桥墩和支座的不同响应。

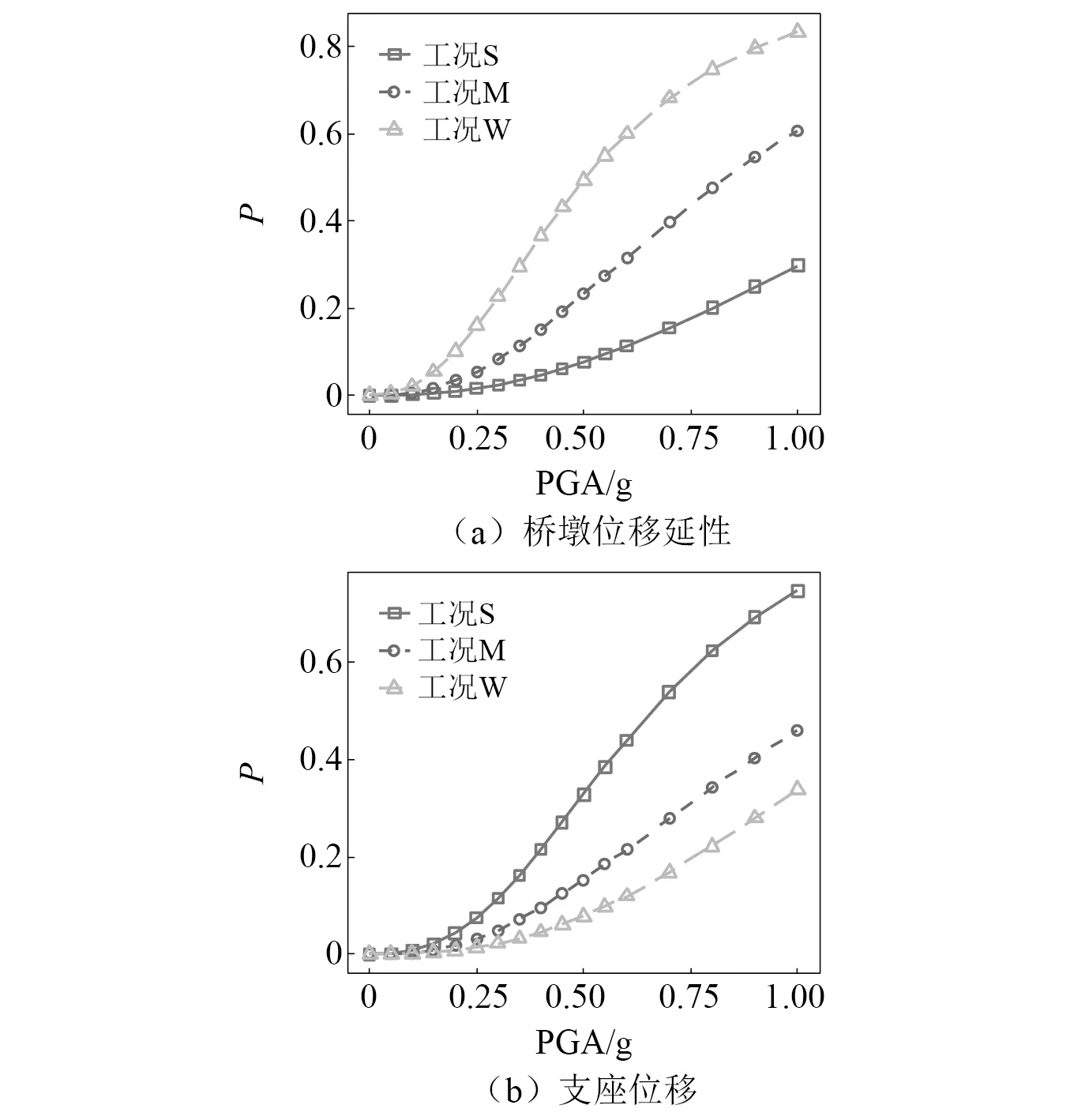
图7 IM条件下严重损伤状态的构件级易损性曲线Fig.7 Component-level fragility curves of severe damage state conditioned on IM

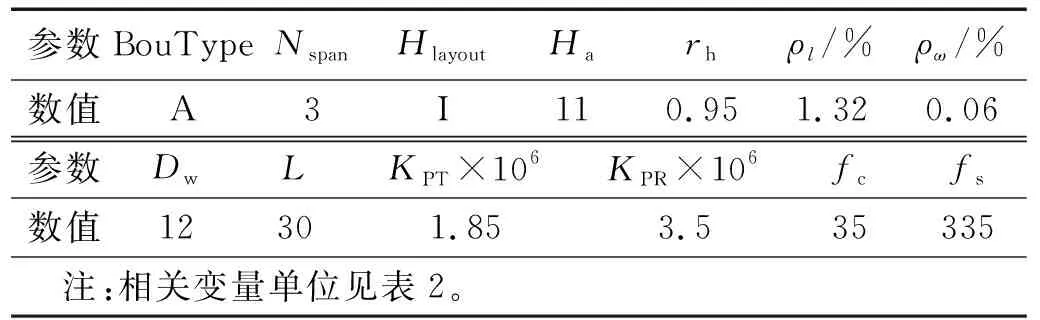
表6 案例桥梁参数Tab.6 Prototype bridge parameters

因此,对于不同的支承约束系统设计,由IM条件下的易损性函数推导的桥梁抗震性能指标是无法找到统一形式的,不利于支承约束系统的设计与优化。采用EDP代替地震动IM,建立的易损性曲线如图8所示。

图8 EDP条件下严重损伤状态的构件级易损性曲线Fig.8 Component-level fragility curves of severe damage state conditioned on EDP

由图8可见,在EDP条件下,三种设计工况的桥墩和支座严重损伤状态的易损性曲线发生重合,表明桥墩和支座的损伤概率将为对不同的支承约束系统设计不敏感,即无论支承约束系统如何设计,只要构件的EDP超过某一阈值时,构件将产生一致概率的损伤。这是因为对于特定桥梁,大量的地震动是主要的不确定性源,不同IM水平下计算的构件EDP的概率分布函数产生了一致的方差。所以,EDP条件下的易损性能够跨越不同的支承约束系统设计,进而可推导出统一形式的性能指标。

扩展到桥梁群组,概率地震分析的不确定性源进一步纳入了结构、几何和材料等特性,图9分别显示了logistic回归建立的各损伤状态下以EDP为条件的桥墩和支座的构件级易损性曲线。分析由式(1)回归的结果发现,除了桥墩LS-3状态的易损性曲线受墩高的影响显著外,其他易损性曲线受桥梁属性的影响很小,各桥梁的易损性曲线甚至与均值易损性曲线相重合。需要注意的是,不同墩高的桥墩当发生相同的EDP时,对应的倒塌概率将不同,这主要是因为不同墩高的倒塌能力阈值差异大引起的,例如,高墩易产生较大的位移延性导致倒塌概率比矮墩要高。

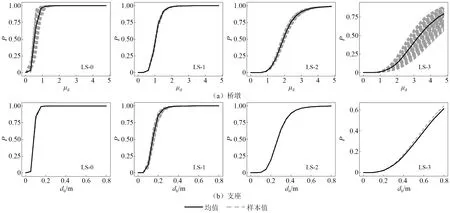
图9 EDP条件下桥梁群组的构件级易损性曲线Fig.9 Component-level fragility curves of the bridge portfolios conditioned on EDP

3.2 抗震性能优化目标函数

根据logistic回归建立的以EDP为条件的易损性推导桥梁系统级RCR,考虑到桥墩和支座的重建(更换)成本不同,ccol∶cbea取0.75∶0.25。由式(2)计算各桥梁的系统级RCR,图10显示了11 m墩高下RCR与EDP之间的关系。由图10可见,系统级性能指标RCR随着EDP的发展形成单调增加的曲面,其范围约为 0～0.8,回归残差小于3%。为了便于设计实践,可通过等高线投影做出RCR相对于μd和db的设计等高线。RCR的设计等高线在μd方向上具有变大的梯度,而在db方向上梯度的几乎不发生变化,这反映了RCR受桥墩响应影响较大。可见,以EDP为条件推导的RCR是均匀的函数曲面,可以用作支承约束系统优化设计的性能目标函数。

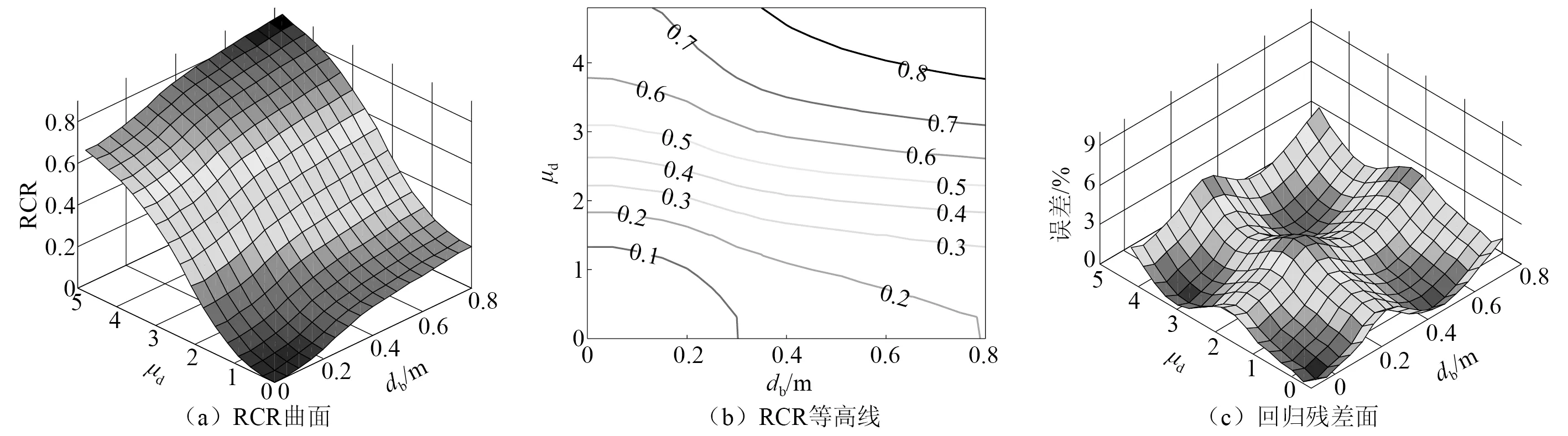
图10 11 m墩高的桥梁系统级性能指标RCRFig.10 Uniform system-level performance index RCR for the bridge with 11 m pier height

构成RCR性能指标的基本组成是桥墩和支座以EDP为条件的易损性,因此,使用式(6)将RCR与μd和db的关系回归为闭合公式

(6)

式中,系数b,λ和β可以通过最小化回归估计值和计算数据之间的误差平方和确定,即

(7)

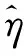
采用式(6)拟合的不同墩高下桥梁性能指标RCR,其均方误差(mean squared error,MSE)不超过0.05,说明拟合的RCR闭合公式具有较高的预测能力,能够反映RCR与各EDP的关系。拟合结果显示μd项的系数受墩高变化影响显著,db项的系数受墩高影响不明显,可按式(8)取值

b1=0.059 4ln(Ha)+0.498 6,R2=0.94,
λ1=-0.034 2ln(Ha)+3.472,R2=0.98,
β1=-0.028 3ln(Ha)+1.930 1,R2=0.99,
b2=0.183,λ2=0.320,β2=0.159

(8)

至此,为汶马路简支梁桥群组的抗震性能指标提供了统一形式,可作为优化程序的目标函数。实质上,RCR为μd和db分配了非线性权重,综合考虑了地震作用对桥墩和支座的影响,将多目标优化过程转换为单目标优化过程,简化了优化程序,统一形式的目标函数将提高优化效率。

3.3 桥梁支承约束系统优化设计

在抗震设防水准下,由式(6)和式(8)建立的RCR作为优化目标函数,通过图1的程序确定线路中桥梁横向支承约束系统的最优设计参数,以表6桥梁为例说明。选取地震动组件中的7条强地震动,作为指定抗震设防水准下桥梁结构的输入地震动,具体信息如表7所示。考虑到该线路场地,50年超越概率10%对应的地震动峰值加速度约为0.18g(E1地震作用),选取的7条强地震动的均值谱与50年内超越概率5%的规范谱相匹配。为了实现多水准设防下优化桥梁结构的性能,将7条选定的地震动PGA缩放到4个不同的水准,即0.2g,0.3g,0.4g和0.5g。在每个水准下,优化过程基于7条地震动计算的桥墩位移延性系数均值和支座位移均值产生最佳的支承约束系统设计。

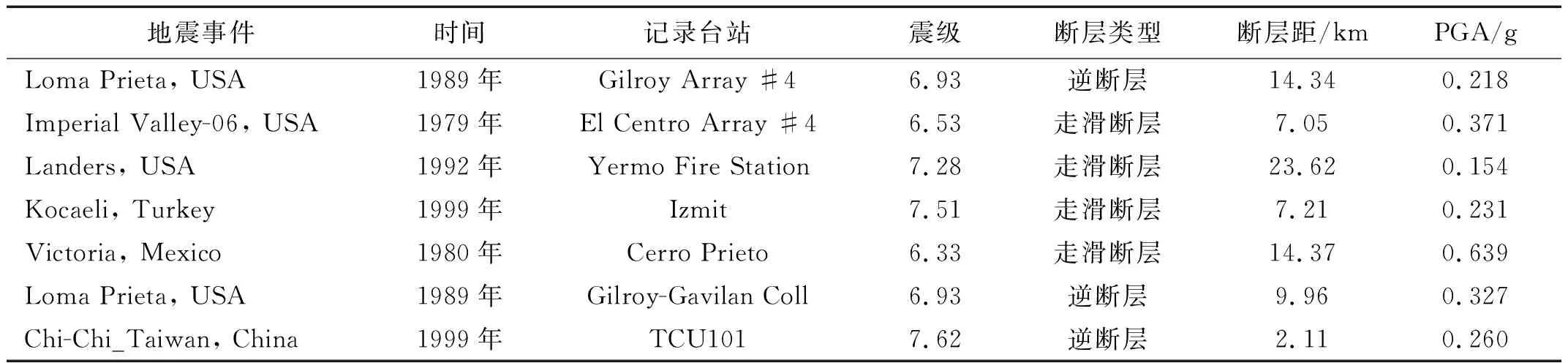
表7 7条地震动记录信息Tab.7 Information for 7 ground motion records

图11展示了在考虑的各设防水准下案例桥梁支承约束系统的遗传优化过程,每个图给出了每一代的最佳适应值和平均适应值。由图11可见:在0.2g的水准设防下,遗传优化在RCR约为4.0%时开始,并在22代后收敛到1.7%的最小RCR;在0.3g的水准设防下,遗传优化在RCR约为7%时开始,并在18代后收敛到2.66%的最小RCR;在0.4g的水准设防下,遗传优化在RCR约为9%时开始,并在33代后收敛到3.44%;在0.5g的水准设防下,遗传优化在RCR约为15%时开始,并在25代后收敛到4.48%。发现在不超过0.5g的设防水平下,采用铅芯橡胶支座的支承约束系统,最佳RCR一般处于2.2%～4.5%。

图11 案例桥梁在各抗震设防水准下的遗传优化结果Fig.11 Genetic optimization results of the prototype bridge under various seismic fortification levels

表8列出了在0.2g,0.3g,0.4g和0.5g设防水准下案例桥梁最优的支承约束系统设计参数。由于每级设防水准都会获得一组优化设计参数,但是为了解决与不同桥址处的各种地震危险性水平下的设计参数差异,本文采用每组设计参数的平均值为该桥梁建议的支承约束系统设计。将平均值Qb≈0.172QC,K2,b≈0.057K1,C作为该桥梁支座的屈服强度和屈服后刚度,其值分别为345 kN和3 930 kN/m。挡块与主梁的间隙取为0.102 m,挡块刚度取为134.4×104kN/m。

表8 案例桥梁的横向支承约束系统参数优化结果Tab.8 Parameter optimization results of bearing restraint system for the prototype bridge

对应不同墩高的桥梁,在各设防水准下对各桥梁实施优化程序,图12展示了各桥梁支承约束系统参数的优化结果。由不同墩高下的参数箱线图发现,各墩高对应的铅芯橡胶支座屈服强度Qb均值处于(0.16±0.02)·QC,屈服后刚度K2,b均值处于(0.054 8±0.008 1)·K1,C,挡块间距Gapsk均值处于(0.098±0.012)m,各桥梁的挡块弹性刚度Ksk的优化结果离散性较大,刚度均值为185×104kN/m,表现出Gapsk取值较大,Ksk取值相对较小的规律。由此可以说明,采用铅芯橡胶支座的支承约束系统中支座的屈服强度Qb、屈服后刚度K2,b以及挡块间距Gapsk的设计取值是关键。

图12 各桥梁支承约束系统参数优化结果Fig.12 Parameter optimization results of the bridge bearing restraint systems

3.4 优化桥梁的抗震性能验证

为了验证所选择支承约束系统设计的有效性,优化设计与两种初始设计方案进行对比。初始设计1为弱隔震设计,即Qb/QC=0.9,K2,b/K1,C=0.09,Gapsk=0.05 m,Ksk=400×104kN/m;初始设计2为强隔震设计,即Qb/QC=0.1,K2,b/K1,C=0.01,Gapsk=0.15 m,Ksk=30×104kN/m;优化设计中,Qb和K2,b取各墩高的桥梁在各级设防水准下优化的平均值,Gapsk和Ksk取为0.098 m和185×104kN/m。图13显示了0.3g和 0.4g地震动设防水准下各桥梁不同设计下的RCR对比。可见,优化设计显著降低了该桥梁E2地震作用(PGA为0.31g)及大于E2地震作用下的RCR。在 0.3g时,优化设计的RCR相对于初始设计1和初始设计2的最高下降值分别可达77%和64%,各桥梁的RCR均在3.2%以下;在0.4g时,优化设计的RCR相对于初始设计1和初始设计2的最高下降值分别可达75%和70%,各桥梁的RCR均在4.2%以下。

图13 0.3g和0.4g设防水准下各桥梁不同设计的RCR对比Fig.13 Comparison of RCRs of the different designs for the bridge portfolios at PGA=0.3g and PGA=0.4g

4 结 论

本文采用桥梁统一系统级指标RCR和遗传算法建立地震作用下基于性能的中小跨径桥梁支承约束系统优化程序。其中,考虑了地震动以及桥梁结构、几何与材料等的非确定性,推导了适用于桥梁群组的统一性能指标桥梁系统级RCR,将其作为优化程序的目标函数。对汶马路中简支梁桥群组进行了应用研究,采用铅芯橡胶支座,通过该程序优化桥梁群组的横桥向抗震性能,得到以下结论:

(1) 以EDP为条件,采用logistic回归建立桥梁群组的构件级易损性函数,回归结果表明,桥墩和支座的损伤概率对不同的支承系统设计不敏感。

(2) 由EDP条件下的构件级易损性函数、损伤率和修复成本关系推导出地震作用下桥梁群组的系统级RCR曲面,该曲面随桥墩高度的变化发生改变,在桥墩位移延性方向上具有较大梯度,在支座位移方向上梯度较小。即使进行新的支承约束系统参数设计,RCR曲面仍然不变,可以作为优化设计的目标函数。

(3) 对该桥梁群组的抗震性能优化表明,支座屈服强度约为(0.16±0.02)倍的桥墩屈服强度且屈服后刚度约为(0.054 8±0.008 4)倍的桥墩弹性刚度,挡块与主梁的间隙约为0.098 m,挡块刚度约为185×104kN/m时,桥梁将具有最佳的抗震性能。

(4) 检验优化程序的可行性和有效性表明基于性能的支承约束系统设计优化能够降低因地震所产生的损失,在0.3g和0.4g设防水准下,优化设计的RCR相比于初始设计下降可达64%～77%,分别降至3.2%和4.2%。