振幅放大型钢轨吸振器对弹性波传播的控制研究

冯青松, 张瀚文, 郭文杰, 梁玉雄, 陆建飞

(1. 华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室,南昌 330013;2. 江苏大学 土木工程与力学学院,江苏 镇江 212013)

近些年我国轮轨交通发展迅速,在给居民的出行带来巨大便利的同时,也引发了新的噪声污染问题。从噪声的声源来看,轮轨噪声占主导地位,而钢轨振动又是轮轨噪声最主要的贡献源[1-2],因此对钢轨采取相应的减振措施可以使轮轨噪声得到有效的控制。

针对钢轨的减振降噪措施有很多种,包括钢轨的重型化和无缝化、阻尼钢轨[3]以及安装动力吸振器等。其中,钢轨动力吸振器具有减振效果好、易于安装及维护等特点,尤其对于已经建成的线路,安装动力吸振器无疑是实现减振降噪的最优措施之一,其作用原理是给钢轨结构附加上质量-弹簧-阻尼系统,使钢轨同质量块之间产生谐振及阻尼耗散从而降低钢轨的振动。

国内外已有不少关于动力吸振器应用于轨道结构减振降噪的研究。Wu[4]分析了吸振器的不同参数和安装位置对钢轨减振效果的影响。Thompson[5]提出了一个多自由度多调谐频率的组合式吸振器,可以在更宽频范围内实现减振降噪。孙晓静等[6]对安装了动力吸振器的钢轨的垂向振动进行了现场测试,发现动力吸振器能在特定频段有效抑制钢轨振动。孟铎[7]建立了按周期规律附加吸振器的轨道结构模型,并分析了吸振器参数对钢轨振动带隙的影响。Wang等[8]同样基于带隙机理研究了周期性布置吸振器对钢轨振动的衰减效果,发现新引入的局域共振带隙和原来的轨道结构带隙之间存在耦合和跃迁,并在耦合位置形成宽频带隙,从而抑制结构中弹性波的传播。

目前,关于钢轨动力吸振器的研究及优化设计基本都是围绕如何在更宽的频率范围内实现减振降噪开展的,要想拓宽吸振器的减振频率段必须增大吸振器的质量,而自身过大的质量难免会给吸振器的实际工程应用造成困难。因此,本文从控制周期结构中弹性波传播的角度出发,基于振幅放大机制提出了一种新型的钢轨动力吸振器,并对其减振效果进行了对比分析,为在不增大吸振器质量的前提下提升其工作性能提供了参考。

1 吸振器的设计

本文设计的基于振幅放大机制的钢轨动力吸振器,如图1所示,将其布置在钢轨的跨中位置[9]。吸振器整体类似于一个杠杆装置,一头为连接钢轨底部的磁座;另一头为可以叠加橡胶垫层和铅块的承重台;支座和下部的轨道板相连接。在实际工程中,通过改变承重台上铅块的数量和换用不同规格的橡胶垫层来调节吸振器系统的质量和刚度等参数,从而改变吸振器的设计频率,满足不同频率段的减振需求。

图1 基于振幅放大机制的钢轨吸振器(mm)Fig.1 Schematic diagrams of rail vibration absorber using an amplitude magnification mechanism (mm)

为便于理解新型吸振器的振幅放大特性,给出了该装置的平面简化分析示意图(见图1(b))。杠杆两端力臂长度的分配比即振幅的放大倍数表示为

σ=l1/l0

(1)

式中:l0为刚性杆左端点到支座顶端的水平距离;l1为刚性杆右端点到支座顶端的水平距离。

此外,图1(b)中的铰支支座与轨道板之间为刚性连接,刚性杆与轨底、刚性杆与铰支支座之间均为铰接连接,其中刚性杆可以沿着支座顶部的铰接点水平方向滑移,以确保该机构不会发生部件卡壳从而导致失效。

当振幅放大倍数σ取值为3时,吸振器的整体尺寸见图1(c),虽然相较于常规的轨底吸振器,振幅放大型吸振器的尺寸大小基本不会受到轨底可利用空间的制约,但杠杆长度分配比和铅块质量的选取等仍可能受制于轨道板上的可利用空间及杠杆的极限承载能力,所以相应的振幅放大倍数σ和质量m等参数的取值也不宜过大。

2 计算模型

本文基于能量法计算周期性布置吸振器的钢轨结构的带隙,由于主要考虑吸振器对钢轨振动的衰减效果,且轨道板等下部基础的刚度较大,近似于刚性基础,为便于分析和计算,将轨道结构简化为如图2所示的周期性布置吸振器系统的单层梁模型,采用Timoshenko梁模拟钢轨,弹簧模拟扣件,取一个长度为l的典型单元进行分析,由于运动车辆引起的周期性钢轨结构振动以垂直方向的振动为主,故本文选择钢轨结构的垂向振动作为研究对象。

图2 周期性布置振幅放大型吸振器的钢轨示意图Fig.2 Schematic diagrams of rail with periodic arrangement of amplitude magnification vibration absorber

钢轨的位移场表示为[10]

(2)

式中:w(x,t)为钢轨振动的垂向位移;θ(x,t)为钢轨的截面转角;φi(x)为基函数;ai(t)和bi(t)为权重系数。

由于本文提出的新型吸振器通过杠杆机构放大了钢轨跨中点的振幅,所以连接质量块的弹簧变形量为[σ·w(0)-u*](u*为系统中质量块的垂向位移),则典型周期单元的整体结构的动能、弯曲应变能分别表示为

(3)

(4)

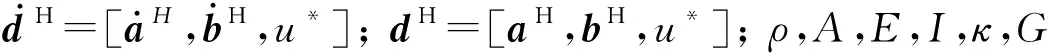
扣件的弹性势能表示为

(5)

式中,kf为扣件的垂向刚度。

在利用传统能量法进行周期结构振动带隙求解时,需要构造满足周期边界条件的位移函数[11-12],对使用者的数学构造能力要求较高,本文采用虚拟弹簧模拟周期边界条件,无需对位移函数进行构造。通过虚拟弹簧将钢轨的周期单元之间首尾连接(见图2),则典型周期单元的边界弹性势能可表示为

(6)

该典型周期单元结构自由振动状态下的拉格朗日量表示为

(7)

(8)

图3 周期性布置常规型吸振器的钢轨示意图Fig.3 Schematic diagrams of rail with periodic arrangement of conventional vibration absorber

用以表征周期性结构带隙特性的方式通常包括能带结构和传递率,通过分析有限长周期结构的传递率能够清晰地描述该结构对振动波传播的衰减能力,本文继续利用能量法对传递率进行求解。从轨道结构中选取一段由N个周期单元组成的有限长结构,在结构的左端施加一个单位垂向简谐荷载作为激振点,右端作为响应点,并提取两端点的位移幅值从而得到结构的振动传输特性曲线。

对于如图4所示的有限长钢轨结构,其动能以及考虑阻尼效应的弯曲应变能相较前述的能带计算部分只需要叠加求和即可,故不在此赘述,结构的质量矩阵M和刚度矩阵K的表达式见附录C。

图4 周期性布置振幅放大型吸振器的钢轨传递率分析示意图Fig.4 Schematic diagrams of transfer rate analysis of rail with periodic arrangement of amplitude magnification vibration absorber

对于钢轨结构的受迫振动,由于需要考虑外力做功,所以式(7)的拉格朗日量改写为

(9)

(10)

3 算例分析

本章基于能量法计算出的周期性布置两种不同的吸振器时钢轨的垂向振动带隙,并结合钢轨振动的位移导纳和振动加速度级对两种吸振器的减振效果进行对比分析,采用60 kg/m钢轨,钢轨的具体参数如表1所示。

表1 钢轨结构的基本参数Tab.1 Basic parameters of rail structure

研究表明,钢轨振动的Pinned-Pinned模态对轮轨噪声的贡献较大[13-15],本文主要针对钢轨的Pinned-Pinned频率设计动力吸振器的参数,由于算例所选用的钢轨的第一阶Pinned-Pinned共振发生在频率1 073 Hz处[16-17],因此在动力吸振器的质量-弹簧-阻尼系统中,质量m取4 kg,刚度k取1.8×108N/m,阻尼损耗因子c取0.2,振幅的放大倍数σ取3,模拟周期边界条件的人工弹簧刚度分别取ktx=1012N/m,krx=1012N/rad,位移型函数表示为

(11)

式中,n=1,2,…,R,R为截断项数。

由于在计算过程中存在叠加求和,因此计算结果的准确性受到截断项数R的影响,需要对其进行收敛性分析。以图3所示的周期性布置常规型吸振器的钢轨结构的能带求解为例。从频散曲线中挑选波数在0.5×π/l处的前三阶频率作为研究对象,计算结果如图5所示。

图5 波模态频率随截断项数R取值变化曲线Fig.5 Change curve of the wave modal frequency with the truncation term R

由图5可以看出,在0～3 500 Hz的分析频段范围内,当R取值为8时,波模态频率值已经基本收敛,因此将它作为后续算例分析中截断项数的取值。

3.1 模型验证及带隙分析

为了证明所提出模型的可靠性,基于有限元法对布置两种不同吸振器时钢轨结构的带隙计算结果进行验证。利用COMSOL Multiphysics有限元软件的固体力学模块进行建模分析,相较于其他商用有限元软件,COMSOL能够直接添加Floquet周期性边界条件。布置振幅放大型吸振器的钢轨结构的有限元模型,如图6所示。

图6 布置振幅放大型吸振器的钢轨典型单元有限元模型Fig.6 Finite element model of a typical unit of rail arranged amplitude magnification vibration absorber

钢轨及吸振器系统均采用实体单元建立,扣件简化为线弹簧基础,钢轨模型相关参数的取值与表1一致,为保证吸振器系统中用于振幅放大的杠杆具有足够大刚度,刚性杆材料的弹性模量值取1016Pa。

计算出按周期规律布置两种不同吸振器的钢轨垂向振动带隙的理论及有限元计算结果,如图7所示。

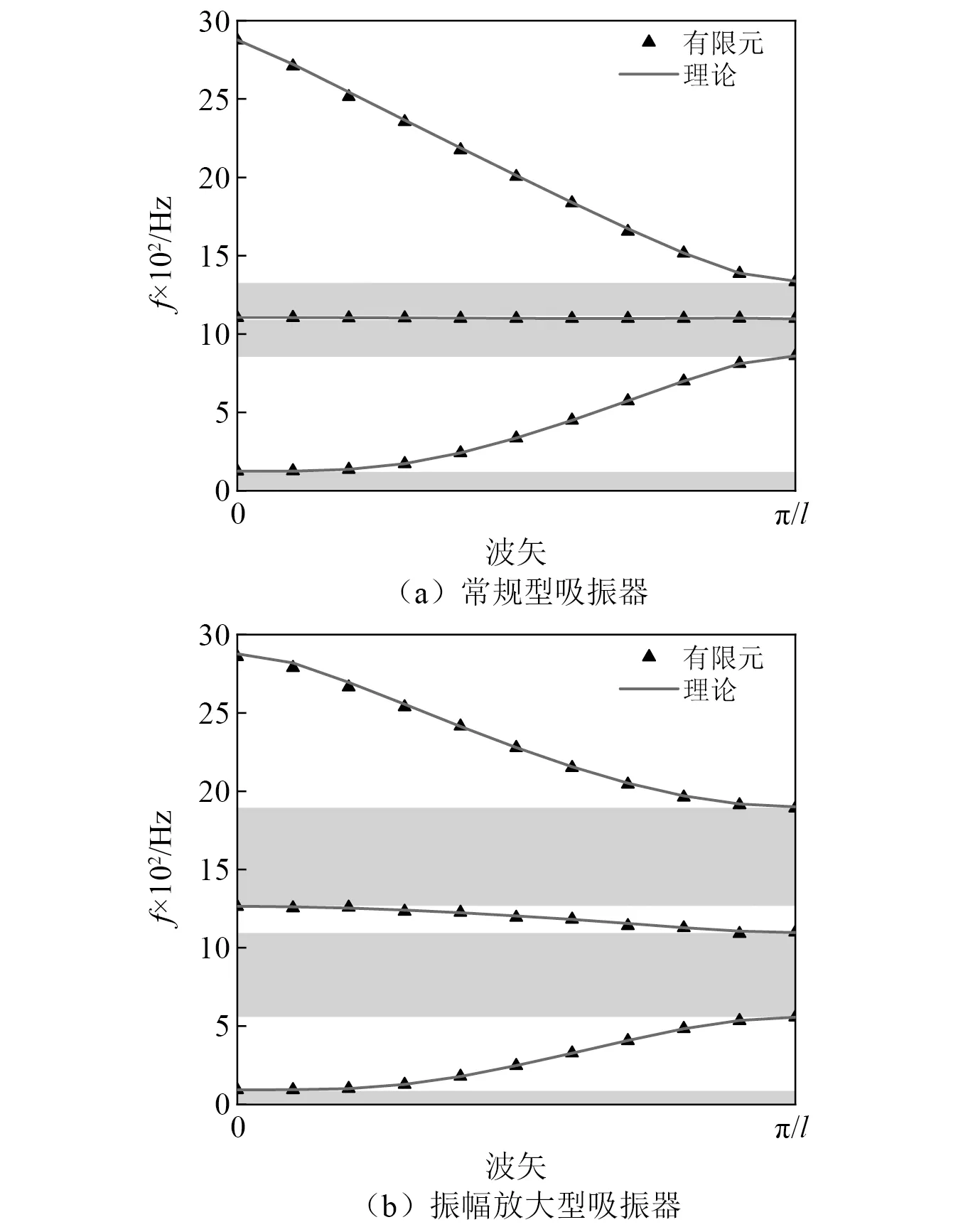
图7 布置两种不同吸振器时钢轨的频散曲线Fig.7 Frequency dissipation curve of the rail with arrangement of two different vibration absorbers

对比频散曲线的理论计算结果与有限元计算结果可以发现,两者吻合度很好,证明了本文所提计算模型的可靠性。将对应于两种吸振器的理论及有限元计算结果进行对比分析,如表2所示。

表2 周期性布置两种吸振器时钢轨的振动带隙频率对比Tab.2 Comparison of the vibration band gap of the rail with periodic arrangement of two different vibration absorbers 单位:Hz

从图7和表2中可以看出,在吸振器的其他参数一致的情况下,相较于常规吸振器,振幅放大型吸振器能够显著拓宽第二阶带隙(即局域共振带隙)和第三阶带隙(即Bragg带隙),并在Pinned-Pinned振动频率附近有效地拓宽了带隙范围,因此,本文提出的振幅放大型吸振器可以在更宽的频率范围内抑制钢轨结构中振动的传播。同时,由于振幅放大机制通过放大质量块的等效质量,相应地增大了整个钢轨系统的等效质量,所以图7(b)中的第一阶带隙的截止频率有小幅度降低。

进一步利用能量法分析振幅放大机制对振动传递率的影响,为了在有限周期情况下更加准确地表征吸振器的振动衰减效果,选取120 m长的钢轨进行分析,提取距离激振点10跨处位置的响应,计算得到按周期规律布置两种不同吸振器时钢轨结构的振动传输特性曲线结果,如图8所示。

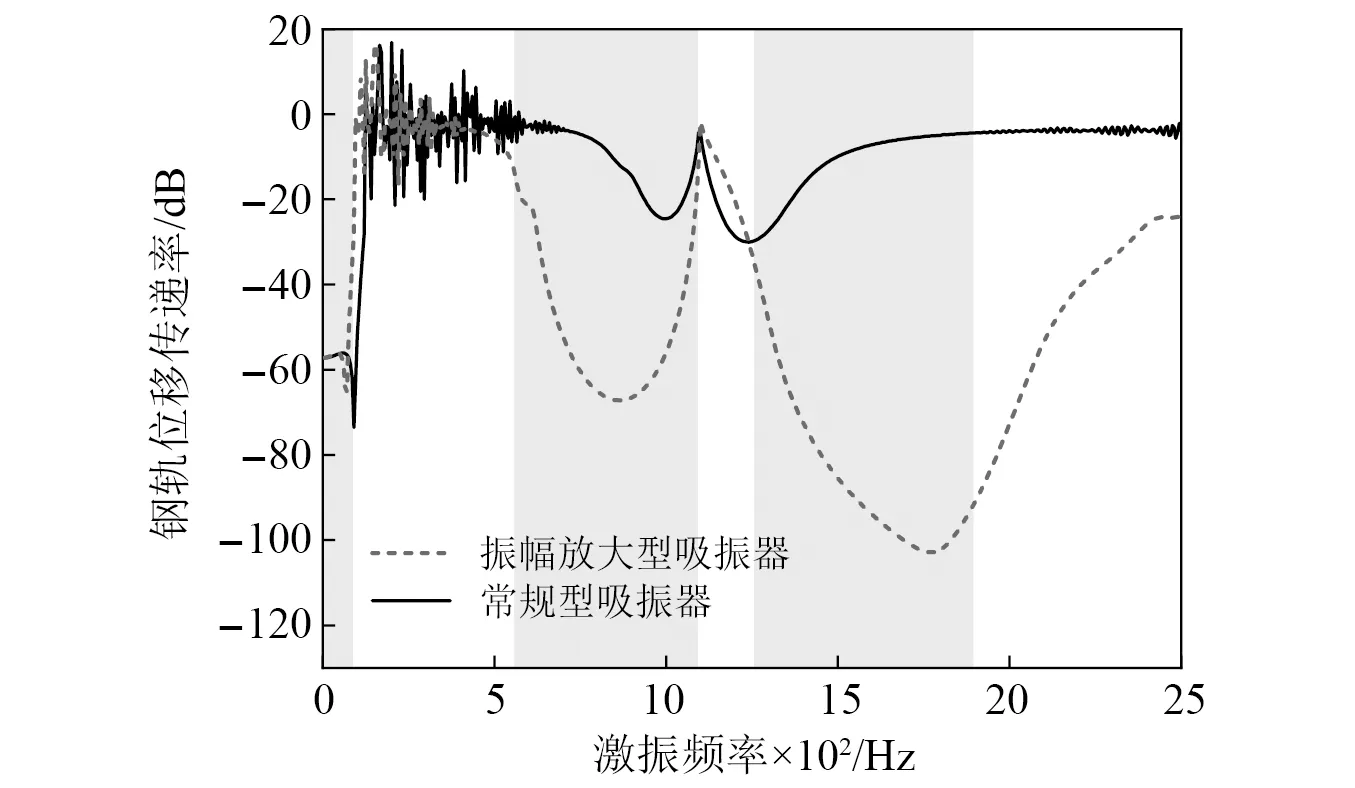
图8 布置两种不同吸振器时钢轨的振动传输特性曲线Fig.8 Characteristic curves of vibration transmission in the rail with arrangement of two different vibration absorbers

从图8可以看出,在吸振器相关参数一致的情况下,相较于常规吸振器,振幅放大型吸振器不仅能明显地拓宽振动衰减范围,还能有效地提高衰减量,如图8所示,以引入吸振器后新产生的局域共振带隙(即第二阶带隙)为例,常规吸振器的最大衰减量为24.5 dB,振幅放大型吸振器的最大衰减量则达到了67.2 dB。且对比3.1节中周期性布置振幅放大型吸振器钢轨的禁带范围的计算结果,传输特性曲线中的振动衰减域范围明显得到了拓宽,这是由于振幅放大机制有效地增大了阻尼耗散,而阻尼对带隙的影响主要表现在它能有效拓宽传输特性曲线中的弹性波衰减域的范围[18-19]。因此,振幅放大型吸振器不仅显著拓宽了钢轨中弹性波传播的衰减域,还增强了域内的衰减效果。

3.2 位移导纳及振动加速度级分析

比较布置两种不同吸振器时钢轨振动的位移导纳和振动加速度级的结果,以分析不同吸振器的减振效果,为使结果更加精确,钢轨的长度取300 m,在中间单元的跨中位置处施加一个垂向的单位简谐荷载,计算得到未布置吸振器和布置两种不同吸振器时激振点处的位移导纳曲线和1/3倍频程振动加速度级频谱曲线,分别如图9(a)、图9(b)所示。同时,为了进一步反映轮轨激振处附近的振动衰减情况,在钢轨上以激振点为中心往线路两端方向每隔0.6 m选取一个测点,共选取9个测点的均方根振级来对激振点附近一定范围内的振动衰减效果进行综合评价,计算得到未布置吸振器和布置两种不同吸振器时钢轨测点处的均方根振级曲线,如图9(c)所示。

图9 钢轨的位移导纳和振动加速度级Fig.9 Displacement admittance and vibration acceleration stage of the rail

从图9(a)可以看出,未布置吸振器时钢轨在一阶Pinned-Pinned振动频率附近的垂向振动导纳峰值为1.24×10-9m/N,而两种吸振器均能在设计的频率处有效地降低钢轨振动的位移,其中安装常规型吸振器后位移导纳降低为0.39×10-9m/N,而安装振幅放大型吸振器后则降低为0.26×10-9m/N,同时,在设计的减振频率附近,有效减振频率范围也由常规型吸振器的935～1 335 Hz拓宽为860～1 425 Hz(见图9(a)中的阴影部分);从图9(b)和图9(c)可以看出,相较于未布置吸振器时的情形,常规型吸振器使钢轨振级降低了2.8 dB,均方根振级降低了6.4 dB,而振幅放大型吸振器则使钢轨振级降低了8.5 dB,均方根振级降低了14.3 dB,吸振器的有效减振频率范围也从873～1 453 Hz和809～1 483 Hz分别扩大至816～1 516 Hz(见图9(b)中的阴影部分)和630～1 571 Hz(见图9(c)中的阴影部分)。综上分析可知,本文提出的振幅放大型钢轨吸振器减振效果要明显优于常规型吸振器。

4 参数分析

4.1 振幅放大机理分析

振幅放大机制能够提升动力吸振器减振性能的根本原因在于有效地增大了吸振器的等效质量、刚度和阻尼。对于图3所示的常规型吸振器,其动能以及考虑阻尼效应的弹簧应变能分别表示为

(12)

式中,u为振子的垂向位移。而对于图1(b)所示的振幅放大型吸振器,由于利用杠杆机构对钢轨跨中的振幅进行了放大,杠杆另一端与弹簧的连接点处以及质量块的垂向位移分别变更为σ·w(0)和σ·u。此时,振子的动能以及考虑阻尼效应的弹簧应变能分别表示为

(13)

图10 振幅放大机理分析对比图Fig.10 Comparison diagram of amplitude magnification mechanism analysis

从图10可以看出,保持吸振器参数不变,调节振幅放大倍数为3与按照9倍同比例增大系统的质量、刚度和阻尼相比,两者对应的频散曲线以及振动传输特性曲线完全一致,证明了振幅每放大σ倍,系统的质量、刚度和阻尼都同步增大σ2倍,进而将吸振器的减振性能提升了σ2倍。

4.2 振幅放大倍数对减振效果的影响分析

通过机理分析可以发现,振幅放大的倍数会影响吸振器的减振效果,进一步分析不同振幅放大倍数对减振效果的影响。吸振器系统中质量块的质量m取4 kg,刚度k取1.8×108N/m,阻尼损耗因子c取0.2,比较布置常规型吸振器和放大倍数σ分别取2,3,4,5的振幅放大型吸振器时,钢轨的振动传递率、激振点处位移导纳、激振点处1/3倍频程振动加速度级和激振点附近1/3倍频程均方根振动加速度级,计算结果如图11所示。

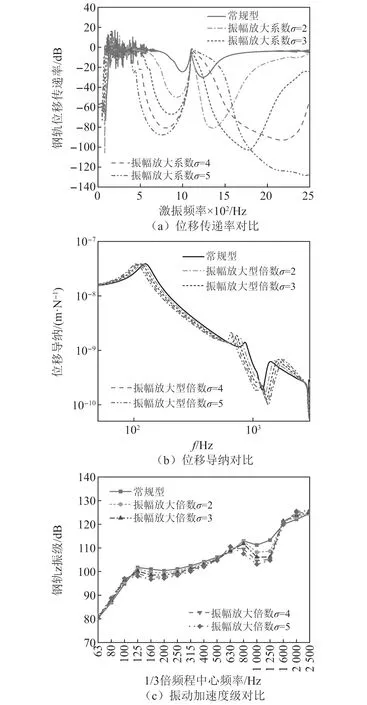
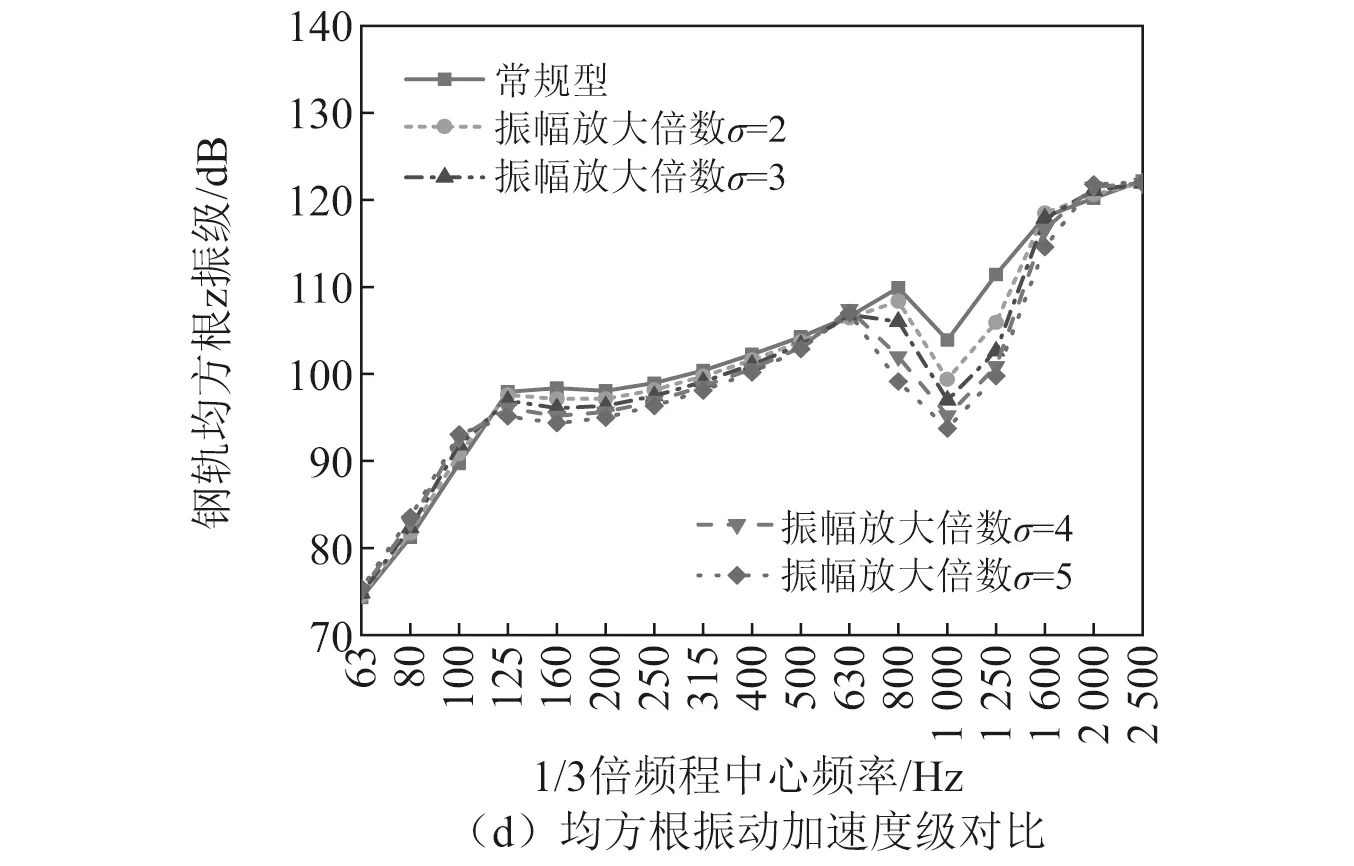
图11 振幅放大倍数对振动传输衰减能力的影响Fig.11 Effect of amplitude magnification times on the ability of vibration transmission attenuation

从图11可以看出,随着振幅放大倍数的增加,相应的减振频率范围呈现不断扩宽的趋势,振动的衰减效果也不断增强。因此,可以通过增加振幅放大型吸振器的振幅放大倍数提升其减振性能,但由于过大的倍数可能导致杠杆的设计长度过度增加,从而占用更多轨道上的空间,因此,应根据实际情况设置合理的振幅放大倍数。

5 结 论

本文提出了一种基于振幅放大机制的钢轨动力吸振器,以周期性布置振幅放大型吸振器的钢轨为例,利用能量法对其带隙进行了计算和分析,建立有限元模型来验证其能带结构,并从位移导纳和振动加速度级的角度分析其减振效果,得出以下结论:

(1) 当相关参数一致时,振幅放大型吸振器与常规型吸振器相比拥有更加优良的减振性能,这是由于吸振器的等效质量、刚度和阻尼都同比得到了放大。

(2) 振幅放大型吸振器对钢轨减振频率段的拓宽效应表现在其能明显地增大第二、第三阶带隙的宽度,对第一阶带隙影响不大。

(3) 由于同比增加了阻尼损耗,振幅放大型吸振器不仅拓宽了带隙的范围,还增强了振动波在带隙内的衰减效果。

(4) 可以适当地通过增加放大倍数来稳定提升振幅放大型吸振器的减振性能,但如果杠杆过长可能会侵占线路上的空间,所以应根据实际工程中的情况合理调整振幅放大倍数。

附录A

1. 质量矩阵

2. 刚度矩阵

附录B

替换后的刚度矩阵

附录C

1. 叠加求和后的质量矩阵

2. 叠加求和后的刚度矩阵

式中:xn(n=1,2,…,N)为接入振子的位置点;O1为n×1的零矩阵;O2为1×n的零矩阵。

附录D

替换后的刚度矩阵

式中:xn(n=1,2,…,N)为接入振子的位置点;O1为n×1的零矩阵;O2为1×n的零矩阵。