框架薄壁类结构压电分流阻尼多模态减振试验研究

刘亚宁, 周嘉明, 董龙雷, 刘 建, 赵建平

(西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室,西安 710049)

近年来,压电分流阻尼技术在结构减振降噪领域得到了广泛的关注[1-2]。压电分流阻尼技术是一种以压电材料正压电效应为原理的被动控制技术,与主动控制相比,压电分流阻尼技术方法简单,易于实现,不需要大量附加的电子设备,且一般不存在控制失稳的问题[3],故而国内外学者相继开展了压电分流阻尼技术方面的研究。

Forward[4]首先提出了利用压电分流阻尼电路进行振动控制,作者仅在电路中设置电感便可对金属棒结构单模态响应进行控制。Hagood等[5]对压电分流阻尼电路中电阻和电感参数进行了定量分析,确定了一种基于传递函数的参数计算方法,用于电阻和电感最优值的确定。柳维玮等[6-8]给出了一种极点配置方法,该方法同样能够对压电分流电路参数进行准确计算。古渊等[9]的试验研究表明采用多个压电片共同控制单一模态时减振效果会有所增强。Hollkamp[10]将单模态压电分流阻尼电路进行扩展,首次将多模态电路应用到悬臂梁上实现了多个模态响应的控制。Wu[11-12]提出了一种阻塞电路可以实现三个模态同时减振。研究结果表明压电片位置与模态振型位置耦合时,振动响应显著降低,针对该问题文献[13-17]开展了基于布局优化的压电分流阻尼减振试验研究,探究了压电片位置变化时压电分流电路在悬臂梁中的振动控制效果,给出了压电分流阻尼系统中的压电片形状与布局优化规则。纯被动压电分流阻尼电路减振控制存在电路利用率低、控制频带较窄等问题,目前半主动控制压电分流阻尼电路是解决这一问题的一个有效技术手段。季宏丽等[18-21]研究了压电分流阻尼系统在悬臂梁与四边固支板中的半主动控制方法,并应用改进的合成阻抗开展了压电分流电路研究,提高了压电分流电路的控制效果。

框架薄壁类结构是飞行器中普遍存在且十分重要的结构,如航天器壁板[22]、火箭整流罩[23]以及飞机蒙皮结构[24-25]等。这类结构在实际服役环境中往往要承受严酷的噪声载荷,影响机械结构正常运作,甚至破坏结构造成安全问题。李耀光等[26-27]利用压电分流阻尼电路进行车内噪声控制,采用空腔模拟乘车室环境并在空腔外表面布置压电分流阻尼电路进行振动控制,在扬声器激励下实现了空腔内声压幅值降低。张立[28]针对飞机典型结构如飞机蒙皮、飞机加强筋、飞机壁板等结构进行压电片布局优化设计,通过行波管施加噪声载荷,取得了明显的振动控制结果。除此之外,压电分流阻尼电路在水下航行体的水动力噪声控制[29]、辐射噪声抑制[30]等方面也有应用。

目前国内将压电分流阻尼电路应用于实际工程中仍存在一定困难,系统性试验与理论对比相对较少、实际工程载荷激励下的压电分流阻尼电路减振试验不足,因此本文开展了大量试验对压电分流阻尼电路的减振效果进行研究。首先,开展了扫频激励下的单压电片单模态电路减振试验,将电路最优参数试验结果与理论计算结果进行对比分析。然后,开展了基于阻塞电路的多模态压电分流阻尼电路减振试验研究,并通过多个压电片开展了20～2 000 Hz内多个模态频率的减振试验。最后,在噪声载荷激励下开展了多模态电路减振试验,研究了20～2 000 Hz全频段振动能量和主要频率峰值的减振效果。

1 试验方案

本文选用的试验对象为四边固支铝合金板,具体尺寸如图1所示。铝合金板和夹具上加工了52个Φ6.3的通孔,实际试验操作中通过32个M6螺栓将铝合金板固定在专用试验桌上,从而达到模拟四边固支边界条件的效果。本文规定板的上面为正面、下面为反面。

图1 四边固支铝合金板尺寸图Fig.1 Dimensions drawing of aluminum alloy plate supported by four sides

压电片通过绝缘胶粘贴在铝合金板表面,布置位置如图2所示。正面压电片作为作动器使用,通过施加扫频信号来产生激励;反面压电片作为换能器使用,即将机械振动能量转化为电能进而通过电路使能量耗散。本文所有压电片均为PZT-52,其尺寸及性能参数如表1所示。铝合金板正面布置3个ICP加速度传感器用于测量结构振动响应,编号依次为#1,#2,#3,并采用加速度响应来评价减振效果。铝合金板反面布置9个压电片,编号依次为UR、UC、UL、MR、MC、ML、DR、DC、DL,根据不同的试验工况选择不同的压电片进行减振。试验现场图如图3所示。

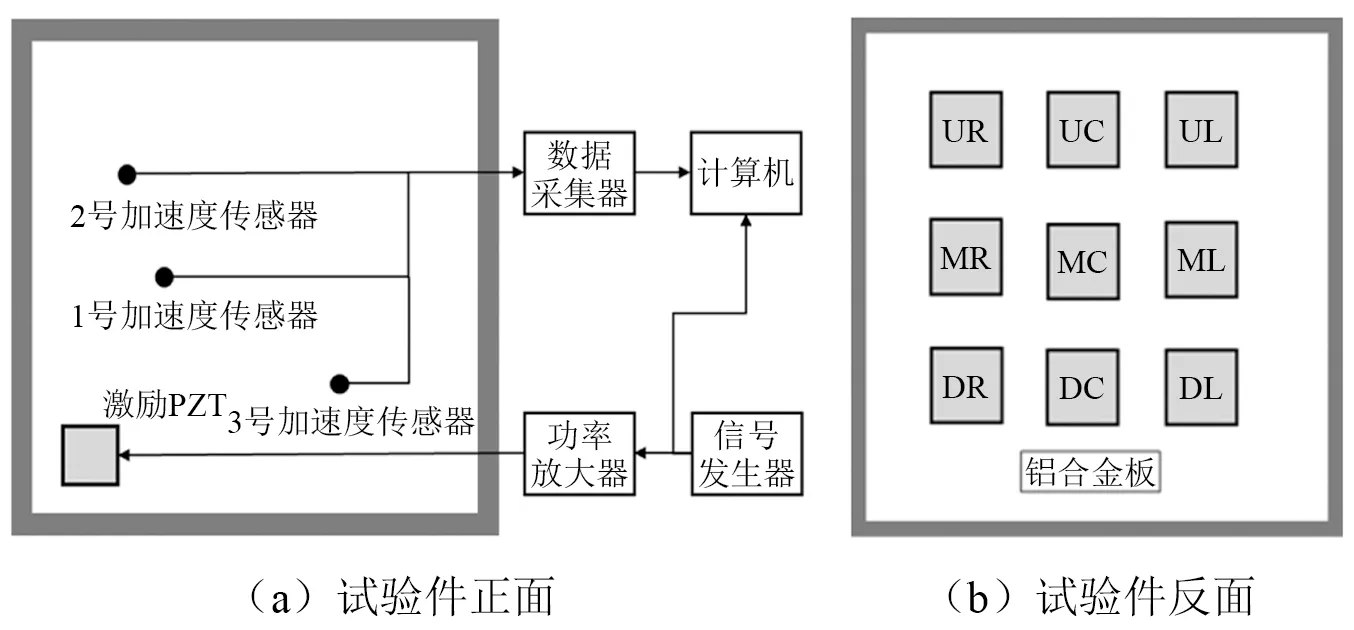
图2 试验装置示意图Fig.2 Schematic diagram of experimental device

表1 压电元件的尺寸及性能参数Tab.1 Dimensions and performance parameters of piezoelectric elements

图3 试验现场图Fig.3 The experimental device diagram

2 单压电片单模态减振试验研究

2.1 单模态电路原理

单模态压电分流电路采用RL串联电路,如图4所示。大量研究表明不同电阻值和电感值会对减振效果有影响,因而存在最优电阻值和电感值使电路的减振效果最佳。最优电阻值Ropt计算如式(1)所示

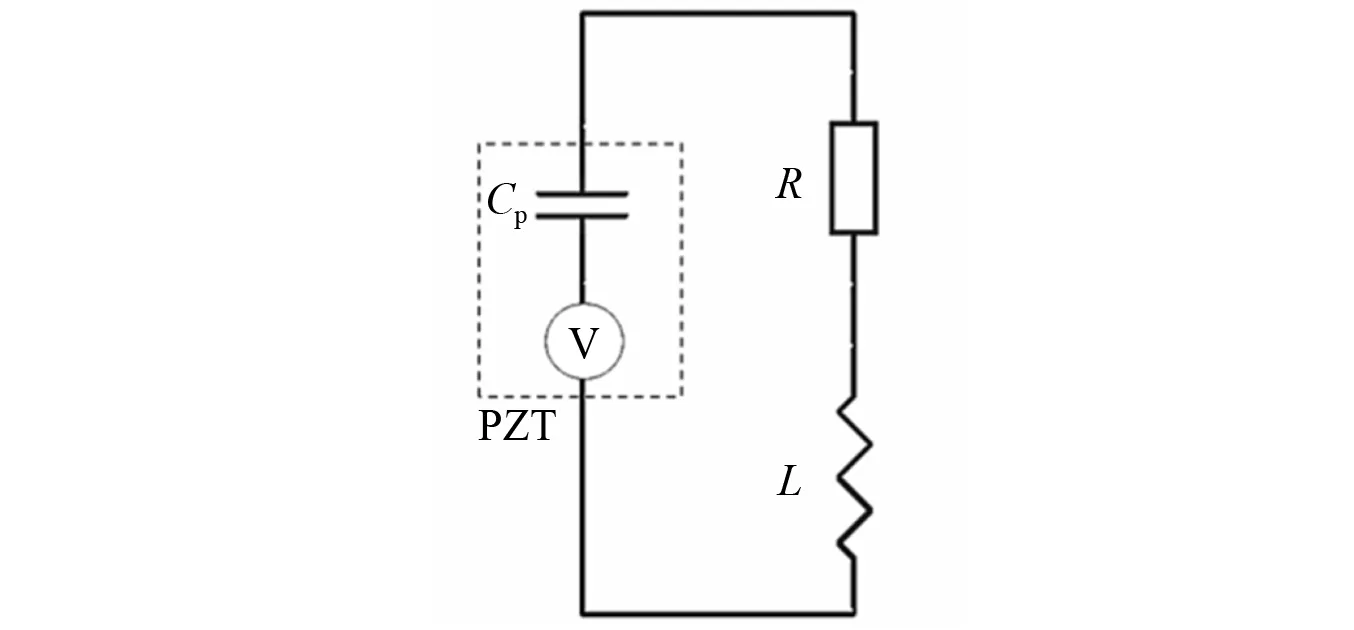
图4 RL串联电路示意图Fig.4 RL series circuit schematic diagram

(1)

式中:Kc为有效机电耦合系数;Cp为压电片的电容;ωo为分流电路开路时结构模态频率;ωs为分流电路短路时结构模态频率。

最优电感值Lopt计算如式(2)所示

(2)

2.2 电阻对减振效果的影响

分别研究不同电阻值对330 Hz和1 100 Hz两个模态频率处减振效果的影响。试验选用的换能压电片为图2(b)中的UL压电片,加速度传感器选用#1。330 Hz处在1～1 000 kΩ设置27组电阻值进行对比试验,1 100 Hz处在1～100 kΩ设置28组电阻值进行对比试验。本试验选用的电阻值制造误差均在5%以内。

在322～336 Hz内进行扫频试验,得到不同电阻值下结构动力学响应传递曲线如图5所示。对试验结果进行处理与分析,并定义曲线与坐标轴包络面积作为能量传递指标,得到图6所示的峰值/能量减振效果随电阻值变化曲线。从图中可以看出,当电阻较小或较大时均无法取得良好的减振效果,最优电阻值的试验结果在[19 kΩ, 23 kΩ]内,通过式(1)计算的理论最优电阻值为21.9 kΩ,结果表明试验结果与理论计算结果一致。

图5 330 Hz处不同电阻值下结构传递曲线图Fig.5 Structure transfer curve at 330 Hz with different resistance values

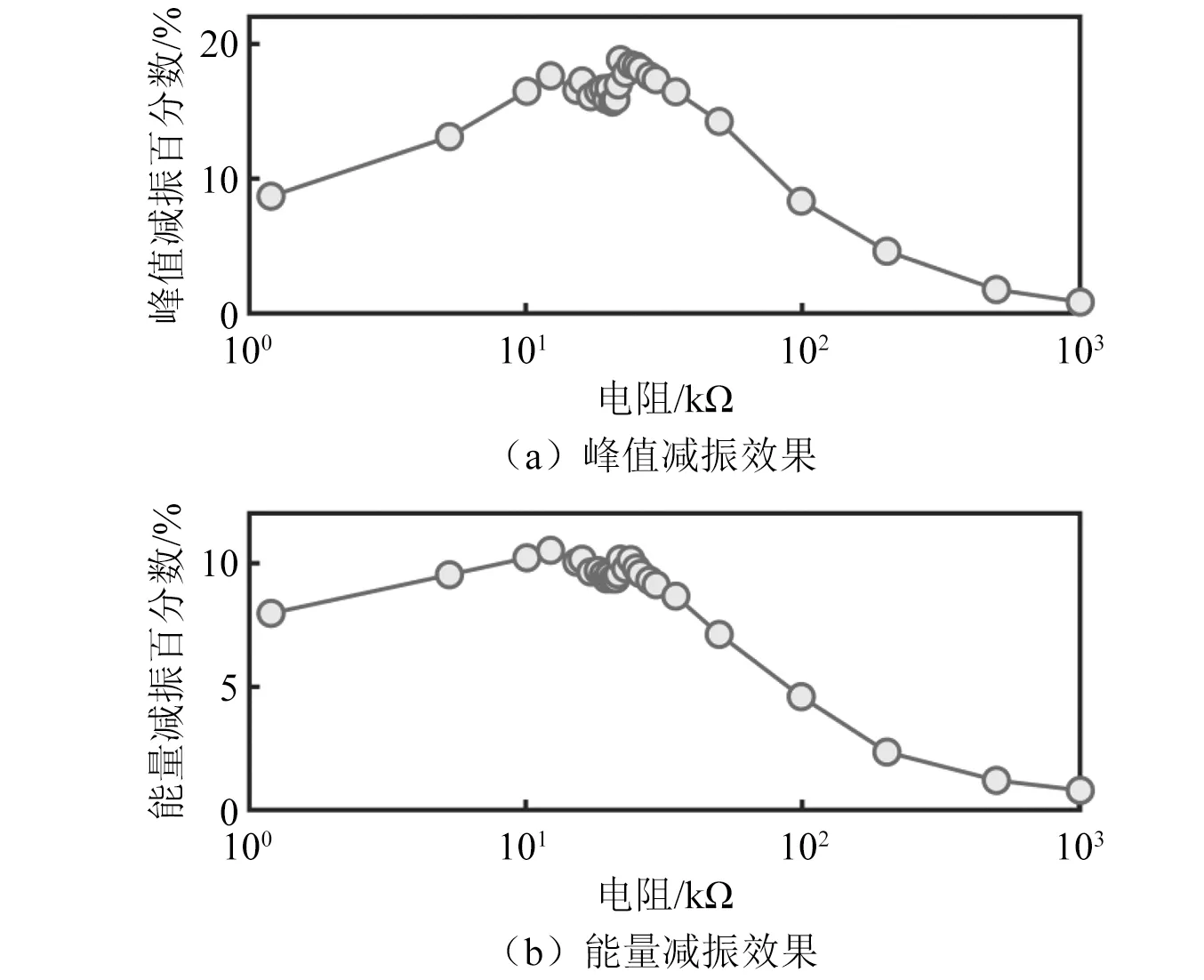
图6 330 Hz处减振效果随电阻的变化Fig.6 Diagram of vibration reduction effect changing with resistance at 330 Hz

此外,试验发现电阻值在区间[19 kΩ, 23 kΩ]内取值对减振效果的影响不明显。当电阻值为22 kΩ时,峰值和能量减振效果达到最大,分别为18.8%和10.5%。峰值和能量减振效果在该区间的波动分别为1.9%和0.9%,这就意味着电阻值的最优参数可以在一个区间内取值,具有良好的工程实用性。

在1 080～1 150 Hz内进行扫频试验,得到不同电阻值下结构动力学响应传递曲线如图7所示。对试验结果进行处理与分析,得到图8所示的峰值/能量减振效果随电阻值变化曲线。从图中可以看出,当电阻较小或较大时都无法取得良好的减振效果,最优电阻值的试验结果在[6 kΩ, 8 kΩ]内,通过式(1)计算出1 100 Hz处的理论最优电阻值为6.7 kΩ,结果表明试验结果与理论计算结果一致。此外,最优电阻值可以在[6 kΩ, 8 kΩ]中取值,与330 Hz处的结论相同。

2.3 电感对减振效果的影响

本节在最优电阻值确定的基础上,研究不同电感值对330 Hz和1 100 Hz两个模态频率处减振效果的影响。330 Hz处确定最优电阻值为21.9 kΩ,在1～30 H设置22组电感值进行对比试验;1 100 Hz处确定最优电阻值为6.7 kΩ,在0.1～2 H设置34组电感值进行试验。本试验选用的电感值制造误差在5%以内。

在322～336 Hz内进行扫频试验,得到R=21.9 kΩ时不同电感值下结构动力学响应传递曲线如图9所示。对试验结果进行处理与分析,得到图10所示的峰值/能量减振效果随电感值变化曲线。从图中可以看出,当电感较小或较大时都无法取得良好的减振效果,最优电感值的试验结果在[10 H, 11 H]内,通过式(2)计算出330 Hz处的理论最优电感值为10.1 H,结果表明试验结果与理论计算结果一致。

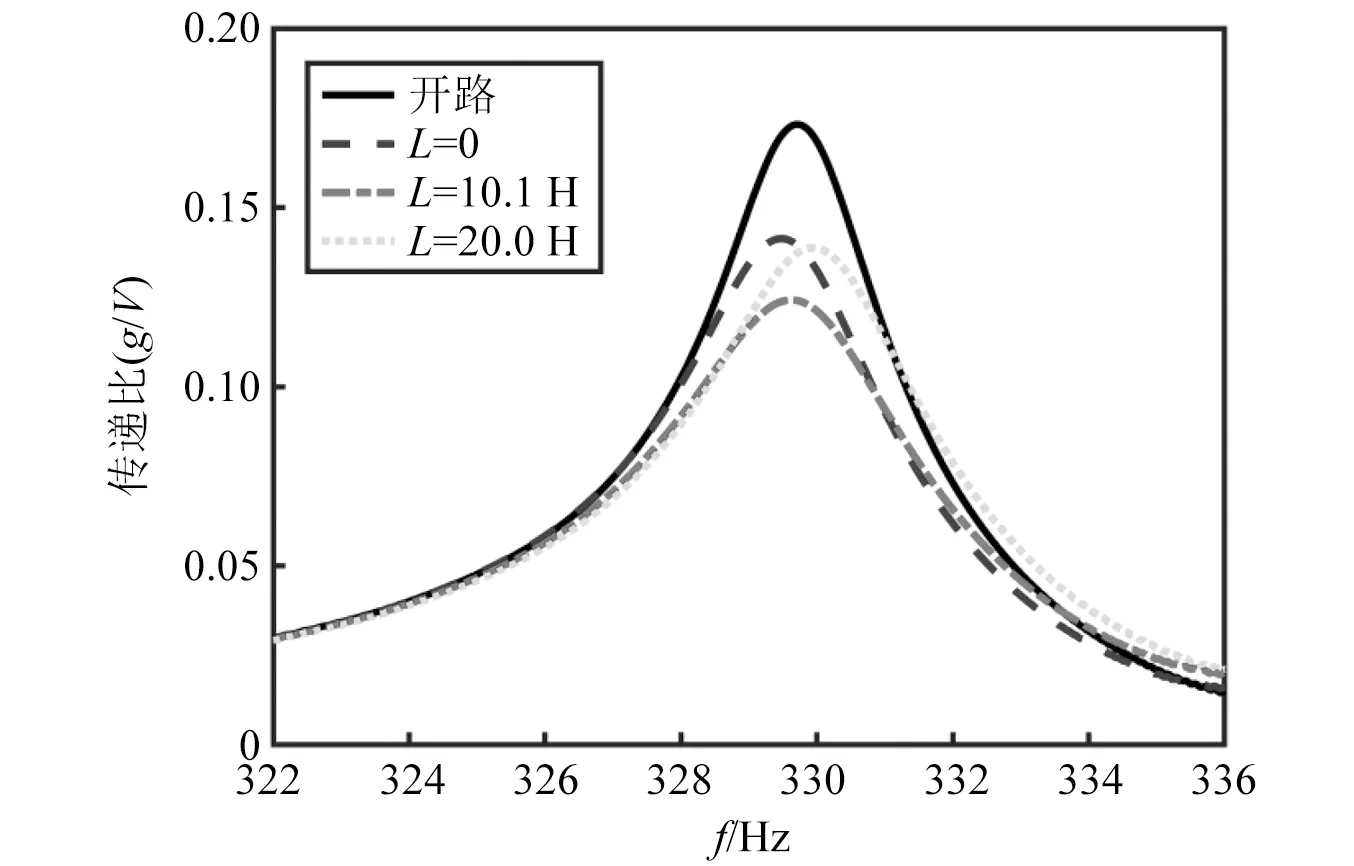
图9 330 Hz处不同电感值下结构传递曲线图Fig.9 Structure transfer curve at 330 Hz with different inductance values

图10 330 Hz处减振效果随电感变化图Fig.10 Diagram of vibration reduction effect changing with inductance at 330 Hz

此外,试验发现电感值在区间[10 H, 11 H]内取值对减振效果的影响不明显。当电感值为10 H时,峰值和能量减振效果分别为28.3%和12.5%,这两者在该区间的波动分别为0.1%和0.5%。这就意味着电感值的最优参数也可以在一个区间内取值,同样具有良好的工程实用性。

在1 080～1 150 Hz内进行扫频试验,得到R=6.7 kΩ时不同电感值下结构传递曲线如图11所示。对试验结果进行处理与分析,得到图12所示的峰值/能量减振效果随电感值变化曲线。从图中可以看出,当电感较小或较大时都无法取得良好的减振效果,最优电感值的试验结果在[0.90 H, 1.05 H]内,通过式(2)计算出1 100 Hz处的理论最优电感值为0.95 H,结果表明试验结果与理论计算结果一致。此外,最优电感值可以在[0.90 H, 1.05 H]中取值,与330 Hz处的结论相同。

图11 1 100 Hz处不同电感值下结构传递曲线图Fig.11 Structure transfer curve at 1 100 Hz with different inductance values

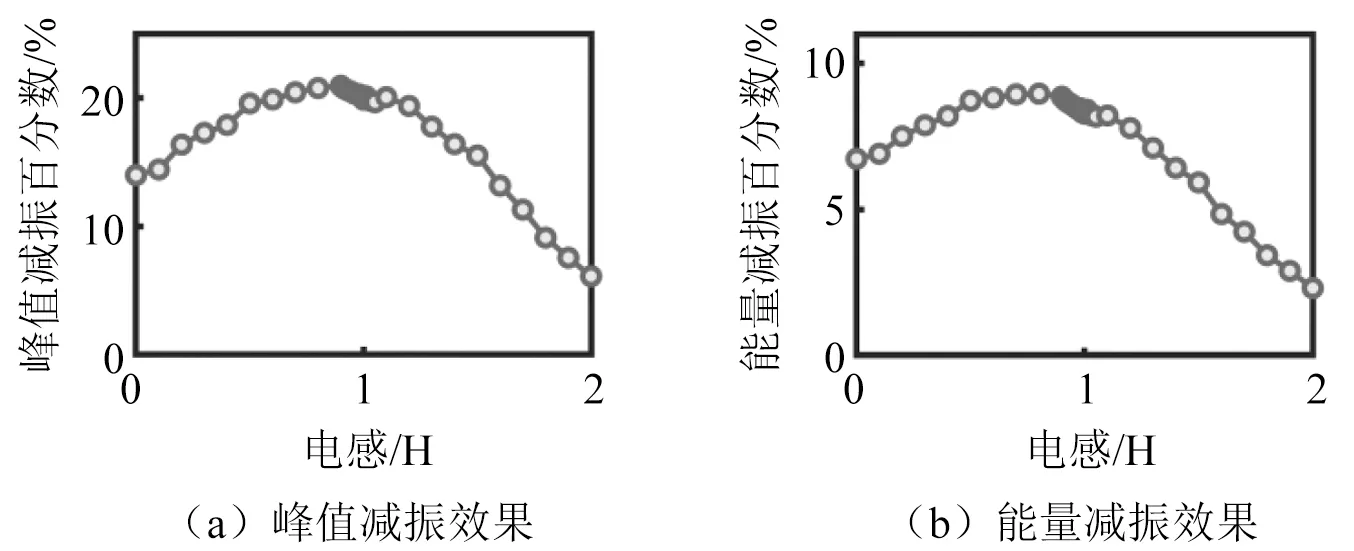
图12 1 100 Hz处减振效果随电感变化图Fig.12 Diagram of vibration reduction effect varying with inductance at 1 100 Hz

3 单压电片多模态减振试验研究

3.1 多模态电路原理

研究表明[31],压电片能够实现两阶或更多阶模态的共同减振,相关学者也实现了多模态共同控制的电路,其原理如图13所示。

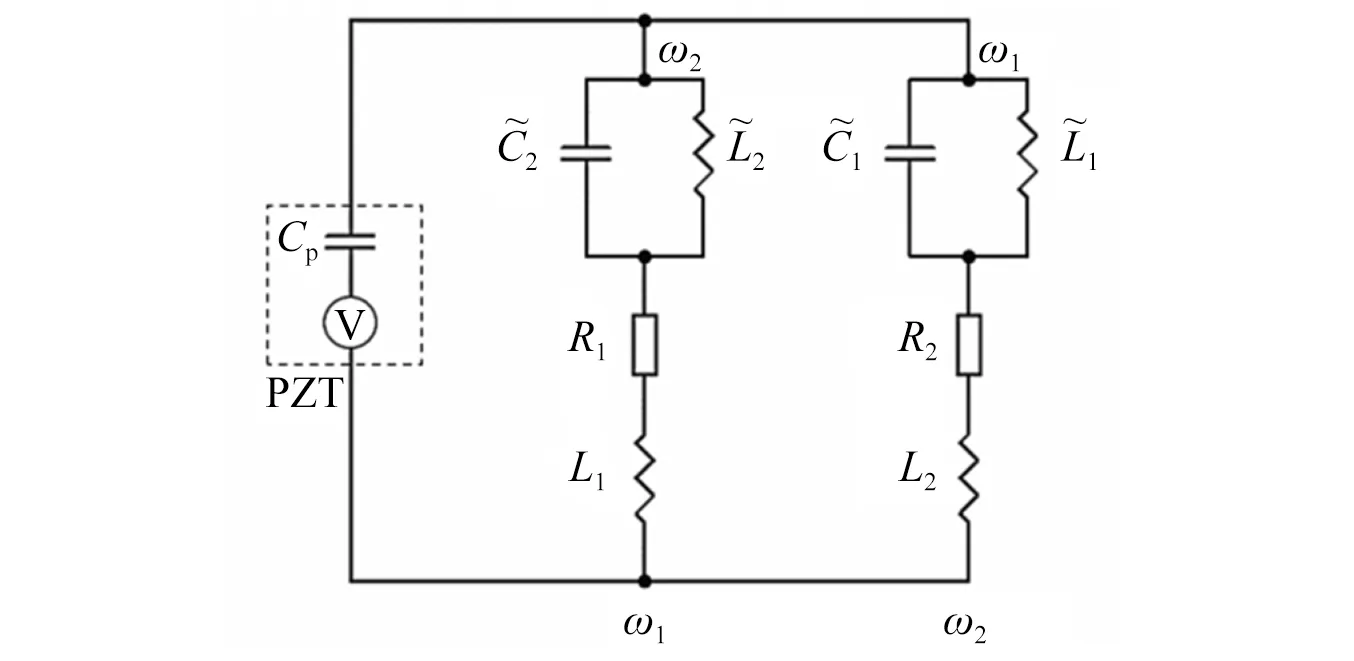
图13 多模态电路示意图Fig.13 Multimodal circuit schematic diagram

在多模态电路中,每一个支路都额外设置一个电感和电容进行阻塞,使每一个分支电路仅对应一个模态频率进行减振,用以减振的电阻和电感仍由式(1)、式(2)进行计算,隔流电感的计算如式(3)所示

(3)

3.2 多模态减振试验

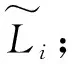
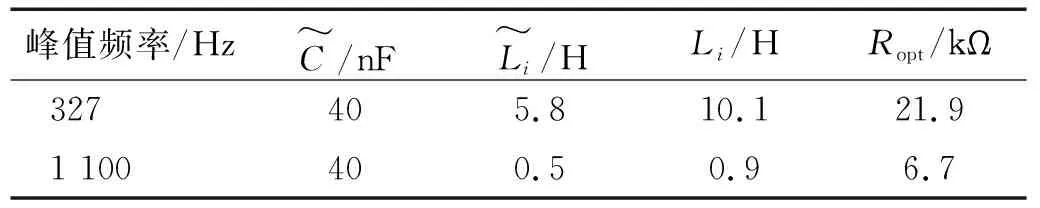
表2 UL压电片多模态电路参数Tab.2 Multimodal circuit parameters for UL piezoelectric plate

把多模态电路搭建完整后接入压电元件两端,进行扫频试验。在330 Hz处,多模态电路与单模态电路的结构动力学响应传递曲线如图14(a)所示。与开路相比,330 Hz单模态电路下330 Hz处峰值和能量分别降低24.8%和13.7%;1 100 Hz单模态电路下330 Hz处峰值和能量分别降低17.8%和12.6%;多模态电路下330 Hz处峰值和能量分别降低21.5%和13.0%。具体的减振效果如表3所示。

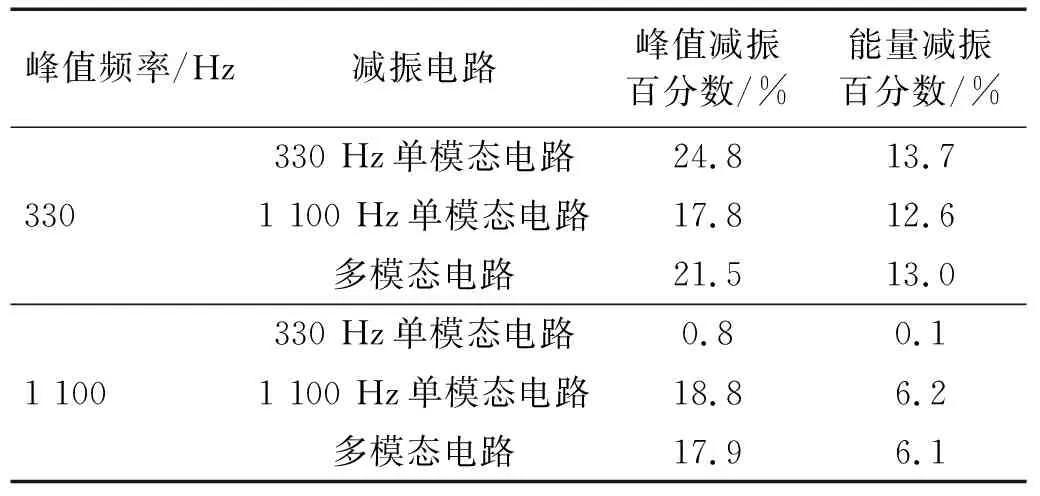
表3 UL压电片多模态电路减振效果Tab.3 Vibration reduction effect of multimode circuit with UL piezoelectric plate

图14 UL压电片多模态电路下结构传递曲线图Fig.14 Structure transfer curve of UL piezoelectric plate multimodal circuit

在1 100 Hz处,多模态电路与单模态电路的传递曲线如图14(b)所示。与开路相比,330 Hz单模态电路下1 100 Hz处峰值和能量分别降低0.8%和0.1%;1 100 Hz单模态电路下1 100 Hz处峰值和能量分别降低18.8%和6.2%;多模态电路下330 Hz处峰值和能量分别降低17.9%和6.1%。具体的减振效果见表 3。

此外,本节还选取了808 Hz和1 733 Hz两个频率进行多模态减振试验,减振压电片为UR压电片。通过式(1)～式(3)计算出UR压电片多模态电路参数后开展扫频试验,试验结果如表4所示。

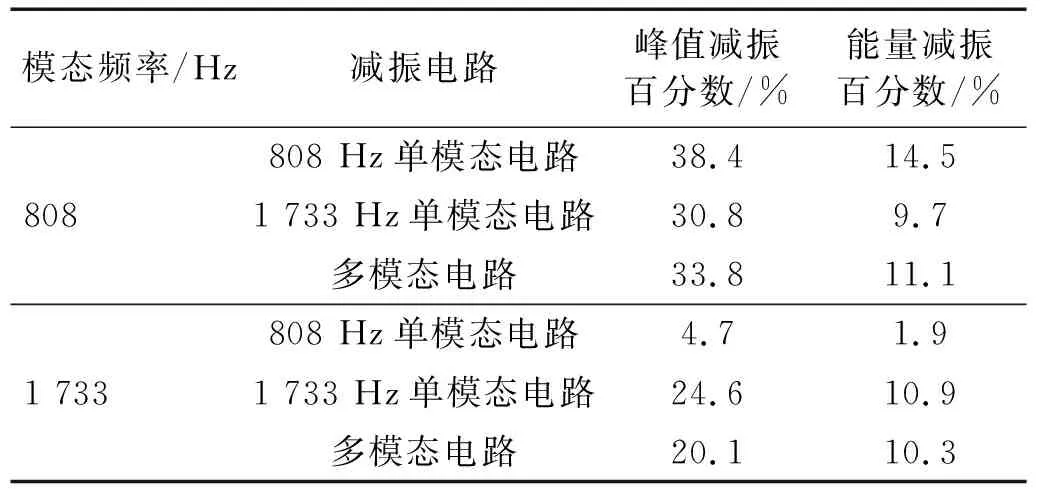
表4 UR压电片多模态电路减振效果Tab.4 Vibration reduction effect of UR piezoelectric plate multimodal circuit

结合以上两组多模态试验可以发现,阻塞电路成功地实现了多模态减振,能够在两个峰值的部位同时实现减振效果,但是与只有单模态电路时进行对比,减振效果有所降低。

4 多压电片多模态减振试验研究

4.1 模态试验

一个压电元件可以实现多模态减振,而压电元件能够对哪几阶模态起到减振效果,与粘贴位置和振型位置的对应关系有关[32-35],鉴于此本文首先进行模态试验得到2 000 Hz以内结构的模态振型信息。

本文模态试验采用移动力锤法,最终得到2 000 Hz以内的多个模态的频率和振型,部分结果如图15所示。

图15 铝板结构模态振型(部分)Fig.15 Mode shape of aluminum plate structure (Part)

4.2 多压电片多模态减振试验

在宽带扫频激励下开展多压电片多模态电路的减振试验研究。针对图15所示的模态振型结果,压电片选择图2(b)中的UL、UC、UR、MR、DL、DR,共六片压电片,多压电片多模态电路参数如表5所示。

表5 多压电片多模态电路参数Tab.5 Multimodal circuit parameters of multiple piezoelectric plates

将电路按照表中的参数搭建完整,接入各个压电片的两端进行试验,最终得到20～2 000 Hz以内的减振曲线如图16所示,对应各峰值减振效果如表6所示。从图16和表6 中可以看出,在808 Hz,1 100 Hz,1 736 Hz处,多压电片多模态电路起到了比较好的减振效果,但是在1 048 Hz,1 267 Hz,1 476 Hz,1 568 Hz处减振效果却较差。这是因为铝合金板高频时呈现出局部振型,如图15(f)～图15(h)所示,压电片粘贴时没有准确且完整覆盖在局部模态表面,导致减振效果没有达到最佳。

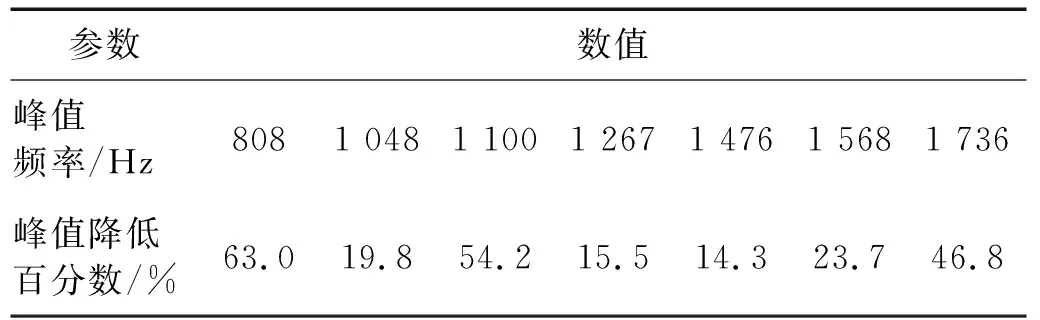
表6 多压电片多模态减振效果Tab.6 Multimodal vibration reduction effect of multiple piezoelectric plates

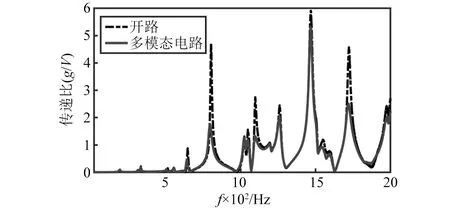
图16 多压电片多模态减振曲线Fig.16 Multimodal vibration reduction curve of multiple piezoelectric plates

此外,分别计算图16中开路和多模态电路的能量减振效果,可以发现多模态电路使振动能量降低了20.2%,可以在20～2 000 Hz频段实现较好的减振效果。

5 噪声激励下减振效果试验研究

5.1 噪声激励试验方案

在实际的工程应用中,规则的扫频信号激励几乎不存在,所以进一步选择用噪声载荷来模拟壁板结构的实际工况,从而进一步探究多压电片多模态电路的减振效果。噪声试验装置如图17所示,试验中选择用喇叭作为声源来激励铝合金板,试验时长为120 s,噪声载荷的声压级如图18所示。

图17 噪声试验现场图Fig.17 Diagram of noise experiment equipment

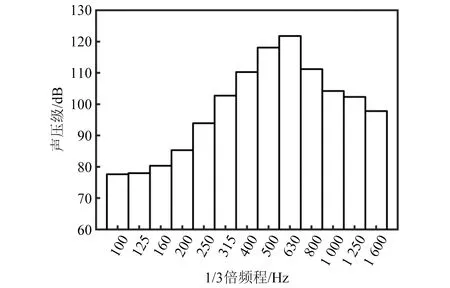
图18 噪声激励条件Fig.18 Noise excitation condition

5.2 噪声激励多模态减振试验

噪声试验时选用的压电片为图2(b)中的UL、UR、DL、DR四片压电片,每个压电片布置的电路参数如表7所示。

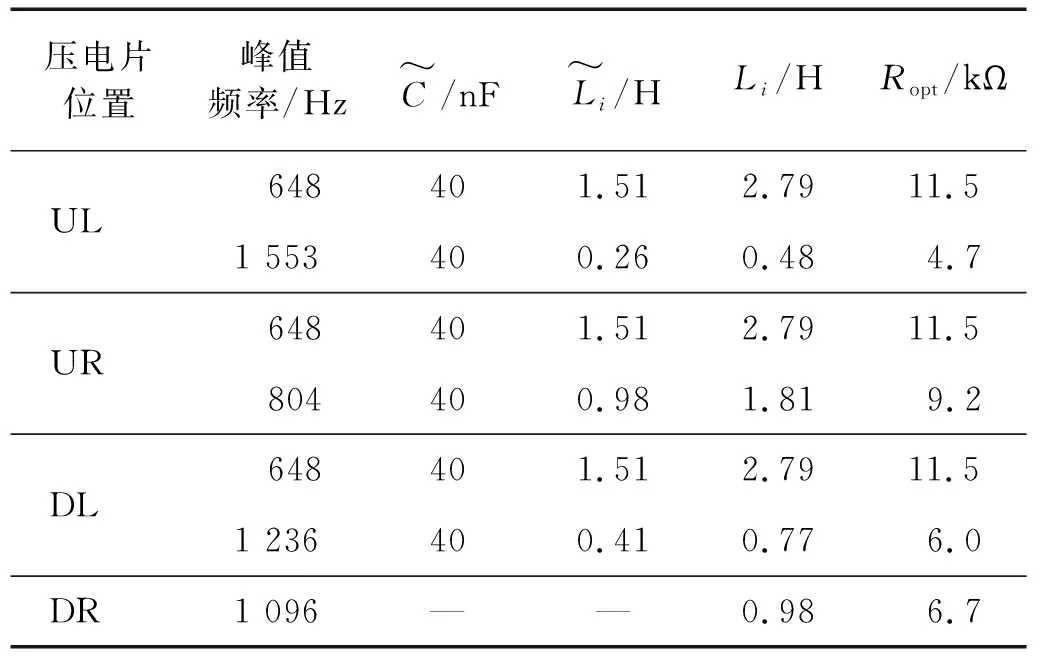
表7 噪声激励试验电路参数设置Tab.7 Noise excitation experiment circuit parameter setting

按照图17所示搭建试验系统进行试验,采集开路和多压电片多模态电路下结构的振动响应,比较3个加速度传感器采集到的信号,其中传感器#1的时域信号如图19(a)所示,对其进行傅里叶变换得到频域结果,如图19(b)所示。试验结果显示,在20～2 000 Hz内648 Hz是振动幅值最大的峰值,占据了大部分振动能量,所以多模态电路参数设计时着重对648 Hz进行减振。

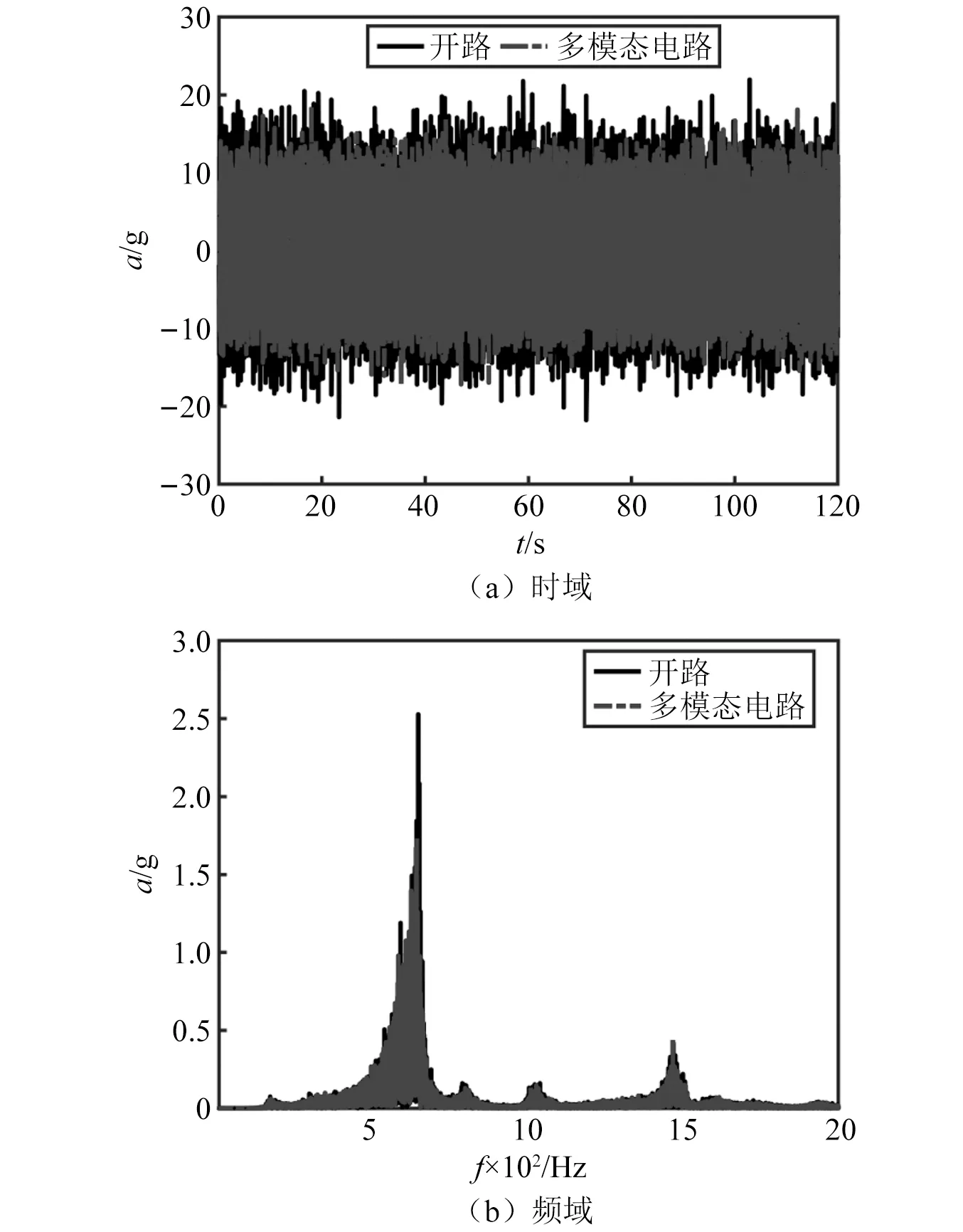
图19 噪声激励下传感器#1的加速度时域信号及频域结果Fig.19 Time domain signal and frequency domain result of acceleration under noise-excited sensor #1

通过计算传感器#1时域信号的均方根(root mean square,RMS)值,对比得出多模态减振使RMS值降低19.1%,而在频域下648 Hz处峰值下降了34.1%。3个传感器的具体减振效果如表8所示,可以看出在噪声激励下多压电片多模态电路可以起到良好的减振效果。

表8 各传感器减振效果Tab.8 Vibration reduction effect of each sensor 单位:%

6 结 论

本文以试验形式探究了压电分流阻尼技术对框架薄壁类结构的被动减振效果。试验通过从单压电片单模态电路减振逐步扩展到多压电片多模态电路减振,在扫频激励下研究了压电分流阻尼技术的减振能力;最后在噪声激励下对多模态电路减振效果进行了试验研究,验证了压电分流阻尼技术在实际工程载荷下进行减振的可行性。

(1) 本文首先在单模态频率下开展纯电阻电路和电阻电感电路的减振试验研究,电路最优参数的试验结果与理论结果保持一致。此外试验结果还表明,电阻和电感的最优值都可以在一区间内取值,而不需要与理论计算值保持绝对一致,这一结论表明单模态电路具有良好的工程实用性。

(2) 本文在单模态电路的基础上,采用阻塞电路成功实现了多模态频率的减振,并且采用多个压电片同时对20～2 000 Hz频段内多个模态频率进行减振。试验结果表明808 Hz,1 100 Hz和1 736 Hz处峰值分别降低了63%,54.2%和46.8%,其他频率处峰值至少降低14%,不同频率处减振效果的差异性主要由压电片位置与模态振型的耦合度不同导致的。此外,在20～2 000 Hz整个频段上振动能量下降20.2%。

(3) 本文最后在噪声载荷下开展了多模态电路减振试验研究。在20～2 000 Hz频段内3个不同位置处的加速度响应RMS值分别降低19.1%,18.2%,15.3%;在振动能量最明显的648 Hz处,峰值分别降低了34.1%,33.3%,31.0%。这一结论表明多模态电路在实际工程载荷下仍然具有减振的能力。