基于MSET重构模型整体优化的轴承性能退化评估方法

张 龙, 刘杨远, 吴荣真, 王 良, 承志恒, 颜秋宏

(华东交通大学 载运工具与装备教育部重点实验室,南昌 330013)

轴承的性能从健康到失效是一个渐变的过程,性能退化评估不仅是对该过程实现定量评估的有效手段,而且是实现轴承故障预诊断的前提与基础,更是发挥状态预测维修潜力的重要一环[1]。

轴承性能退化评估的一般流程为特征提取、特征选择、建立劣化指标、比较实测样本与无故障基准之间相似性[2]等几个方面。其中比较度量相似性方法又可分为基于边界的检测方法、基于概率密度估计和基于模型重构的检测方法3个方面。典型的边界检测方法有支持向量机[3]和支持向量数据描述[4],该类方法通过无故障训练数据集来创建边界,使用待评估数据与边界的距离确定其相对于无故障状态的类隶属。但是基于边界的异常检测方法问题在于距离指标的上限难以界定,从而难于从退化指标中定量推断性能退化程度。基于概率密度估计的方法一般使用高斯混合模型[5]和隐马尔科夫模型[6],该类方法首先对训练期间的无故障数据进行概率密度建模,之后将待测数据输入到训练好的模型中,样本若落入低密度区域则不属于无故障样本。但是,高斯混合模型假设无故障数据的概率密度分布可由多个高斯分布组合得到,其独立高斯函数数量难于精确估计,不能保证与实际情况完全相符;而对于复杂的系统而言,隐马尔科夫模型利用指数表达形式模拟健康状态区间,该策略与现实情况相违背,往往导致精度较低。

基于模型重构的方法通过映射目标数据集,将待测数据输入到经过无故障数据训练的模型进行映射,其重建误差大小(例如欧几里德距离)与退化性能程度密切相关。多元状态估计(multivariate state estimation technique, MSET)就是一个典型的基于模型重构的性能退化评估方法,本质上是一种非线性的多元预测诊断技术,也可称为一种非参数建模方法。MSET通过对健康状态基准进行相似性建模,然后输入待测的观测向量进行模型重构,比较度量前后差异性从而判断目标的性能退化程度。例如Wang等[7]将最大条件互信息(conditional mutual information, CMI)特征选择算法应用于MSET的训练数据,用K近邻算法(K-nearest neighbor,KNN)动态存储历史记忆矩阵,成功实现了风电机组性能状态检测。MSET重构模型相比于基于边界和概率密度估计的性能退化方法优势明显,其模型简单且物理意义明确,能及时准确地反映设备性能退化趋势。

在性能退化特征提取和选择时,常用的方法有时域、频域特征提取、小波特征提取和时序模型分析等等。崔凯等[8]将加速度有效值、峭度值两个时域指标结合在一起联合判断风机轴承运行状态。Zhou等[9]采用轴承信号小波包能量熵作为原始特征,然后将全寿命数据输入到利用健康状态特征建立好的RBF网络模型中,从而得到性能退化指标。Cong等[10]利用基于时序模型中的自回归模型(AR模型)和Kolmogorov-Smirnov检验相似概率值来反映滚动轴承性能劣化的趋势。但上述传统的单个域指标特征提取效果单一,对状态变化感知不明显,无法有效囊括轴承性能状态且不利于早期故障的发现。

许多研究将多域特征指标融合进行性能退化评估,例如Liu等[11]从轴承振动信号中提取多域统计特征,然后利用核联合特征矩阵近似对角化算法将其融合为敏感特征,最后计算健康数据和当前数据的类间和类内离散度作为性能退化指标。对于将多域特征组合的方法,虽然相较于单域指标能更细致地描绘轴承退化过程,但是高维特征存在信息冗余且计算量大的问题,从而降低性能退化评估模型的性能。Dong等[12]将时域、频域、时频域特征利用主成分分析(principal component analysis,PCA)降维后作为性能退化指标。丛华等[13]采用遗传算法(genetic algorithm,GA)优化提取特征,然后计算特征与支持向量数据描述超球体模型间的距离从而评估轴承的性能退化程度。然而,①PCA降维与其他优化算法不同,并非直接从高维特征中挑选出具有代表性的低维特征,而是利用空间转换将高维空间映射成低维空间,导致破坏了原有数据的结构,改变了原有数据的物理意义;②利用PCA或者GA单纯对输入特征进行降维或优化虽然一定程度上减少了冗余信息,但传统的时频域特征降维后的指标不一定适配所需模型,匹配度有待进一步考量。而目前做联合降维性能退化评估的长短期记忆网络[14-15](long short-time memory, LSTM)等参数过于复杂,时间跨度大且网络较深,导致计算量大且耗时费力。

综上,本文提出一种基于MSET重构模型整体优化的轴承性能退化评估方法。首先,基于轴承振动信号提取m组时域和频域特征、n阶AR模型系数和k维三层小波包Renyi 熵归一化后组成m+n+k维多域特征向量指标,并将得到健康状态的高维特征向量构建MSET模型的历史观测矩阵;然后,利用遗传算法对轴承高维特征向量和多元状态估计中的历史记忆矩阵的观测向量个数和维度进行同步联合优化,从而得到低维特征向量和历史记忆矩阵观测向量个数与该低维特征向量最匹配的MSET 模型,实现了特征优选和滚动轴承性能评估模型的整体自适应优化;最后,构建余弦相似度劣化指标实现轴承性能退化评估。

1 理论基础

1.1 小波包Renyi熵

小波包相较于小波而言,在信号高频部分分解得更加精细,能更好地刻画信号的突变性和非平稳性。其本质就是集合数个高低通滤波器从而将频谱划分多个层次,得到相应的高低频成分,更好地表达信号。其分解所得的频带之间没有疏漏和冗余,相互独立。

小波包分解表达式[16]如下

(1)

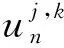
小波包重构表达式如下

(2)

小波包变换实际上就是小波基函数与信号进行卷积的过程。卷积在时域中的表现形式为移动的内积,从而使基函数和信号之间相似部分放大,反之则被抑制,因此小波基函数的选择将直接影响最后结果。信号进行j层小波包分解后将分成2j个子带信号。Nikolaou等[17]提出选择3层或4层小波包分解时,对所得到的信号分析结果影响不大。因此,为提高计算效率,本文采用db5小波基函数,对信号进行3层小波包分解。

当设备发生故障后,信号的不确定信息及能量分布将较正常运转时发生改变,不同的故障类型以及不同程度的故障其能量分布更是不同。信息熵具有表征信号复杂程度的能力,信号随机性越高、越复杂时信息熵越大,反之信号越规则信息熵越小。

信息熵计算公式如下

(3)

Renyi熵作为信息熵概念的扩展,具有表征信号在时频分布特征的能力[18]。Renyi 熵较信息熵而言对信号细微变化更加敏感,尤其是在端点处,能够捕捉到随机变量在概率分布中的差异并进行放大。Renyi熵计算公式如下

(4)

式中,α≠1且α≥0。当α=0时Hα(x)取最大值,Markel等[19]对Renyi熵的α进行了研究,表明α=0.5为结果最优值,故本文α选为0.5。

1.2 AR模型

自回归模型(autoregressive model, AR)是一种随机信号参数化建模方法,常用于处理时间序列。AR模型利用有限的知识和自身的参数对前面多个观测值进行学习,从而对下一时刻的输出进行预测,其对系统状态变化极其敏感,且能表征系统状态特征。

取时间序列y(t),AR模型的分析阶数为p,则关于时间序列的p阶AR模型可以表示为

(5)

式中:L(t)为AR模型的残差;αj为第j项的系数。

残差L(t)为真实值和预测值两者间的误差,对于平稳信号L(t)主要表征白噪声。所以AR模型实际上就是调整模型参数使残差更接近高斯白噪声。本文选用最常用的最小二乘法来进行AR谱估计以及模型参数的选择,根据贝叶斯信息准则(Bayesian information criterion,BIC)确定模型阶数。可大致分为三步:

步骤1确定分析阶数p的范围继而调整AR模型,本文p分别取1,2,…,300;

步骤2通过最小二乘法分别求得各阶次下的自回归参数αj(j=1,2,…,300),构造式(5)所示的AR模型,进而得到残差L(t);

步骤3根据各阶次残差L(t)的BIC值最小原则,确定最优阶数。

1.3 多元状态估计

多元状态估计是一种非线性的非参数建模方法。MSET通过比较新输入数据与无故障时的健康数据,对各变量数据之间的内在关联做出判断,根据历史数据所获得的权值向量等知识对实际运行状态做出估计,通过残差比较估计向量与新输入的观测向量的相似性,从而对设备进行诊断。

假设在某一过程或系统中某个时刻tj有n个互相关联的变量,将其记为观测向量X(tj),如式(6)所示

X(tj)=[x1(tj)x2(tj) …xn(tj)]T

(6)

式中,X(tj)为tj时刻状态变量xi的观测值。

首先,通过一定的方法合理地挑选m列正常运行状态下的观测变量即可组成历史记忆矩阵Dn×m,如式(7)所示,从而完整地表示某一过程或系统正常运行状态下的整个动态过程,换言之D即是对设备正常运行数据的特征提取、选择、学习和记忆的过程。

(7)

式中:n为在某一时刻互相关联的状态变量有n个;m为取m个观测向量X(tj),即取m个时刻。

然后,假设在某一过程或系统中某个时刻模型的输入为观测向量Xobs,将其输入历史记忆矩阵D之后的输出为估计向量Xest。Xest是对输入Xobs的预测值,即对当前状态的估计。对于任一输入观测向量Xobs,MSET均对应生成一个m维的权值向量W

(8)

根据权值向量W对D中m个历史观测向量进行线性组合即可得到估计向量Xest,如下所示

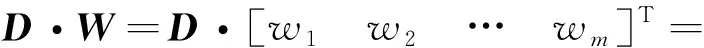
w1X(t1)+w2X(t2)+…+wmX(tm)

(9)

ε=Xest-Xobs

(10)

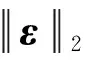
W=(DTD)-1DTXobs

(11)

在式(11)中由于Xobs的个数远大于监测系统参数个数,导致DTD不可逆,因此可采用非线性运算符代替普通矩阵乘积运算,即可得权重向量式(12)

W=(DT⊗D)-1·(DT⊗Xobs)

(12)

式中,⊗为非线性运算符,避免因变量之间的相关性造成矩阵点乘之后的不可逆现象,从而扩大关系式(12)的通用性。本文MSET重构模型采用两向量之间的欧式距离(Euclidean distance)作为非线性运算符

(13)

式中,xi和yi均为变量。

将式(12)代入式(9)可得估计向量的表达式

Xest=D·(DT⊗D)-1·(DT⊗Xobs)

(14)

式(10)、式(13)和式(14)的物理意义为:当新输入的观测向量Xobs仍然处于设备正常工作状态区间范围时,其与历史记忆矩阵D中某些观测向量的组合会很相似,欧氏距离会很小,导致输出的估计向量Xest预测值精度高,重构精度高,残差ε小;当新输入的观测向量Xobs为设备出现故障时,势必导致其动态特性发生变化,使Xobs偏离原始正常工作范围,从而无法利用D中某些观测向量的组合进行重构,两者相似度低,欧氏距离大,导致输出的估计向量Xest预测值精度低,残差ε大。由于Xobs和Xest两向量间的异同性包含丰富的运行状态信息,因此常利用二者间的残差进行故障模式识别或性能退化评估。

2 整体优化的性能退化评估模型

由上可知MSET重构模型能有效地获取故障信息并对性能退化程度进行评估。但应进一步考虑以下情况:①定量分析模型重构前后的残差从而对退化趋势进行量化描述;②确保高维多域特征经降维后得到的低维特征与MSET模型历史记忆矩阵中观测向量个数是匹配的;③设置合理的预警阈值从而对设备故障进行及时预警。这三点都是本文方法的关键所在,后续将进一步进行研究和分析。

2.1 试验数据分析

轴承在实际运行中,其故障的产生和发展是一个突发的、连续变化的过程,为了真实地反映故障连续变化的过程和验证本文所提方法有效性和可靠性,利用西安交大-昇阳科技联合实验室(XJTU-SY)所提供的全寿命加速疲劳轴承试验数据[20]进行分析。试验台如图1所示,包括驱动部分、测试部分和液压加载部分,具体器件如图中所示。DT9837采集器通过两个PCB 352C33单向加速度传感器对型号为LDK UER204的试验轴承进行信号采集,转轴转频为40 Hz,采样频率为25.6 kHz。试验设计了三种工况,每种工况有 5组测试轴承,工况类别见表1。

表1 加速疲劳试验工况Tab.1 Accelerated fatigue test condition

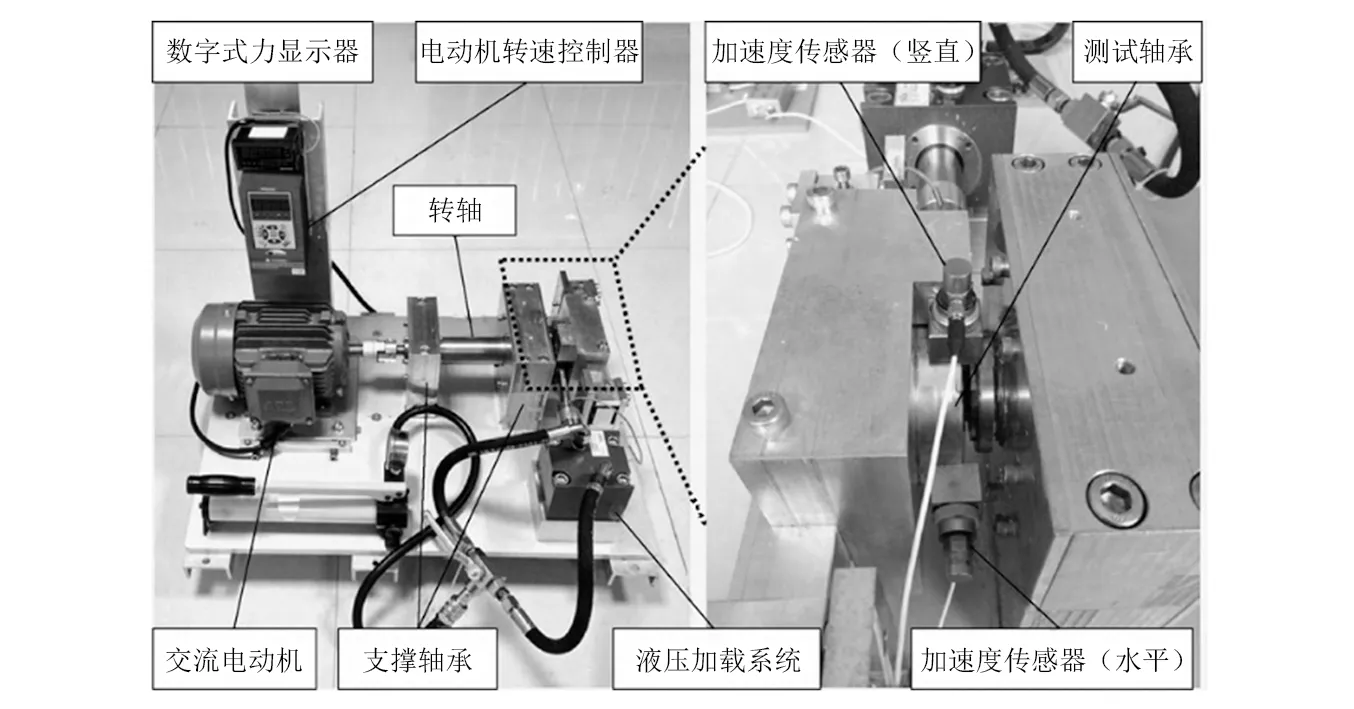
图1 XJTU-SY试验台Fig.1 The XJTU-SY test rig

本文以工况3第一个轴承Bearing 3_1为例进行分析,该轴承从开始运行到出现外圈故障直至失效累计时长42 h 18 min,试验中每隔1 min采样1.28 s数据,共计2 538组数据,每组数据32 768个点,图2为该轴承全寿命时域波形图。利用轴承故障特征频率计算公式所得的轴承各元件故障频率如表2所示。

表2 故障特征频率Tab.2 The fault characteristic frequency 单位:Hz

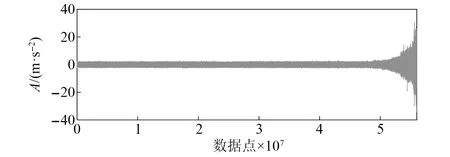
图2 轴承3_1的时域振动信号Fig.2 The temporal vibration signal of bearing 3_1

由前言可知,不同域的特征包含滚动轴承振动信号在不同状态空间的信息,例如表3所示的11个时域特征中绝对平均值、标准差、均方根值和峰值4个指标反映时域信号的能量大小,其余7个指标反映信号在时域的分布特征。而为尽可能地反映轴承信号在频域中所包涵的信息,取表4中13个常见的频域统计特征,其中序号1的特征反映信号在频域中振动能量大小,序号2～9的特征反映频谱的集中程度,序号10～13的特征反映主频带在频谱中的位置变化。

表3 11个时域特征指标Tab.3 11 time domain characteristic indexes

表4 13个频域特征指标Tab.4 13 frequency domain characteristic indexes

对各样本提取AR 系数特征时,AR 模型阶数的确定至关重要,阶数过低则无法准确对模型进行描述,反之则会导致过拟合,本文利用常见的BIC 准则对阶数进行确定。Bearing 3_1轴承全寿命周期2 538 min,本文认为试验刚开始时的前60 min为设备开机后的磨合阶段,试验数据不准确,于是取第61～第80共 20组测试轴承正常运行下的寿命信号分别计算其AR 最优阶数,由图3可知,最优AR 模型阶数为26阶,所以后续使用该轴承数据做故障诊断提取AR 系数特征时,一律取26阶AR 模型系数。

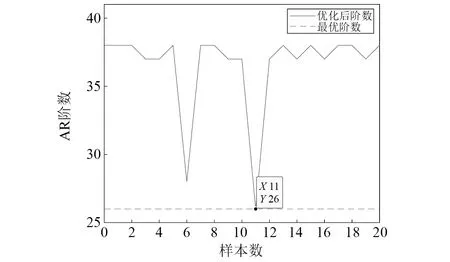
图3 20个无故障信号的最优阶数Fig.3 Optimal orders of 20 bearing signals without faults

由1.1节可知,信号数据进行j层小波包分解后将分成2j个子带信号,所以三层小波包分解将产生8个子带信号,依次对每个子带信号计算其Renyi 熵,即可组成一个8维三层小波包Renyi 熵特征向量。

综上,本文采用上述24组时域和频域特征、26阶AR模型系数和8维三层小波包Renyi 熵归一化处理后共同组成58维多域特征向量指标。

2.2 性能退化评估模型

本文基于MSET重构模型整体优化的轴承性能退化评估模型如图4所示,具体步骤如下:

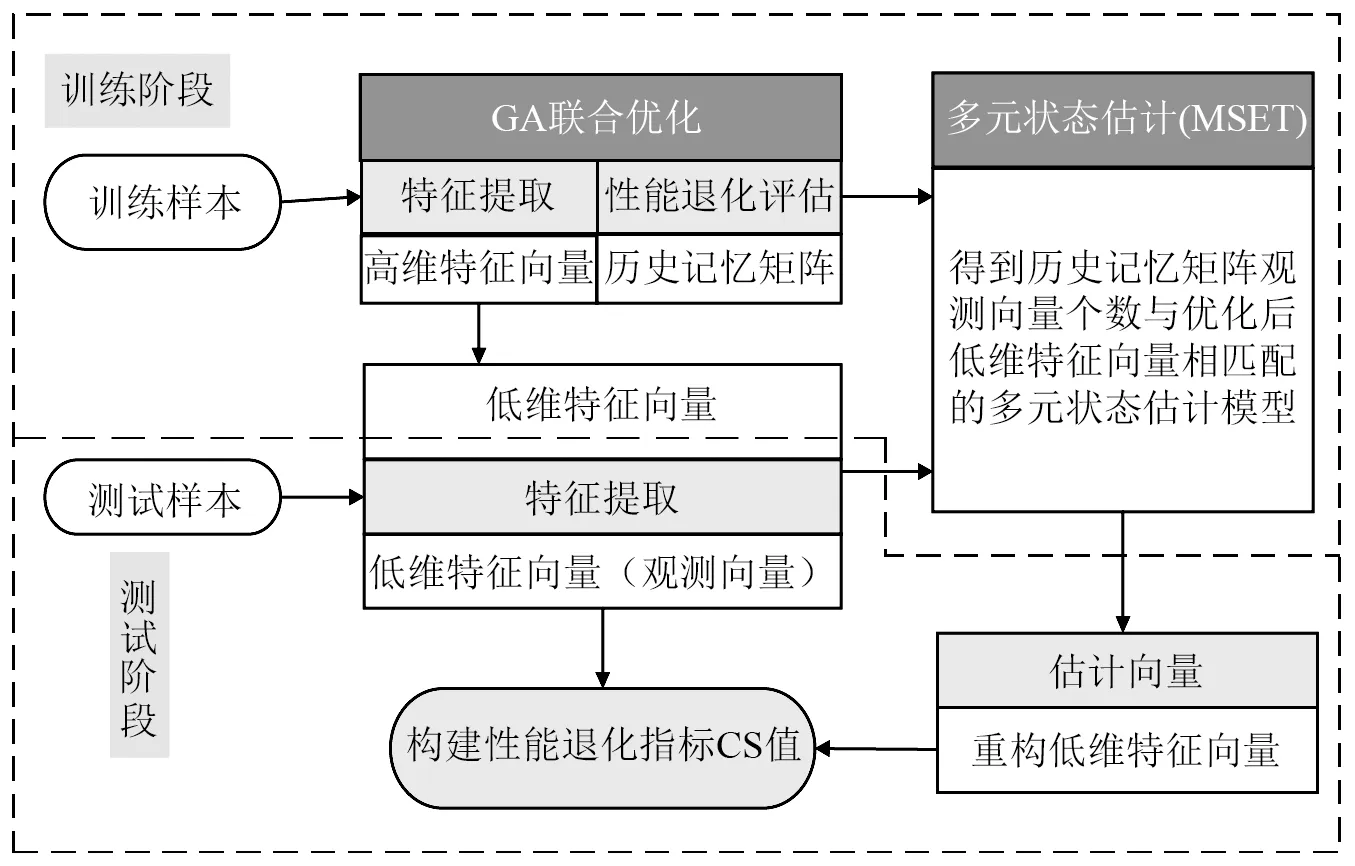
图4 性能退化评估模型Fig.4 Evaluation model of performance degradation

步骤1基于滚动轴承振动信号对原始时域数据提取24组时域和频域特征、26阶AR模型系数和8维三层小波包Renyi 熵归一化后组成58维多域特征向量指标;

步骤2利用滚动轴承正常运行状态下健康数据特征构建多元状态估计模型的历史记忆矩阵;

步骤3利用遗传算法对训练集高维特征向量和MSET中历史记忆矩阵的观测向量个数和维度进行同步联合优化,实现特征降维和个数优选;

步骤4对测试集数据提取低维特征,维度与GA优化后一致,将得到的测试样本低维特征向量作为观测向量输入MSET模型中;

步骤5输出估计向量,计算观测向量与估计向量之间相似性。

经MSET模型重构后的Xest为单重构的低维向量,并不能直接反映劣化程度,本文选用重构前后两向量之间的余弦相似度(cosine similarity, CS)作为性能退化指标,从两向量空间距离的角度评估滚动轴承性能退化程度,CS表达式如下

(15)

GA相较于粒子群优化[21]和模拟退火[22]等优化算法而言,对初始条件的设置要求较低,只需设定相应的适应度函数即可,具有较强的鲁棒性,能更快地搜索到全局最优解。上述步骤3中利用GA对模型进行同步优化的具体操作如下:

步骤1采用二进制编码方式进行编码,对测试轴承前n个样本和58维特征向量组成染色体长度为n+58的基因组,其排列方式如图5所示;

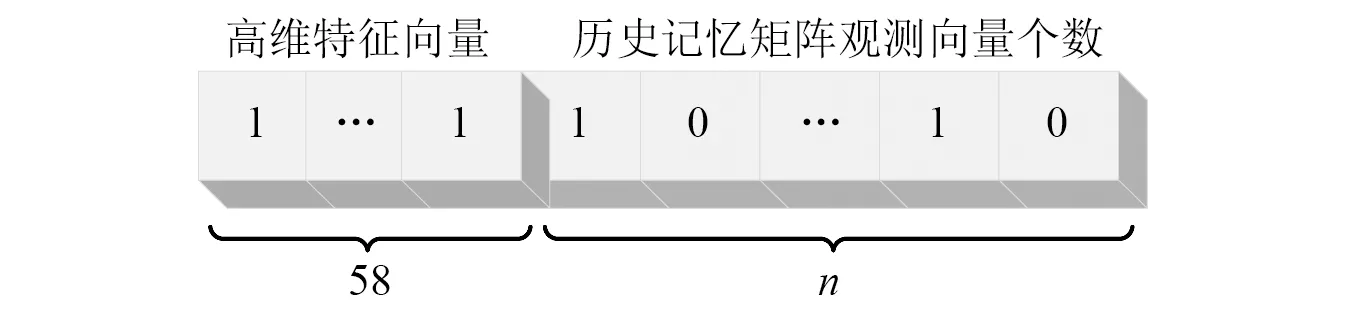
图5 编码排列方式Fig.5 Coding arrangement mode

步骤2初始化GA参数,设置初始种群大小为50,遗传代数为100,采用多点交叉方式,交叉率为0.7,变异率为0.05,代沟值为0.9;

步骤3设置训练样本集合,主要由无故障阶段和失效阶段两部分信号构成;并采用所有正常样本CS均值与所有故障样本CS均值的比值设计适应度函数,从而计算个体适应度,适应度越高,个体越优;

(16)

式中:m为正常样本数量;n为故障样本数量;CSN为正常样本的余弦相似度;CSF为故障样本的余弦相似度。

步骤4根据步骤2中所确定的交叉和变异遗传算子对当前种群进行处理,并判别其种群个体适应度是否达到要求。若达到要求则进行解码,得到最优低维向量的维数及其索引以及最优历史记忆矩阵观测向量个数和维度,执行步骤6,否则继续下一步;

步骤5进行选择、交叉、变异过程,返回步骤3;

步骤6获得最优参数建立MSET单重构模型,利用模型进行性能退化评估。

2.3 自适应预警阈值

余弦相似度CS是一条连续变化的曲线,将其作为劣化指标能准确地量化表征轴承目前运行状态与无故障运行时的偏离程度。进一步还需要对该曲线标定一个恰当的预警值从而及时对故障进行示警。

由统计学知识可知,数学期望为μ,方差为σ2的正态分布(μ,σ2)数据,样本数值落在(μ-3σ,μ+3σ)区间内的概率约为0.997 3,因此判定在样本故障程度相近时,CS值也符合正态分布要求。进一步当连续多个样本的CS值超过由历史样本CS值所确定的(μ-3σ,μ+3σ)区间范围时,判定该时刻故障程度于前一刻已经发生较大变化。CS值是连续单调递减的,故只计算下限μ-3σ即可,如式(17)所示。本文利用3σ准则对CS值进行预警值标定,未超过该值的视为正常运行状态,同时利用当前所有无故障样本更新CS值的3σ区间,达到自适应示警的目的。

式中:{D(i),i=1,2,…,n}为t=[1,n]时刻的CS值;T(t)为t时刻预警值。当首次连续多个CS值小于te时刻的预警值T(te)时,定义该时刻为早期故障时刻或故障程度加深时刻。为防止外界偶然因素的影响,本文早期故障时刻要求连续5个测试数据的CS值小于或等于te时刻的预警阈值。

3 试验结果分析

3.1 联合优化特征降维

对试验数据按照步骤1～步骤5进行整体优化性能退化评估操作,具体如下:首先从健康运行轴承的采集信号中选择300个样本提取其58维特征作为观测向量用来构造历史记忆矩阵D。然后额外选取100个正常运行状态的样本和100个故障样本提取其高维特征作为训练数据,利用遗传算法对训练集高维特征向量和MSET 模型中历史记忆矩阵的观测向量个数和维度进行同步联合优化。最后将Bearing 3_1 轴承全寿命周期2 538个样本作为测试数据,提取其低维特征,维度与GA优化后一致,将得到的测试样本低维特征向量作为新输入观测向量输入MSET模型中进行后续分析。

对试验数据进行样本划分后按上述过程进行整体优化性能退化评估,优化结果如图6所示。从图6(a)中可以看出,经优化后历史记忆矩阵所包含的观测向量个数由原始的300个变为133个,且分布较为均匀,有效地剔除了部分冗余观测向量,减少了后续性能退化评估的计算量;从图6(b)中可以看出,在步骤3同步联合优化中,58维特征优选成了9维特征,由小波Renyi 熵后三项和AR模型中6个系数组成,其中24组时域和频域特征降维成了0维,表明时、频域指标对西安交大轴承数据中的Bearing 3_1试验数据分析结果较差。

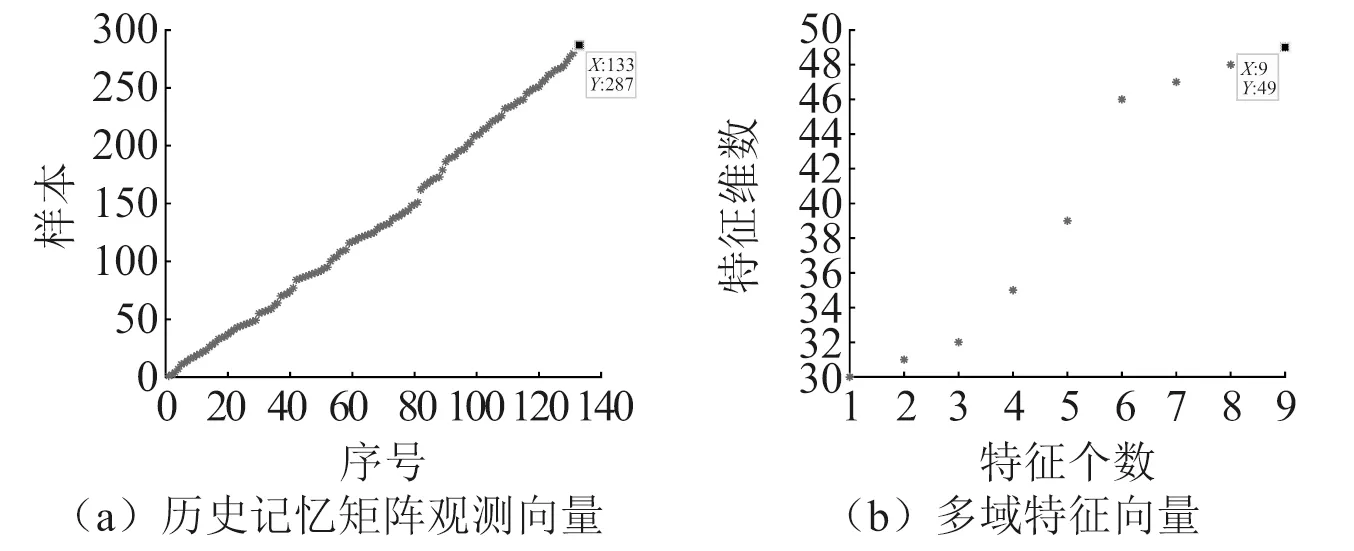
图6 优化结果Fig.6 Optimization results

为进一步分析该试验数据特征优选后时域、频域特征降维后变成了0维的原因,对3个时域指标和3个频域指标进行作图,如图7所示。从图7中可以看出,脉冲因子和峭度值与轴承故障发展趋势基本一致,但后期均出现先减小后增大的情况,与故障实际发展情况不相符,并且脉冲因子指标前期波动过大,不利于早期故障的发现;加速度有效值波形后期振荡过于严重,与故障实际发展情况不相符;其余3个频域特征均不能准确表征故障程度和性能退化趋势。

图7 轴承时域指标Fig.7 Time domain index of bearing

3.2 全寿命曲线

对Bearing 3_1轴承全寿命2 538个样本进行分析,性能退化评估CS 值曲线经过5点平滑处理后如图8所示。由于故障程度具有渐变性,平滑处理不仅不会影响故障预警,更能削弱噪声干扰,更好地表达信号。图中虚线为自适应预警值,实线为故障指标CS 值,曲线整体呈现下降趋势,表明CS 值能准确、一致地表征轴承故障严重度趋势,且相较于图7的时域指标对轴承早期故障更加敏感。

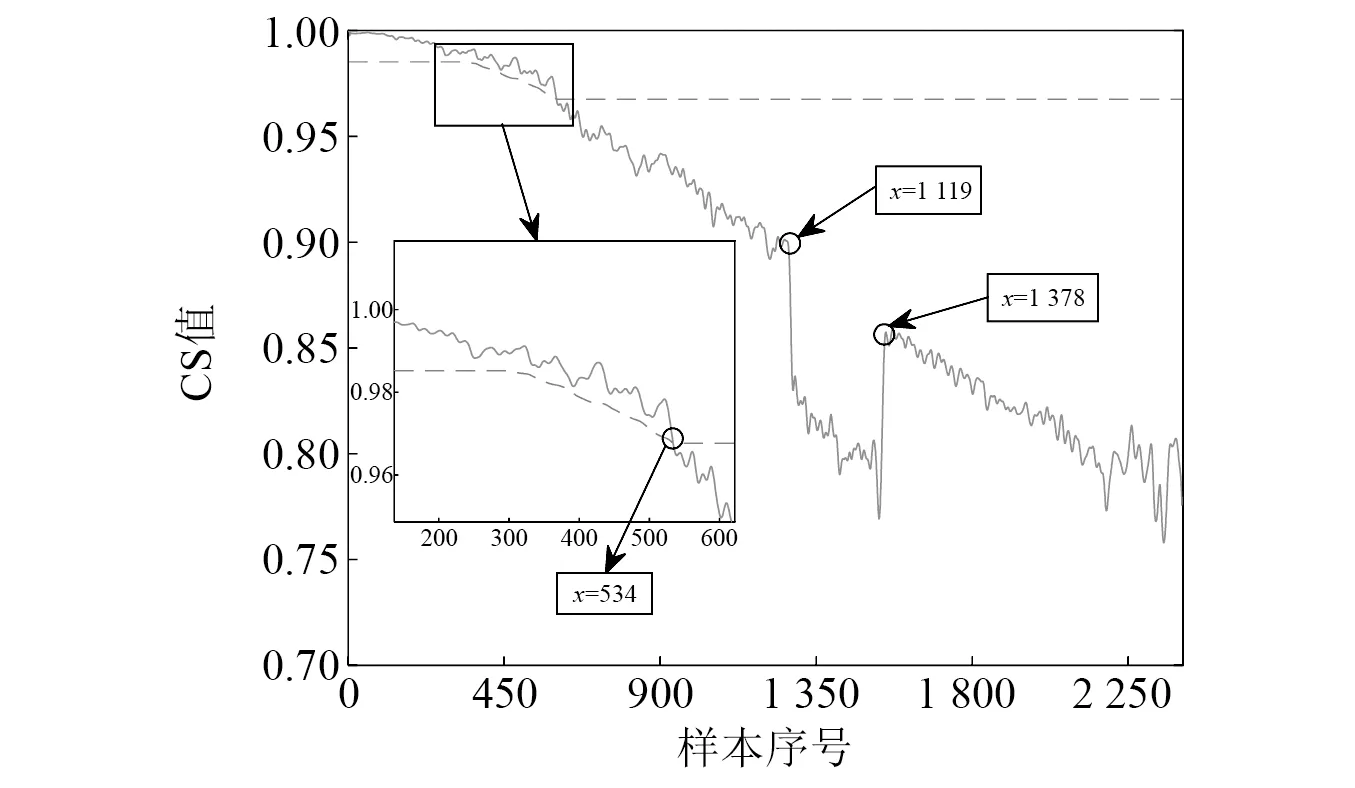
图8 轴承全寿命CS值Fig.8 CS value of bearing life

图8中性能退化评估曲线大致可划分成无故障时期、初始故障时期、中度故障时期和恶化失效时期4个阶段。由于该轴承的CS 值在534时刻起连续5个值小于自适应预警值,故0～533时刻为无故障时期,534时刻为初始故障发生时刻。534～1 119时刻内的CS 值呈明显下降趋势,但在1 119时刻曲线出现阶跃现象,CS 值急剧下降,这是因为该时刻轴承故障程度持续加重,导致新输入观测向量与历史记忆矩阵的偏离程度持续加深,最终在1 119时刻达到中度故障时期。1 119～1 378时刻内的CS 值振荡降低后垂直上升,这是因为故障的发展是一个渐变的过程,从微小故障逐渐扩大,然后磨平,随着时间增加故障再度扩大,所以导致CS 值出现了大范围地反复波动。1 378时刻,原始故障点已被磨平,因故障产生的突变冲击减小,新输入观测向量与历史记忆矩阵的偏离程度减小,CS 值突变增大。1 378～2 538时刻,轴承故障程度不断加重,且CS 值波动程度比之前各阶段更大,波动时间更短,表明故障点的“磨平- 恶化”情况更加明显,且故障程度快速加深直至轴承失效。从图中还可以看出,CS 值曲线整体毛刺较多,局部波动性大,这是由于轴承在整体运转过程中微小的“故障磨平、再度劣化”现象一直存在。

为进一步分析CS 值与故障程度之间的关联性,选取无故障阶段(0～533)、 轻度故障阶段(534～1 118)、 中度故障阶段(1 119～1 377)、重度故障阶段(1 378～2 538) 四种状态中各3个样本,计算其低维特征后输入联合优化模型,可得到输出估计向量与观测向量之间的余弦相似度差异,不同故障程度下CS 值的变化如图9所示。从图中可以看出,无故障样本的CS 值最大,3个样本的均值约为0.985,接近于1,这是因为无故障样本提取的特征与历史记忆矩阵中各向量相似程度高,输出估计向量与观测向量的偏斜度小,两空间向量之间的夹角小,余弦相似度大。而随着外圈故障尺寸的变大,估计向量与观测向量之间的CS值越来越小,这是由于随着故障严重度加深,轴承当前状态越来越偏离无故障运行状态,输入特征越来越偏离依靠健康样本所建立的历史记忆矩阵的观测向量,两者之间的偏斜度越来越大,在CS 值上的表现则呈现出递减趋势,从而很好地区分轴承的故障程度。

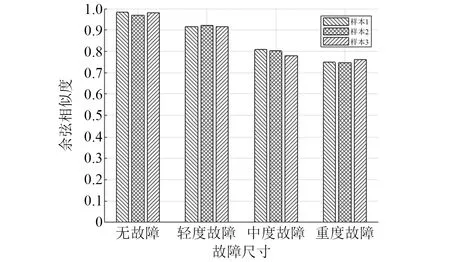
图9 不同程度外圈故障CS值Fig.9 CS value of outer ring faults in different degrees

4 试验验证及对比

4.1 试验验证

为验证联合优化多域特征-MSET 重构模型方法的有效性,对No.534和No.533样本信号进行以包络谱谱峰因子为优化指标自适应共振解调[23]处理,共振解调后对轴承信号进行傅里叶变换,如图10所示。

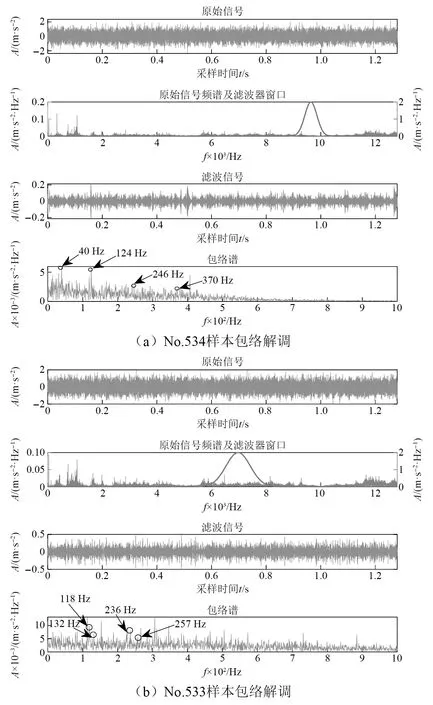
图10 故障样本包络解调Fig.10 Envelope demodulation of fault samples

图10(a) No.534样本共振解调结果中出现明显脉冲现象,且在频谱的包络谱中出现了与外圈故障频率BPFO(123.3 Hz)相近的一倍频124 Hz、二倍频246 Hz和三倍频370 Hz,此外转轴转频40 Hz也清晰可见。但由于该时刻为早期故障点,轴承外圈刚刚出现微小故障,导致二倍频和三倍频几乎泯没在噪声当中。而在图10(b)No.533样本包络解调中冲激现象和123.3 Hz的外圈故障频率成分并不明显,且在534时刻的最优滤波频带相较于533时刻的最优滤波频带发生了明显改变。因此,证明534时刻为轴承早期故障点,验证了方法的有效性和可靠性。

4.2 对比试验分析

为验证本文所提方法的优越性,首先采用仅进行特征维度优化的MSET轴承性能退化模型进行对比分析。利用GA对58维特征向量进行降维,如图11所示,从图中可以看出仅对特征进行优化时,时域、频域的特征向量仍有所保留,与图6的分析不相符,导致输入将含有许多冗余信息。进一步分析,将降维后的34维特征向量输入未经优化的MSET模型,其性能退化曲线和自适应预警值如图12(a)所示,其早期故障点为No.306样本,远远早于本文方法所判断的早期故障点,原因是因为未经优化的MSET模型历史记忆中的观测向量个数过多,而输入的特征向量维度也过多,导致含有许多冗余信息从而提前误判故障点。为验证该时刻轴承并未发生故障,对No.306样本信号进行包络解调,如图12(b)所示,其频谱中并无外圈故障频率成分,证明此刻轴承仍处于正常运行状态,并未发生故障,早期故障点判断失误。

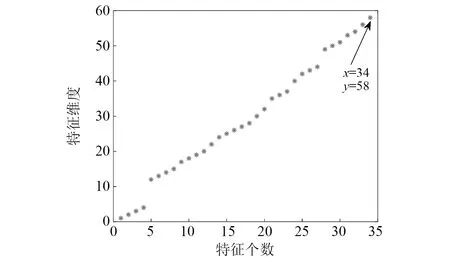
图11 多域特征向量优化结果Fig.11 Multi-domain eigenvector optimization result

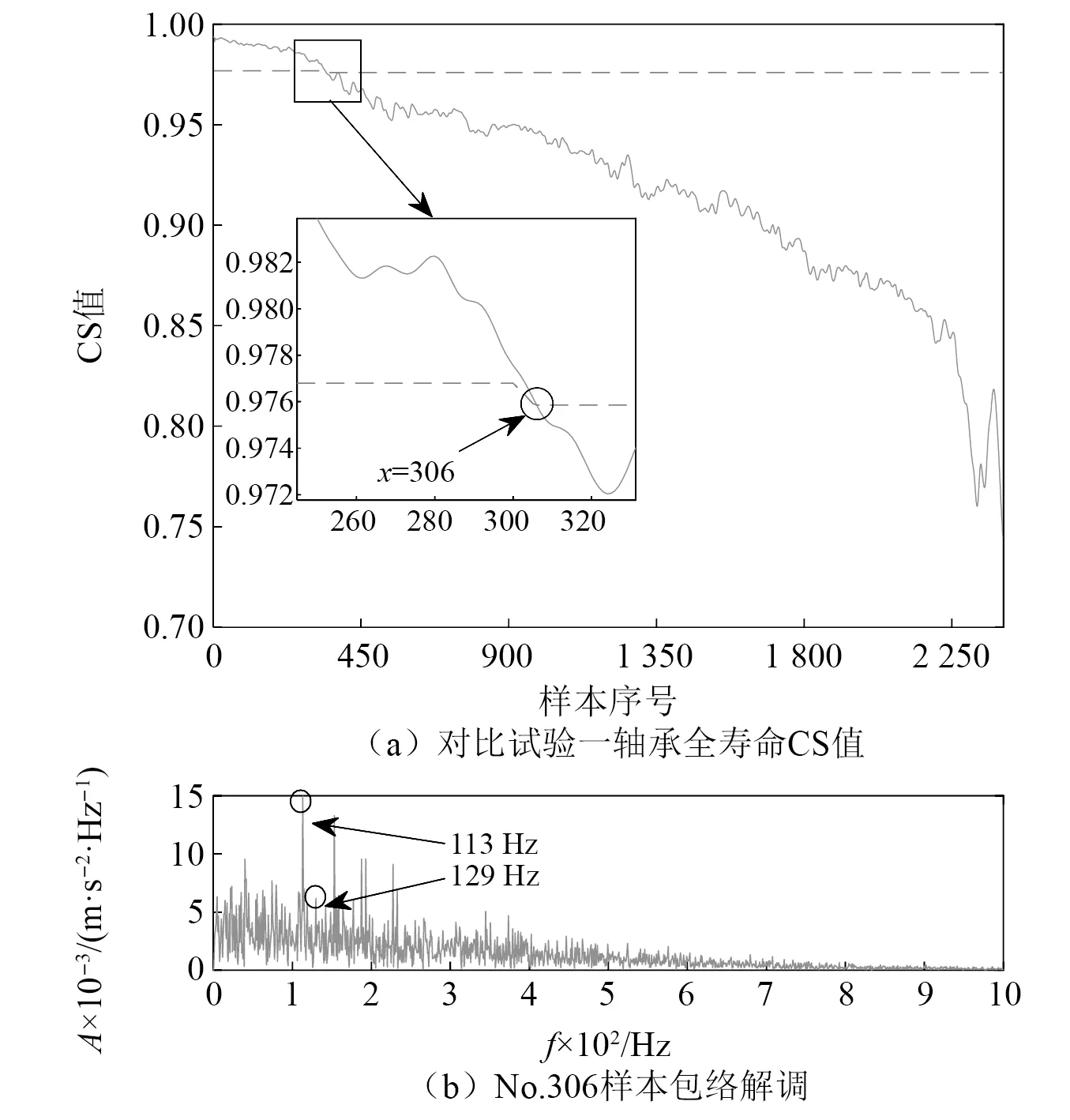
图12 对比试验一分析Fig.12 Analysis of the comparative experiment one

其次,采用仅优化MSET中历史记忆矩阵的轴承性能退化模型进行对比分析。利用GA对观测向量的个数进行优选后,如图13所示。从图13中可以看出,历史记忆矩阵观测向量个数由原来的300个变成了156个,分布较为均匀,有效剔除了冗余观测向量。进一步分析,将提取的高维特征向量直接输入优化后的MSET模型,其性能退化曲线和自适应预警值如图14所示。从图14中可以看出,在No.320样本处CS值曲线与自适应预警值曲线已有切点,预示轴承已经开始出现故障,但从图14(b)的包络解调结果可以看到该样本仅包含转频40 Hz,因此该预测结果不准确。而由于未对输入高维特征进行优化,导致性能退化曲线并不能很好地区分轴承的故障程度,自适应预警值也不能准确有效地反映出早期故障发生时刻,致使长时间后在No.2296样本处两曲线再次出现交点,而该时刻虽已发生故障,但远远晚于本文方法所判断的早期故障点,时效性不强,不具有使用意义。

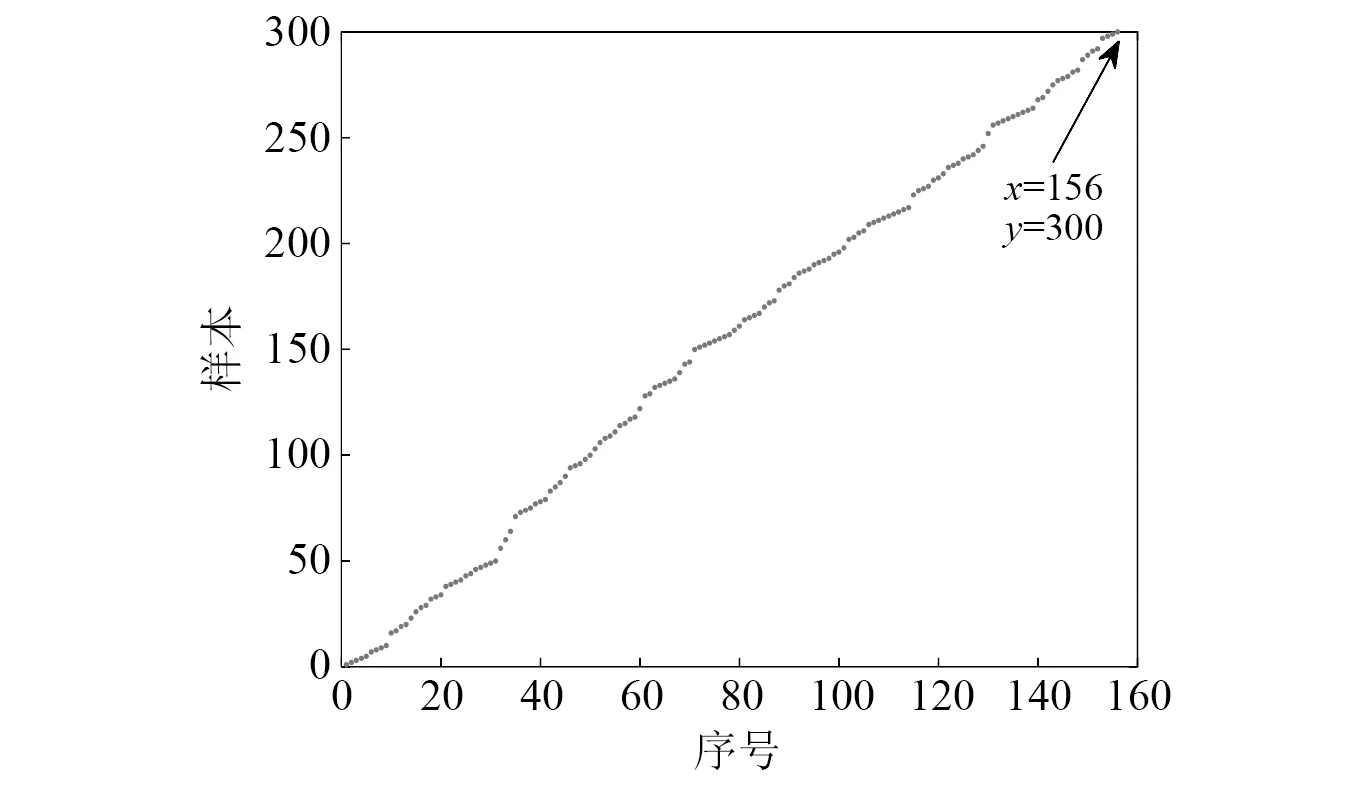
图13 观测向量优化结果Fig.13 Optimization result of observation vector

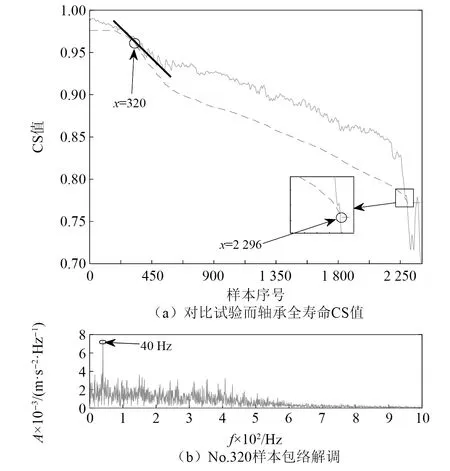
图14 对比试验二分析Fig.14 Analysis of the comparative experiment two

由以上两个对比试验综合分析可知,相比于本文所提出的联合优化多域特征-MSET模型,单优化输入特征维度和单优化历史记忆矩阵的模型效果均一般,与轴承的实际发展趋势不一致,不能及时地、准确地反映轴承早期故障,也无法很好地区分故障程度,由此说明本文所提的整体优化MSET单重构模型方法的准确有效性和优越性。

进一步为验证所提模型的泛化性和优越性,采用多个轴承全寿命数据进行性能退化评估,并与其他文献中结果进行对比。从表5中可以看到,所用方法在不同轴承数据集下均能更准确地判别轴承性能退化趋势,模型具有一定的泛化性。

表5 不同轴承数据间的试验结果Tab.5 The results between different bearing data

5 结 论

针对传统单域特征指标无法充分表征轴承状态信息,而目前性能退化评估中基于多域高维特征向量的重构评估模型存在信息冗余且易受到不一致优化目标的影响,不能在低维空间中保留必要的信息,而导致模型次优性能。提出一种基于MSET重构模型整体优化的轴承性能退化评估方法,通过同步联合优化多域特征和MSET 模型历史记忆矩阵从而实现特征优选和性能评估模型的整体自适应优化。

(1)XJTU-SY 轴承全寿命数据分析表明经联合优化多域特征-MSET 重构模型后的所得CS 值能很好地表达轴承故障严重度变化,且随着程度加深具有单调递减趋势;并通过对传统时域指标进行比较,表明本文所提方法对轴承早期故障更加敏感,且与故障发展趋势的一致性更好。

(2)通过对两组单优化对比试验和不同方法进行比较分析,并利用复小波共振解调法对早期故障点进行验证,表明本文基于MSET重构模型整体优化的轴承性能退化评估方法更具有效性、可靠性和优越性。