基于浸入与不变原理的水轮机调节系统簇发振荡控制

李冬航, 王 聪, 张宏立, 马 萍

(新疆大学 电气工程学院,乌鲁木齐 830047)

水轮机调节系统是由机械、电气、水力耦合的复杂非线性系统[1],凌代俭等[2]指出其调节对象具有非线性、最小相位特性;郭鹏程等[3-4]也论证了水轮机调节系统复杂的非线性动力学行为。由于其稳定性关系到整个水电机组甚至是电网的正常运行,因此,对水轮机调节系统进行非线性动力学分析并设计合理的控制策略具有重要的研究意义。

近年来,水轮机调节系统中混沌现象的分析和抑制问题受到越来越多的重视[5],许多先进控制理论被应用到其控制中。陈帝伊等[6]将滑模控制应用到混沌状态的水轮机调节系统中,消除了水轮机调节系统由于比例-积分-微分(proportion-integral-derivative,PID)参数选取不当而引起的混沌现象;王斌等[7]针对混沌状态的水轮机调节系统设计了终端滑模有限时间控制器,通过引入新的非奇异终端滑模面,克服了传统滑模面的奇异性问题;Rajagopal等[8]分析了分数阶水轮机调节系统中的混沌现象,通过引入模糊规则设计了模糊PID控制器,将水轮机调节系统控制在了稳态。

然而,在参数激励下或考虑其机械、电气、水力部分的响应速度时,水轮机调节系统是多尺度耦合的系统,受快慢动力学效应的影响,其极易产生簇发振荡行为[9]。Zhang等[10-11]通过将传递系数等效为周期激励或考虑水轮机调节系统机械部分的慢时间尺度,将原水轮机调节系统划分为两尺度耦合的系统,分析出水轮机调节系统存在快慢动力学行为;Li等[12]在此基础上进一步分析了高阶水轮机调节系统的簇发振荡现象。簇发振荡的存在会影响水轮机调节系统的稳定运行,但是以上研究大多是基于水轮机调节系统混沌现象的分析和抑制,且针对其簇发振荡的研究也局限于现象的分析,较少考虑簇发振荡的抑制问题。

针对上述不足,本文采用基于浸入与不变原理的自适应反步滑模控制策略抑制水轮机调节系统的簇发振荡行为。其中,滑模控制具有较强的鲁棒性,但是其良好的控制性能是通过控制量的高频抖动换取的,在实际应用中受到一定的限制。而反步法是基于Lyapunov函数逐步递推的控制方法,在设计上具有更大的灵活性且不存在抖振的现象。本文将两者结合[13]进行水轮机调节系统控制器的设计。自适应控制常应用于具有复杂扰动的非线性系统,但是传统的基于等价原则的自适应控制方法在系统的参数估计上具有一定的局限性。浸入与不变原理是通过对扰动估计误差建立流形并保持其吸引与不变来维持系统稳定的,其在电机、机器人、电力电子等领域的应用均取得了很好的效果[14-16],但在水力发电领域尚未应用。本文将这一思想应用到水轮机调节系统的参数估计中,在其参数的估计中引入的额外补偿项增加了设计的自由度且此补偿项的引入使得传统自适应方法中参数估计的积分作用转化为了比例积分作用,比例积分形式的补偿项使得对扰动估计的收敛速度不断提升,在提高参数估计的灵活性的同时也改善了系统的控制性能。本文所提出的控制方案保证了水轮机调节系统的稳定运行,为其簇发振荡的控制研究提供了一定的参考,具有重要的研究意义。

1 水轮机调节系统的建模及簇发振荡分析

1.1 两时间尺度水轮机调节系统模型

以刚性水击条件下的混流式水轮机调节系统为研究对象,其组成部分主要包括水轮机、发电机、液压随动系统和引水系统。水流经由引水系统到达水轮机,之后由水轮机将水流的势能和动能转化为机械能,再由发电机将机械能转化为电能馈入电网。其中,液压随动系统是负责驱动导水机构进而控制进入水轮机的水流大小以实现机组转速调整的装置。其在刚性水击时的非线性模型[17]如式(1)所示

(1)

由于液压伺服系统中惯性的存在,导叶开度的变化量明显慢于其他3个状态变量,因此,可以加入时间标度因子ε(0<ε<1)来建立两时间尺度耦合的水轮机调节系统无量纲模型如式(2)所示

(2)

1.2 水轮机调节系统簇发振荡分析

为了分析时间尺度对水轮机调节系统非线性动力学行为的影响,系统参数取值如表1所示。

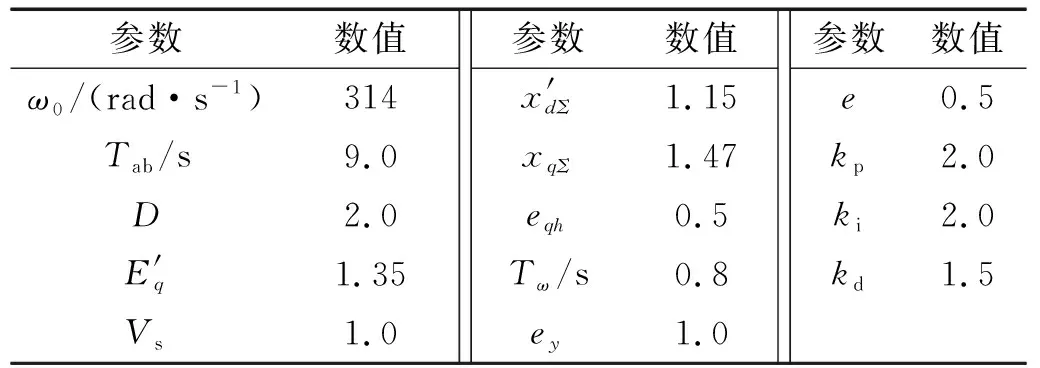
表1 水轮机调节系统参数Tab.1 Parameters of hydro turbine governing system

在MATLAB环境下对式(2)进行数值仿真。求解算法采用ode45,状态变量初值选取(0.001,0.001,0.001,0.001),迭代步长0.013,迭代次数4 200次。取ε=0.16进行仿真,相轨迹图和状态变量时序图如图1所示。

图1 水轮机调节系统快慢动力学行为Fig.1 Fast-slow dynamic behavior of hydraulic of hydraulic turbine governing system

观察图1可知,水轮机调节系统由于时间尺度差异而表现出明显的快慢动力学行为,转速相对偏差、机械力矩相对偏差、导叶开度相对偏差在时序图和相图中表现为沉寂态和激发态之间的来回转迁,经过6 s左右的振荡后即进入典型的周期簇发状态。其中,转速相对偏差和导叶开度相对偏差的高频振荡主要出现在峰值附近,而机械力矩相对偏差的高频振荡出现在额定值附近,且机械力矩相对偏差的波动范围更大。考虑到簇发振荡会影响水轮机调节系统的稳定运行,因此需要设计控制器来抑制此现象。

2 水轮机调节系统的控制器设计

反步控制的原理是把原高阶系统划分成多个低阶子系统,然后分别对各个子系统构造Lyapunov函数和虚拟控制量,最后再通过一步步反推来设计系统的控制律。但是单独的反步控制抗干扰性能较差,可以引入对不确定扰动的自适应律设计,同时加入滑模控制克服原系统的不确定性。

首先,将式(2)改写为严格反馈形式,如式(3)所示

2.1 自适应反步滑模控制器设计

通过分析上述系统的结构可知,控制状态变量δ,ω趋于稳定即可实现对整个水轮机调节系统的控制。所以,针对式(4)所示系统进行控制律的设计可以实现推导过程的简化。

(4)

式中:u为待设计的控制律;d为外部总扰动;f为中间变量,如式(5)所示

定义扰动估计误差

(6)

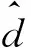
状态δ的跟踪误差

e1=δ-δd

(7)

式中,δd为状态变量δ的期望轨迹。

取其虚拟控制量

(8)

状态ω的跟踪误差

(9)

(10)

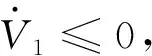
(11)

设计滑模面

s=λe1+e2

(12)

由式(12)可推出

(13)

取Lyapunov函数

(14)

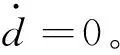
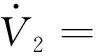
(15)

取控制器如式(16)所示

式中,系数h,η,σ均大于0。

将式(16)代入式(15),得

构造正定矩阵

(18)

可得

(19)

取扰动自适应律为

(20)

即可使式(19)非负,稳定性证明完毕。

2.2 基于浸入与不变原理的自适应反步滑模控制器设计

针对自适应反步滑模控制对扰动估计误差的动态变化不可调节的不足,引入浸入与不变理论,对误差估计建立流形如式(21)所示。

式中,β(δ,ω)为补偿函数。

若上述流形保持不变,则待设计控制器的系统方程可表示为

(22)

式中:w为自适应律;z为扰动估计误差。

只需设计合适的自适应律w和补偿函数β即可保证流形M的不变和吸引。其中,基于浸入与不变原理的自适应反步滑模控制器(immersion and invariance-adaptive backstepping sliding mode controller,I &I-ABSMC)的初始设计部分和2.1节式(7)～式(10)完全相同,结合式(22)可得

(23)

设计滑模面

s1=λ1e1+e2

(24)

由式(24)可推出

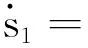
(25)

取控制器如式(26)所示

[hs1+ηtanh(s1/σ)]+ke1

(26)

对扰动估计误差z求导得

(27)

将式(22)代入式(27)得

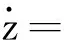
(28)

通过分析式(28),取扰动自适应律w为

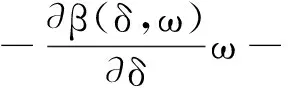
(29)

由式(28)和式(29)可得

(30)

取Lyapunov函数:V3=0.5z2,求导可得

(31)

令

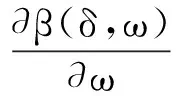
(32)

由式(30)～式(32)可得

(33)

z=c2e-γ1t

(34)

式中:c2与z的初值相关;z呈指数收敛。

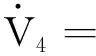
s1{ke1-z-[hs1+ηtanh(s1/σ)]}

(35)

取η>max|z|,c1+λ1>0,h>0,1+k=0,即可保证V4负定,基于浸入与不变原理的自适应反步滑模控制器设计完毕。

3 仿真验证

3.1 I &I-ABSMC的参数分析

由于I &I-ABSMC的不同控制参数会对水轮机调节系统的状态变量收敛以及扰动跟踪的效果产生较大影响,所以进行了控制器参数变化时的对比试验。其中,系统参数的选取参照表1,假设外部扰动d=12cos(0.1t),初始条件(0.001,0.001,0.001,0.001),δd=0。补偿函数的偏导数γ1变化时机械力矩相对偏差的收敛曲线以及扰动跟踪曲线如图2所示,其余控制器参数选取:λ=1,c1=3,h=3,η=2,σ=0.1,λ1=1,k=-1。由图2(a)可以观察出,虽然不同的γ1取值均可以使控制器在有限时间内跟踪到扰动的给定值,但是随着γ1的不断增大,基于浸入与不变原理的自适应反步滑模控制器对扰动跟踪的超调量会明显增加,且扰动的估计值会更慢地收敛到给定值。而且由图2(b)可以分析出,γ1取不同值时机械力矩相对偏差收敛曲线完全重合,即改变γ1的取值不会影响机械力矩相对偏差的收敛状况。

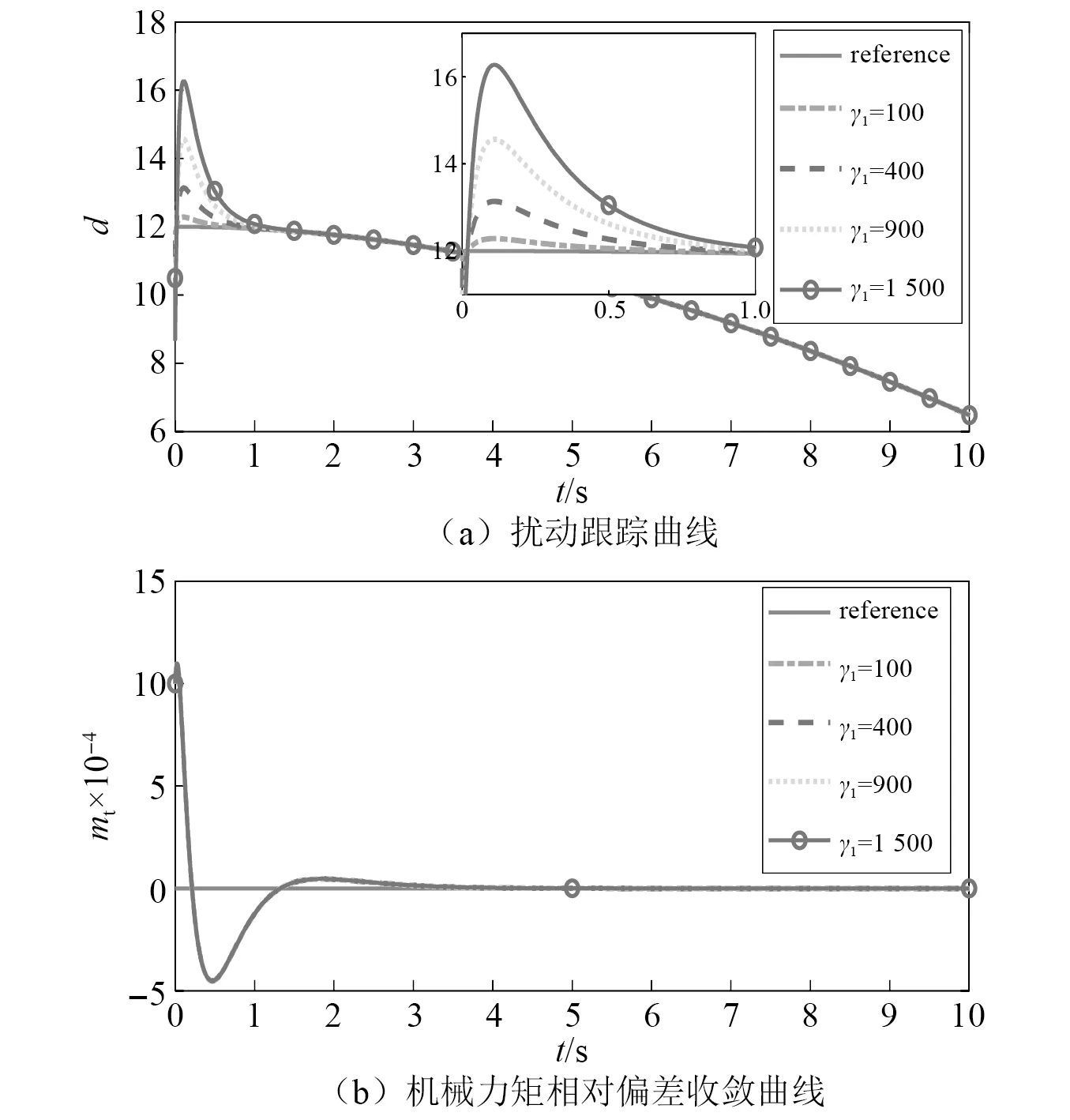
图2 γ1变化时系统的响应曲线Fig.2 Response curve of the system when γ1 changes

控制器中参数σ的选取对水轮机调节系统的响应曲线的影响如图3所示,此时其他控制参数的选取:λ=1,c1=3,h=3,η=2,λ1=1,σ=0.1,γ1=100,k=-1。从图3(a)可知,随着σ的增大,本控制器作用下的水轮机调节系统扰动估计值的超调量有一定的降低,但是在跟踪扰动给定值的速度方面会更慢。由图3(b)可以观察出,更大的σ值会使其机械力矩相对偏差收敛曲线的超调更明显,且收敛速度更慢。

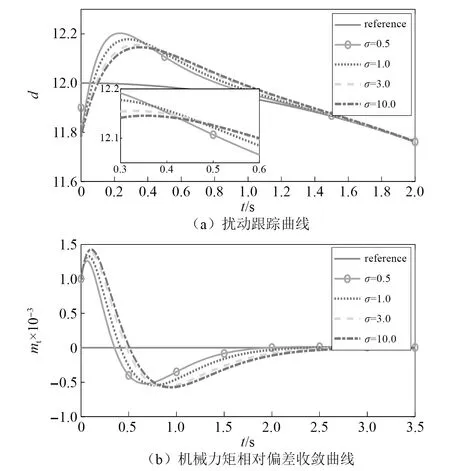
图3 σ变化时系统的响应曲线Fig.3 Response curve of the system when σ changes

由以上分析可知,控制器参数应在合理的范围内选取,γ1和σ取值越小则控制效果越好,为了不失一般性,本控制器取γ1=100,σ=0.1。其他控制参数的分析过程类似,不再赘述。其余控制器参数选取:λ=1,c1=3,h=3,η=2,λ1=1,k=-1。

3.2 不同控制器的控制效果对比

为了验证I &I-ABSMC控制效果,将其与ABSMC和基于非线性干扰观测器的自适应反步滑模控制器(nonlinear disturbance observer-ABSMC,NDO-ABSMC)进行对比试验。

图4给出了两时间尺度水轮机调节系统的状态变量在3种控制器作用下的收敛曲线。由图4可得,上述3种控制器都可以实现水轮机调节系统簇发振荡的抑制。但是,相比于其他2种控制方式,基于浸入与不变原理的自适应反步滑模控制具有收敛时间更短、过渡过程更平滑、状态变量过冲更小的特点。由图4(a)和图4(b)可以分析出,发电机转子角度相对偏差和转速相对偏差在自适应反步滑模控制器的作用下收敛时间最长,过冲明显更大。由图4(c)和图4(d)可以分析出,机械力矩相对偏差和导叶开度相对偏差在非线性干扰观测器作用下的过冲更大,尤其是导叶开度相对偏差的最大过冲接近于其他2种控制方式的30倍且振荡持续整个控制过程,在收敛时间较长时会进一步加剧系统的不稳定。

图4 不同控制器时的状态变量收敛曲线Fig.4 Convergence curves of state variables with different controllers

图5显示了3种控制器对扰动的估计情况,由图5可以分析出,自适应反步滑模控制跟踪扰动的速度明显最慢且初始阶段误差最大。虽然基于浸入与不变原理的自适应反步滑模控制器和基于非线性干扰观测器的反步滑模控制器在跟踪扰动的速度方面相差无几,但前一种控制器的扰动估计值和实际值之间的误差明显更小。

图5 不同控制器时的扰动估计Fig.5 Estimation of disturbance with different controllers

可以看出,引入浸入与不变流形后,系统的簇发振荡现象得到抑制的同时,其状态变量的收敛速度和对外部扰动的适应能力相比于其他两种控制策略都得到了一定的提高。

上述研究仅证明了I &I-ABSMC在系统发生簇发振荡时具有较好的控制效果,为了验证I &I-ABSMC在常规工况下的控制效果,取式(1)刚性水击时的水轮机调节系统模型为被控对象,得到常规工况时系统在3种控制器作用下的状态变量收敛曲线和扰动跟踪效果如图6所示。由图6(a)和图6(b)可知,机组常规工况下的发电机转子角度相对偏差、转速相对偏差在I &I-ABSMC的作用下收敛速度更快、超调量更小。但是在机械力矩相对偏差的收敛速度以及超调量方面,ABSMC表现较好。结合图6(d)和图6(e)的导叶开度相对偏差的收敛情况以及对扰动的跟踪效果,I &I-ABSMC在全状态范围内的表现仍优于其他2种控制策略。

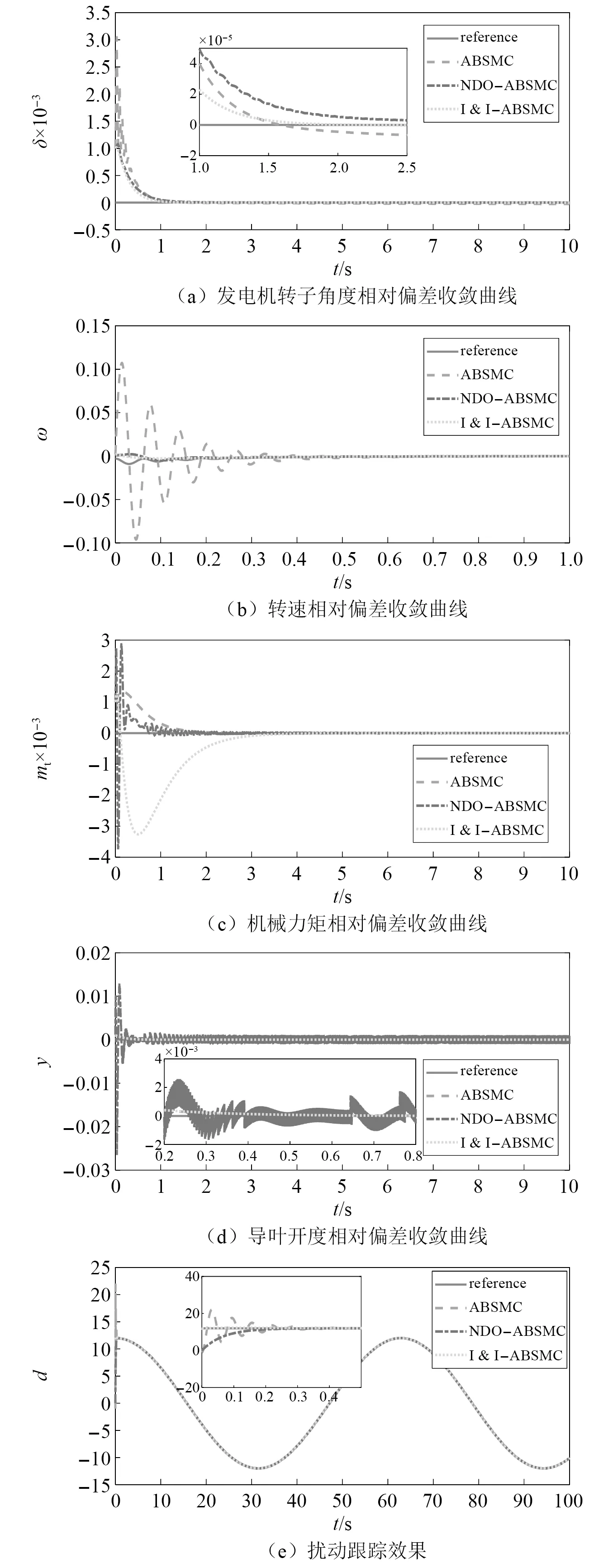
图6 常规工况下的控制效果对比曲线Fig.6 Comparison curve of the control results under normal conditions

当机组在额定工况下运行时,水轮发电机组的功角应该等于电网的功角,即发电机转子角度相对偏差δ=0;速度应该保持在额定速度,即转速相对偏差ω=0;水轮机力矩应保持恒定,以维持水轮机转速的稳定,即水轮机机械力矩相对偏差mt=0;导叶开度为额定开度,即y=0[18]。考虑水轮机调节系统实际运行情况,若运行过程中发生失稳行为会对整个系统造成极大的危害,为了证明本文所提方法对运行过程中失稳行为的控制效果,假定在0.3 s时施加I &I-ABSMC控制器,其状态变量的收敛曲线以及扰动的跟踪效果如图7所示。观察图7(a)～图7(d)可知,加入控制器的瞬间,水轮机调节系统的发电机转子角度相对偏差、转速相对偏差、机械力矩相对偏差、导叶开度相对偏差经历一定的过冲后均会在一定时间内收敛到稳态。由图7(e)可以分析出,扰动的估计值在加入控制器后出现了很大的超调,这与本控制器的控制参数γ1的选取有关,γ1取更小的值将极大的降低超调量。由图7(f)可知,本系统中的基于浸入与不变原理的自适应反步滑模控制器的响应速度较快,控制量可以实现稳定输出。

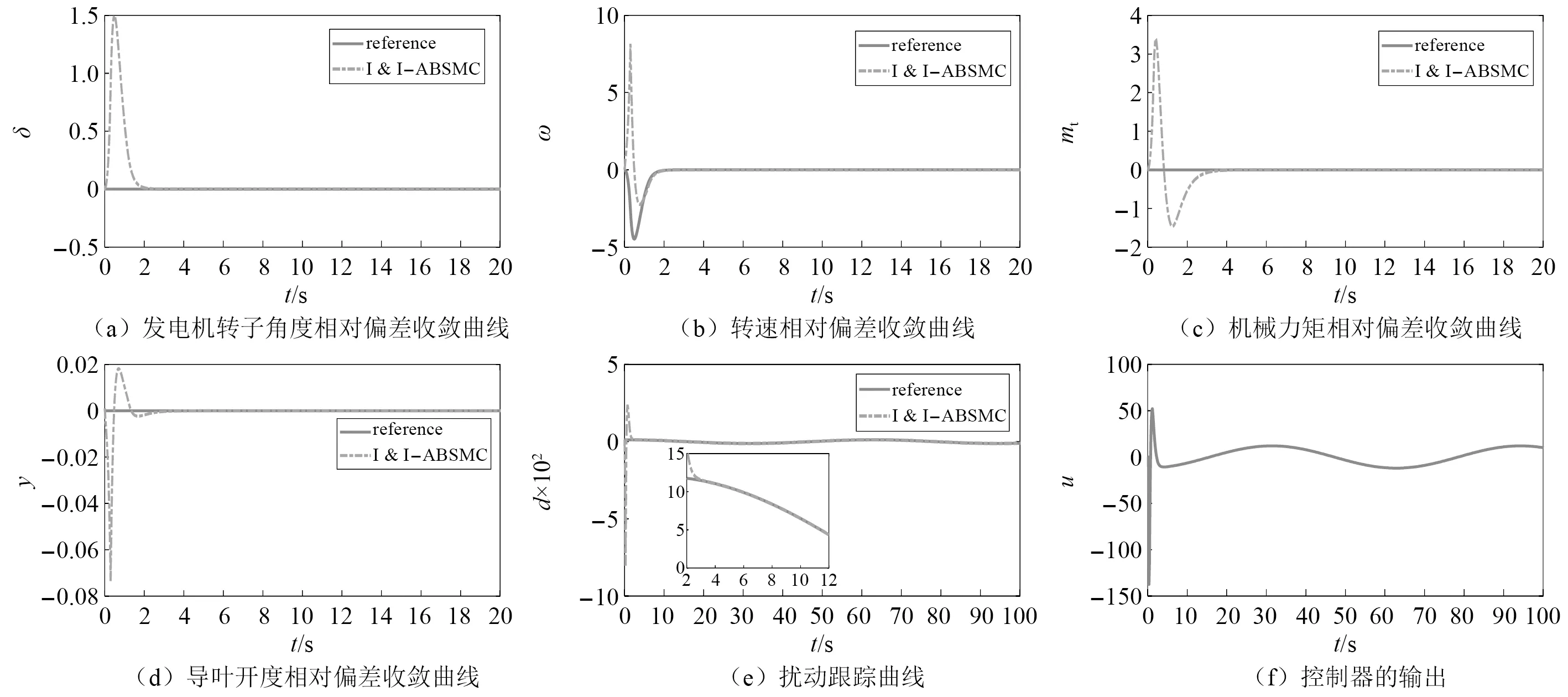
图7 运行过程中加入控制器后的系统响应曲线Fig.7 Response curve of the system after adding controller during operation

上述分析均是在水轮机调节系统于初始时刻即存在扰动的情形下进行的,但是实际中扰动往往是在系统运行过程中突然加入,因此,为了进一步验证控制器的鲁棒性,假设在3 s时施加扰动d,其取值同3.1节。仿真结果如图8所示,综合图8(a)～图8(d)可知,突加扰动后,I &I-ABSMC作用下的水轮机调节系统各状态变量的收敛速度和超调量方面仍然更优,其他两种控制策略在部分状态变量上表现尚可,但是在全状态范围内的表现较差,即具有较差的鲁棒性。由图8(e)可知,I &I-ABSMC以极快的速度跟踪扰动,而NDO-ABSMC跟踪扰动时虽然超调量和I &I-ABSMC几乎一致,但是约0.3 s才实现完全跟踪,速度明显更慢。可以很明显的看出,ABSMC在跟踪扰动时超调量明显更大,且扰动的估计值和实际值约0.4 s才重合。由以上分析可知,突加扰动时I &I-ABSMC依然具有更好的表现。

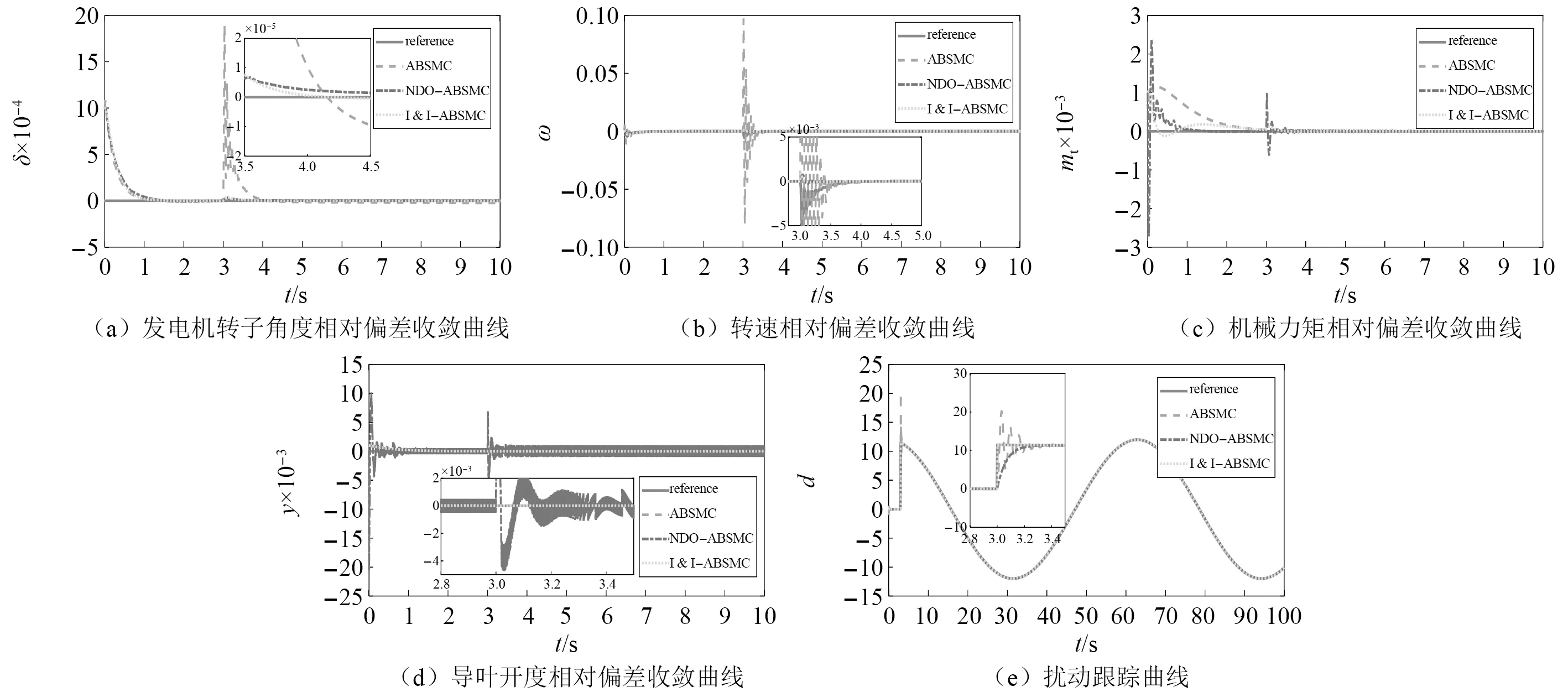
图8 突加扰动的控制效果对比曲线Fig.8 Comparison curve of the control results after sudden disturbance

4 结 论

本文以水轮机调节系统为研究对象,利用两时间尺度四阶水轮机调节系统模型,通过相图和时序图分析了其簇发振荡行为。对于水轮机调节系统的簇发振荡抑制问题,设计了3种基于反步法和滑模理论的控制器进行对比试验。相同条件下的仿真结果表明:在保证水轮机调节系统稳定运行的前提下,相比于自适应反步滑模控制和基于非线性干扰观测器的反步滑模控制,基于浸入与不变原理的自适应反步滑模控制解决了传统方法对扰动的估计不足导致的跟踪性能较差的问题。同时,机组常规工况下的对比试验进一步验证了基于浸入与不变原理的自适应反步滑模控制的通用性。通过进行水轮机调节系统实际运行过程中控制器的延时施加以及扰动的突然加入这两组试验,证明了本控制方法具有较强的鲁棒性。本文所提控制策略亦可以应用到更高阶的水轮机调节系统簇发振荡行为的抑制中。