斜盘式轴向柱塞泵壳体动态特性分析
宋华庆, 王 涛, 汪浒江, 唐守生, 董兴建
(1. 上海交通大学 振动、冲击、噪声研究所, 上海 200240;2. 中国北方车辆研究所 车辆传动重点实验室, 北京 100072)
轴向柱塞泵是液压系统重要的动力元件,广泛应用于工程机械和武器装备等领域中,同时,轴向柱塞泵也是液压系统最主要的振动与噪声源[1],随着液压系统向高速、高压和高功重比方向发展,轴向柱塞泵的振动噪声问题尤其突出[2-3],甚至影响液压系统的整体性能。
轴向柱塞泵噪声包括流体噪声和机械噪声。通过优化轴向柱塞泵内部流道、配流盘和滑靴副的结构参数,从源头上降低轴向柱塞泵工作时的压力冲击和流量脉动是轴向柱塞泵流体噪声控制与治理的重要手段。航空工业第一飞机设计研究院的张辉等[4]采用多块结构化网格策略分析轴向柱塞泵内部流场特征,提出可用于轴向柱塞泵压力冲击分析和流道优化设计的计算方法。Kumar等[5]使用计算流体力学 (computational fluid dynamics ,CFD) 方法研究了轴向柱塞泵滑靴的静态及动态特性,并对滑靴做出了优化设计提高了轴向柱塞泵工作的平稳性。Guan等[6]借助CFD技术建立了带阻尼孔配流盘的轴向柱塞泵流量脉动模型,并给出了控制其流量脉动的设计建议。徐兵等[7]建立用于轴向柱塞泵噪声激振源评估的流量仿真理论模型,提出可通过优化转位角降低轴向柱塞泵出口流量脉动。
通过减小结构对激励的响应从而降低机械噪声是轴向柱塞泵振动噪声治理的另一有效手段。Palmen[8]在分析加强筋结构对频响函数影响的基础上,在轴向柱塞泵壳体内壁加星型加强筋,在不同转速下对轴向柱塞泵的噪声进行测试,发现可以降低噪声1~3 dB。权凌霄等[9]基于振动传递路径分析方法建立了轴向柱塞泵后壳体集中参数模型,通过数值模拟和试验方法确定模型参数,为壳体优化奠定了基础。Manring等[10]在对串联式轴向柱塞泵转矩波动的研究中发现,适当选择转位角可将转矩脉动幅度降低75%。Ye等[11]将轴向柱塞泵建模为具有4个集中质量和19个自由度的动态系统,并通过试验验证了模型的正确性,发现通过优化螺栓安装位置可显著降低轴向柱塞泵的振动噪声。
由前人研究可知,壳体动态特性分析是轴向柱塞泵机械噪声控制的基础。以往的轴向柱塞泵壳体振动分析,或侧重于试验研究,在动力学模型建模方面有所不足,或对壳体的内部激励机理缺乏科学认识。为此,本文采用单向解耦方法对斜盘式轴向柱塞泵壳体加以分析,从泵转子和壳体之间的三大载荷传递路径入手,逐一明确滑靴、轴承和配流盘等运动部件对壳体的动态激励,建立壳体动态特性分析的有限元模型,并对其进行试验验证,最后,基于振动烈度评估壳体结构的振动大小。研究成果为面向减振降噪的斜盘式轴向柱塞泵壳体结构优化设计提供一定的理论依据。
1 “转子-斜盘-壳体”路径中的动态载荷
1.1 柱塞-滑靴组件受力分析
如图1所示,斜盘式轴向柱塞泵可分为壳体结构和转子结构,转子和壳体通过斜盘、配流盘和轴承发生相互作用,从而形成“转子-斜盘-壳体”、“转子-配流盘-壳体”和“转子-轴承-壳体”三大载荷传递路径。对于“转子-斜盘-壳体”这条载荷传递路径,滑靴作用于斜盘的载荷即转子通过斜盘作用于壳体之载荷。
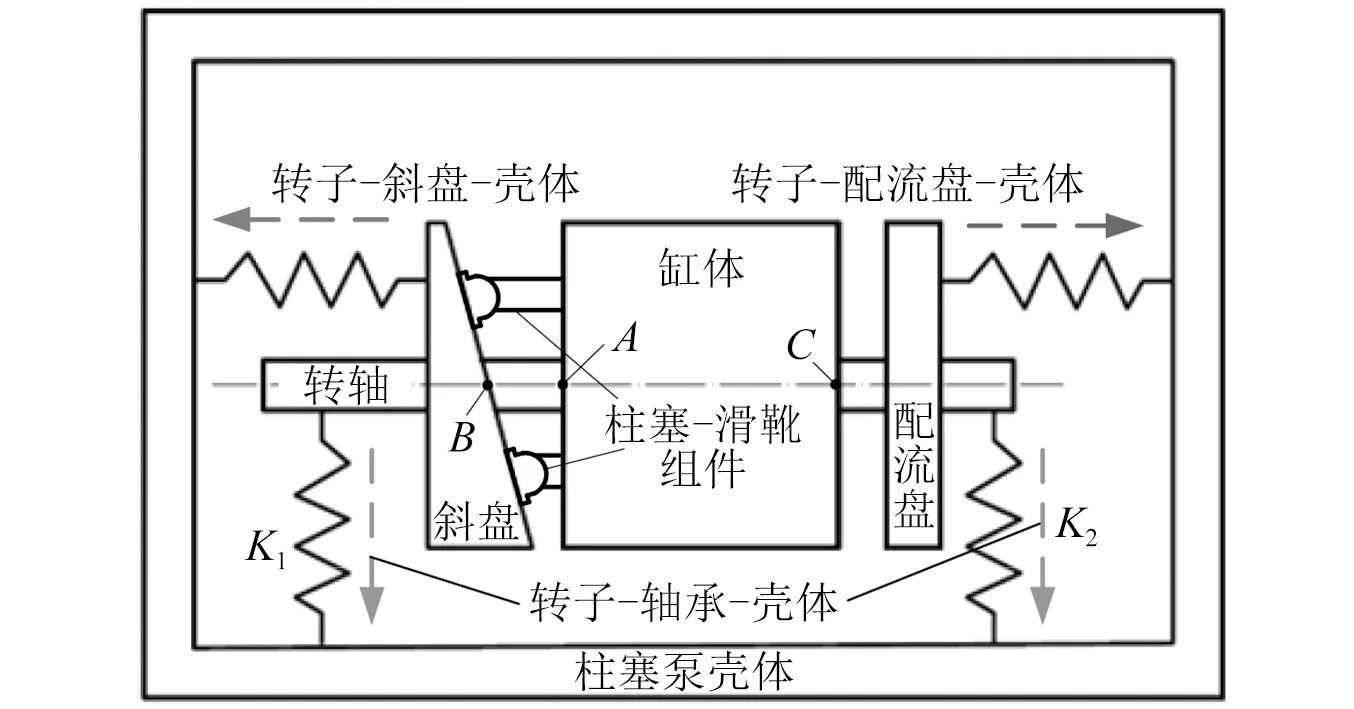
图1 柱塞泵三大载荷传递路径Fig.1 Three load transmission paths of the piston pump
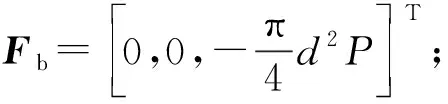
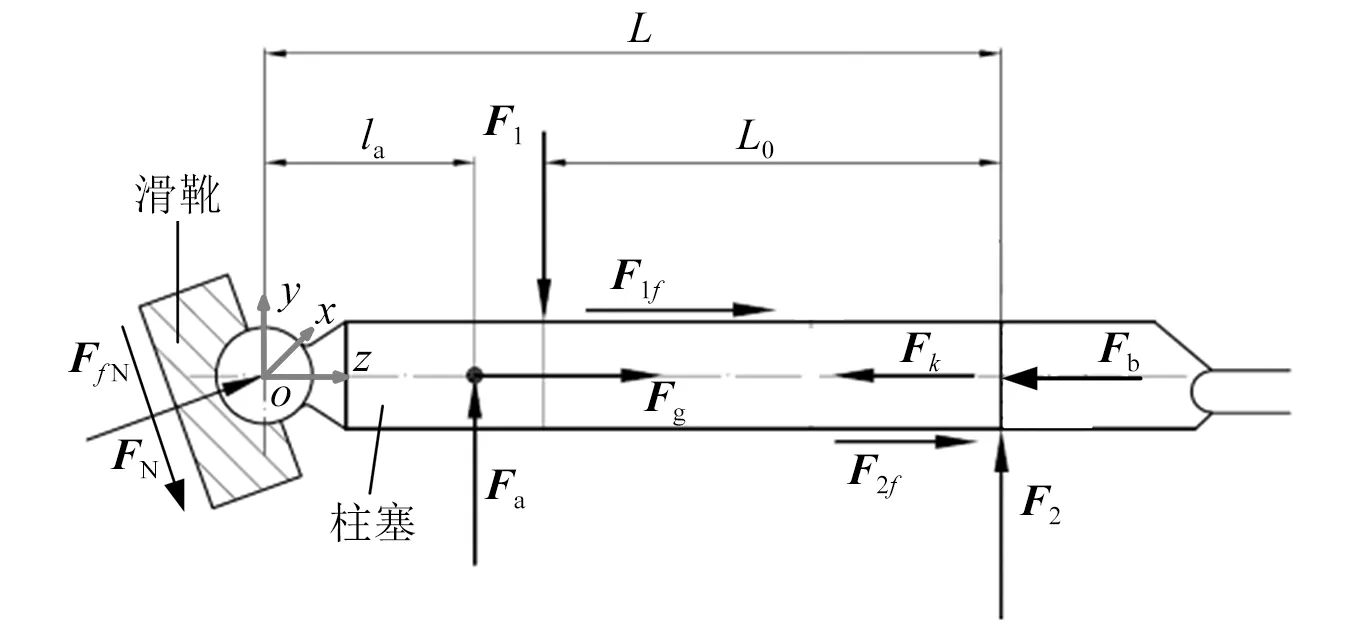
图2 “滑靴-柱塞”组件受力简图Fig.2 Schematic of the load of the piston-slipper system
1.2 柱塞-滑靴组件的动态平衡方程
在柱塞-滑靴组件运动过程中,将柱塞-滑靴组件所受各力投影至坐标轴上,建立力和力矩的动态平衡方程。
(1)
(2)
式中:L为柱塞长度;la为柱塞-滑靴质心到柱塞球头中心的距离;l0为柱塞在柱塞腔内长度;f1和f2分别为滑靴与斜盘间摩擦因数和柱塞与柱塞腔壁之间摩擦因数。
以上死点为起点,规定此时转角为零。当转角处于[0, π]时,柱塞处于高压区,此时P=PH,柱塞进行压油动作;当转角处于(π, 2π]时,柱塞处于低压区,此时P=PL,柱塞进行吸油动作。
表1所示为求解平衡方程所需轴向柱塞泵参数,联立式(1)、式(2),求解得到轴向柱塞泵在不同工作压力下斜盘对滑靴支承力FN如图3、图4所示。

表1 轴向柱塞泵参数表Tab.1 The parameter of the axial piston pump

图3 不同压力下斜盘对滑靴支承力(ω=2 100 r/min)Fig.3 Supporting force of swashplate to slipper under different pressures(ω=2 100 r/min)

图4 不同转速下斜盘对滑靴支承力(PH=40 MPa)Fig.4 Supporting force of swashplate to slipper under different speed(PH=40 MPa)
对比变压力和变转速下斜盘对滑靴支承力FN的结果,可以明显看出压力对支承力的影响远大于转速对支承力的影响。其原因在于:相对于液压载荷,惯性力对滑靴支承力FN的影响可忽略不计。
1.3 转子对斜盘的载荷
定义轴向柱塞泵缸体斜盘侧端面中心为点A(见图1),单个柱塞-滑靴组件对斜盘的作用力为Fsi,其为斜盘对滑靴支承力FN及摩擦力FfN合力的反力,Fsi作用点到A点的矢径为rsi。将9个柱塞-滑靴组件对斜盘的作用力全部简化至A点,简化后所得主矢和主矩,即为转子对斜盘的载荷。
(3)
(4)
rsi=[Rsinθi,-Rcosθi,Ldis+Rtanγcosθi]T
(5)
式中:Fs为简化后主矢;Ms为简化后主矩;Ldis=30 mm为轴向柱塞泵缸体端面中心距斜盘中心的距离,即图1中AB。
2 “转子-配流盘-壳体”路径中的动态载荷
当轴向柱塞泵工作时,配流副的间隙中充满了液压油,轴向柱塞泵缸体通过间隙中的液压油对配流盘的液压推力即是“转子-配流盘-壳体”路径中转子通过配流盘作用于壳体之载荷。
假设配流盘边界油液压力为0,配流副间隙中油液压力为对数分布,得配流盘所受油液推力。
(6)
式中:Pb为配流盘腰型槽内压力;R1为内密封带边界;R2为配流盘腰型槽小径;R3为配流盘腰型槽大径;R4为外密封带边界;Φ为配流盘上压力包角(参数见图5与表2)。

表2 配流盘参数表Tab.2 The parameter of the valve-plate

图5 配流盘压力分布Fig.5 The pressure distribution of the valve-plate
由式(6)可知,当配流盘结构确定后,影响配流盘推力Fp大小的因素包括压力包角Φ和腰型槽内压力Pb,其中在压油区Pb=PH,在吸油区Pb=PL。配流盘的压力分布如图5所示。
如图1所示,定义缸体配流盘侧端面中心为点C,由文献[12]可以计算得到压油区和吸油区的配流盘推力作用位置,其到C点的矢径分别为rH,rL,将缸体对配流盘的作用力简化至C点,简化后所得主矢和主矩,即为转子对配流盘的载荷。
Fgap=Fgap_H+Fgap_L
(7)
Mgap=rH×Fgap_H+rL×Fgap_L
(8)
式中:Fgap与Mgap分别为简化后主矢与主矩;Fgap_H与Fgap_L分别为吸油区和压油区配流盘所受油液推力。
将表2中参数代入式(6)计算得到配流盘推力,如图6所示。可以看出Fgap_H与Fgap_L在转轴旋转一周的过程中呈现9次周期变化,这是由于9个柱塞腔的存在使得压力包角出现周期变化。
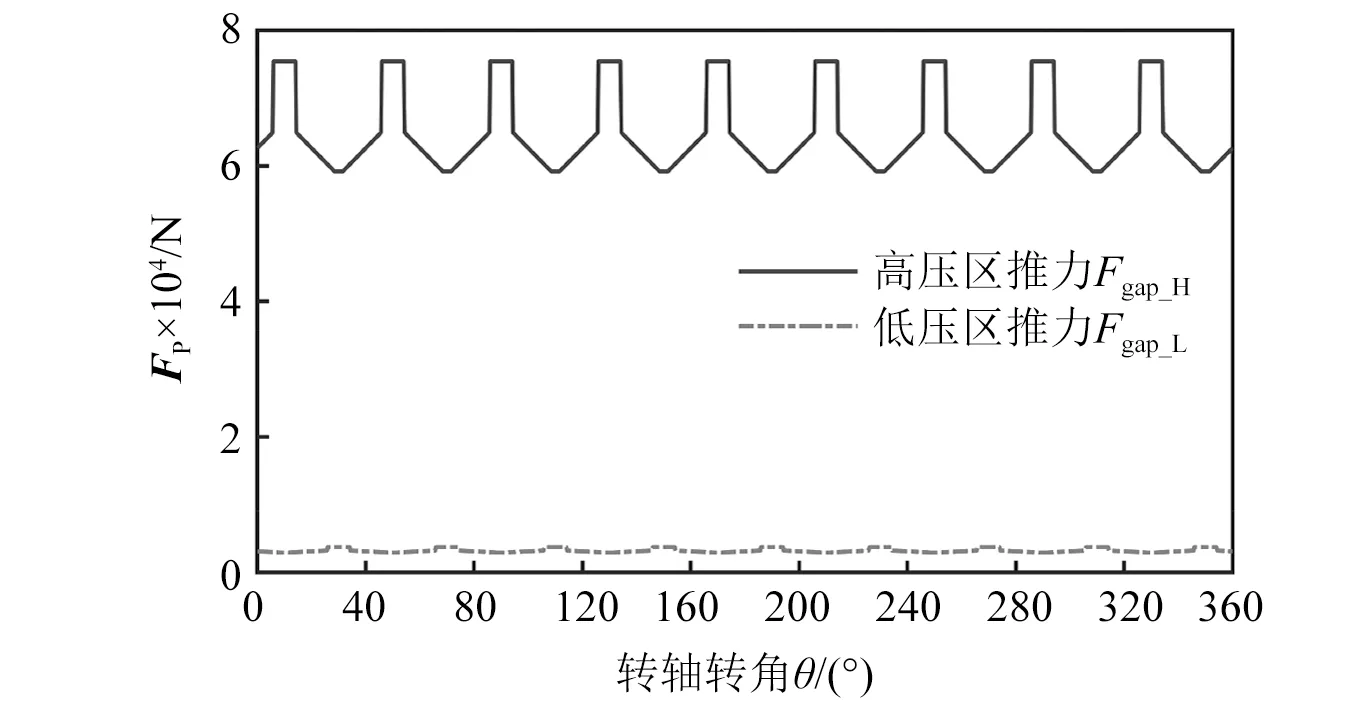
图6 配流盘所受油液推力(PH=40 MPa, PL=2 MPa)Fig.6 The hydraulic thrust of valve-plate(PH=40 MPa, PL=2 MPa)
3 “转子-轴承-壳体”路径中的动态载荷
如图1所示,轴向柱塞泵转子包括转轴、柱塞-滑靴组件和缸体,支撑在前轴承k1和尾轴承k2上,受到斜盘和配流盘的激励作用。“转子-轴承-壳体”路径中的动态载荷即为转子通过轴承作用于壳体之载荷。滚动轴承在工作时由于滚动体和内外圈的相对位置变化使其支承刚度发生改变,借助滚动轴承分析理论[13-14]以及虚滚子假设[15],可以计算得到滚动轴承的时变支承刚度,前轴承及尾轴承的时变刚度如图7 所示。将转轴和缸体视为同一部件,使用梁单元建模,柱塞-滑靴组件使用集中质量单元建模,支承轴承采用弹簧建模,建立如图8所示的轴向柱塞泵转子有限元模型。
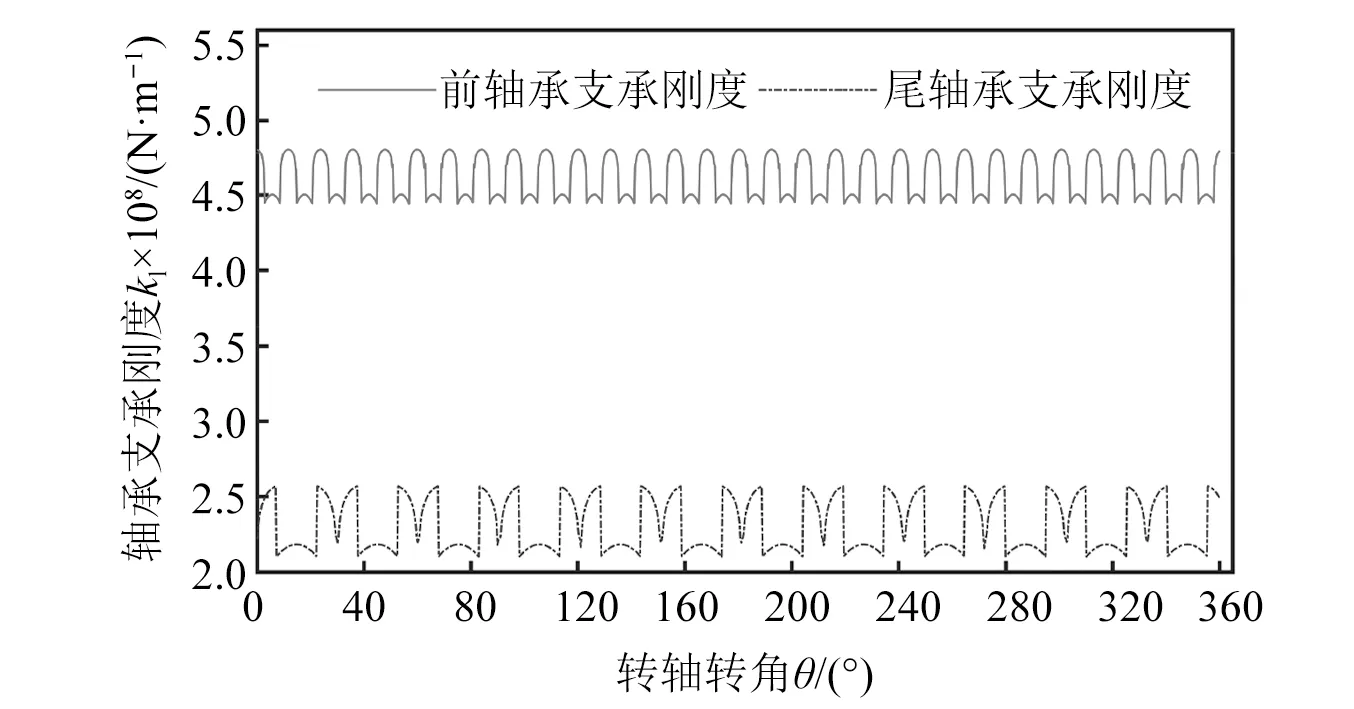
图7 轴承支承刚度曲线Fig.7 The bearing stiffness curve
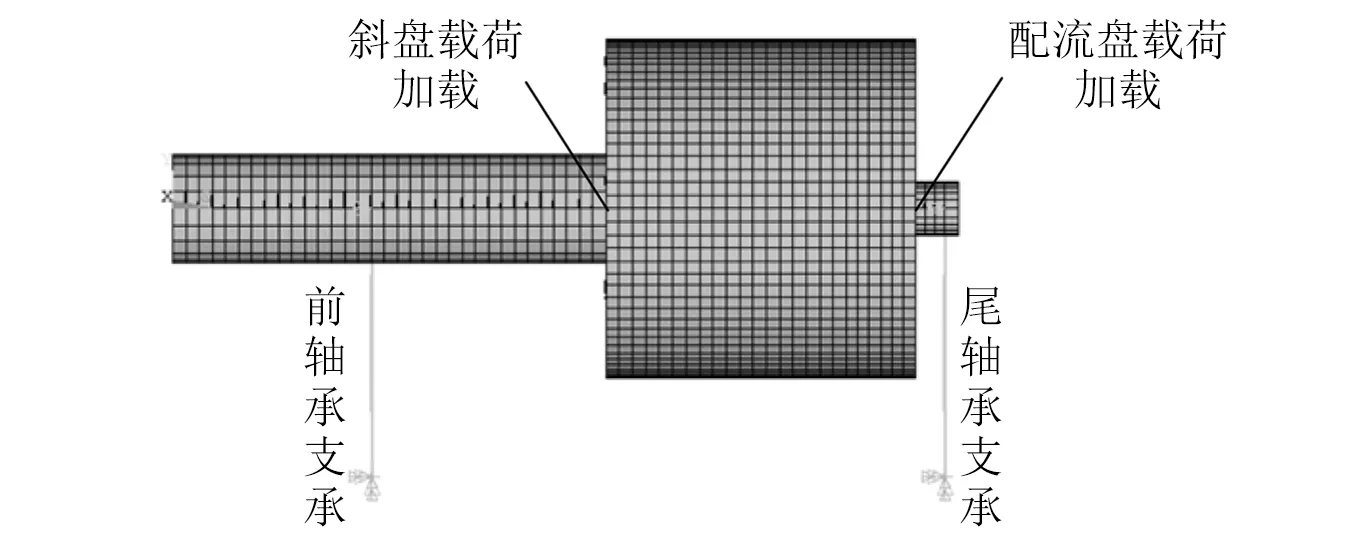
图8 轴向柱塞泵转子有限元模型Fig.8 The finite element model of the axial piston pump rotor
结合所得转子轴承支承刚度和外载荷激励,借助ANSYS使用完全法对轴向柱塞泵转子做瞬态动力学仿真,提取得到转子两个轴承的支承力如图9所示。轴承支承力对应的反作用力即为柱塞泵转子经轴承对柱塞泵壳体作用的载荷。
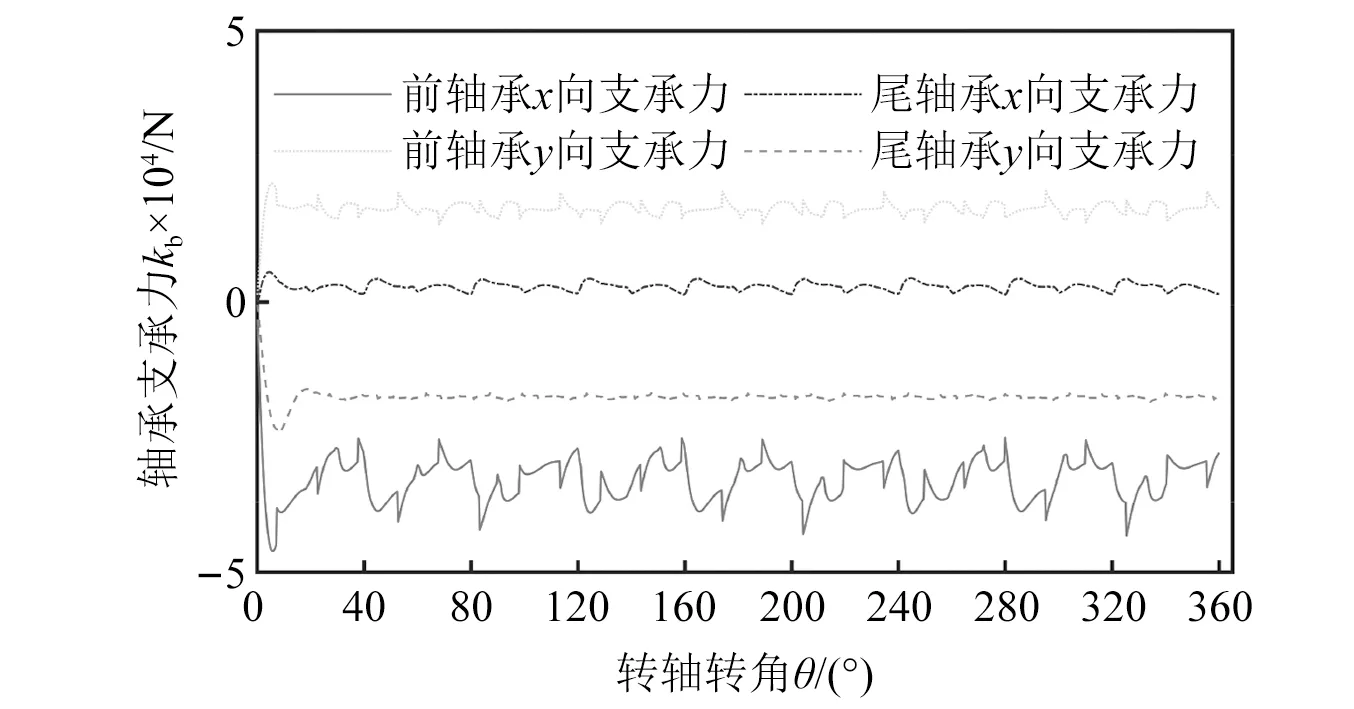
图9 轴承支承力(3 500 r/min, 40 MPa)Fig.9 The bearing supporting force(3 500 r/min, 40 MPa)
4 壳体振动响应计算与分析
4.1 轴向柱塞泵壳体仿真模型
轴向柱塞泵壳体几何模型如图10所示,由端盖、主壳体和流道三部分装配而成,使用Solid185实体单元对其进行有限元网格划分。实际结构中,壳体各部件之间由螺栓连接,刚度较大,因此在有限元模型中使用节点绑定连接装配面进行等效。
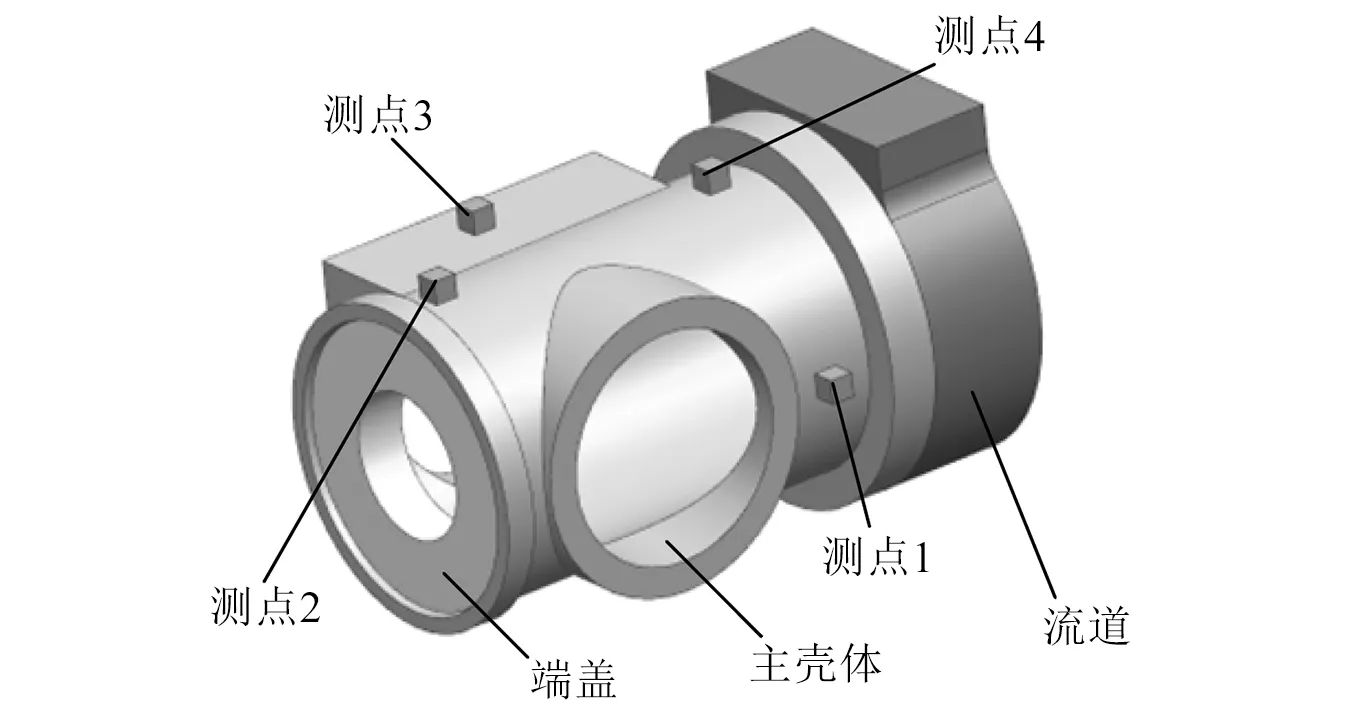
图10 柱塞泵壳体几何模型及振动测点布置Fig.10 The geometric model of piston pump housing and vibration measuring points arrangement
为验证壳体有限元模型的正确性,使用模态、振动、噪声测试分析系统LMS对壳体进行模态测试试验(如图11所示),对比壳体自由模态的试验和仿真结果如表3所示。
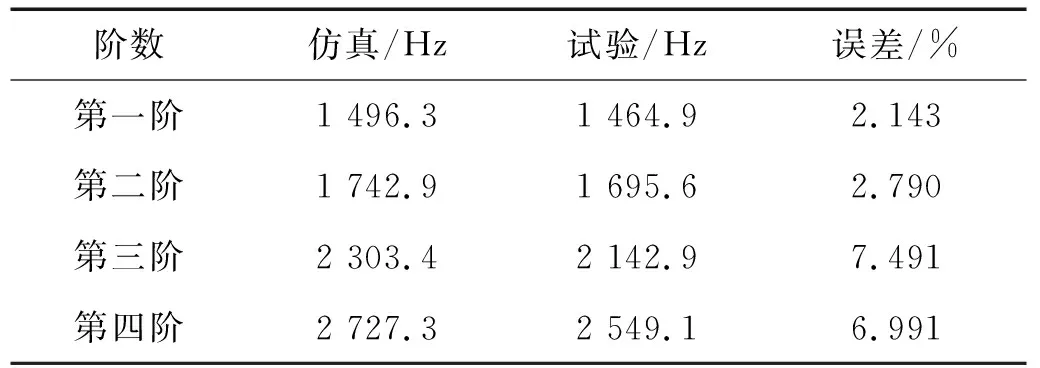
表3 柱塞泵壳体固有频率Tab.3 The natural frequency of the piston pump housing

图11 柱塞泵壳体模态试验Fig.11 The modal test of the piston pump housing
从表3可以看出,壳体自由模态的仿真结果和试验测试结果接近,二者之间误差在可接受范围之内,故可认为所建立的柱塞泵壳体仿真模型是可信的。
4.2 壳体稳态响应分析及试验验证
在对轴向柱塞泵壳体进行仿真计算过程中,使用前述三条载荷传递路径所传递载荷代替轴向柱塞泵转子和壳体结构之间的相互作用,即可实现柱塞泵转子结构和壳体结构之间的单向解耦。采用模态叠加法计算稳态工况下的壳体振动响应,并通过柱塞泵壳体振动响应试验验证。搭建如图12所示的试验平台,通过东华DH8303N动态信号分析仪完成采集与分析,其中加速度传感器通过磁性座安装在壳体上(见图11)。试验壳体测点布置方案见图10,设定采样频率为50 kHz,在不同工况下采集柱塞泵壳体的加速度数据。

图12 柱塞泵壳体振动响应试验台Fig12 The experiment plateform for vibration response of piston pump housing
得到柱塞泵壳体测点1试验与仿真频域响应结果对比如图13所示。可以看出,仿真得到的轴向柱塞泵壳体加速度响应频谱与试验测试结果基本一致。进一步分析图示频谱成分,可以看出,泵壳体振动加速度的峰值频率均出现在525 Hz的倍频点附近。这是由于在转速ω=3 500 r/min时,转子转频为58.33 Hz,同时柱塞泵缸体上均布有9个柱塞腔,使得柱塞泵壳体上激励频率的基频是转子转频的9倍,即525 Hz。

图13 测点1加速度响应(3 500 r/min, 40 MPa)Fig.13 The acceleration response of measuring point 1(3 500 r/min, 40 MPa)
进一步地,使用振动烈度评估柱塞泵壳体振动,分析各个稳态工况下壳体的振动程度。振动烈度可由式(9)计算[16]
(9)
式中:Vx,Vy,Vz分别为测点位置x,y,z3个方向上速度的有效值;N为测点个数。得到柱塞泵壳体的振动烈度如图14所示。

图14 壳体振动烈度Fig.14 The vibration intensity of piston pump housing
由图14可知,轴向柱塞泵工作转速和工作压力均对壳体的振动烈度有重要的影响。结合式(6)与图3、图4和图14可知,相对于工作压力,转子转速的变化对于载荷影响极小,而就壳体振动烈度结果而言,同样工作压力下,转速的上升会使得柱塞泵壳体的振动烈度明显提升,造成这一结果的主要原因是在外激励频率低于壳体一阶固有频率,此时在激励幅值接近的情况下,转子转速的上升使得激励频率增大,从而使得壳体振动烈度加剧。
5 结 论
鉴于轴向柱塞泵结构的复杂性,本文提出单向解耦的方法分析柱塞泵的载荷传递路径,并对壳体的动态特性进行研究,同时分析壳体的振动烈度,得到如下结论:
(1) 单向解耦方法是研究柱塞泵壳体动态特性的有效手段。本文以分析力学为基础,采用单向解耦方法建立了轴向柱塞泵的数学模型,能将复杂的斜盘式轴向柱塞泵系统简化,同时完整反映泵壳体的振动特性。
(2) 采用理论仿真与试验方法对柱塞泵壳体振动响应进行分析,所得理论分析结果与试验相符,模型精度较高。表明单向解耦方法能很好的揭示轴向柱塞泵内部载荷传递规律,这可为柱塞泵的振动传递路径分析以及减振降噪提供一定的理论依据。
(3)轴向柱塞泵的工作转速与工作压力均会影响其壳体的振动烈度。其中压力通过影响载荷幅值影响壳体振动烈度,而转速通过影响载荷频率影响壳体振动烈度。
(4)壳体的动态特性分析能够为轴向柱塞泵的减振降噪提供指导。不同稳态工况下轴向柱塞泵壳体的振动烈度分析结果为斜盘式轴向柱塞泵壳体进一步的拓扑优化设计奠定了理论基础。

