借助图形理解圆的外切、内接正方形之间的面积关系
2023-09-01 08:33文|程晨
小学教学设计(数学) 2023年8期
文|程 晨
圆的外切、内接正方形是六年级学生学习圆与正方形面积关系的难点。如何有效掌握重点,突破难点,可采用以下的教学过程。
一、基础入手,探究圆与正方形面积之间的关系
1.读懂题意,尝试解决
两个圆的半径都是1m,“外方内圆”中,正方形面积与圆面积的比是多少?“外圆内方”中,圆面积和正方形面积的比是多少?让学生看懂条件和问题后,独立尝试解决,教师巡视。
2.呈现作品,反馈交流
预设学生的答案:
外方内圆:2×2=4(m2)
外圆内方:求正方形面积会有困难,引导添辅助线,将其分解成三角形。
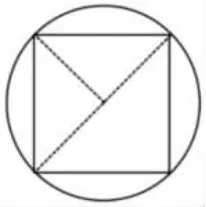
3.更换数据,寻找定律
思考:半径改为2m,3m,4m 或rm,它们间的比会不会变?四人小组,每人选一个数,计算正方形和圆面积的比,组内观察结果,说一说有什么发现。学生发现规律:不管半径是几,“外方内圆”中,正方形面积和圆面积的比始终是4∶π;“外圆内方”中,圆面积和正方形面积比是π∶2。
二、拓展提升,巧算两个图形之间的倍数关系
1.呈现题目,尝试解决
将两图合并呈现后提问:大正方形面积是小正方形面积的几倍?学生独立完成,教师巡视,选择典型方法。
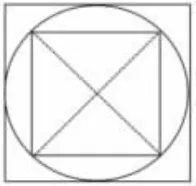
2.呈现作品,反馈交流
预设方法1:设半径为1,大正方形面积为2×2=4(m2),小正方形面积为,大正方形面积是小正方形面积的2 倍。
预设方法2:设半径为r,大正方形面积为2r×2r=4r2(m2),小正方形面积为,大正方形面积是小正方形面积的2 倍。
预设方法3:运用结论“外方内圆”中正方形面积和圆面积的比是4∶π;“外圆内方”中圆面积和正方形面积比是π∶2,推导出两个正方形的面积比是4∶2,大正方形面积是小正方形的2 倍。
3.提供学具,拓宽思路
思考:有没有更简便的办法能直接看出它们是2 倍关系?教师出示学具:用硬卡纸剪出两个正方形和一个圆,用图钉固定好中心且能转动。让学生动手操作,寻找其中的奥秘。发现将小正方形顺时针旋转45°后,能直接看出大正方形面积是小正方形面积的2 倍,如图所示。
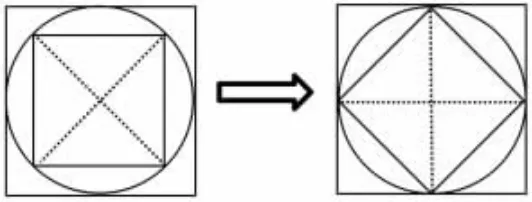
猜你喜欢
中等数学(2022年1期)2022-06-05
福建基础教育研究(2019年8期)2019-05-28
中等数学(2018年4期)2018-08-01
中学数学研究(广东)(2018年23期)2018-03-05
初中生世界·九年级(2017年9期)2017-10-13
数学学习与研究(2017年3期)2017-03-09
中学数学杂志(初中版)(2016年5期)2016-11-01
中国教育技术装备(2015年21期)2015-03-11
读写算(下)(2015年10期)2015-01-03
现代教育科研论坛(2009年7期)2009-10-15

