整体设计 寻求“通法” 关联本质
——『小数乘除法的复习』教学实践与思考
文 庄丽君
小数乘法、除法运算类型不同,但算法相通,学法相近。复习时沟通两个板块的算法、学法,系统整理其中的计算方法和计算道理,有利于学生从整体上把握知识结构,形成转化思想,感受计算的一致性,发展学生的数学思维。
一、课前思考
“小数乘除法的复习”是人教版五年级上册第一单元“小数乘法”、第三单元“小数除法”的教学内容。按常见教材编排方式,往往是一单元一复习,教材却打破常规,将两个单元放在一起复习,这样编排,绝不是单纯的量的累积。那么,这两个单元内容之间有着怎样的联系?又该如何组织教学展开复习,帮助学生理清联系和建构知识呢?
1.抓住小数乘法与小数除法算法相通之处,体现知识结构的整体性。
横向对比“小数乘法”和“小数除法”两个单元,两者学习内容显然不同,但它们的算法和学法都有相通之处,都是转化成整数乘除法来进行计算,再运用乘除法的运算规律处理积或商的小数点位置。
复习时,可以有意识地抓住这一相通之处做文章,合理选用素材,设计题组练习,整体推进教学。教材以9 道一般的小数乘除法习题为素材,要求学生先计算,再给出整理要点对知识进行梳理。我们对习题素材加以改变,以题组方式呈现,如326×14 和3.26×1.4,798÷57 和7.98÷0.57,这样的题组对比性很强,练习指向明确,学生通过观察、计算,能主动发现题组的数据特点,快速捕捉到小数乘法与除法在算法上的共性———“转化”,从而引导学生整体系统地整理小数乘除法的计算内容,总结转化的数学思想方法,使知识和思想方法都得以结构化。
2.沟通整数乘除法与小数乘除法的内在联系,体会运算本质的一致性。
纵向思考整数乘除法和小数乘除法的关系,前者为后者算理算法的迁移学习提供了重要基础,后者是前者的延伸和拓展。从整数运算到小数运算,仅仅是数范畴的变化吗?在这个过程中,计数单位进行了扩充,运算意义也得以拓展。这时,如果能抓住这一关键联接点有效设计教学,学生就能从根本上体会到乘除法运算的本质就是计数单位的叠加和细分。
其实,从整数乘除法跨越到小数乘除法,很多变化学生是有直观感受的。比如低年级时,10÷3=3……1,学生对有余数的除法已经熟练掌握,学习小数除法后,原来不能再除的可以继续除下去了,原来得数是3……1,现在变成了3.3˙,这是一个非常直观的视觉冲击。有这样的变化其根本原因为何?因为数的领域从整数扩展到了小数,计数单位进行了扩充,1 个一就可以继续细分转化为10个十分之一,计数单位化小,个数增多,得以实现再一次的平均分,所以表象看似不同,但本质指向一致。抓住这一关键变化,恰恰是打通整数除法与小数除法知识脉络,让学生体会运算本质的一致性的绝佳时机。教学时,可以设计一个开放式的问题,启迪学生深度思考——在小数乘除法的学习中,有没有一个算式让你觉得与整数乘除法比有很大差异的、很特别的或是有困惑的?让学生写一写、说一说,抓住源于学生的重要素材,暴露来自学生的真实感受,通过辨析讨论,深度挖掘表象背后的根本原因,直击数学本质。
二、教学实践
(一)巧设计,找共性,梳理知识结构,感悟转化思想
1.对比练习,梳理知识。
学生完成题组练习:326×14,3.26×1.4,798÷57,7.98÷0.57。
(1)反馈普通笔算方法,校对答案。
(2)反馈利用推算得出得数的方法,引发思考。
师:(选取学生作品展示)观察这位同学的做法,你想说什么?
生:他先笔算第一题乘法,第二题不用笔算,只要添小数点就行了。第三题算完后,第四题也是这样处理。
师:看来小数乘除法与整数乘除法之间有着紧密联系。接下去小组合作理一理:小数乘法、除法分别是怎样计算的?它们与整数乘法、除法有什么相同点和不同点呢?
小组交流,全班汇报,师生一起梳理小数乘除法的计算法则。
2.启迪思考,沟通联系。
师:明明是小数乘除法,为什么可以想成整数乘除法去算呢?
生:我们学过积的变化规律,知道因数如果扩大或缩小,积也会跟着扩大或缩小相同的倍数。把3.26×1.4 想成326×14,积就扩大了1000 倍,所以算出得数后,要缩小到原来的
生:小数除法是根据商不变性质,被除数和除数同时扩大或缩小相同的倍数,商不变。所以7.98÷0.57 想成798÷57,商是一样的。
小结:我们在学习小数乘除法时,都是想到了把它们转化成学过的知识,分别依据积的变化规律、商不变的性质转化成整数乘除法去算,同时我们还运用这些规律来处理得数小数点的位置。
【思考:笔算习题以题组方式呈现,学生能快速捕捉到数据特点,但碍于日常做题习惯,大部分学生会题题笔算,但个别学生就会“偷个懒”,第二、四题会省略笔算过程。教学时抓住这样的作品,让学生对比观察,有学生表示自己笔算时其实也是这样思考的,有学生会质疑这样答题“格式”不对,正是这样的强烈对比和矛盾冲突才更能直接切中主题,使学生快速地将思考火力集中到“小数乘法、除法分别是怎样计算的?为什么可以这样算?”并能够从整体的视角对两个单元的计算内容进行结构化的梳理和总结。】
(二)引深思,抓特性,分析背后原因,凸显运算本质
1.提出要求。
师:在小数乘除法的学习中,有没有一个算式让你觉得与整数乘除法有很大差异的、很特别的或是有困惑的?写一写,并说一说你的想法。
2.分组呈现作品,学生介绍想法。
生1:3÷8=0.375,原来3÷8 不够除了,学了小数乘除法后,较小的数也可以除以较大的数了。
生2:10÷3=3.3˙,整数乘除法中除后有余数,学了小数乘除法后余数可以继续除,商还可以是循环小数。
师:10÷3=3……1,余数1 其实和3÷8 一样,原来在整数除法中不够除了,但学了小数除法后,还能继续除。这是为什么?
生:个位上余下的1 可以化成10 个十分之一继续除,如果还有余数再化为几个百分之一继续除,可以不断除下去,结果可能是有限小数,也可能是无限小数。
小结:小数除法和整数除法一样,都是把计数单位不断地转化、细分。
生1:9×0.1=0.9,整数乘法中,积常常越乘越大,小数乘法却越乘越小。
生2:8÷0.1=80,小数除法却相反,以前商越除越小,现在商越除越大。
师:你能说说这背后的原因或藏着的规律吗?
生:一个数(0 除外)乘比1 小的数,积比原数小,乘比1 大的数,积比原数大;一个数除以比1小的数(0 除外),商比原数大……
小结:小数乘除法有着自己的运算规律和特点。
生:4.2÷0.25,可以用商不变性质变成(4.2×4)÷(0.25×4),转化成除数是1 的除法算式,这样方便计算。
小结:利用小数乘除法与整数乘除法的联系,有时也能帮助我们巧算速算。
【思考:要求学生写一个小数乘除法与整数乘除法相比有较大差异的算式,由于问题有一定的自主性和开放性,学生很乐于表达,呈现的素材丰富而又真实,也正因为是自己所写,反馈时,学生说和听的兴趣都很浓厚。不同的算式分组反馈,可以对两个单元中有关运算意义、运算规律、简便运算等知识进行有条理的回顾和梳理,达到复习的效果。其中第一组算式是深刻理解运算本质一致性的重要素材,可以重点反馈,抓住学生“从整数除法中算到个位就结束,到小数除法中可以继续除”的直观感受,深究其中缘由,通过回顾学习过程,深度辨析讨论,感受计数单位的扩充连带着运算意义的拓展,使学生能站在乘除法计算大领域的高度去重新审读这些知识,把前后关联的两块计算内容融为一体,初步体会数与运算的一致性。】
(三)优算法,重推理,培养运算能力,发展数学思维
作为计算类复习课,练习设计除了关注学生知识、技能的掌握度,更要关注学生运算能力的提升和数学思维的发展。
课中设计了这样一组习题:
【思考:练习要求为“计算”,而不是明确要求“用竖式计算”“能简便的要简便”。这样设计,一方面是考查笔算的掌握度;另一方面希望在算法上不限制学生,考查计算方法的灵活性。】
比如6÷0.25,学生出现了两种方法:
方法1:
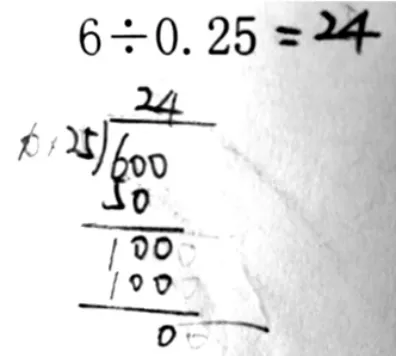
方法2:

两种方法都能得出结果,但思维水平却不同,前者是常规笔算,后者却能自觉运用性质进行简算。
再比如最后一题,学生方法不尽相同,但都想到了运用“转化”的思想方法。
方法1:
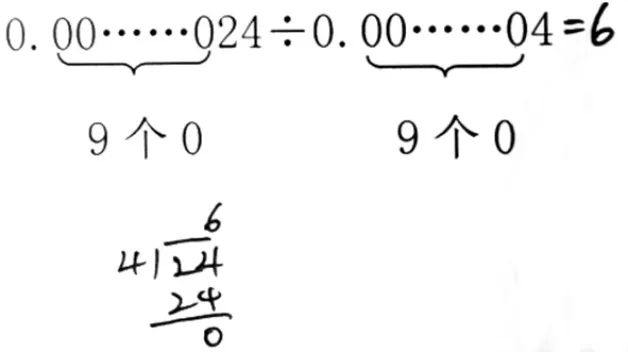
方法2:
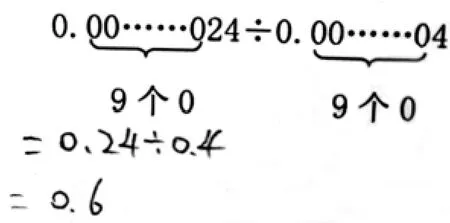
两种方法各有近半数学生,但在计算方法的深刻性上呈现出了一定差异。方法2 更善于从繁杂的表面现象中,抓住事物的本质和核心———即“将除数是小数的除法转化成除数是整数的除法”,并能正确移动小数点得出正确结果。
整节课将两个单元的复习内容合二为一,复习的量看似增加,但基于整合的视角巧妙地设计教学活动,突出复习重点,深化复习目标,更整体地沟通小数乘除法与整数乘除法的内在联系,使学生建立系统的知识结构;更鲜明地体现将未知转化为已知的学习过程,使学生形成转化的思想方法;更深刻地感悟乘除法的本质是计数单位的叠加和细分,使学生体会运算本质的一致性。
——例谈“体积、容积单位换算”教学

