基于计数单位感悟运算一致性
——《分数除以整数》素养进阶习题展评与教学建议
文|鲍莉丽
一、习题展评
●习题一
1.习题内容
算一算,想一想这么算的道理是什么,连一连。
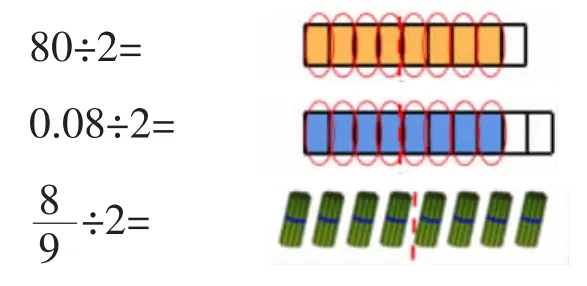
结合算的过程,它们都可以转化为()÷()来计算。
2.能力指向
主要指向运算能力和推理意识。本题的运算能力表现为以下两点:一是如何算,即对算法与运算程序的运用,表现为运算的熟练性;二是“为什么可以这么算”,即对算理的理解。而推理意识表现为对运算一致性的理解,基于计数单位合乎逻辑地运用运算的定义及算理感悟到都是把计数单位的个数平均分。
3.学情分析
本题的正确率达到82.5%,大部分学生能发现这三道计算题都能转化为“8÷2”来计算。说明学生对计算都比较熟练,而且知道计算道理,并能感悟到整数除法、小数除法和分数除以整数之间的运算一致性。
●习题二
1.习题内容


2.能力指向
主要指向运算能力和推理意识。表现为对算法算理的理解,能够根据运算律、运算法则和运算程序进行运算和推理,并理解运算对象、运算律与算法之间的关系,感悟运算的一致性。本题考查分数除以整数,通过对算法算理的理解,发现当分子能被整数整除和不能被整除两种情况都能够从计数单位角度进行分析,感悟把计数单位个数平均分和计数单位平均分的一致性。
3.学情分析
对于分子除以整数,多数学生能通过文字、图示、算式表述出是把计数单位的个数平均分的算理。但是对于分子不能被整数整除的,学生对于平均分计数单位的个数遇到了一定困难,虽然也会画图,但多是从分数乘法结合图示去分析道理,没有从计数单位平均分的角度分析。对两种类型运算一致性的不确定,导致算法算理的割裂。
●习题三
1.习题内容
(1)算一算

(2)算一算

2.能力指向
主要指向运算能力和推理意识。表现为理解运算对象,探究运算思路,选择运算方法,设计运算程序,求得运算结果。能够借助分子除以整数中的计数单位经验,迁移应用到分数除以分数,将未知转化为已知,培养学生的迁移推理能力。
3.学情分析
二、教学建议
1.激活整数、小数除法“均分计数单位个数”经验,体会除法运算一致性
通过回顾整数、小数除法的算法算理,激活学生“均分计数单位个数”的经验,初步感受运算一致性。例如,可以通过对比整数、小数除法的计算方法和计算道理,总结出都可以通过计数单位来表明算理。从而猜想分数除以整数是不是也有这样的一致性呢?通过对比引发迁移和推理,在猜想中直奔本课主题,初步体会到迁移、类比在数学学习中的重要作用,初步感受运算一致性,体会理法相融,让后续从计数单位角度来探究有“法”可依。
2.沟通“个数均分”和“计数单位均分”的内在联系,经历算法之间一致性过程
分数除以整数主要有两种方法:一种是分子除以整数,一种是乘整数的倒数。由于这两种方法相差较大,学生在理解“一致性”的过程中出现了困难,只有沟通两种方法之间的内在关联,才能更进一步体会分数除以整数的一致性。例如,若用分子4÷2,分母不变得到的算法,它的道理是把4 个计数单位平均分。若用乘整数的倒数的算法,结合图示其实就是把原来的计数单位均分了,得到了新的计数单位最后得到4 个。所以乘整数的倒数的算法若从计数单位的角度,即把计数单位均分。通过“个数均分”和“计数单位均分”的内在关联,经历算法之间的一致性。
3.经历分数除以整数算法迁移,探索同分母分数、异分母分数除法一致性
通过分数除以整数,积累从计数单位探究算理算法的经验,再将该经验迁移运用到分数除以分数中,感悟运算一致性。例如从分子能整除,到分子不能整除,在这个过程中“均分计数单位(个数)”经验的迁移运用。再到同分母分数相除)时,强化学生的推理过程,抓住计数单位说理,迁移运用到异分母分数相除,感悟分数除法的运算一致性。

