一道2021年全国适应性考试题的多角度探究
钟国城
(广东省梅县东山中学,广东 梅州 514017)
题目已知抛物线y2=2px上三点A(2,2),B,C,若直线AB,AC是圆(x-2)2+y2=1的两条切线,则直线BC的方程为( ).
A.x+2y+1=0 B.3x+6y+4=0
C.2x+6y+3=0 D.x+3y+2=0
分析此题以直线与圆、抛物线的位置关系为背景,重点考查处理解析几何问题的思想——“设而不求”,以及学生的计算能力[1].对于此题,可以从三个视角入手求解,一是引入切线方程,利用切线与圆、抛物线的位置关系,求出点B,C的坐标,从而求得直线BC的方程;二是引入点B,C的坐标,寻找坐标之间的关系,最终求出直线BC的方程;三是引入直线BC的方程,根据题设条件求得斜率与截距,故而得到直线BC的方程.本文基于以上三个视角给出七种解法,并得到两个推广,以期对大家有所帮助.
1 解法探究
视角1引入切线AB,AC的方程.
解法1由题可知,抛物线的方程为y2=2x,且过点A的切线斜率存在.
设过点A的切线方程为y-2=k(x-2),
即kx-y+2-2k=0.

所以不妨设切线AB,AC的方程分别为



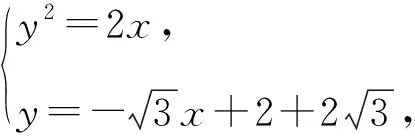


所以直线BC的方程为
即3x+6y+4=0,故选B.
注视角1为解决解析几何问题的常规做法[2],此法运算量较大,尤其考验学生的计算能力.
视角2引入点B,C的坐标.

即2x-(y1+2)+2y1=0.
因为直线AB与圆(x-2)2+y2=1相切,

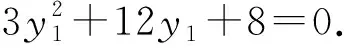

即3x1+6y1+4=0.
同理,3x2+6y2+4=0.
故点B,C在直线3x+6y+4=0上.
所以直线BC的方程为3x+6y+4=0.
故选B.

即2x-(y′+2)+2y′=0.

即3y′2+12y′+8=0.




所以直线BC的方程为
即3x+6y+4=0.
故选B.
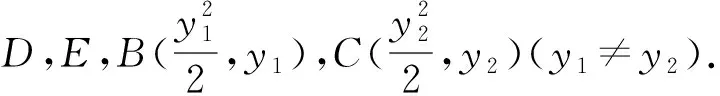

图1 解法4示意图
故∠DAM=∠EAM=30°.
则直线AB,AC的倾斜角为60°,120°.
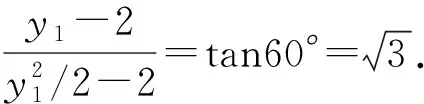


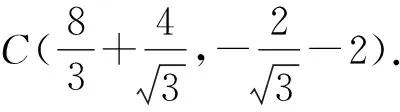
所以直线BC的方程为
3x+6y+4=0.
故选B.
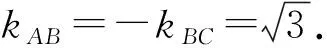
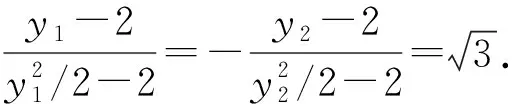



所以直线BC的方程为
即3x+6y+4=0.
故选B.

所以直线BC的方程为


即3x+6y+4=0.
故选B.
注视角2抓住抛物线上的点的坐标,利用坐标和题设条件,转化出坐标之间的等式关系,根据关系最终求得直线BC的方程,此法充分体现了解决解析几何问题的思想——“设而不求”.
视角3 引入直线BC的方程.

设直线BC的方程为x=ty+m,



即3x+6y+4=0.
故选B.
注视角3根据抛物线的特点引入直线BC的方程,结合坐标之间的等式关系,求得直线BC方程中的参数值,从而求得直线BC的方程.
2 解法反思
波利亚说:“掌握数学就意味着善于解题.”在学习数学知识的过程中,不能仅止步于解决问题,应该学会从不同的角度去分析问题,寻找解决问题的不同方法,通过一题多解体会不同知识之间的联系与转化,提高解题能力.通过以上7种解法的探析,不仅可以巩固学生所学知识, 又有效锻炼了学生思维的深刻性、广阔性、灵活性和创新性,提升思维能力,最终达到提升学生数学核心素养的目的.

