“直观想象”素养下的立体几何最值问题求解策略

王芬芬

(江苏省溧水高级中学,江苏 南京 211200)

立体几何,其核心是“立体”问题与“几何”问题,其本质是平面几何的三维化,是代数问题的几何化.立体几何的考查中常常涉及距离、角度、面积和体积等最值问题,此类最值问题的考查,往往与其他多个模块的知识融合交汇,如平面几何、函数、向量等,因此备受命题者青睐.此类问题的求解,不仅需要丰富的空间想象能力、扎实稳定的运算能力,还需灵活运用转化与化归、数形结合等方法将动态问题静态化、空间问题平面化、几何问题代数化.这些等价转化都是建立在学生对空间几何体的精准认识、熟练认知的基础上,同时要求学生必须具备“直观想象”素养.

1 借助直观想象,动态问题静态化

《普通高中数学课程标准(2017年版)》指出,直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养[1].数学教学要注重培养学生的直观想象素养.正如史宁中教授所说:“数学的结论常常是‘看’出来的,不是‘证’出来的.这种‘看’依赖的就是数学直观.直观不是‘教’出来的,而是学生自己‘悟’出来的,这就需要经验积累.”教材,便是学生经验萌生的摇篮.新课标新要求下的新高考,对立体几何问题的命制充分体现了以各版本教材为基础,将核心素养融入试题.因此,教学时教师应充分利用好教材中的例题和习题,深度挖掘教材中隐含的数学思想和数学方法,帮助学生积累解决问题的经验,切实提升学生的数学核心素养[2].

链接教材(人教A版必修二119页练习第3题)将一个棱长为6 cm的正方体铁块磨制成一个球体零件,则可能制作的最大零件的体积为____.

解析当球与正方体内切时体积最大,为36πcm3.

评析从问题表象看是一个将正方体磨制成球体、从外向内、削棱去角的过程,问题的实质可以看成正方体内部有一个球,不断膨胀后达到极限状态——与正方体的六个面均相切,即为正方体的内切球时不能再膨胀.这是一个借助几何直观,通过寻找临界状态,将动态问题转化为静态问题,即“化动为静”的过程.

案例1已知四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,现将四面体ABCD放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,则圆锥侧面积的最小值为____.

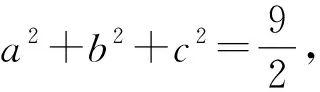
2 借助直观想象,空间图形平面化

空间问题平面化即降维是处理立体几何问题的一种重要的思想方法．空间问题平面化,就是将空间的点、线、面的关系平铺到同一平面上进行研究,在这个平面中将已知和目标的各个元素串联在一起,通过研究各元素间的关系,使得空间问题转化为平面问题.

案例2已知某圆锥的母线长为3,底面半径为1,则该圆锥的体积为____.设线段AB为该圆锥底面圆的一条直径,一质点从A出发,沿着该圆锥的侧面运动,到达点B后再沿侧面回到点A,则该质点运动路径的最短长度为____.

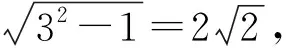
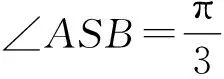
评析曲面上路径最短问题,可以借助平面上的常用结论——两点间距离线段最短,借助几何转化,将曲面问题化为平面问题——化曲为平.既然有化曲为平,那折线段最短问题又怎么解决?

案例3(多选)如图1所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,P是A1B上的一动点,则( ).

图1 案例3图 图2 案例3解析图

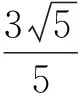
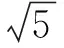
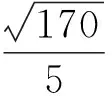
解析(1)求DP的最小值即求点D到线段A1B的距离,在等腰△A1BD中利用等面积即可求,选A.

(2)解决折线段和最小问题,教师可先给出如下引导问题:

一个质点在长方体表面从点A出发运动到点C1的过程中,运动的最短路径长度为____.

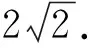
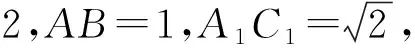
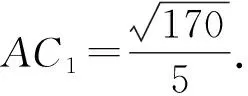
评析折面上路径和最短问题,依然可以类比前面已经解决了的曲面上线段最短问题的解决策略——化折为直.将折面沿交线展开平铺,这样折线段最短就可以转化为直线段长度和的问题,此转化可以将立体几何问题化归为平面几何问题.

3 借助直观想象,几何问题代数化

代数重点研究数字和文字的代数运算理论和方法;几何主要研究空间结构及性质.代数与几何相辅相成,融为一体.通过转化与化归,我们可将立体几何的最值问题转化为函数最值,借助函数求出最值.

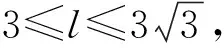
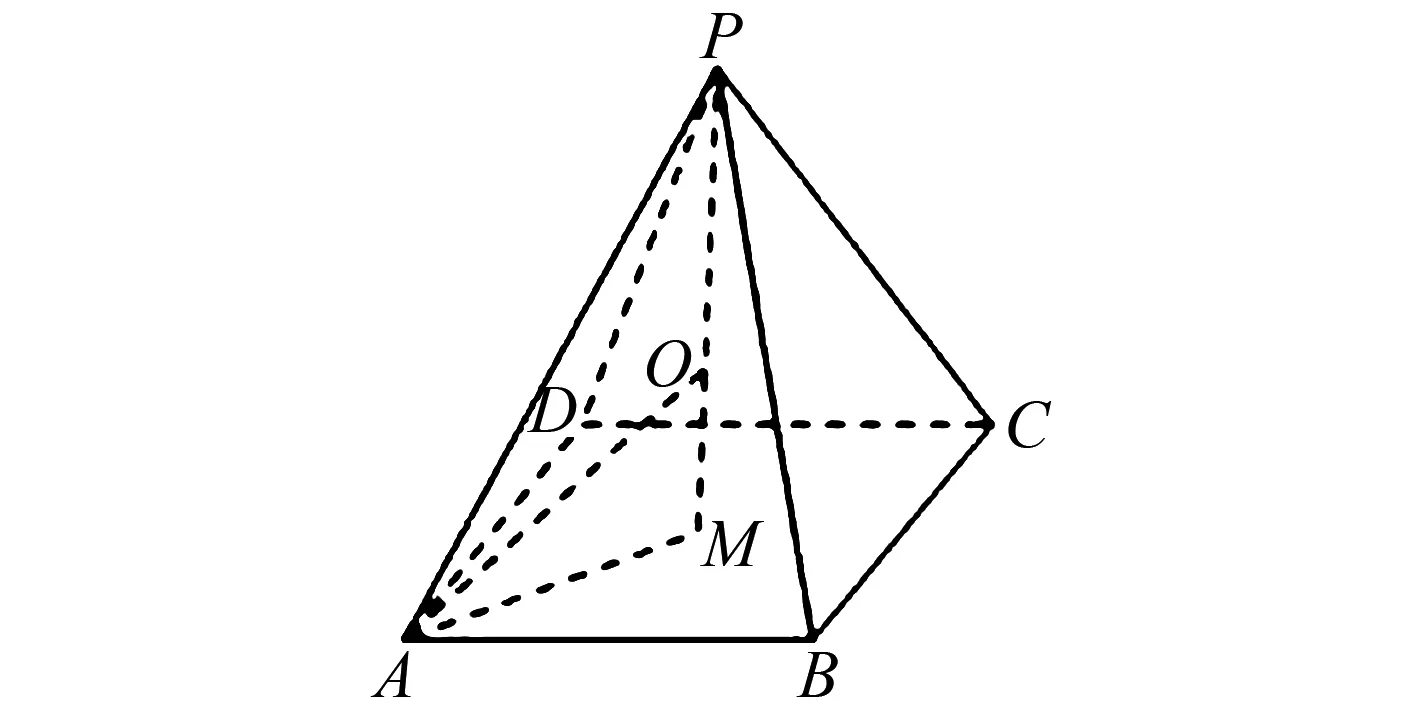
图3 正四棱锥高为变量

评析该题考查的是锥体体积的取值范围的求解问题,可以引入两个变量,借助两个变量之间的等量关系先消元,再通过求导判断出目标函数的单调性,从而求出目标函数的值域,即将几何问题代数化来解决立体几何中的最值问题.

基于直观想象的立体几何最值问题的解决,改变了原有问题的抽象状态,将问题具体化、形象化,使学生在解决问题的过程中不再是面临冰冷的数学符号和图形,而是通过直观想象加强了问题的可视化、可解化,使学生在问题的解决过程中推动了数学抽象、逻辑推理、数学运算、数学建模、数据分析等素养的培养.因此,立体几何教学中,我们应该继续专研教材教法,重视知识的交汇,将直观想象落到实处,促进学生核心素养的提升,让想象与推理并重,几何与代数齐飞.