块对角引导的多视角统一图聚类
梁毅聪,张 巍,滕少华
(广东工业大学 计算机学院,广州 510006)
1 引 言
多视角数据广泛应用在很多实际的场景中[1-3],例如一个多媒体片段可以使用视频和音频来表示;对于同一篇报道可以有多种评论描述.一般来说,多视角数据可以比单视角数据提供更加完整的信息,所以,充分挖掘多个视角数据的信息可以提升聚类的效果.但是,传统的聚类算法,例如kmeans[4],DBSCAN[5],谱聚类[6]等,大多仅仅针对的是单视角数据.因此,多视角聚类算法吸引了越来越多学者的关注.总的来说,现有的多视角聚类方法大致可以分成5种类别[7]:多视角基于图的聚类[8,9],多视角谱聚类[10],协同训练式聚类[11],多核聚类[12],多视角子空间聚类[13].在这些方法中,多视角基于图的聚类方法会利用图结构可以方便有效地表示对象关系的特点,通过多个视角数据样本信息学习到一个统一相似图,然后再使用该图去进行聚类.Nie等[14]对每一个视角的相似度图引入自适应权重来构造统一相似度图.Wang等[15]先通过数据样本之间的距离构建每一个视角的相似度图,然后融合所有视角的相似度图得到统一相似度图.最近,为了挖掘出多视角之间更多的关系,多视角一致性与不一致性也逐渐成为热点话题,同时其也被引入到了多视角聚类当中[16,17].
虽然多视角聚类上有了很大程度的进展,但是还存在一些问题需要探讨:1)多视角不一致性临界值难以确定.在多视角一致性与不一致性探索上,一些方法仅仅寻求多个视角的一致性,此时,多视角的不一致性的临界值往往定义得不够准确(部分不一致性部分混入一致性部分当中);2)非同族关系负面影响.构建出来的相似度图还是会受到很多零散的非同簇关系的影响,从而导致不理想的聚类效果;3)簇块结构丢失.由于各个视角相似度图的质量无法完全保证可靠,此时,可能会使最终的相似度图丢失某些簇块结构,严重影响最终的聚类效果.针对这些问题,本文提出块对角引导的多视角统一图聚类MUGC-BD(Multi-view unified graph clustering guided by block diagonal).该方法首先在各个视角相似度图之间引入不一致性关系来构造出多视角一致性部分,再而融合学习一个相似度图;最后在该相似度图中加入块对角引导与图的连通分量约束,这使得在减少非同簇关系影响的同时以及在单个视角相似度图出现较大偏差时,还能保证一定的有效性.设计了对应的交替优化算法对MUGC-BD进行求解,在6个数据集上进行对比实验验证了本文方法的有效性.
2 相关工作
为了叙述方便,在此先给出相关符号的定义.假定含有v个视角的多视角数据={X1,…,Xv},每个视角对应的相似度图为={Z1,…,Zv},αi代表第i个视角的权重,.代表Frobenius 范数的平方,Tr(·)代表迹函数,A≥0表明矩阵A的所有元素都大于等于0,c代表聚类类别簇的个数,θn×n代表一个维度为n×n元素全为1的矩阵.
2.1 多视角一致性与不一致性
最近,多视角一致性与不一致性也吸引了越来越多的关注[13,18-21].因为其可以更加完整地描述多视角数据中的对象.一般而言,针对某一个对象,不同的视角之间必存在着一致与不一致的部分,而利用这些信息可以更好地准确地把握对象与对象之间的关系,从而得到更好的聚类效果.在建模形式上,多视角的一致性与不一致性可以简单分为数据样本特征的一致性与不一致性;数据关系的一致性与不一致性.Luo等[13]先利用多视角数据求解出子空间表示,然后将该表示分解成一致性图与视角特有的不一致性图.Liang等[18]分别对多视角相似度图的一致性与不一致性建模,并融合一致性图得到统一相似度图.Liu等[19]引入视角一致谱嵌入和视角特定谱嵌入来探索视角间与视角内的关系.Liang等[20]利用非负矩阵分解来构造一致性潜在空间和视角特定的潜在空间.Li等[21]考虑在数据空间构建一致性和视角特定的不一致性并同时学习聚类标签.在聚类中,一般主要考察的是样本之间的关系,同时常常会使用图结构来表达.由此,本文可转为探讨相似度图中一致性与不一致性部分.
2.2 统一相似度图的构建及其优化
多视角基于图的聚类方法一般会构造一个统一相似度图来进行聚类,所以,不少学者对于如何融合各个视角的信息也作了一些研究[14](本文主要针对如何融合多个视角的相似度图).基于直观的经验,可以想到的是统一相似度图应该为所有视角相似度图的平均(例如ILRSOMMSC[22],LRRGL[23]),即为:
(1)
显然,这样构建统一图健壮性不高,因为它没有考虑到某些视角的相似度图可能存在极大的偏差,由此便出现了进一步的优化[18].
(2)
可以看出,这种图融合的方法,考虑到了每一个视角对于统一图的贡献,相对于式(1)更为合理.本文也将采用此方法来融合所有视角的一致性部分.Liu等[24]对得出统一相似度图进一步作了稀疏约束,降低了噪声,但是通过这种做法,很可能会破坏原有比较弱的一些簇关系结构,在本文中,将使用块对角引导与连通分量约束减少这种情况的出现.
3 块对角引导的多视角统一图构造
3.1 体系架构图
MUGC-BD整体架构见图1.其大致思路为首先将每一个视角的相似度图分解成一致性部分与不一致性部分;其次令每一个视角的不一致性部分哈达马积的和尽可能小来构造不一致性关系;然后融合所有视角的一致性部分;并加入块对角引导与连通分量约束,最终得到统一相似度图.
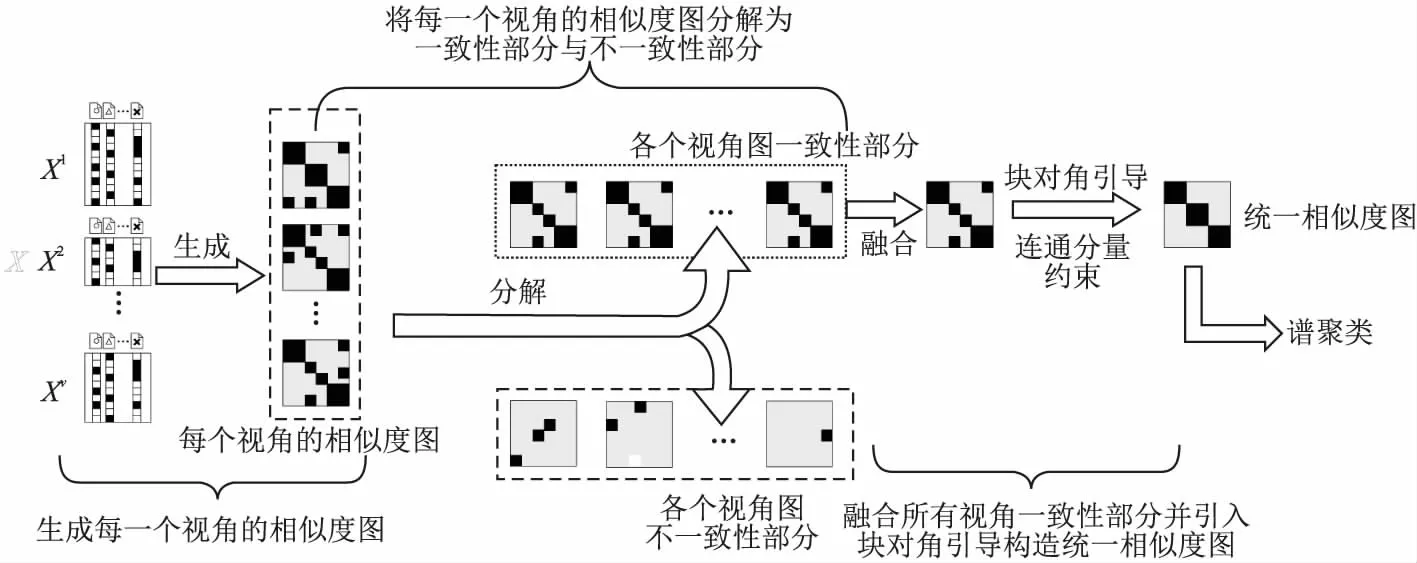
图1 MUGC-BD架构图
3.2 多视角图的一致性与不一致性
多视角图的一致性与不一致性实质上就是利用相似度图作为介质来构建多视角的一致性与不一致性,由于每一个视角的相似度图中必定存在一致性和不一致性部分.因而本文不妨假定相似度图为一致性与不一致性部分的和,公式表示为:
Zi=Ai+Dii=1,…,v
(3)
其中,Zi代表第i个视角的相似度图,Di代表第i个视角相似度图的不一致性部分,Ai代表第i个视角相似度图的一致性部分.
Zhao等[25]分别利用子空间构造出每一个视角的相似度图,然后作带权图融合得到一致性公共图.Meng等[26]使用潜在子空间构造出一致性结构,并在该一致性结构中加入稀疏低秩约束.Tang等[27]直接先构造出每一个视角的相似度图,然后使用哈达马积来寻求一致性,最终合成统一相似度图.上述的大多方法,都是直接对多视角关系作一致性而很少明确探求不一致性,即仅仅探索一致性关系.此时,不一致部分的临界值往往定义得不够准确,所以应该考虑对不一致性关系建模.参考SGF[18],CSMVC[24],同时结合式(3),视角间的不一致性关系可以建模为:
(4)
αi代表第i个视角的权重,°代表哈达马积,sum(·)表示矩阵中所有元素的和.显然,通过对不一致性关系的构建能更加准确得到各个视角对应的不一致性部分,再结合式(4)中一致性部分与不一致性部分的关系,明显可以进一步得到更加纯净的一致性数据部分.同样地,本文也依此构建不一致性关系.
3.3 块对角引导
如果一个相似度图中嵌有簇结构的话,那么图上可以表现出有一些对角块[28].也就是一个相似度图可以表达为:
S=FFT+Es.t.FTF=I
(5)
其中,E可以代表相似图中的噪声等所造成的偏差.由式(5)式可知,当E→0时,S拥有一个更好的簇结构.式(5)等价于:

(6)
文献[28]中表明了式(6)中FFT的是相似度图的低秩近似,它可以对大的对角块和小的非对角块很好地近似化.在理想情况下,FFT是一个严格的块对角矩阵.而相应的,每一个对角块实质上又是对应一个簇,这就表明了,对相似度图加入块对角引导可以减少非同簇关系的干扰,从而进一步提升聚类的效果.基于此,本文在统一相似度图中引入:
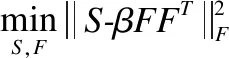
(7)
其中β是一个参数.式(7)主要目的是能引导统一相似度图S拥有较好的簇信息.
3.4 连通分量约束(拉普拉斯矩阵秩约束)
图的连通分量约束主要是为了将类别个数的信息整合入相似度图中,从而能在图上形成与类别个数相同的连通分量,进而提升聚类的效果.Zhan 等[29-31]提出了几个方法整合各个视角的相似度图到一个全局图,并对该全局图使用连通分量约束,使其含有特定数量的连通分量.Zheng等[32]基于Smooth Clustering(SMC)作改进,并引入图的连通分量约束来优化系数矩阵.具体来说,图的连通分量约束主要使用定理1,定理2进行优化求解
定理1.[30]图G的连通分量为k当且仅当其拉普拉斯矩阵L的零特征值的重数为k.
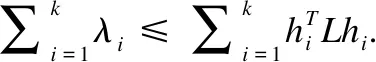
根据定理1,定理2,对于求解图S的连通分量约束可以表示为[14]:
(8)
其中γ是一个参数,当γ足够大时,可以使得约束rank(LS)=n-c满足,与文献[30]类似,本文设定γ=1.迭代求解式(8)使满足连通分量为c.本文主要是在统一相似度图中加入了连通分量约束.
3.5 块对角引导优化
从图1中可以看到,MUGC-BD步骤大致可以分成阶段1:生成每一个视角的相似度图;阶段2:将每一个视角的相似度图分解成一致性与不一致性部分;阶段3:融合所有视角的一致性部分,并引入块对角引导构造统一相似度图.在阶段1中本文使用高斯核与KNN来构造相似度图,此时由于无法获知簇的个数,每一个视角构造的相似度图中都可能存在不正确簇的块对角结构;此时假设一些视角有不正确的结构,那么阶段2这些视角的一致性部分将保留不正确的结构;再到阶段3对一致性部分进行融合时,虽然做带权融合,但是因为融合权重主要取决于视角的一致性部分与统一相似度图之间的差距,也就是说当大部分视角一致性部分结构存在问题时,这些错误将带入到统一相似度图中,从而导致不理想的聚类效果.如图2所示,在Washington数据集下,每一个视角的相似度图并没有很好的表达出簇的关系(见图2(a)、(b)),显然,如果直接融合全部视角的相似度图也不能得到好的效果,而如果增加块对角引导与连通分量约束后,在减少非同簇关系干扰的同时,能形成符合簇个数的连通分量(见图2(c)).

图2 Washington数据集上不同相似度图对比
由此,本文在块对角引导上加入图的连通分量约束,利用簇个数的信息进一步提高统一相似度图的质量.
3.6 目标函数
结合式(2)、式(4)、式(7)、式(8),得到总的目标函数如下:
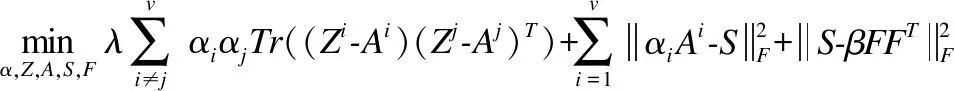
(9)
其中,λ,β为可调参数.通过求解该目标函数得到统一相似度图,然后进行谱聚类得到最终的聚类结果.
4 目标函数优化
4.1 优化算法
参考文献[18],本文也采用一种交替迭代最小化的策略来进行求解.由此,式(9)可以切分成多个子问题:
1)固定A1…Av,F和S, 更新α
当固定A1…Av,F和S时,式(9)可以转换为:
(10)
先去除αi≥0的约束,可以转其为拉格朗日函数:
(11)
其中,α为一个v×1向量,θv×1为一个元素全为1的v×1向量,对其偏导为0可得:
2(λ(θv×v-I)∘G+P∘I)α+μθv×1=u
Gij=Tr((Zi-Ai)(Zj-Aj)T),Pii=Tr(Ai(Ai)T)
(12)
其中,θv×v为一个所有元素都是1的v×v矩阵,I为v×v单位矩阵.令K=2(λ(θv×v-I)∘G+P∘I),可得:
(13)
式(13)可以使用简单的线性代数求解,再而引入约束作投影:
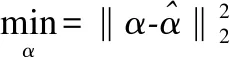
(14)
根据文献[18]可以得到α.
2)固定A1…Av,α和S, 更新F
当固定A1…Av,α和S,式(9)可以转变为:
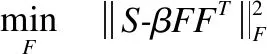
(15)
利用范数的迹转换运算,式(15)等价于:
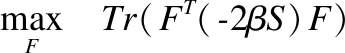
(16)
根据文献[30],可求解得到F.
3)固定A1…Av,α和F, 更新S
当固定A1…Av,α和F,式(8)可以转换为:
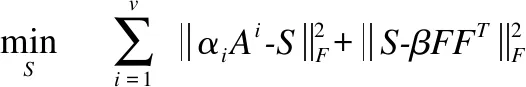
(17)
可以将式(17)转为:

(18)
针对S,求式(18)偏导为0,可得:
(19)
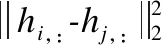
4)固定S,α和F, 更新A1,…,Av
当固定S,α和F,式(9)可以转换为:
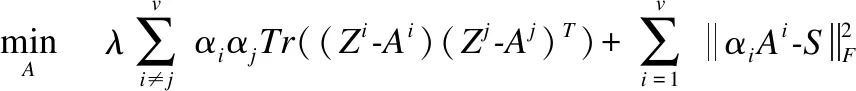
(20)
式(20)求其关于A偏导为0可得:
(21)
类似于求解α,式(21)也转变为简单线性代数形式.
算法1.MUGC-BD
输入:输入多视角数据,簇的个数c,参数λ,β,γ=1
输出:统一相似度图S,最终以S作为输入使用谱聚类得到最后的簇切分
1.构造每一个视角的相似度图(利用高斯核与KNN)
2.初始化Ai=Zi,S=Z1,初始化H通过求解问题(18),初始化F通过求解式(16),i=1,…,v
3.while 没有收敛
4. fori=1,…,v.(F∈Rn×c)
5.求解式(9)更新α,求解式(16)更新F
6.end for
7. do
9.untilS含有c个连通分量
10.fori=1,…,v
11.求解式(20)更新Ai
12.end for
13. end
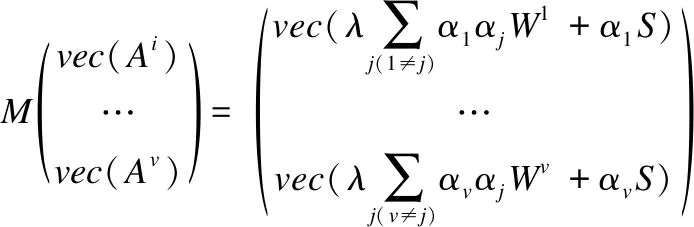
(22)
其中vec(·)代表矩阵向量化操作.最终将Ai作投影,即Ai=max(0,Ai),Ai=min(Ai,Zi).由此,算法1中总结优化目标函数整个过程.
4.2 复杂度分析
此处的复杂度分析,不考虑矩阵加法和直接的矩阵元素的运算操作.那么,在MUGC-BD中时间花费主要来自于矩阵求逆,矩阵乘法,特征值分解.对于更新α时间复杂度大致为O(n3+(v+1)3+(v+1)2).对于更新F时间复杂度大致为O(n3).对于更新S时间复杂度大致为O(t1n3),t1为内层循环更新S时的迭代次数.对于更新A时间复杂度大致为O(v3+v2n2).所以,算法1总的时间复杂度为O(t(t1n3+v3+v2+v2n2)),其中t为迭代次数.
5 实 验
5.1 数据集
本文在6个多视角数据集进行实验验证MUGC-BD的有效性.其中,数据集包括3sources[33],BBCSport4v[33],MSRCv1[18],100leaves[15],Washington[33],CalTech7[24],如表1所示.

表1 数据集描述
5.2 实验设定
为了证实本文方法的有效性,本文在多个数据集中,对比了MUGC-BD与6种方法的效果.Multiview Consensus Graph Clustering[30](MCGC)先构造每一个视角的嵌入矩阵,再而最小化全局图与嵌入矩阵的不一致性并结合图的连通量约束的策略生成全局图.Multiview clustering with graph learning[29](MVGL)利用图的连通量约束先构造出每一个视角的相似度图,然后再将它们融合成一个全局图.Adaptively Weighted Procrustes[34](AWP)在Procrustes Average[35](PA)中引入自适应权重.Weighted Multi-view Spectral Clustering[36](WMSC)利用子空间的最大的标准角作为基准来寻求各个视角的权重并得到指示矩阵.Similarity graph fusion[18](SGF)通过建模一致性与不一致性来学习一个统一相似度图.Consistency sparse multi-view clustering for graph[24](CSMVC)在统一图中引入稀疏以寻求更加纯净统一相似度图.
聚类效果使用常用的5种评价指标:归一化互信息(NMI),准确度(ACC),纯度(PUR),调整兰德系数(ARI),F分数(F-Score).这些指标都是取值越高,代表聚类效果调节参数λ的取值范围[10-6,106],参数β的取值范围[10-6,106].参考文献[18],本文构造每一个视角相似度图时KNN中设定K=15.每个算法运行20次,最终得到均值和标准差.
5.3 实验结果分析
表2展示对比实验的结果,从表中可以得到这些结论:
1)MUGC-BD可以在大多的数据集上聚类效果优于所有的对比方法,特别地,在3sources数据集的各项指标上超第2优的性能7%,15%,4%,26%,18%,这表明了本文方法的有效性.
2)与文献[18]相同,跟没有明确构建多视角不一致性的方法(例如,MCGC,MVGL)相比,有明确构建多视角不一致性的方法聚类效果更好(例如,SGF,CSMVC,MUGC-BD).
3)与SGF相比,CSMVC,MUGC-BD有更好的效果,因为两者都针对统一相似度图作了进一步的优化,减少了统一相似度图所含有的噪声.
4)与CSMVC相比,本文方法在大多数据集获得更好的聚类效果,主要因为MUGC-BD对于噪声的排除更有效,其主要针对的是非同簇关系.另外,CSMVC直接对统一相似度图作稀疏降噪,这表明有可能会破坏原来比较弱的一些簇结构,而通过引入连通分量约束,能够在一定程度上保持正确的簇的块对角结构.
5.4 参数敏感性与收敛性分析
本文模型有参数β,λ,利用实验探究不同的参数取值对聚类效果的影响.如图3反映的是MUGC-BD不同的参数取值在各个数据集上的ACC.显然,在合适的参数组合区间中,MUGC-BD能获得较好的ACC,表明了MUGC-BD对β,λ是相对不敏感的.
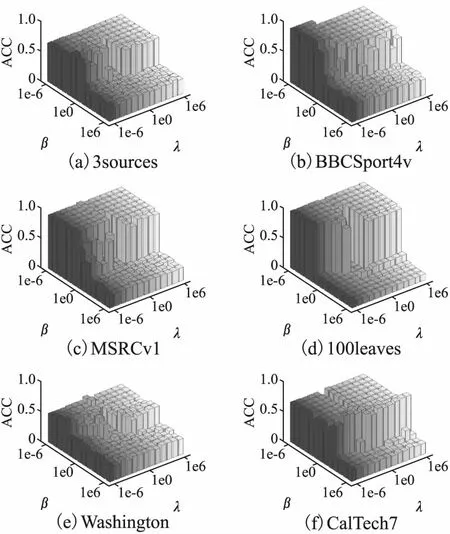
图3 ACC在各个数据集上随λ,β的变化趋势
为了证明MUGC-BD的收敛性,本文展示了目标函数值在多个数据集上随迭代次数的变化曲线,见图4.如图4所示,目标函数值曲线在各个数据集上都能够到达稳定的状态.特别地,MUGC-BD能够在较少的迭代次数就能达到收敛.
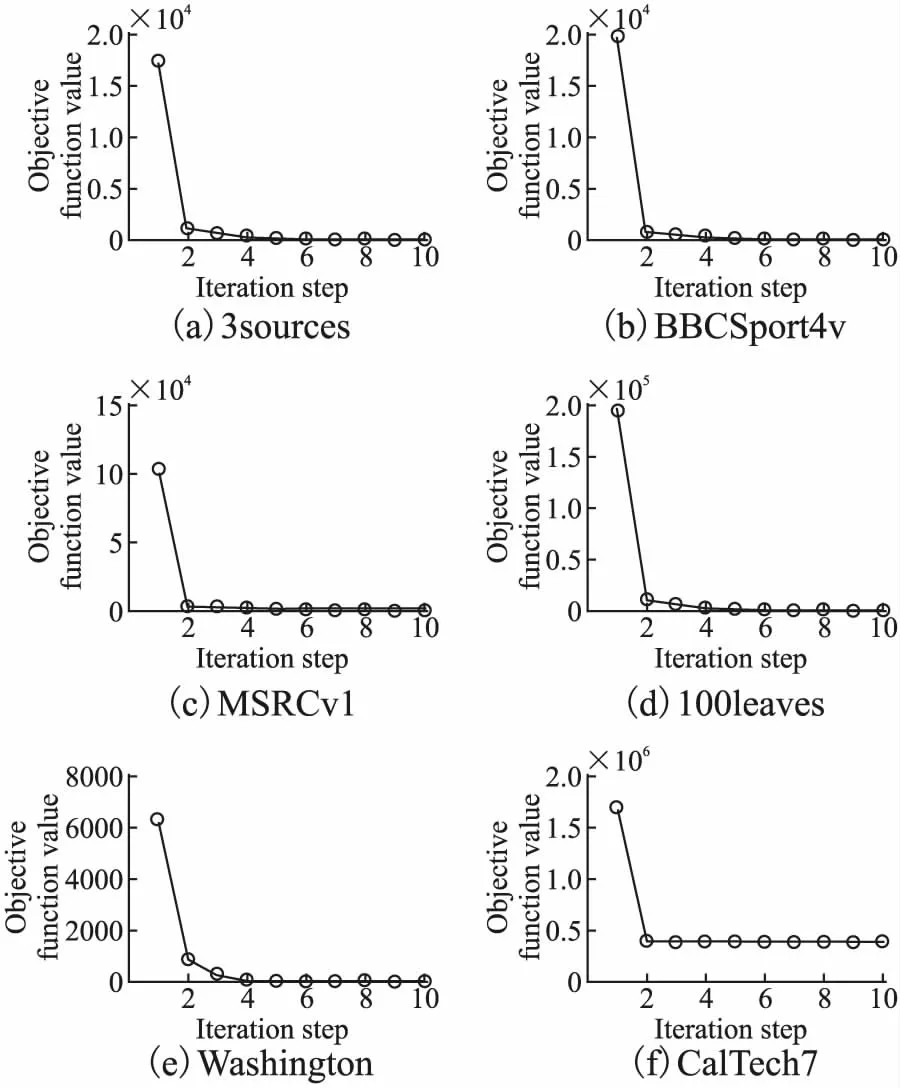
图4 MUGC-BD在各个数据集上收敛曲线
6 结束语
本文表明了相似图中含有良好的块对角结构能够提升聚类的性能,基于此,提出了MUGC-BD.该方法关键是在每个视角中探索多视角不一致性关系,并在构造统一相似度图时引入块对角引导和连通分量约束.通过实验结果可以看出,在多个数据集上,MUGC-BD可以达到较好的聚类效果,验证了本文方法的有效性.但是,本文方法具有较高的时间复杂度,这也是作者未来研究的重点.

