参数自适应的精英变异差分进化算法
林秀丽,李均利,聂君凤
(四川师范大学 计算机科学学院,成都 610101)
1 引 言
差分进化算法(Differential Evolution,DE)是由Storn和Price[1]所提出的一种求解优化问题的全局优化算法.差分进化算法原理简单易于实现,具有鲁棒性强、控制参数少、搜索能力强[2]等优点.它不仅能够解决多模态和非线性函数,还能并行处理大规模问题.因此,该算法广泛应用于机械工程、信号处理、人工智能、数据挖掘和模式识别等多个领域.但在求解复杂优化问题时,随着种群多样性的降低,差分进化算法容易早熟,并且在搜索后期易陷入局部最优值,收敛的精度也会降低.另外,差分进化算法的优化性能[3]对控制参数(如种群大小NP、放缩率因子F和交叉概率因子CR)和变异策略非常敏感.为了解决这些问题,差分进化算法的改进方案主要包括对控制参数的设置、变异策略的选择、结合其他优化算法和实现多种群并行搜索等.
研究者通过参数调整来提高DE的性能,如Draa A等[4]引入了正弦微分进化(SinDE),SinDE采用了两个正弦公式来调整缩放因子和交叉率的值.Deng等[5]试图使用小波基函数来选择参数,仅在部分问题上提高了DE的性能.Cui等人[6]提出了一种参数自适应方案(chDE),其中通过二分法来压缩控制参数空间.另外,Fan and Yan[7]提出一种具有控制参数分区进化和自适应变异策略的自适应DE算法,其中变异策略随着种群进化而自动调整,控制参数在各自的区域内进化,以自适应地发现近似最优值.自适应控制参数是指在迭代过程中的每个阶段应选择合适的控制参数进行迭代,这可以加快收敛速度,减少陷入局部最优值的概率.但是,通常这样的操作会增加算法的时间复杂度;研究者通过变异策略来提高DE的性能,如Wang 等[8]将复合策略应用到DE中,在深入研究现有变异算子和参数的性质后,提出了复合差分进化算法(CoDE).CoDE在3种不同的变异策略中随机选择一种来执行变异操作.Duan等[9]提出了一种具有双重偏好学习变异(DPLDE)的差分进化算法.吴文海等[10]提出了一种基于随机邻域变异策略和广义反向学习的自适应差分进化算法,将邻域的概念引入到差分进化算法中,并将局部邻域变异和全局邻域变异结合为一种新的策略.虽然差分进化算法的各种变异策略可以获得更高的收敛精度和更快的收敛速度,但在求解复杂优化问题时容易陷入局部最优;研究者结合变异策略和参数自适应来提高DE性能,如Yi等[11]人利用混合变异策略操作和自适应控制参数提出了一种新的差分进化算法,该算法将种群分为两部分.Fan等[12]提出了一种具有策略自适应和基于知识的控制参数(SAKPDE).在该算法中,采用了一种学习遗忘机制来实现变异和交叉策略的自适应.Sun等[13]为了提高差分进化算法性能,提出一种新的高斯变异算子和一种改进的突变算子来协同产生新的变异向量,并利用非周期函数和高斯函数分别生成所需的比例因子值和交叉率值,部分工作主要集中在控制参数的自适应策略上.然而,没有免费午餐定理[14]指出,没有一个算法可以解决所有类型的优化问题.如果可以将其他算法的优势融入差分进化算法中,充分利用各自的优势进行协同搜索来提高优化性能.研究者提出结合其他算法来提高DE的性能,如Chen等[15]人将混合粒子群算法和标准差分算法结合提高DE算法的搜索能力.Pan等[16]将蛙跳算法和标准差分进化算法提升算法性能.另外,Jia等[17]提出了一种结合蚂蚱算法(GOA)来提升差分算法(jDE),称为GOA_jDE.
本文通过调整参数和调整变异策略的方法来提升DE的性能,为了进一步加快收敛速度而不增加时间复杂度并且提高差分进化算法的准确性和稳定性,于是本文提出了一种参数自适应的精英变异差分进化算法(A parameter Adaptive Elite Mutation Eifferential Evolution algorithm,AMEDE).AMEDE算法,在基本变异策略(DE/rand-to-best/1)的基础上设计了一种新的精英变异策略(DE/rand-to-elite/1).首先,将精英变异策略与新引入的权重因子控制参数相结合,采用精英变异策略(DE/rand-to-elite/1)进行变异操作,可以有效地避免收敛早熟,有利于搜索较大的空间,从而找到更有前途的区域,其目的是提高算法的搜索效率.最后,利用参数自适应的学习方法对控制参数进行动态调整设置,目的是为不同的优化问题选择不同的参数来求解全局最优值.这有利于加快收敛速度,降低时间复杂度,提高优化性能.
2 标准差分进化算法(DE)
差分进化算法是一种基于群体差异的启发式并行搜索方法,作为一种基于群体导向的随机搜索技术,差分进化算法的执行过程主要包括4个部分:初始化种群、变异操作、交叉操作和选择操作.
2.1 初始化种群
若优化问题的目标函数为min(f(x)),搜索空间为s∈R.DE采用一个D维的向量(M)作为优化问题的初始解.设置种群大小(NP),每个个体都是解空间中的一个候选解,个体可以表示Xi,G={X1,X2,X3,…,Xm},i=1,2,3,…,NP.NP表示种群数量,M是候选解个数.在问题搜索空间范围内[xmax,xmin],采用随机方法生成个体如公式(1)所示:
xi,G=xmin+rand(0,1)*(xmax+xmin)
(1)
公式中,G表示第G次迭代的解,xmax表示问题搜索空间的上限值,xmin表示搜索空间的下限值.rand为[0,1]之间的符合正态分布的随机数.
2.2 变异操作
差分进化算法通过变异操作产生新的变异个体向量vi=[vi,1,vi,2,vi,3,…,vi,G],通常情况下采用以下变异策略进行变异操作:
1)DE/rand/1
vi=xr1+F×(xr2-xr3)
(2)
2)DE/best/1
vi=xbest+F×(xr1-xr2)
(3)
3)DE/current-to-best/1
vi=xi+F×(xbest-xr1)+F×(xr2-xr3)
(4)
4)DE/best/2
vi=xbest+F×(xr1-xr2)+F×(xr3-x4)
(5)
5)DE/rand/2
vi=xr1+F×(xr2-xr3)+F×(xr4-x5)
(6)
其中,r1,r2,r3,r4,r5∈{1,2,3,4,5,…,NP}并且r1≠r2≠r3≠r4≠r5;F是一个重要的控制参数,放缩率因子F∈[0,1]主要是用来控制差分向量的幅度.xbest=[xbest,1,xbest,2,…,xbest,G]表示当前种群中的最佳个体.在变异策略(例如:DE/rand/1)中,向量xr1表示偏差扰动向量,也称为基向量,xr2,xr3是方向向量,xr2-xr3视为差向量.差分进化算法的变异策略是将种群中的两个个体之间的加权差向量加到基向量上所产生的,相当于在基向量上加上了一个随机偏差扰动.实际上,可以将基向量作为搜索区域的中心点,利用差分向量设置搜索方向,利用放缩率因子控制步长.
2.3 交叉操作
交叉操作是采用变异后得到的变异个体vi,G和目标个体xi,G进行交叉后得到目标个体的候选个体ui,G.在差分进化算法中,交叉策略为二次项交叉,如公式(7)所示:
(7)
式中randj∈[0,1]为服从均匀分布的随机数,交叉因子CR∈[0,1]也是进化算法中的一个重要控制参数,根据交叉因子进行交叉操作.
2.4 选择操作
差分进化算法采用贪婪算法更新下一代种群中的个体,更新为公式(8)所示:
(8)
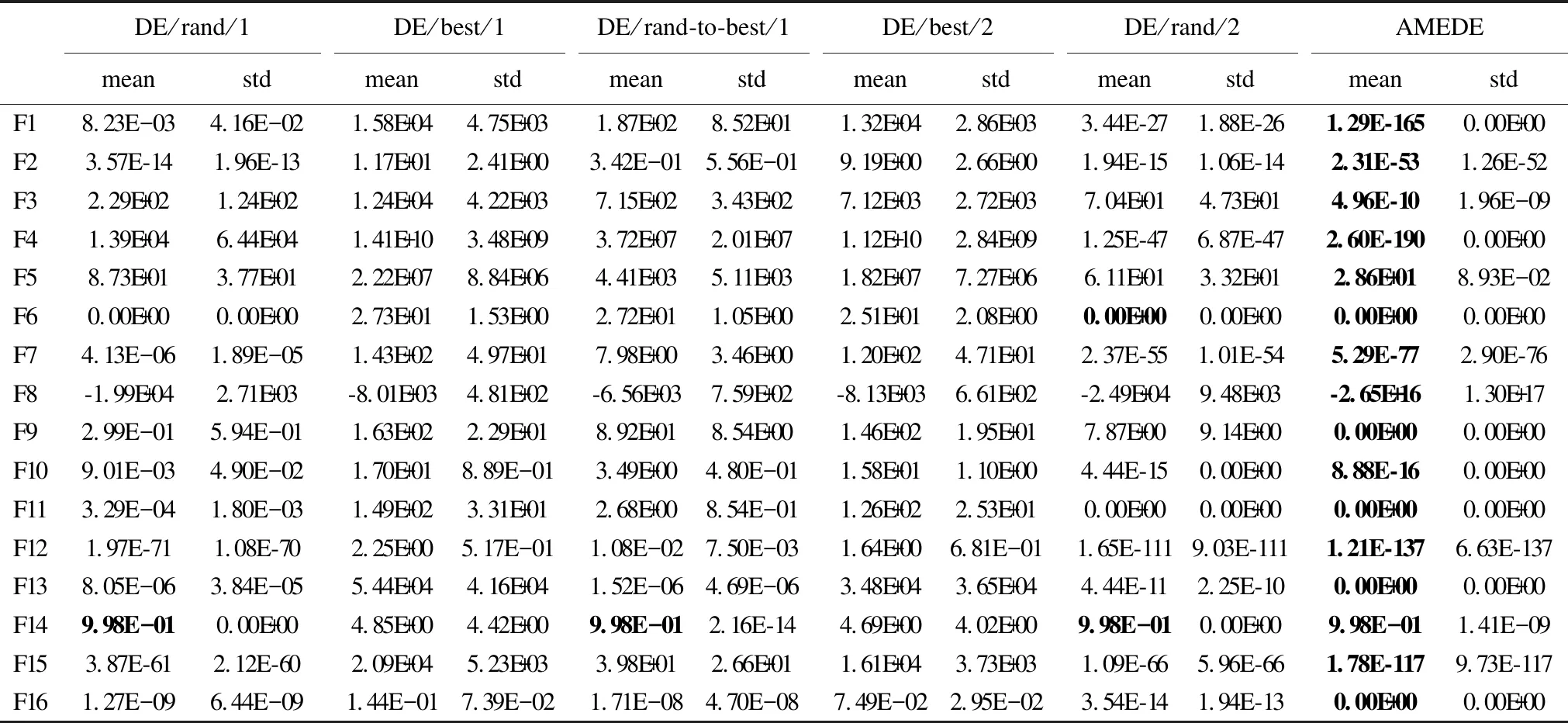
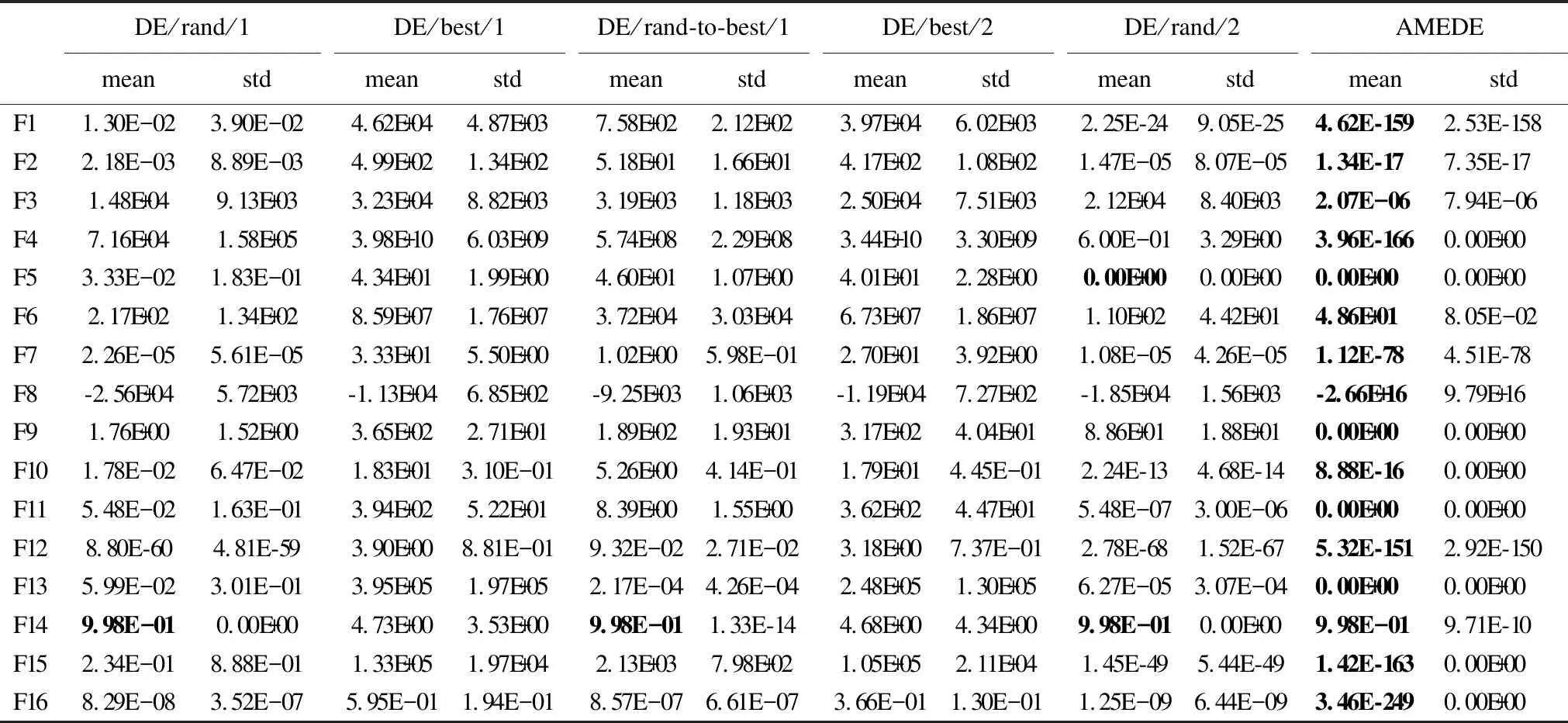
3 参数自适应的精英变异差分进化算法
3.1 精英变异策略
在差分进化算法中,变异策略的选择和控制参数的设置直接影响到算法的探索能力、收敛精度和速度.为了解决这个问题,在精英变异策略中引入新的权重因子ω,以确保个体收敛,并采用精英个体替代最优个体的方法增加种群搜索范围.在每一代进化过程中,算法从当前种群中选择出n个个体组成精英组,并从精英组中随机选择其中一个个体作为精英个体.精英个体指的是种群中优秀的个体,精英个体对种群的进化起着推动性作用.精英变异策略“DE/rand-to-elite/1”,具体可以表示为公式(9):
Vi=ω·Xi+F·(eliteX-Xi)+F·(Xr1-Xr2)
(9)
式中ω为(0,1)范围内的权重因子,由于在DE中较大的Xi值可能导致个体发散,不利于收敛,如图1所示.eliteX为种群中适应度值最小的前百分之十的个体之中的一个随机个体则称为精英个体,计算公如下:
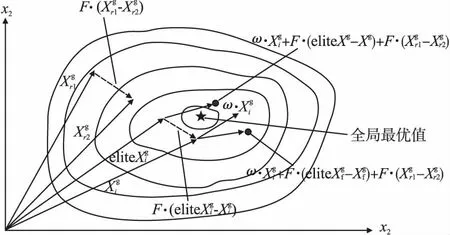
图1 AMEDE算法变异策略
eliteX=rand(sort(Fitness(Xi))*10%)
(10)
3.2 参数自适应策略
为了使控制参数值的选择不受具体优化问题的影响,本文提出了一种改进的控制参数自适应策略,在AMEDE算法中,每个个体都有属于自己的控制参数,其包含权重因子ω,放缩率因子F和交叉率因子CR,并使其在进化过程中进行动态调整,如图2所示.与传统的差分进化算法(DE)中采用固定的控制参数值相比,参数自适应调整策略更有利于种群进化.本文也充分利用了进化过程中精英个体的信息,在参数自适应策略中提出了两种控制参数学习的方法,分别是全体学习法和重置参数法.
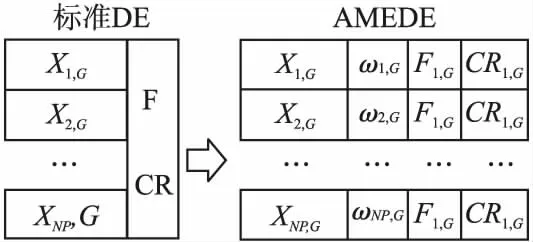
图2 AMEDE算法参数自适应
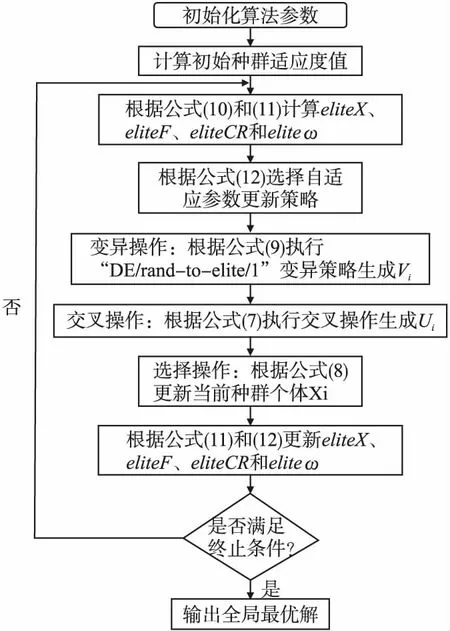
图3 AMEDE算法流程图
3.2.1 控制参数学习方法
“三人行,必有我师焉,择其善者而从之,则其不善而改之”,人和动物都可以模仿、学习优秀的对象来进步.这一现象也可以应用到本文的控制参数学习中,学习种群中表现优异的个体.本文中表现优异的个体称为精英个体,利用精英个体的控制参数信息,更新其他个体的控制参数.
将个体中按照个体适应度进行从小到大的排序,对种群中个体适应度值排名后40%的个体的控制参数按照以下操作进行更新.
操作1.全体学习
充分利用精英个体的信息,在本文中如果精英个体的位置是优秀的,那么精英个体的控制参数也是优秀的.本文利用适应度值排名前五的个体的平均控制参数来更新自身的控制参数,更新如公式(11)和公式(12):
eliteCPG=top5(Fitness(XG))
(11)
CPi,1G+1=CPiG+r·(mean(eliteCPG)-CPiG)
(12)
式中,Fitness(XG)表示当前种群的适应度值,在本文中适应度值越小说明全局最优值越优秀,eliteCPG={eliteFG,eliteCRG,eliteωG},利用适应度值取出排名前5个个体的控制参数值,CPiG表示个体i的控制参数向量[Fi,1G,CRi,2G,ωi,3G],r为(0,1)之间的随机数,mean(eliteCPG)为适应度排名前五的个体的控制参数的均值.
操作2.重置参数
在执行全体学习控制参数时可能陷入局部最优导致过早收敛,从而降低了种群多样性.因此,合理控制种群多样性可以对一部分个体进行重置参数如公式(13):
(13)
式中,R表示一个3维的随机向量,每个维度的取值范围为(0,1).“o”表示将对应元素相乘.CPU为各控制参数的上限值,CPL为各控制参数的下限值,本文中PU=[0.9,0.9,0.9],PL=[0.1,0.1,0.2].
3.2.2 概率阈值自适应策略
在迭代过程中,通过计算种群中个体适应度值的多样性概率阈值公式(14)来选择控制参数学习方法中的操作1或者操作2:
τ=fitness(bestX)-mean(fitness(X))
(14)
式中,fitness(bestX)表示每一代中的最优适应度值,mean(fitness(X)为平均适应度值.τ是0和1之间的实数.如果τ值越大,则个体相似性越低,那么个体差异大,种群多样性越强.反之,如果τ值越小,说明个体相似性越强,那么种群多样性降低.本文中利用概率阈p值判τ的大小,则概率阈值自适应策略可以表示为公式(15):
(15)
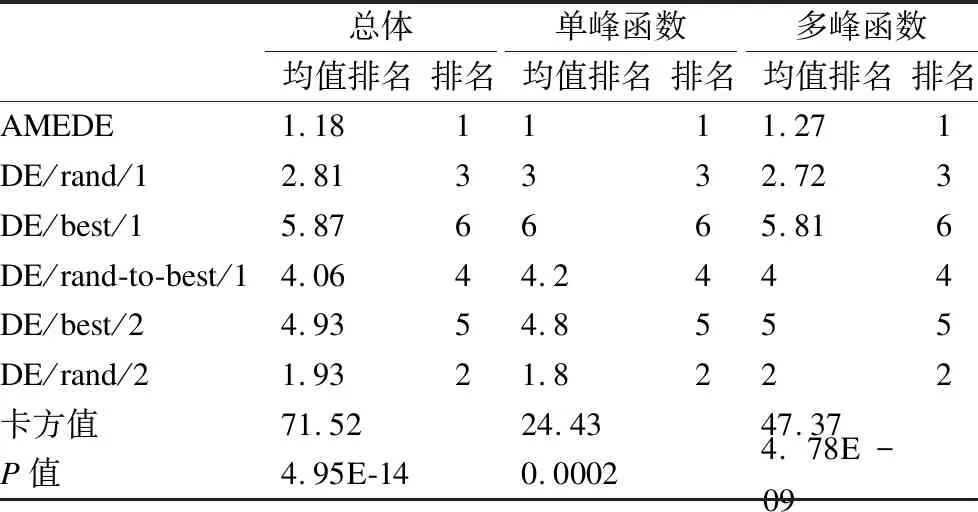
根据以上分析可以得出两种情况:1)当前种群呈现良好的多样性时,保持当前控制参数向精英个体参数学习,这有利于更快收敛到全局最优值;2)当种群多样性下降,应调整和重置一部分控制参数值,以便产生新的后代个体.这些新的后代个体将有利于提高当前种群的多样性,帮助个体摆脱局部最优,从而避免过早收敛.因此,控制参数值的调整规则既保持了种群多样性,又保证了算法的收敛性能.
3.3 AMEDE算法流程
3.3.1 AMEDE算法的伪代码
输入:目标函数f,最大迭代次数M,问题维度D,问题搜索空间(l,u),种群大小NP,控制参数变化范围CPU、CPL,交叉策略CS和变异策略MS
输出:全局最优解
Step 1. 随机初始化种群中个体的位置X、初始化控制参数CP值、初始化精英个体eliteX的位置
Step 2. 将迭代器i=0,M=1000
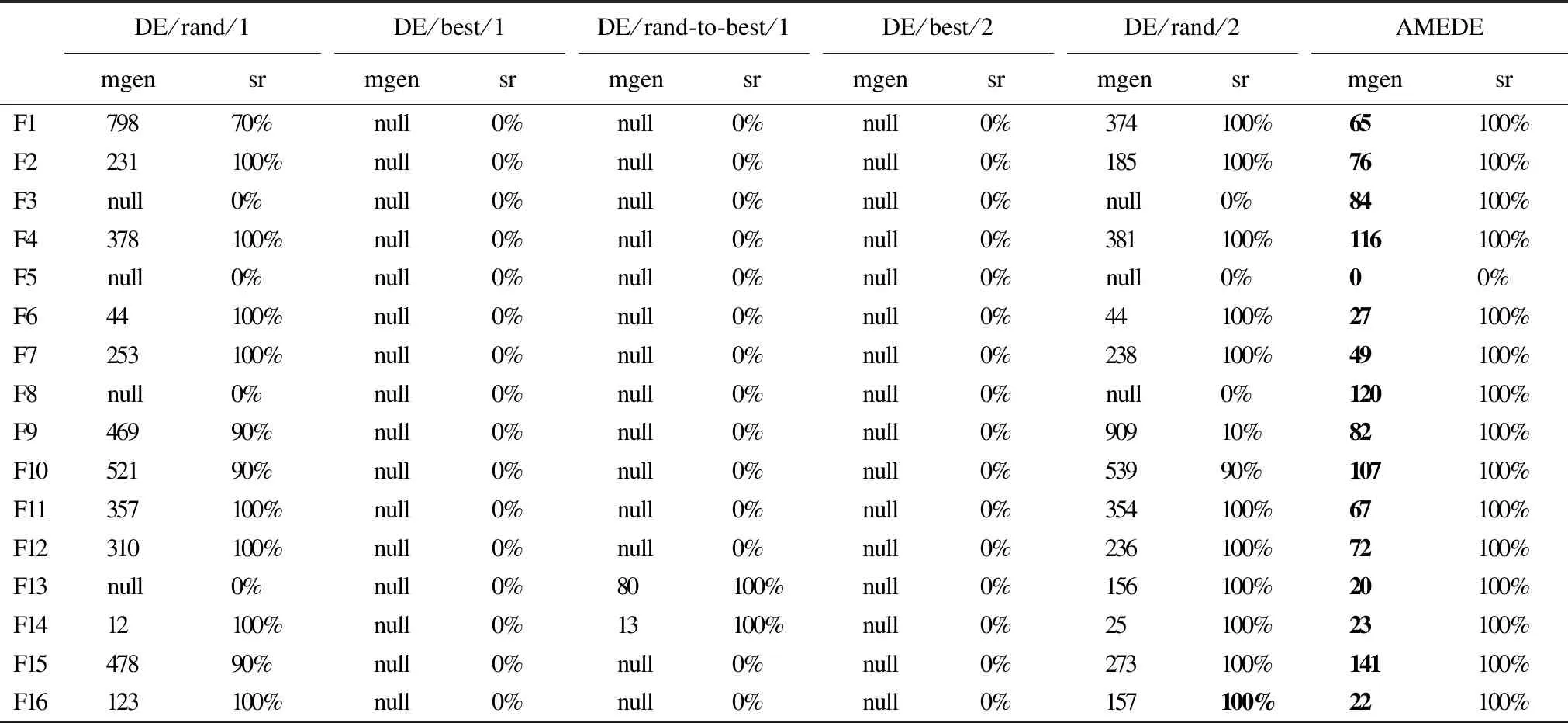
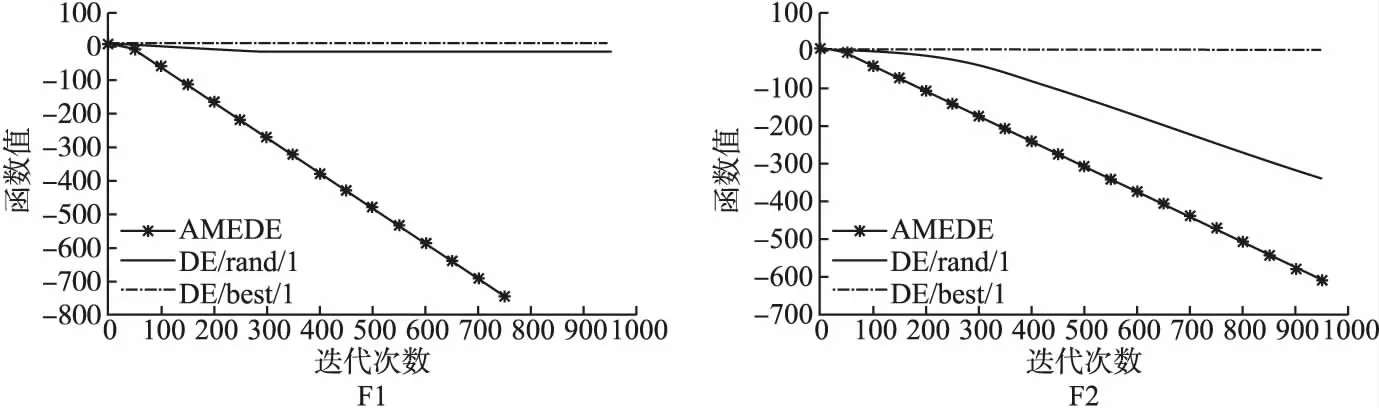
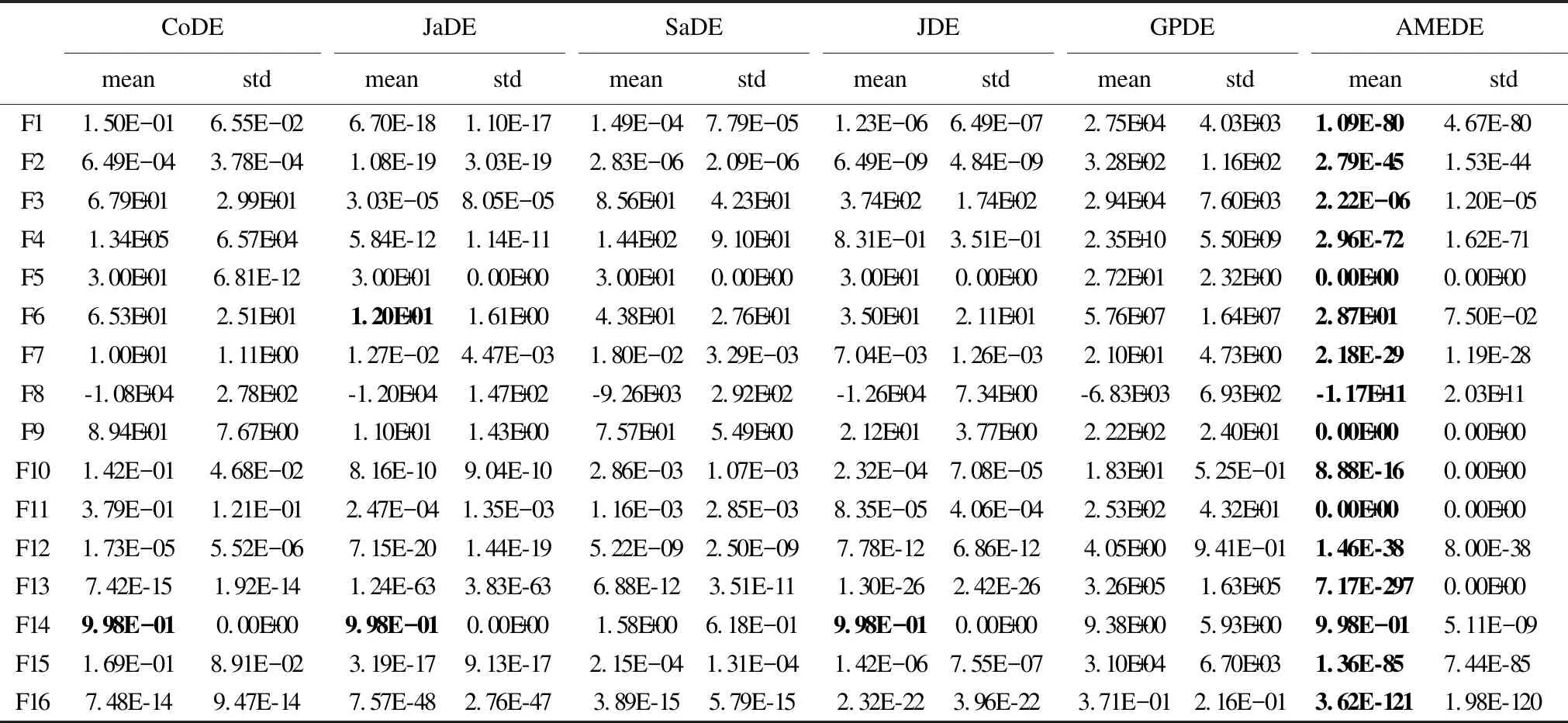
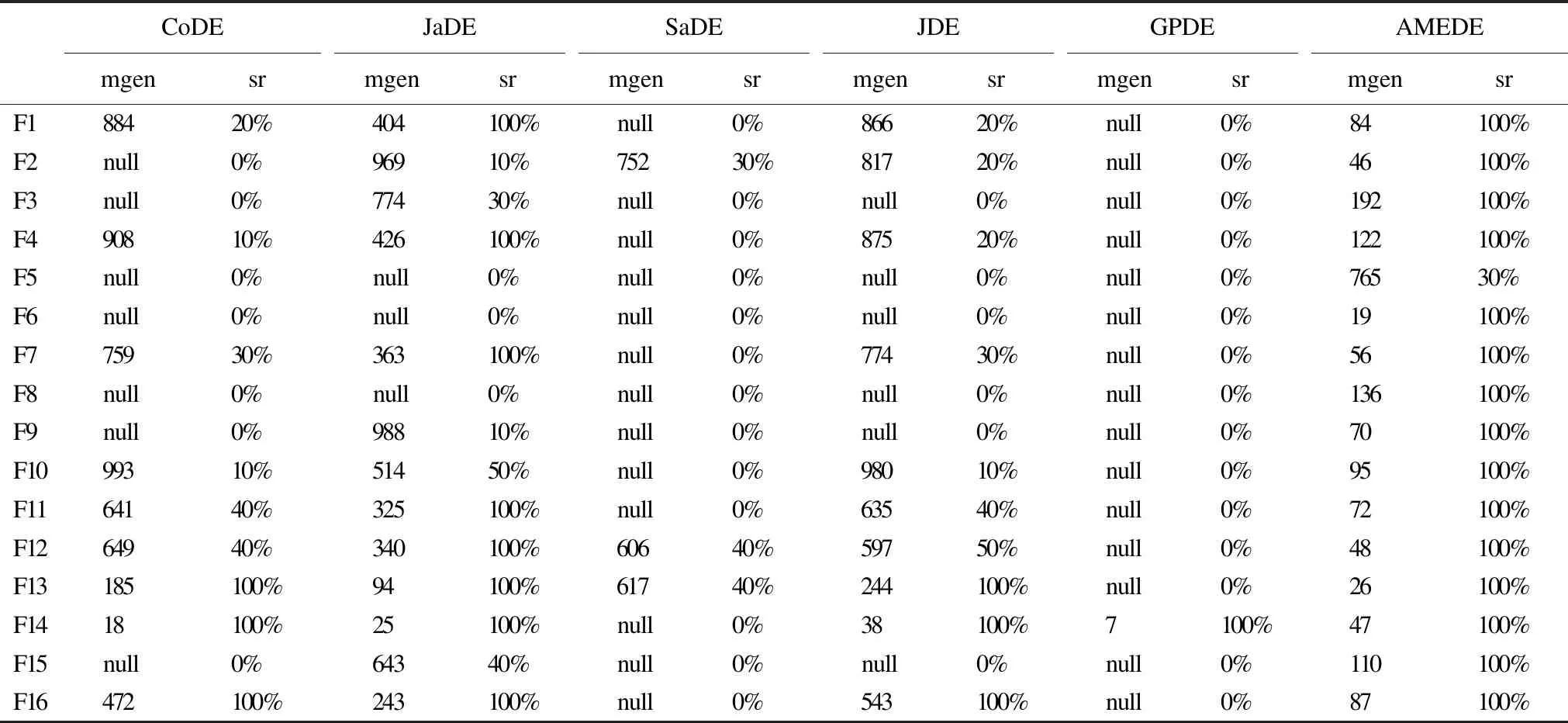
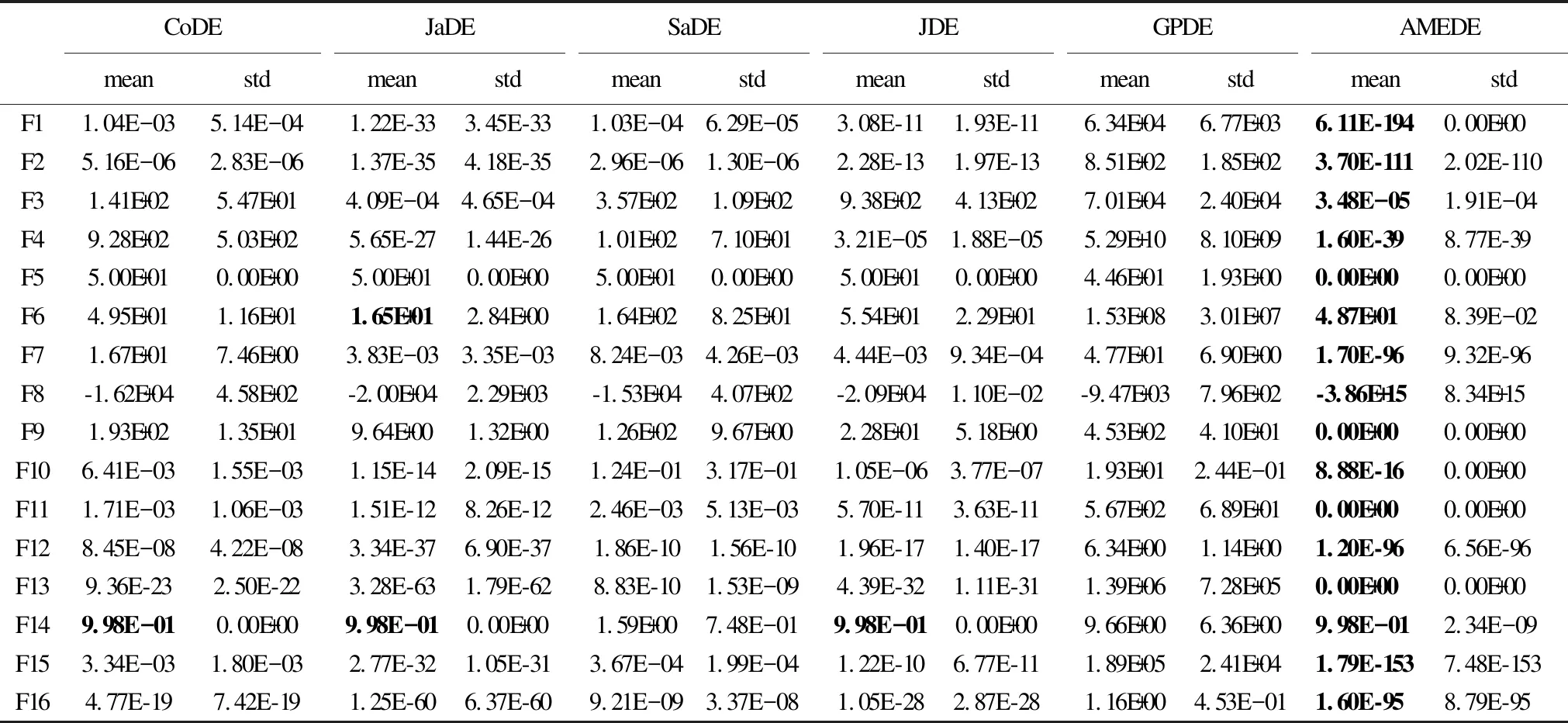
Step 3.while(i Step 4.Fort=1:NP Step 5. 评价个体适应度值fitness(X) Step 6. 通过公式(11)求解排名前五的精英个体控制参数eliteF、eliteCR和eliteω Step 7. End for Step 8. 按公式(10)求出精英个体的位置,并更新精英个体位置eliteX Step 9. 按公式(15)概率阈值公式选择自适应参数操作 Step 10.p=rand(0,1); Step 11. Ifp<τ Step 12. 按公式(12)更新CPi参数; Step 13. Else Step 14. 按公式(13)更新控制参数CPi; Step 15. End if Step 16. 按公式(9)执行“DE/rand-to-eliteX/1”变异操作,生成变异个体Vi Step 17. 按公式(7)执行交叉操作生成新的候选个体 Step 18. 计算新的候选个体适应度值,并更新初始种群个体 Step 19.Fort=1:NP Step 20. If fitness(Xi) Step 21.X(i)=U(i); Step 22. fitness(Xi)=fitness(Ui); Step 23. End if Step 24. End for Step 25. 更新初始种群个体后,按照公式(10)更新精英个体位置 Step 26. 更新初始种群个体后,按照公式(11)更新精英个体控制参数值 Step 27. i++; Step 28. END while; 3.3.2 AMEDE算法流程图 AMEDE算法流程图如图5所示. AMEDE时间复杂度分析如下,考虑在一次迭代中最坏情况下的时间复杂度: 1)初始化种群中的时间复杂度为O(NP); 2)在求解和更新精英个体位置的时间复杂度为O(NP); 3)在不考虑适应度函数的计算成本,则评价个体适应度的时间复杂度为O(NP*D); 4)在执行参数自适应策略时,需要更新eliteF、eliteCR和eliteω,产生的时间复杂O(NP*D); 综上,可以得出AMEDE算法复杂度为O(NP*D),与标准差分进化算法时间复杂度O(Popsize*D)相比,AMEDE算法在变异策略、参数自适应选择策略阶段产生额外的计算量,但并没有明显增加算法时间复杂度. 为了验证AMEDE算法的优化性能,本文选取了16个测试基准函数.具体16个测试基准函数的表达式、取值范围和属性详见表1所示.在这个16个测试基准函数当中,F1~F5为单峰函数,主要用于评估收敛精度和收敛速度.F6~F16为多峰函数,主要是用于评估全局搜索能力.为了保证实验结果的真实可靠,实验中所有算法在相同参数设置下分别在测试基准函数独立运行30次,函数最大评估测试为1000次.采用全局最优值的平均值和标准差作为实验结果的主要分析依据.具体实验环境和实验参数设置如下: 表1 基准测试函数 1)实验环境: 采用Linux系统中的MATALAB.R2020运行所有程序. 2)实验参数设置如表2所示. 表2 实验参数设置 4.2.1 AMEDE与标准DE比较分析 将本文提出的AMEDE算法与标准差分进化(DE)算法进行对比,标准差分进化算法中包含5个变异策略,分别是“DE/best/1”、“DE/rand/1”、“DE/rand-to-best/1”、“DE/best/2”和“DE/rand/2”.实验中,根据文献[18],设置差分算法的控制参数为:种群大小(NP=100),放缩率因子(F=0.5),交叉率因子(CR=0.3).每种算法对每个函数得到的最优解均值(mean)和标准差(std)如表3、表4所示,其中最优值用粗体表示.每种算法的成功率(sr)和每个函数达到指定收敛精度所需的平均迭代次数(mgen)在表5中所示,其中“null”表示不适用.收敛精度设置:F8为-10+5为F5、F14和F16为10-1,F2和F9为10-5,F1、F7、F11、F12和F15为10-15,其他均为10-10.mgen和sr分别用于比较各算法的收敛速度和可靠性.为了便于说明,将函数的收敛曲线绘制在图4中. 表3 6种策略的测试结果(D=30) 表4 6种策略的测试结果(D=50) 表5 6种策略的稳定性测试结果(D=30) 图4 F1-F16收敛图 算法结果分析如下: 从实验结果中可以看出,AMEDE算法在D=30和D=50的情况下,都能够在所有的基准测试函数上找到最优值,且收敛速度快,稳定性强.当D=30时,AMEDE算法仅在测试基准函数F14上没有找到比“DE/rand/1”、“DE/rand-to-best/1”和“DE/rand/2”更小的最优值,但AMEDE算法也取得了不错的最优值结果.AMEDE算法能在16个测试基准函数中能获取到5个基准测试函数(F5、F9、F11、F13和F16)的全局最优值,另外在13个基准测试函数上优于“DE/rand/2”,在15个基准测试函数上优于“DE/rand/1”和在16个基准测试函数优于“DE/best/1”、“DE/rand-to-best/1”和“DE/best/2”.当D=50时,AMEDE算法仍能够在基准测试函数F5、F9、F11和F13上获取到全局最优值,除在F14上没有明显优于其他变异策略以外,在其他的基准测试函数上都获取到了最优值.这说明AMEDE算法在高维基准问题下,仍能够保持一个较好的寻优能力. 具体的从表4和图4中可知,收敛精度和收敛速度方面,AMEDE是5种变异策略中表现最好的.这是因为AMEDE通过改进“DE/rand/1”模式和引入控制参数自适应策略,可以动态调整种群多样性,提高收敛性能.从表5中可知,在可靠性方面,标准DE性能明显不如AMEDE算法.对于标差分进化算法中的变异策略来说,使用固定的参数设置并不适合各种基准测试函数.例如,“DE/rand/2”和“DE/best/1”在单峰函数F1和F2上得到了较好的结果,而在多峰函数F7、F8和F11上结果较差. 对标准差分进化算法中的各个变异策略方法和AMEDE算法在各基准测试函数上的最优结果的均值排名采用Friedman检验,结果如表6所示,均值排名为算法在各基准测试函数上排名的均值,并且分为所有基准测试函数、单峰基准测试函数、多峰基准测试函数3种情况进行分析,卡方值为对应的统计值,P值为对应的概率值,如果P<0.05则可以说明,在0.05水平上对应情况上6种变异策略方法有明显差异显著,而排名情况也能说明各个变异策略算法的优劣.从表5中可以得出,在所有的基准测试函数上p值均<0.05,并且在3种情况下AMEDE算法排名均为第一.在F检验的结果下AMEDE算法相比于标准差分进化算法中的变异策略方法有更好的寻优效果. 表6 AMEDE算法与DE算法的F检验结果 4.2.2 AMEDE与其他改进DE比较分析 将AMEDE算法与复杂差分进化算法(CoDE)[8]、自适应差分进化策略(JaDE)[19]、自适应参数差分进化算法(SaDE)[20]、带有外部归档的自适应差分进化算法(JDE)[21]和基于高斯变异和动态参数调整的差分进化算法(GPDE)[13]等5种具有代表性的改进差分进化算法进行对比. 实验中,各算法控制参数按照对应参考文献进行设置.各个算法的实验结果如表7、表8、表9和表10所示,其中全局最优值用粗体表示. 表7 6个算法的测试结果(D=30) 表8 6个算法的稳定性测试结果(D=30) 表9 6个算法的测试结果(D=50) 表10 AMEDE算法对其他算法的T检验结果 1)算法结果分析 根据实验结果可知,AMEDE算法在16个基准测试函数中寻优效果最好,能够在15个基准测试函数上获得最优值.表7和表8列出了6种差分改进算法在16个标准测试函数上独立运行30次后所出结果的平均值和标准差.从表中可以看出AMEDE算法在单峰函数F5和多峰函数F9、F11、F13和F16上收敛精度明显优于其他5个算法.AMEDE算法在多峰基准测试函数F6上最优值的收敛精度略次于SaDE算法.SaDE作为经典差分改进算法中的一员,在一些基准测试函数上有较好的收敛结果,这也是不意外的.AMEDE算法在多峰函数F14上收敛精度和稳定性略劣于CoDE、JaDE和JDE,优于SaDE和GPED算法.对于SaDE和GPED,虽然采用了参数自适应策略来提高DE的性能,但控制参数值的更新是随机的,缺乏演化过程的指导.对于GPED,在产生新的控制参数值时,没有考虑个体的差异,容易导致过早收敛.而在AMEDE中,控制参数值会根据种群多样性自动调整,并利用个体的差异来指导生成新的参数,有利于提高个体逃避局部极小值的能力,促进个体向正确方向搜索.因此,IMMSADE的性能最好.在AMEDE中,控制参数值会根据种群多样性自动调整,并利用个体的差异来指导生成新的参数,有利于提高个体逃避局部极小值的能力,促进个体向正确方向搜索.因此,IMMSADE的性能最好. 另外,采用Kruskal-Wallis检验显著性水平为5%的非参数统计检验进行多重比较.表10为AMEDE算法对其他5个算法的T检验值和检验结果.“+”、“-”、“=”分别表示AMEDE算法对比相应算法明显优于、明显劣于、差异不明显3种情况,分别用B、W、S表示.AMEDE算法对比CoDE算法、SaDE算法、JDE算法、JaDE和GPDE算法的B-W得分情况分别为14、13、16、15和16,都呈现出明显优势且没有出现明显劣于其他的5个对比算法,T检验结果表明AMEDE的性能明显优于其他的改进差分算法. 2)算法收敛性分析 图5分别是DE算法、CoDE算法、SaDE算法、JDE算法、JaDE算法和GPDE算法在16个基准测试函数上的收敛曲线,其中横坐标为迭代次数,纵坐标为函数的适应度值.为了方便对比,纵坐标经过了对数变换,仅画出了各算法在基准测试函数上的0-1000代之间的收敛曲线图.从图5中可知AMEDE算法在16个测试基准函数上的收敛速明显优于其他算法,在单峰函数上尤其明显,另外在大部分多峰函数上收敛表现也较好,这说明AMEDE算法寻优速度快且收敛精度更高,除了在基准测试函数F6上比DE算法略劣.另外,在测试函数F14上,前期收敛速度较慢但是后期也与其他算法相差甚少,AMEDE算法在大部分基准测试函数上前期的收敛速度都优于其他5个对比算法,由于精英组中的所有个体并不是全局最优个体,因此个体的位置发生改变,因此放慢了收敛速度,但是通过学习控制参数后使得算法后期加快速收敛速度.AMEDE算法在前期利用精英个体代替全局最优个体,保证了种群的多样性,并采用学习精英个体控制参数信息的方法,加快了前期的收敛速度,为了进一步确保种群中个体不发散引入的权重因子发挥了重要作用,增加了算法的收敛精度. 图5 F1-F16收敛图 4.2.3 AMEDE的变异策略和参数分析 AMEDE通过改进“DE/rand-to-best/1”变异策略和引入控制参数自适应策略来提高DE的性能.虽然,上文中的两个实验验证AMEDE性能.但却无法充分评估公式(5)所示的改进变异策略和自适应参数策略的有效性.为了解决这个问题,将不进行参数自适应的AMEDE算法和标准差分进化算法与AMEDE进行了比较.对DE中的控制参数分别设置为F=0.5,CR=0.9,对不进行参数自适应的AMEDE算法,ω=0.2,放缩率因子F=0.5,交叉率因子CR=0.9,另外AMEDE的参数设置与第一个实验相同.此外,AMEDE在参数自适应策略中引入控制参数ω,因此确定ω的取值范围对于不同的优化问题是很有意义的.表12记录了将ω分别设为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1.0得到的实验结果.其中全局最优值用粗体表示. 算法结果分析如下: 实验结果由表11可以得出,与DE相比,不带参数自适应的AMEDE性能明显更好,这是因为改进的变异模式加快了在目标的方向上的优化搜索,提高了收敛性能.此外,还可以得出,AMEDE算法最好,无参数自适应的AMEDE算法次之,DE最差.这表明改进的突变模式是有效的.与无参数自适应的AMEDE算法相比,AMEDE在收敛精度和收敛速度方面都有更好的表现.这表明改进的突变策略与参数适应策略是一种有益的配合.在参数自适应策略中为控制参数自适应到合适的值,从而提高了算法的收敛性能.从表中还能看出,在D=30时,没有进行参数自适应的AMEDE算法,F3、F12和F15函数上要优于AMEDE算法;在D=50时,没有进行参数自适应的AMEDE算法,F3和F12函数上要优于AMEDE算法.这可能是由于AMEDE算法进行控制参数适应策略,在进化后期,由于种群多样性降低,可能需要频繁调整参数值.但这些参数值可能不利于算法在有限的进化生成数内收敛,从而导致最终解的精度较低.此外,解决在高维度问题时参数的适应性也进一步提高了F6、F9、F13和F15函数的收敛精度.参数自适应策略还可以帮助算法在求解具有多个局部极小值的函数时,寻找更好的解,并保持较高的收敛速度. 表11 不进行参数适应的AMEDE与AMEDE对比(D=30、50) 如表12所示,ω取值为ω≥0.6时,AMEDE表现较差.ω值越大,控制参数的更新速率越高,不利于新个体的产生和种群多样性的维持.种群多样性的降低导致早熟收敛,从而降低了收敛精度和收敛速度.相反,AMEDE设置ω≤0.5时,性能更好.ω值越小,越有利于调整种群多样性,从而提高全球勘探能力.因此,当参数ω∈[0.1,0.6]时,AMEDE的性能最佳. 表12 AMEDE的不同参数实验结果 通过以上实证分析,可以得出,所提出的AMEDE具有更快的收敛速度、更高的收敛精度和更强的鲁棒性,满足了过程优化的实时性、准确性和稳定性要求. 本文提出的自适应参数精英变异策略的差分进化算法主要是为了解决标准差分算法中控制参数和变异策略敏感和过早收敛的问题.AMEDE算法结合了精英变异策略、参数自适应策略和引入新的控制参数权重因子.精英变异策略利用种群中优秀个体的信息来引导种群中其他个体,保证了算法的搜索效率;参数自适应策略中的全体学习法,通过学习种群中精英个体的控制参数并对其他个体控制参数进行动态调整,从而有效地避免了早熟收敛;通过概率阈值来选择合适的参数自适应策略,保证了种群的多样性和收敛速度;新的控制参数权重因子是为了让个体不再发散,确保个体收敛.通过16个测试基准函数和3个对比实验的结果表明,本文提出的AMEDE算法具有更快的收敛速度、更高的收敛精度和更强的鲁棒性,能够满足过程优化的实时性、准确性和稳定性要求. 未来还继续在自适应参数和变异策略上再进一步研究,提出不同的变异策略和不同的自适应参数方法来提升算法性能.3.4 AMEDE 算法复杂度分析
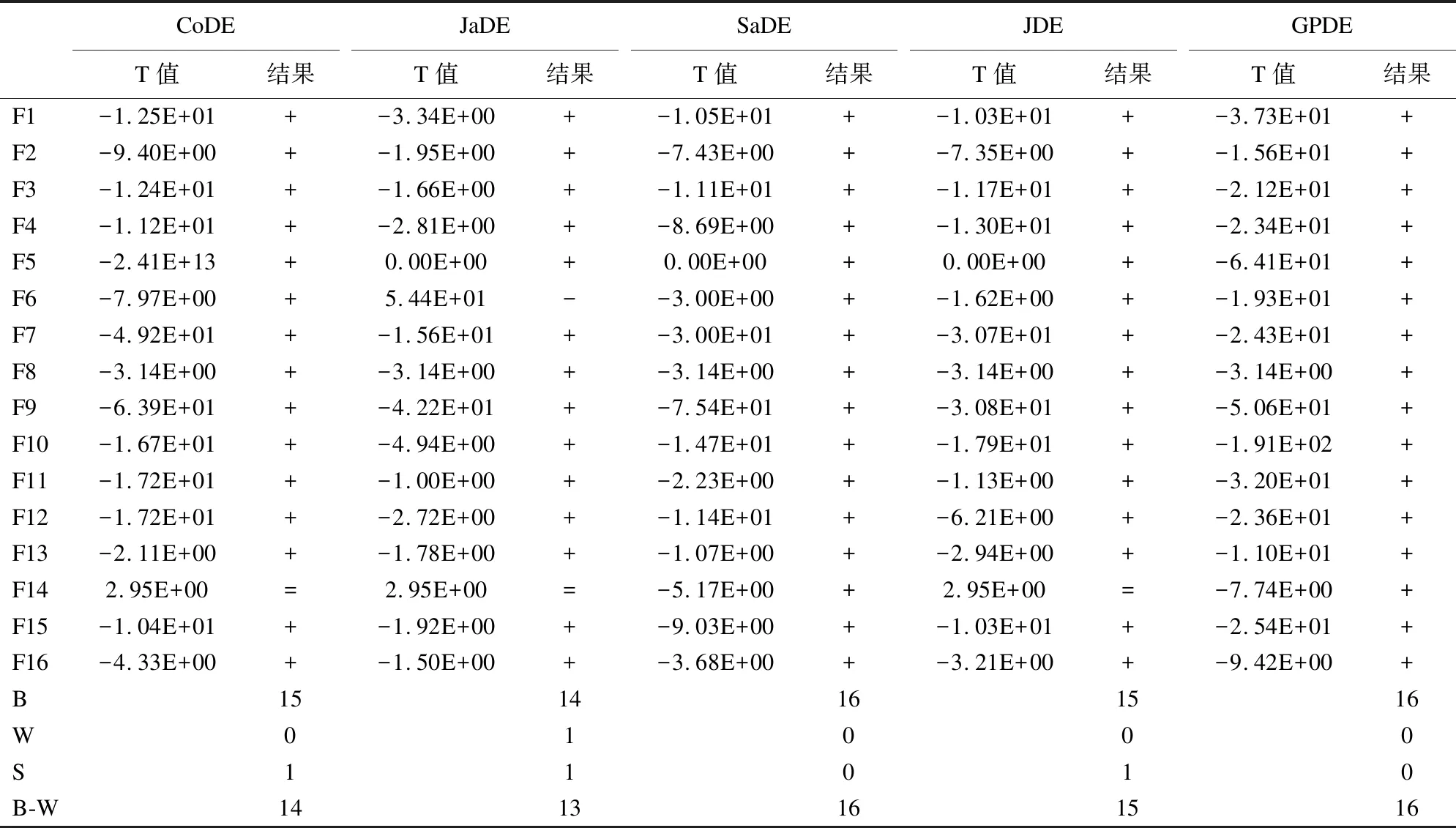
4 实验与结果分析
4.1 实验设置

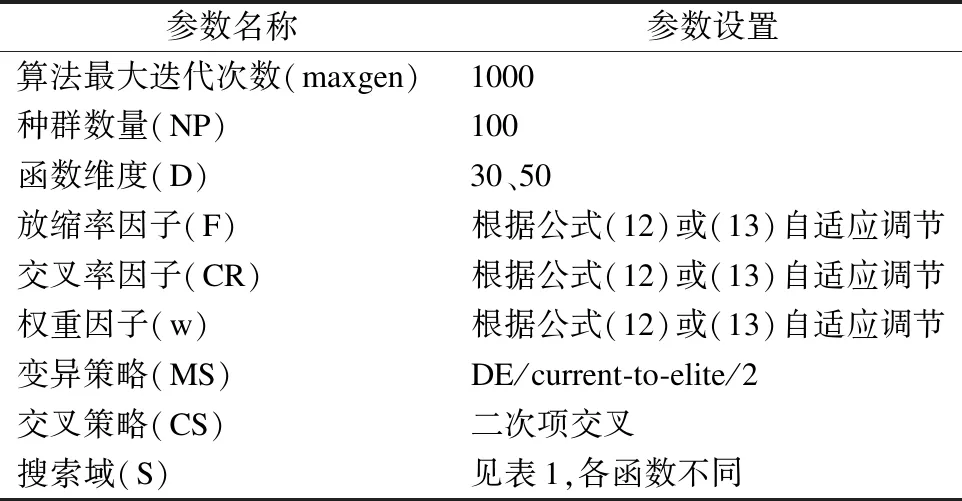
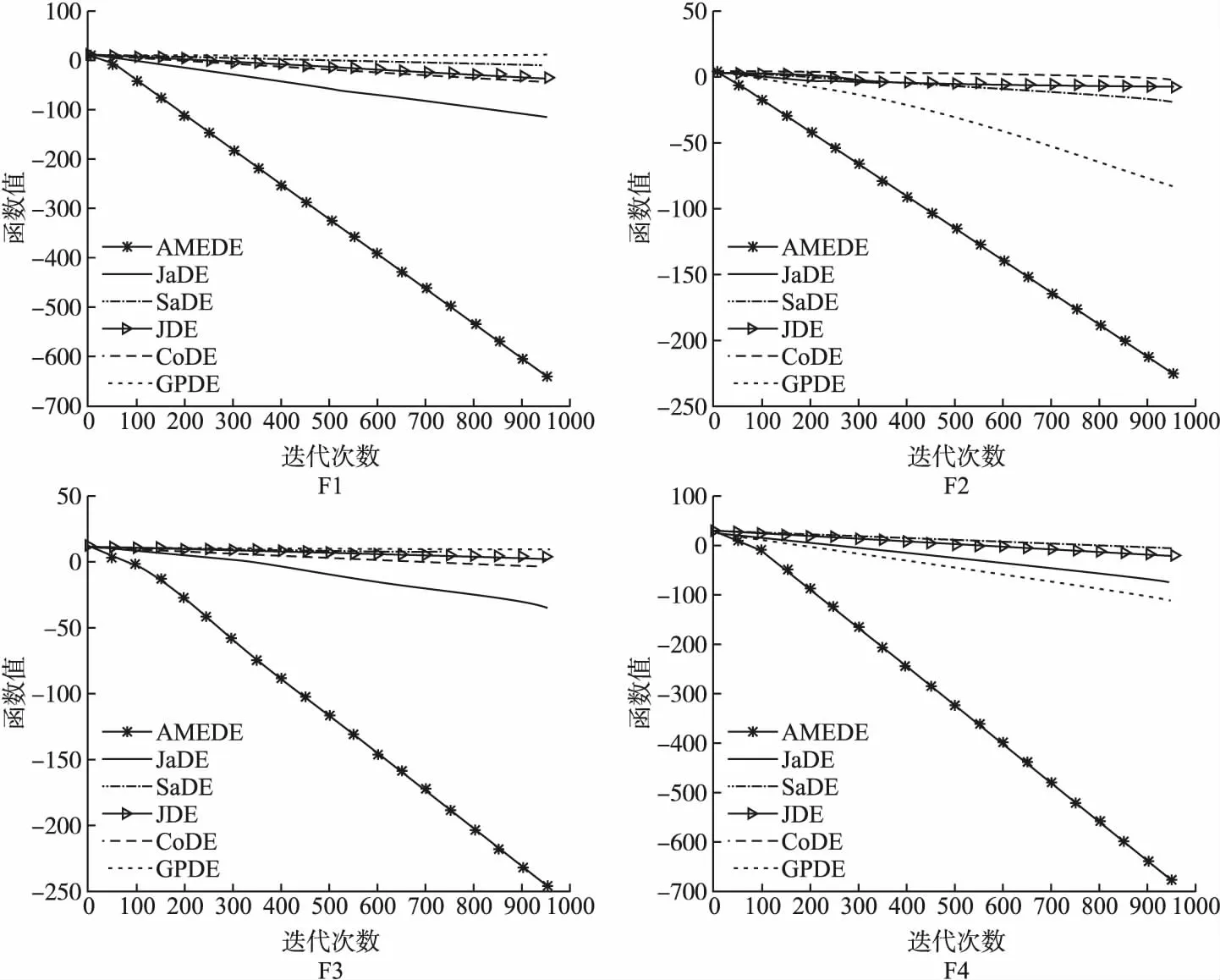
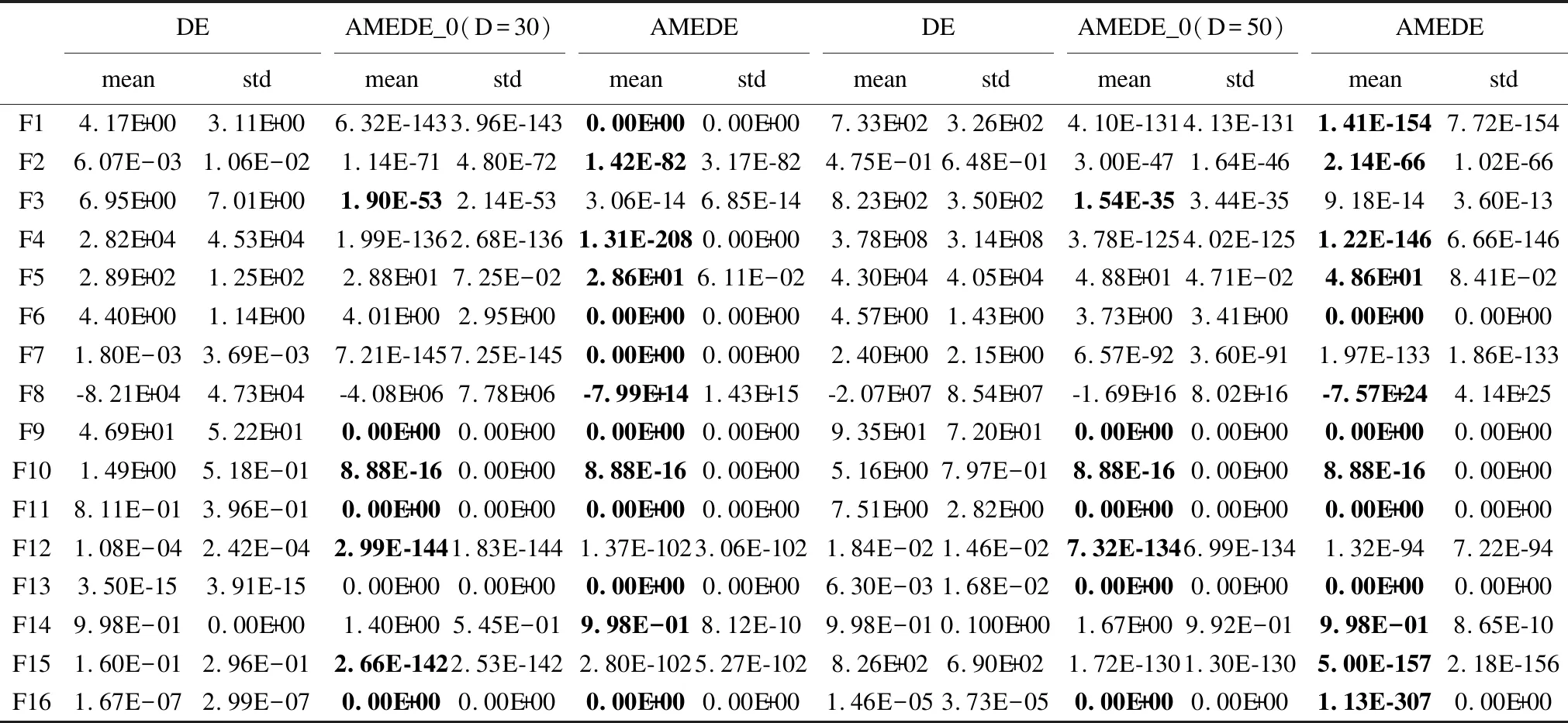
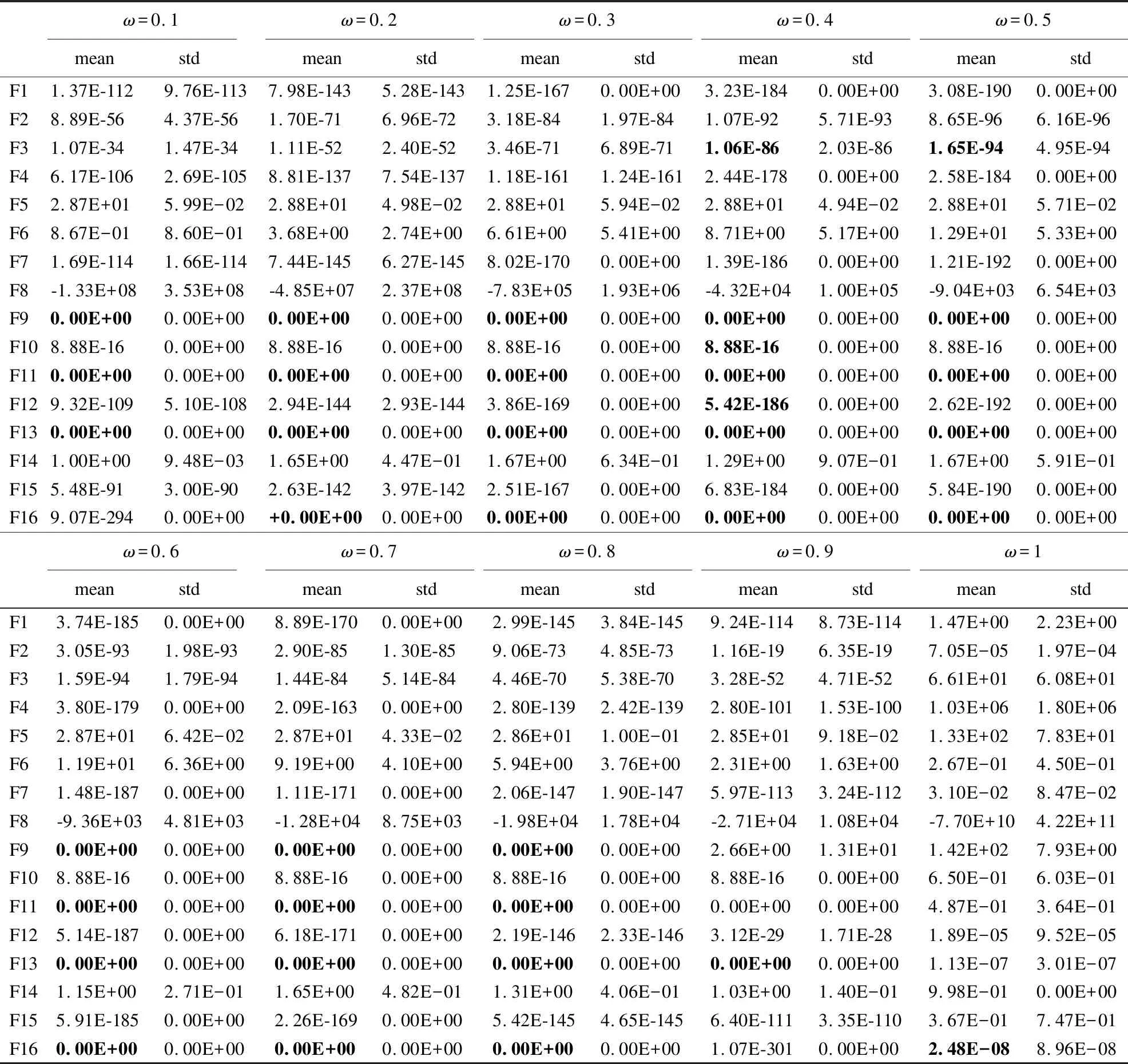
4.2 对比实验及结果分析
5 结束语

