基于互信息和叶子节点属性的因果结构学习方法

谢 峰,曾 艳

1(北京大学 概率统计系,北京 100871)

2(清华大学 计算机科学与技术系,北京 100084)

1 引 言

近年来,基于观测数据的因果结构学习研究,即因果发现(causal discovery),引起了越来越多学者的关注,并被广泛应用在神经学、经济学等领域中[1-6].传统的因果结构学习算法通常被分为两大类:基于约束的(constraint-based)算法,例如Peter Clark(PC)[7],Grow-Shrink(GS)[8],Fast Causal Inference(FCI)[9],Really Fast Causal Inference(RFCI)[10]和Iterative Causal Discovery(ICD)[11]算法,和基于评分的算法,例如Greedy Equivalence Search(GES)[12],Fast Greedy Equivalence Search(FGES)[13],GOBNILP-DEV[14]等算法.然而,上述多数方法输出的因果结构属于马尔科夫等价类,即它们不能够找到唯一一个完整的有向无环图(Directed Acyclic Graph,DAG)[15].

在线性系统下,为了解决因果结构唯一性的问题,Shimizu等人[16,17]提出了线性非高斯无环模型(Linear Non-Gaussian Acyclic Models,LiNGAM).相较于传统的方法相比,该模型引入了非高斯性的假设从而能够有效区分马尔科夫等价类而获得唯一的因果网络.针对LiNGAM模型的估计方法包含了基于独立成分分析(Independent Component Analysis,ICA)的ICA-LiNGAM算法[16],基于独立性的直接估计因果次序的DirectLiNGAM算法[18],其改进版本成对比较的Pairwise-LiNGAM算法[19]等.之后Xie等人[20]利用信息熵的方式,提出了两阶段迭代的Entropy-based Two-Phase Iterative Algorithm(EPTIA)算法,来估计LiNGAM模型.除此之外,研究学者从不同的角度对该模型进行改进分析:含隐变量的LiNGAM模型,如基于完备ICA的方法[21,22],RCD算法[23]等;时序数据的SVAR(Structural Vector Auto Regression)模型,如基于改进LiNGLAM似然的方法[24],基于不等约束的方法[25]和基于广义矩估计的方法[26];非线性的ANM模型[27,28];隐变量/因子(Latent Variables/Factors)的因果结构学习[29,30];以及从评分的角度,提出改进的似然函数进行评分,从而学习因果结构,如Structural Equational Embedded Likelihood(SELF)[31]和Notears[32]算法等.

然而,上述的算法在学习无隐变量的结构时,大多数通常是以自顶向下的方式来估计因果次序,再学习因果结构.也就是说,它们通过优先选择根节点的方式来确定因果次序[18-20].这种自顶向下的估计方式会存在如下问题:在迭代确定因果次序的过程中,每次选择完一个根节点后,它们都需要不断地更新原始数据,从而引入额外的误差使得算法的识别准确率降低[33].特别地来说,当数据的维度越高时,这个问题带来的影响则会越明显.为了解决这个问题,近来,Zeng等人[33]采取自底向上的方式来识别因果次序,并提出了优先选择叶子节点的算法(Giving Priority of Leaf Nodes,GPL).尽管文献[33]提供了完整的理论和证明了GPL算法的准确性,但是其理论和证明需要满足一个额外的假设,即数据背后真实的因果结构满足因果树假设.因果树结构是一类特殊的DAG,并具有以下性质:因果树中的任意两个节点有且仅有1条路径.当数据本身不满足因果树假设时,GPL算法便会输出不可靠的因果网络.

因此,针对以上所述问题,本文提出了一种基于叶节点性质和互信息的因果结构估计方法(Causal Structure estimate method based on Leaf and Mutual information),并简写为CSLM.具体来说,考虑到非因果树结构下,任意两个变量间可能存在混淆因子,为此本文利用变量与残差间的独立性去识别是否存在混淆因子,若存在需要剔除该混淆因子的因果影响;此外考虑到叶子节点在因果网络中是一种特殊的节点,即该节点不会影响剩余任意节点,基于互信息的方式去度量变量间的独立性从而找到独立性最小的节点即为叶子节点.本文的主要贡献总结如下:

1)提出了一种新的估计LiNGLAM的CSLM方法.该CSLM算法以自底向上的方式估计因果次序.与经典的自顶向下的算法相比,CSLM在数据维度较大的情况下具有更高的识别准确率;

2)解决了自底向上的方法需要假设网络为因果树的形式,使得算法更加通用且更符合实际场景;

3)在虚拟网络和真实网络数据集上进行结构学习,与最新的方法相比,证明了CSLM算法的有效性.

2 预备知识

LiNGAM模型是由Shimizu等人[16,17]首次提出,该模型因其能够打破传统的马尔可夫等价类,从而能够识别变量间的因果方法而得到广泛关注.LiNGAM模型的基本设定是:变量间的因果生成机制满足线性结构方程模型,不失一般性,假定变量的均值为0,那么可以表达为如下形式:

(1)

其中,i={1,…,n},xi表示可观测变量;bij表示DAG中变量xj到xi的连接强度;ei表示噪声变量,服从非零方差的非高斯分布,且彼此间相互独立;K(i)表示变量xi的整个网络中的因果次序.

当数据满足以下3个基本的假设:1)数据产生过程满足公式(1),即线性假设;2)因果充分性假设,即不存在隐藏变量;3)噪声变量ei服从非零方差的非高斯分布.那么该模型为LiNGAM模型.将式(1)写成矩阵的形式如下:

X=BX+e

(2)

其中X=[x1,…,xn]T,e=[e1,…,en]T,连接矩阵B存储了变量与变量之间的连接强度bij.

如考虑如图1中所示因果结构,其因果生成机制可以表达为如下形式:

图1 数据生成机制满足LiNGLAM的示例

其中因果次序K=[1,2,3,4].

本文的目标是如何有效地估计LiNGAM模型,尤其是高维网络.具体来讲,在给定观察数据X的情况下,求解因果次序K和连接矩阵B,进而学习完整的因果结构.

3 基于叶节点性质和互信息的因果结构学习

为了使得算法能有效处理高维数据,文献[33]提出了通过自底向上的GPL算法,该方法巧妙地避开了传统的自顶向下学习策略中需要迭代更新数据集带来的级联错误,提高了高维网络下因果网络估计效果.不幸的是,除了LiNGAM模型的基本假设以外,该方法需要引入额外地假设,即背后的因果网络是因果树(任意两个节点有且仅有1条路径).尽管有些时候可以由专家经验知识支撑该假设,但是在多数情况下,该假设的引入导致了该方法无法解决非树模型的局限性.

在本章节中,首先在2.1小节中,通过一个简单的例子,说明因果树假设带来的估计问题,以及解决的方法.紧接着,在2.2小节中,会给出相应的理论保证.最后,本文在2.3小节中,描述了基于叶节点性质和互信息的因果结构学习框架,该框架下不需要因果树假设的引入,解决范围更加广泛.

3.1 直观示例

接下来,考虑如图2所示的因果网络.

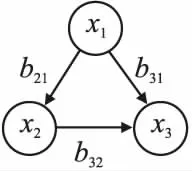
图2 一个具有3个节点的因果结构

图2所示的结构是一个具有3个节点的因果网络.由于节点x1到节点x3有2条路径,显然该结构不满足因果树假设.从独立性的角度出发,可以发现:

对于节点x1,有:

x1⊥x2-E(x2|x1)&x1⊥x3-E(x3|x1)

然而对于节点x2,有:

x2⊥/x1-E(x1|x2)&x2⊥/x3-E(x3|x2)

同时对于节点x3,有:

x3⊥/x1-E(x1|x3)&x3⊥/x2-E(x2|x3)

由文献[33]的理论可知,在因果树假设成立的条件下,叶子节点具有独立性最弱的性质,即叶子节点xj均不独立于与其余变量分别做回归的所有残差xj-E(xi|xj),i≠j.所以,在图2不满足因果树假设的结构中,节点x2和节点x3与其余变量对应的残差都不独立.如果使用GPL算法来学习因果次序,则有可能会将节点x2作为叶子节点输出.然而,x2并不是叶子节点.因此,如果数据不满足因果树假设,GPL算法的理论便会出现问题,且算法的识别准确率会降低.其本质原因在于x1是x2和x3间的混淆因子,影响了成对变量独立性测试的结果.

为此,如果想解决非因果树的结果,即去除该假设,为此需要提前确定任意两个变量间是否含有混淆因子,如果含有,需要提前局部地剔除该变量对其余变量的影响,从而避开混淆因子带来的影响.例如重新考虑上述例子,发现x2和x3都可能是叶子节点,这个时候,如果同时给定变量x1变量后,会帮助找到x3是叶子节点,即:

x2⊥/x2-E(x2|x1,x3)&x3⊥x3-E(x3|x1,x2)

总结来说,为了让算法更广泛,需要测试变量间的混淆因子并剔除该混淆因子的影响,从而自底向上的学习整个网络.

3.2 理论分析

为了解决混淆因子所引起的因果树假设问题,需要利用混淆因子的性质来识别它们,并去除掉混淆因子对其余节点的影响.

首先给出了混淆因子的性质.在此之前,需要给出一个刻画非高斯数据集独立性的重要定理.

[D-S定理[34]]给定两个随机变量x1和x2是由独立的随机变量线性组合而成,即:

那么,如果存在独立随机变量ei服从非高斯分布且λiγy≠0,那么随机变量x1和x2是统计依赖的.

定理1. 假设观察数据集X满足LiNGAM模型,当且仅当xi与xj之间存在混淆因子时,xi⊥/xi-E(xi|xj)和xj⊥/xj-E(xj|xi)成立.

证明:定理1的证明,需要从充分性与必要性两方面来证明.

首先考虑充分性.因为条件xi⊥/xi-E(xi|xj)和xj⊥/xj-E(xj|xi)都成立,那么变量xi与xj之间一定不独立.根据D-S定理,得到变量xi与xj间一定含有至少一个相同的噪声项,假设为ek.根据线性模型的假设,得到一定至少存在一个变量包含噪声ek且同时指向变量xi与xj,由此可知,xi与xj之间存在混淆因子.

现在考虑xi与xj之间存在混淆因子的情况.假设该混淆因子为xk.那么根据线性回归公式,残差xi-E(xi|xj)和xj-E(xj|xi)一定含有xk的噪声项exk.根据D-S定理,能够得到xi⊥/xi-E(xi|xj)和xj⊥/xj-E(xj|xi)成立.

定理1证明完毕!

由定理1可知,给定任意两个节点xi与xj,如果xi不独立于xi-E(xi|xj),且xj不独立于xj-E(xj|xi),则说明这两个节点之间至少存在一个混淆因子.此时,只需要在其余所有节点上依次对xi与xj做回归,即可将混淆因子对节点xi与xj的影响去除,因为在非混淆因子上做回归对原有节点与残差之间的独立性是没有影响的.根据定理1,可以推断出叶子节点的性质.

定理2. 假设观察数据集X满足LiNGAM模型,那么,对于变量xi和其余任意相关的变量xj,j≠i,不存在一个子集S∈X满足xj⊥xj-E(xj|xi,S),那么xi为叶子节点.换句话说,当xi与其余所有的残差都不独立时,xi为叶子节点.

证明:从文献[30]中的命题1可得,在给定某个变量,如xi的所有父节点Pa(xi)时,xi⊥xi-E(xi|Pa(xi)),而给定其后代节点时,xi⊥/xi-E(xi|Des(xi)).因为叶子节点的性质,没有后代节点,那么不会存在后者的情况,即xi与其余所有的残差都会不独立.因此xi为叶子节点.证毕!

定理2描述了叶子节点独立性最弱的性质.值得注意的是,该定理无需假设数据是由因果树生成的.

3.3 CSLM算法

根据2.2小节中的理论分析,本小节将介绍一种基于叶节点性质和互信息的因果结构估计方法,即CSLM.其基本框架为:

第1步.首先成对地计算每一个节点与其余任意节点做回归后的每一个残差之间的独立性;考虑到连续数据的独立性衡量,实际中采用核互信的方法衡量两个变量z1和z2的独立性[35].具体来说,例如z1和z2的互信息可以表示为如下形式:

第2步.紧接着根据这成对的节点是否都与残差独立,来判断是否存在混淆因子,一旦存在混淆因子,即xi⊥/xi-E(xi|xj)和xj⊥/xj-E(xj|xi)成立,则去除混淆因子对这对节点的影响;

第3步.根据独立性强弱(核互信息的大小)以自底向上的方式确定因果次序;

第4步.最后,通过剪枝步骤,如基于Lasso的最小二乘回归法,获得最终的因果结构.

该算法的伪代码详细流程如下:

算法1.CSLM算法

输入:数据集X

输出:因果次序K和连接矩阵B

1.标准化处理数据集X并初始化独立性矩阵M为零矩阵,因果次序K为空集,变量下标集合U为空集;

2.Repeat:

3. 计算xi与xi-E(xi|xj)、xj与xj-E(xj|xi)的核互信息,用于衡量之间的独立性,并分别存储在Mij与Mji中;

4. ifxi不独立于xi-E(xi|xj),且xj不独立于xj-E(xj|xi)://寻找混淆因子;

5. Repeat:

6. 在xk,k≠i,j上分别对xi与xj做回归;

7. Untilxi不独立于xi-E(xi|xj)且xj不独立于xj-E(xj|xi)不成立;//去除混淆因子对节点xi与xj的影响;

8. 重新计算xi与xi-E(xi|xj)、xj与xj-E(xj|xi)的核互信息,并存储在矩阵Mij与Mji中;

9.Until 所有的成对变量都已考虑;

10.Repeat:

11. 通过公式(3),寻找独立性最弱的变量xm作为叶子节点:

(3)

12. 将m加入到K中;

13.Until 所有节点的下标都已加入到K中;

14.输入X与K,使用基于Lasso的最小二乘回归法对因果结构进行剪枝,并输出连接矩阵B.

复杂度分析:这里分析算法主体两个部分的复杂度.令n为网络的节点个数,m为样本量,P为整个网络中最大父节点的个数.那么在算法的第1步中需要遍历任意一个变量与其余所有变量的核互信息,因此复杂度为O(mn3M2+n4M3),其中M≪m为核独立性中利用低秩分解找到的最大秩.在第2步骤中,对于任意一个变量,如果其父节点大于等于1个时,需要找到其混淆节点,因此其复杂度为O(Pmn3).注意到该过程依赖于父节点的最大值P,网络越稀疏,那么其复杂度会越低.最坏的情况,假定网络是全连接图,此时算法复杂度将达到O(mn4).在实际中,由于大多数网络往往是稀疏的,因此运行中不会达到n的4次幂.

4 实现与结果分析

为了验证本文提出算法的有效性,本文使用了虚拟结构数据集和真实结构数据集进行实验.具体来说,在4.1小节中,使用了虚拟结构数据集并选取了最新的GPL算法[33]进行实验对比.GPL算法与本文算法都是以自底向上的方式来学习因果结构,但不同的是,GPL算法需要假设数据是服从因果树假设的.因此,在这一小节中,通过改变因果树假设的违背程度,来分析和比较当假设违背时各个算法的结果.此外,在因果树假设完全违背的情况下,也分析了算法受样本量大小的影响.在4.2小节中,本文从贝叶斯网络存储库中选择了4种不同领域下的真实结构来进行实验,并选取了主流的GPL算法[33]与ETPIA算法[20]进行实验对比.与GPL和本文算法不同的是,ETPIA算法通过自顶向下的方式来学习因果结构.所以,3.2小节的目的是为了验证本文算法通过自底向上的方式来学习因果结构的有效性.

此外,针对衡量标准,本文选择了贝叶斯因果网络的常用指标召回率、准确率和F1得分.F1得分反映了因果网络结构的总体估计优劣,具体为:

召回率=TP/(TP+FN)

准确率=TP/(TP+FP)

其中,TP表示正确估计的边的个数;FP表示未估计到的边的个数;FN表示错误估计的边的个数.结果取20次独立实验的平均值.

4.1 仿真结构数据

为了验证本算法在不满足因果树假设情况下的有效性,本小节主要进行了因果树假设不同违背程度下的仿真实验.首先选取仿真因果结构的维度大小,通过改变因果结构的平均入度,来设置因果树假设违背的不同程度,从而设计对应的控制变量实验.具体地说,设置仿真因果结构的维度为{6,8,10,12,15},根据不同的平均入度{1,1.5,2,2.5}随机产生相对应的因果骨架.根据因果骨架与LiNGAM模型,随机产生样本量为{100,500,1000,2000}的实验数据.其中,加粗的数值表示在各个控制实验中的默认数值.

图3(a)、图3(c)、图3(e)展示了不同平均入度下的仿真控制实验结果.平均入度的数值越大,意味着越违背因果树假设.当仿真结构的平均入度数较小时,即因果树假设的违背程度不明显时,GPL算法与本文的算法都取得了令人满意的结果.但是,随着仿真结构的平均入度数增大,GPL算法的性能下降明显,而本文算法对平均入度相对不敏感,这是因为本文的算法不需要做因果树的假设.本文的算法始终优于对比算法,这验证了CSLM算法在不同平均入度下的有效性.图3(b)、图3(d)、图3(f)显示了不同样本量下的仿真控制实验结果.从整体来看,在因果树假设完全违背的控制条件下,随着样本量的不断增加,两种算法的性能也不断提高.但对比算法的结果却提高不明显,这是由于GPL算法受制于因果树假设.而本文算法不需要做该假设,所以效果更优于GPL.

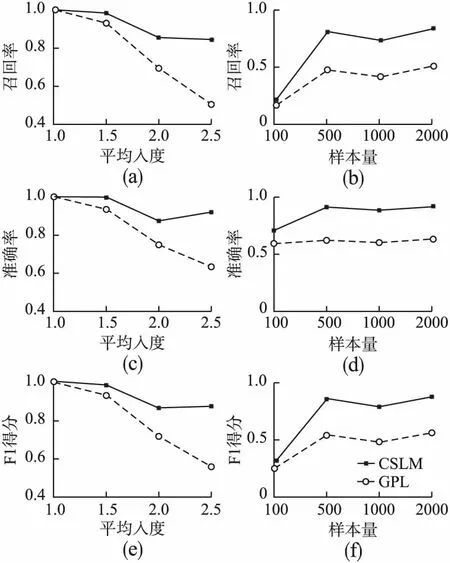
图3 不同平均入度与不同样本量下的仿真实验结果

图4展示了不同维度下的仿真实验结果.当因果结构的维度增大时,算法的F1得分都呈现下降的趋势.这是正常的现象,因为当固定样本量与最大平均入度时,维度的增大意味着结构变得更加复杂且需要的样本量本应更多(但样本量被固定),所以导致了算法学习能力的下降.尽管算法的效果不理想,但本文的CSLM算法始终至少是优于对比算法的,因此体现了本文算法的有效性.

图4 不同维度下的仿真控制实验结果

图5 不同真实结构与不同样本量下的召回率

4.2 真实结构数据

在本节中,为了说明自底向上学习方式的有效性,本文从贝叶斯网络存储库中选择了6种不同领域下的真实网络结构来进行实验,相应的公开数据链接为https://www.bnlearn.com/bnrepository/.6种真实结构的主要统计信息如表1所示.

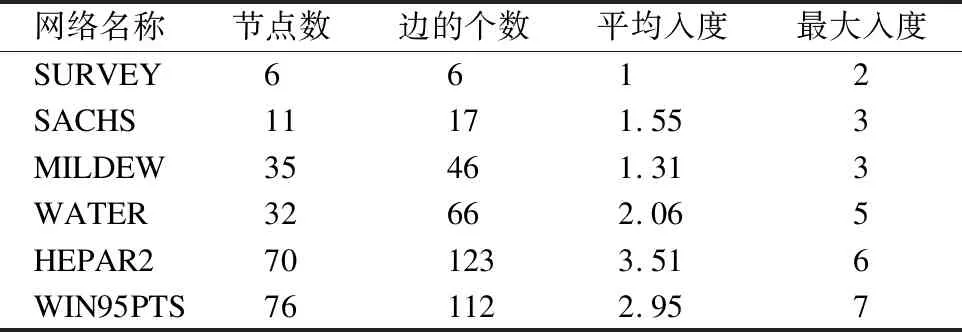
表1 真实结构的统计信息

此处设计了不同样本量{100,500,1000,2000}的对比实验.对比方法包含了GPL算法[33]与ETPIA算法[20].实验结果在图4～图6中展示.

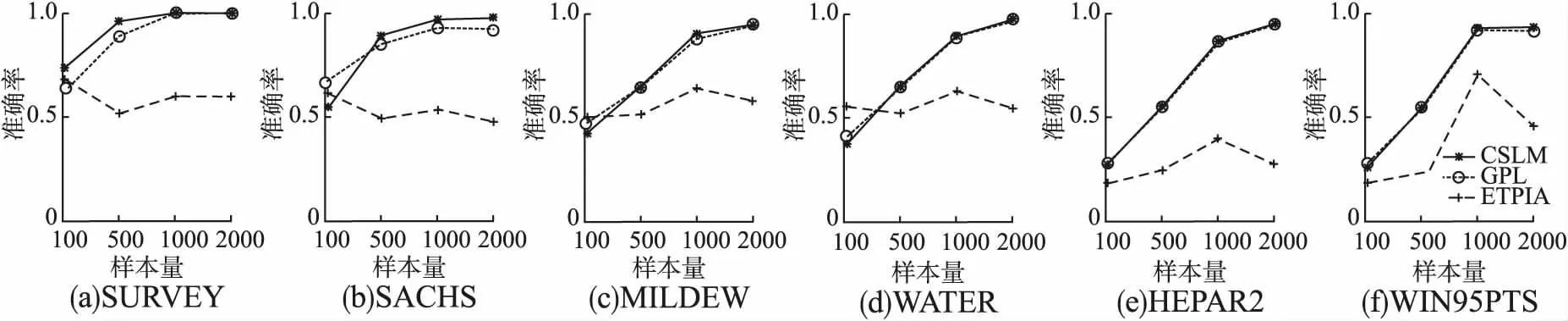
图6 不同真实结构与不同样本量下的准确率

由图5～图7所示,本文的CSLM算法和GPL算法在大多数情况下都是优于EPTIA,这得益于CSLM和GPL算法都是通过自底向上的方式来学习因果结构的,由此也说明了这种学习方式的有效性.除此之外,作者还发现CSLM算法在真实结构SURVEY与SACHS上略优于GPL算法,而在维度较大的真实结构上,两者的实验效果基本持平(尽管本文算法稍稍优于),这是因为当真实结构的平均入度不是很大时时,GPL算法能保持其学习能力;而当数据维度较大时,两者算法的学习能力同时又受到了复杂结构的影响(由3.1小节的实验验证可知).

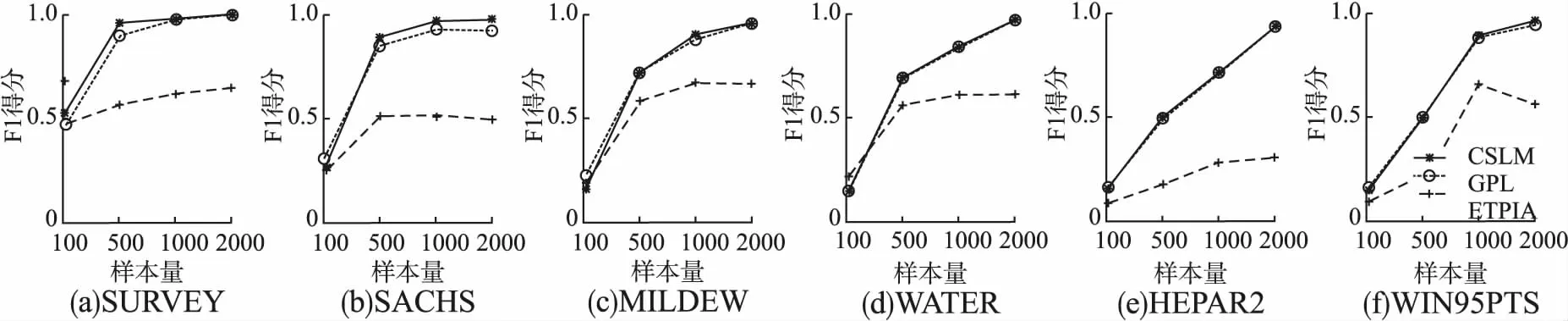
图7 不同真实结构与不同样本量下的F1得分

总的来说,从自底向上的学习方式的角度上看,本文的算法至少能保持GPL算法解决高维数据的能力,优于ETPIA算法;从是否需要做因果树假设的角度上看,本文的算法优于GPL算法,显得更加通用与有效.因此,本节验证了本文算法的稳定性与有效性.

5 结束语

本文针对现有的基于LiNGAM模型的因果结构学习算法难以有效处理高维数据且需要额外树状假设的难题,提出了一种通用的因果结构学习算法,该算法以自底向上的方式学习因果次序,且无需因果树假设.通过分析因果树假设的本质,并从混淆因子的角度去除混淆因子的影响,从而使得算法更加通用与有效.此外,实验结果验证了本文算法的优越性.下一步将考虑结构型数据下的因果结构学习.