材料断裂韧性-微观形貌-有限元仿真一体化综合实验设计
张玉财,宋 明,周 凡
(中国石油大学(华东)新能源学院,山东青岛 266580)
0 引 言
实验教学是培养学生创新思维及工程实践能力的重要途径[1],依托科研项目的科学研究型综合实验能够充分利用科研设备的优势,为实验教学改革注入新的活力。将科学研究课题与实践教学内容相结合,提高学生的创新能力、探知能力、逻辑思维能力和动手实践能力[2-3]。
断裂韧性是核电转子、油气输送管道等设备寿命预测及可靠性评价的重要参量。对于材料的断裂韧性,实验室中通常采用标准试样进行测试[4-5],需要的材料尺寸较大,难以实现服役设备性能的在线检测。纳米压痕测试需要试样的尺寸较小,对试样的形状没有特殊要求,可以方便地从在役设备上取样而不影响其正常运转,近年来得到了广泛关注。纳米压痕测试过程中,加载点的载荷位移曲线是计算断裂韧性的重要数据[6]。因此当前对于材料断裂韧性的纳米压痕测试,主要注重于加载点的载荷位移曲线等宏观现象研究。对压痕的压入过程及压痕形貌研究相对较少,忽略了压痕形貌对测试结果的影响,进而影响断裂韧性表征模型的选取及其计算精度。
针对当前常规断裂韧性测试及纳米压痕测试过程中存在的问题,依托国家级科研课题,基于材料断裂行为表征研究的部分科研成果,利用学校的纳米压痕测试仪、原子力显微镜及有限元软件ABAQUS 等科研设备和仿真软件,设计了基于纳米压痕测试-微观形貌分析-测试过程仿真还原一体化的断裂韧性综合测试实验。通过该综合性实验的开展,在制定实验方案、公式推导、实验操作及结果分析的基础上,进一步培养学生的创新意识、微观探知能力和逻辑推导能力,并掌握纳米压痕测试表征材料力学性能的分析手段,实现基于小试样“一叶知秋”的材料性能评价方法和学生动手实践能力的培养。
1 断裂韧性实验设计及方法
利用纳米压痕设备测试材料的加载点载荷位移曲线,通过加载点的载荷位移曲线计算获得材料的断裂韧性。利用原子力显微镜观测材料压痕后的形貌,为断裂韧性计算本构模型的选取提供理论依据。最后利用有限元软件ABAQUS仿真模拟压痕测试过程,再现整个测试过程中材料的变形行为,进而设计基于纳米压痕测试-微观形貌分析-测试过程仿真还原一体化的断裂韧性综合测试实验。实验测试之前,学生需掌握纳米压痕法计算断裂韧性的理论、试样制备、仪器设备操作和有限元软件使用方法,培养学生的文献检索能力、逻辑推导能力及实践动手能力。
1.1 材料及试样
纳米压痕测试实验过程中采用的材料为X80 管线钢,试样类型为20 mm ×10 mm ×3 mm(长×宽×高)的立方块。为了便于表面处理和测试,对纳米压痕测试试样进行热镶嵌。试样所在的镶嵌面经过砂纸湿磨后(砂纸由40 目逐渐打磨至2 500 目)再进行机械抛光处理(抛光膏由W3.5 逐级提升至W1.5),最后采用振动抛光机进行精磨,确保试样表面处于一个良好的状态。
对于X80 管线钢,通过电子背散射衍射(EBSD)分析可知,在材料的长度方向,材料组织较为均匀,没有出现明显的晶粒拉伸。在材料的厚度方向,材料的外周和内周都没有出现显著的非均匀性,表面和内部组织都是均匀的,如图1 所示。因此在后续的纳米压痕测试实验中,不需要特别考虑材料的不均匀性对压痕区的选取。

图1 X80管线钢微观组织晶体取向分布
1.2 断裂韧性纳米压痕测试设备及原理
实验过程中采用的纳米压痕实验设备为Nano Indenter G200 型纳米压痕仪。在测试过程中,压头类型选择Berkovich 锥形压头,型号为TB23503-XP。实验前,将试样固定于压痕仪承载平台上,如图2(a)所示,然后放入纳米压痕仪中进行测试。Nano Indenter G200 型纳米压痕仪的外观如图2(b)所示。

图2 纳米压痕实验设备与试样
图3 所示为Berkovich压头测试加载/卸载过程中的变形示意图。图中he、hp、hmax、hc、AP和Ac分别为弹性深度、压头卸载后的塑性残余深度、最大压头深度、压头最大接触深度、塑性残余投影面积和接触投影面积。卸载后压头区域留有一定的塑性残余变形。
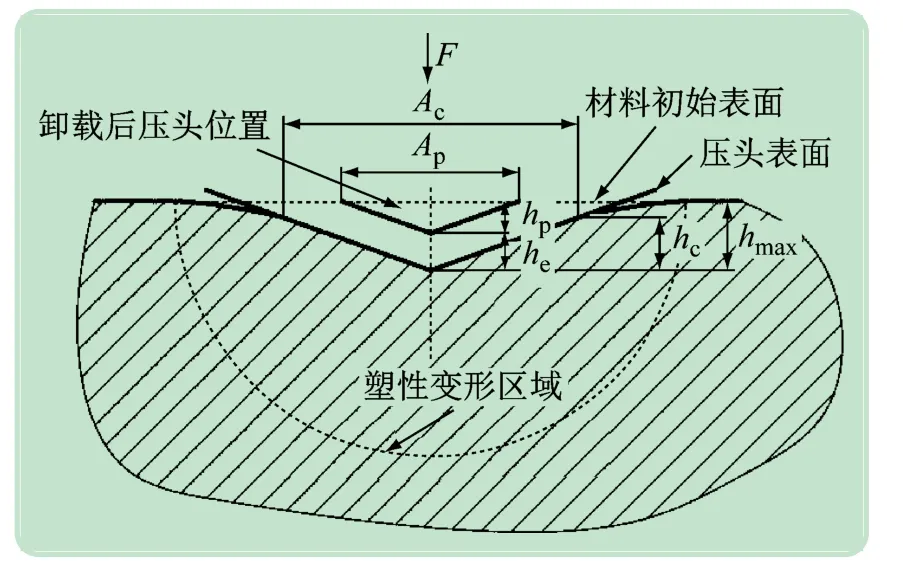
图3 纳米压痕加载/卸载过程变形示意图
对于韧性材料,测试过程中压头下方产生塑性变形,塑性变形功是压头做功积累的结果。故认为材料的临界断裂能与临界载荷下的压痕功相关。压痕断裂能的本构方程如下[7]:
式中:GIEF为压痕断裂能;p为压头平均接触压力,可以用塑性残余深度hp来表征,
F为与塑性残余深度hp对应的瞬时载荷。将式(2)代入式(1),则可整合为[8]
对于塑性残余投影面积Ap的计算,为了考虑“堆积”或“沉陷”现象引起的投影面积偏差,引入径向位移校正因子γ,表达式为
纳米压痕载荷F与hp之间的关系可用二次多项式来表征[9],
式中,C1、C2、C3为常数,可通过拟合纳米压痕载荷与塑性残余深度的关系求得。因此,将式(5)代入式(3),GIEF用hp表示为
对于使用Berkovich压头的纳米压痕测试,材料的弹性模量E可通过下式来表征[9,11]:
式中:Er、ν、Ei、νi和S分别为材料缩减弹性模量、泊松比、压头的弹性模量、泊松比和载荷-位移曲线中的卸载斜率(卸载刚度);β是由于Berkovich压头缺乏轴向对称性而取用的校正因子;φ 为常数,对于Berkovich压头或具有相同横截面积的锥形压头,φ =0.72。
实验过程中临界压痕深度很难直接测量。Lee等[12]发现,随着压痕深度的增加,材料在受损情况下,弹性模量会逐渐降低,且压痕深度与弹性模量之间存在一定的关系。因此,在临界压痕深度处会有一个临界弹性模量。Kachanov[13]提出了损伤变量ω,可以表示为
式中,f为材料的孔洞体积百分率。基于式(12),材料在不同压痕深度下的弹性模量为[14]:
式中:ED为不同压痕深度对应的弹性模量;E0为无损伤条件下的弹性模量。临界孔隙率fc是表征材料临界压痕深度和断裂韧性的重要参数。fc与GTN 塑性损伤模型[15]中的裂缝孔隙率fF相同,基于此关系,可确定裂纹发生时的临界损伤值,进而可根据式(13)求得临界损伤对应的弹性模量。再根据压痕深度与弹性模量的关系,由临界弹性模量E*确定临界塑性深度,最终通过式(7)确定材料的断裂韧性。
1.3 测试方案
纳米压痕测试过程中,加载方式为单点连续加卸载法(压入实验循环加卸载次数为5 次)。以500 mN为例,等比例加载25,50,100,250 和500 mN,在达到每一段目标载荷以后完全卸载,卸载完成后直接在该点处进行下一周期的加载,到达下一目标载荷值之后,重复上述过程至最后一个周期完成。单点连续加卸载法能使压头在同一点连续加卸载,更便捷地获取材料深度与载荷之间的关系,能大大降低实验的复杂程度。为了探索纳米压痕测试过程中的影响因素,采用控制变量法,实验方案如下:
(1)保持最大压入载荷为500 mN,测试3 种不同加载速率(10、20 和40 mN/s)对断裂韧性测试值的影响。
(2)保持压入速率为40 mN/s,测试3 种不同最大压入载荷(300、400 和500 mN)对断裂韧性测试值的影响。
实验获取的数据导入Origin 软件进行绘图,获得加载点处的载荷-位移曲线。通过对加卸载曲线进行处理,获得对应深度下的弹性模量,并记录对应深度下的塑性深度。
2 断裂韧性纳米压痕形貌观测及测试仿真平台
对纳米压痕测试后的试样利用原子力显微镜进行压痕形貌观测,获取卸载后压头区域的变形形貌,原子力显微镜的型号为CSPM5500。
利用有限元软件ABAQUS 对压痕测试过程进行模拟,再现整个过程中的变形行为。
2.1 被压材料与压头几何模型建立
压痕实验过程中,被测材料的尺寸远大于压头尺寸,若按照实际实验试样尺寸建立有限元模型将导致过大的计算量。考虑到实验中被压材料的力学响应都集中在压头附近,在压头远处应力和应变都趋向于零,根据圣维南原理可以适当缩小材料径向的尺寸,在厚度方向上,Partheepan 等[16]指出试样的高度至少应达到最大压痕深度的10 倍。因此,本文采用10 μm×10 μm×6 μm的立方体模型。
压头压入过程中,一共有两种材料模型,实验材料与压头材料。实验过程中采用的Berkovich 压头材质为金刚石,弹性模量为1 141 GPa,泊松比为0.007;实验材料为X80 管线钢。有限元模拟过程中,由于金刚石压头的弹性模量比管线钢的弹性模量高出一个数量级,为提高计算效率,在有限元模型中压头采用解析刚体建模。
为防止材料模型局部边缘对实验结果的影响,在试样最外围1 周采用无限大三维单元(CIN3D8),其他部分采用8 节点线性减缩积分单元(C3D8R)。为减少计算量同时保证计算精度,从接触中心向外边缘网格尺寸逐渐增大。试样网格划分剖面图如图4 所示,划分为4 个区域:①中心接触区;②接触影响区;③塑性影响区;④无限大弹性边界。在压头下方区域最小网格尺寸为40 nm ×40 nm ×40 nm,整个模型共计403 142 个单元,421 824 个节点。为了避免分析过程中产生沙漏现象使单元刚度降低,本文采用Enhause沙漏控制方式。

图4 试样剖面网格示意图
2.2 有限元分析边界条件
有限元分析中施加的边界条件如图5 所示。试样底面在实验测试过程中固定于实验台,故试样底部所有节点6 个方向的自由度均限制为零,压头只有在高度方向,即Z方向上自由移动,因此压头除Z方向以外,其余5 个自由度也均为零。

图5 有限元分析边界条件
当压头压入试样,材料在压头下方应力的作用下发生弹塑性变形。弹性区约束塑性区材料沿加载方向的流动,导致压痕凹坑边缘产生“堆积”或“沉陷”现象,这些现象将对弹性模量的计算产生不利影响。为探究材料表面产生的“堆积”或“沉陷”现象,需提取压痕表面形貌。由于ABAQUS 后处理模块无法直接获得压痕表面形貌图,本文根据ABAQUS中计算的ODB文件,利用Python 脚本提取压痕表面网格的坐标信息,并利用Origin绘制三维形貌图,提取程序的流程如图6 所示。

图6 压痕表面三维形貌数据提取程序流程图
2.3 本构模型
有限元仿真过程中采用的本构模型如下式所示:总应变ε总可分为弹性应变εe和塑性应变εp。
弹性应变εe通过胡克定律进行计算。对于塑性应变εp,为了表征塑性变形过程中产生的损伤,本文采用GTN模型[15]对塑性应变进行计算:
式中:φ 为塑性屈服函数;σe为von-Mises 应力;σs为材料的屈服强度;σm为静水应力;f*为即时空洞体积分数;f为空洞体积分数;q1、q2为修正因子,q3=;fF为材料完全失去承载能力时的孔洞率;fc为空洞开始聚集的临界值;fN为形核二项粒子体积分数;εN为孔洞形核的平均应变;SN为形核应变的标准差;为塑性静水应变。
无损状态下X80 管线钢的弹性模量为206 GPa,σs=594 MPa,泊松比为0.3。GTN模型中q1=1.5,q2=1.0,q3=2.25,εN=0.3,SN=0.1,fN=0.003,f0=1.87×10-4,fc=0.02,fF=0.15[11]。
3 实验结果及分析
3.1 纳米压痕实验测试
3.1.1 不同压痕速率下的断裂韧性计算
由制定的实验方案,采用应力控制法对加载点进行5 次加载和卸载。不同加载速率10、20 和40 mN/s下对应的加载点载荷-位移关系如图7 所示。从图中可以看出,相同最大载荷下,加载点位移随加载速率的增加而增加。对于10 mN/s的压痕速率,5 个加载-卸载循环对应的塑性深度分别为184.8、248.8、412.7、705.2 和1 231.1 nm。对于20 mN/s 的压痕加载速率,5 个加载-卸载循环对应的塑性深度分别是210.7、300.2、519.8、846.4 和1 416.2 nm。对于40 mN/s的压痕速率,5 个加载-卸载循环对应的塑性深度分别是440.9、636.85、1 033.3、1 399.8 和2 112.8 nm。

图7 单点连续加卸载下不同加载速率的载荷-位移曲线
基于式(5)和图7 中的数据,建立压痕载荷F与残余塑性深度hp的关系,通过数据拟合可得到10、20、40 mN/s 3 种状态下的表达式分别为:
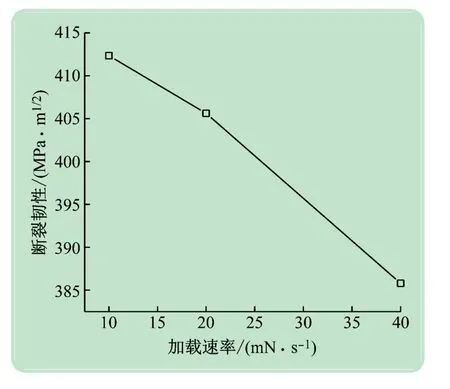
图8 不同加载速率下断裂韧性测试值变化
3.1.2 不同最大压入载荷下的断裂韧性计算
对于不同最大压入载荷下的断裂韧性测试与计算,与不同加载速率下的测试情况相似。采用单点连续卸载法,在达到每一段目标载荷以后完全卸载,卸载完成后直接在该点处进行下一周期的加载,到达下一目标载荷值之后,重复上述过程至最后一个周期完成。压头加载速率为40 mN/s,最大载荷分别设置300、400和500 mN 3 种。3 组数据对应的加载点载荷-位移关系如图9 所示。由图可见,由于加载速率相同,其加载和卸载斜率都很接近。最大载荷为300 mN时,5 个加载-卸载循环对应的塑性深度分别是394.01、898.48、1 220.36、1 454.8 和1 671.8 nm;最大载荷为400 mN时,5 个加载-卸载循环对应的塑性深度分别是451.9、630.2、974.14、1 438.7 和1 983.3 nm;最大载荷为500 mN时,5 个加载-卸载循环对应的塑性深度分别是625.83、791.05、1 177.98、1 683.23 和2 252.1 nm。

图9 单点连续加卸载下不同最大载荷的载荷-位移曲线
基于式(5)和图9 中的数据,通过数据拟合可得到最大压入载荷300、400、500 mN 3 种状态下F与残余塑性深度hP的表达式分别为:
根据式(5)~(7)、(21)~(23),可获得不同压入速率下对应的断裂韧性测试值KJC,如图10 所示。由图可见,在压入速率不变的前提下,随着最大压入载荷的增大,断裂韧性测试值KJC随之变小。
综上所述,最大压入载荷不变时,随着加载速率的增加,断裂韧性测试值变小;加载速率不变时,随着最大压入载荷的增加,断裂韧性测试值逐渐变小。该规律对于后续其他压痕实验研究及参数的选取具有较好的指导意义。
3.2 压痕形貌
图11 所示为在原子力显微镜下观测的纳米压痕三角形凹坑和压痕边缘的凸起现象。郭永泽[17]在对不同材料堆积现象的研究中指出,材料表面的堆积程度与硬化指数有关。硬化指数越小,材料表面堆积越显著。本文采用的X80 管线钢的硬化系数小于0.2,

图11 X80管线钢压痕形貌图
因此材料表面的堆积效应比较显著,实验结果与理论分析一致。由图可见,接触边缘处堆积现象明显,最大堆积高度可达到115 nm左右,堆积高度的存在会严重影响压入深度、塑性投影面积等参数的测试与计算,进而进一步说明了考虑压痕形貌“堆积”或“沉陷”现象对弹性模量进行修正的必要性。
3.3 有限元仿真
利用原子力显微镜进行压痕形貌观测可以直观地显示压头附近区域的变形情况,但对于测试中的过程量难以直接观测。有限元仿真可以再现整个过程中的压痕形貌变化。为了更直观地观测压痕表面的堆积现象,采用编写的后处理程序提取材料表面网格变形信息,绘制深度方向的等高线图,获得压痕表面堆积图。图12 所示为最大压痕深度400 nm下压头在不同阶段卸载后的形貌图。在压头边缘沿着压头投影的棱边方向,有明显的材料堆积现象,且堆积程度沿着棱边中心向两侧逐渐减小。随着压痕深度的增加,表面的堆积形貌高度逐渐增加,压痕深度为100 nm 时,表面的最大堆积高度为35 nm。当压痕深度分别为200 nm 和400 nm时,压痕表面的最大堆积高度分别为73 nm和106 nm左右。其中压痕深度为400 nm时有限元仿真获得堆积高度与图11 中利用原子力显微镜获得的数据吻合性较好,进而验证了本文建立的有限元仿真方法的可行性,利用有限元的方法能够精确获得压痕的表面形貌。
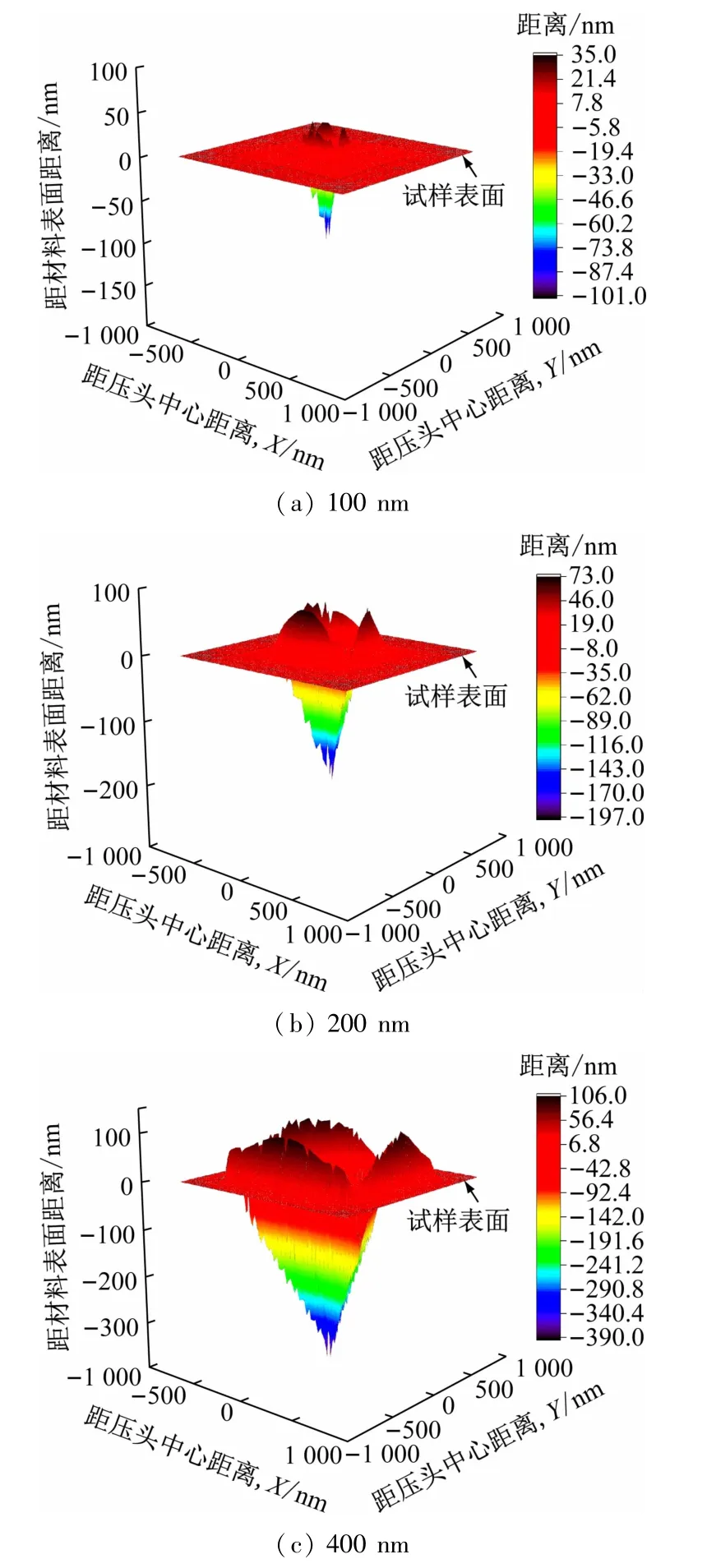
图12 不同压入深度时压痕表面形貌三维等高线
4 结 语
本文结合科研项目研究,通过综合性实验设计,发展了基于小试样的断裂韧性纳米压痕测试方法,探清了压入速率和压入深度对X80 管线钢断裂行为的影响规律,掌握了压痕测试过程中压痕形貌的变化过程。最大压入载荷不变时,随着压入速率的提升,残余塑性深度值变大,断裂韧性测试值逐渐变小;压入速率不变时,随着最大压入载荷的提升,残余塑性深度值变大,断裂韧性测试值逐渐变小。
通过该综合性实验的开展,使学生能够从文献查阅、公式推导、实验操作、数据处理、微观形貌观测、有限元分析及实验报告撰写等过程中完成一次完整的科研体验,锻炼文献检索与阅读能力、逻辑推导能力、微观探知能力及实践动手能力,掌握科学研究的基本思路和方法,培养科研思维能力。同时,有利于推动科研资源与教学资源的有效整合和共享,促进科研与教学相互渗透,形成科教结合协同发展的良好氛围。

